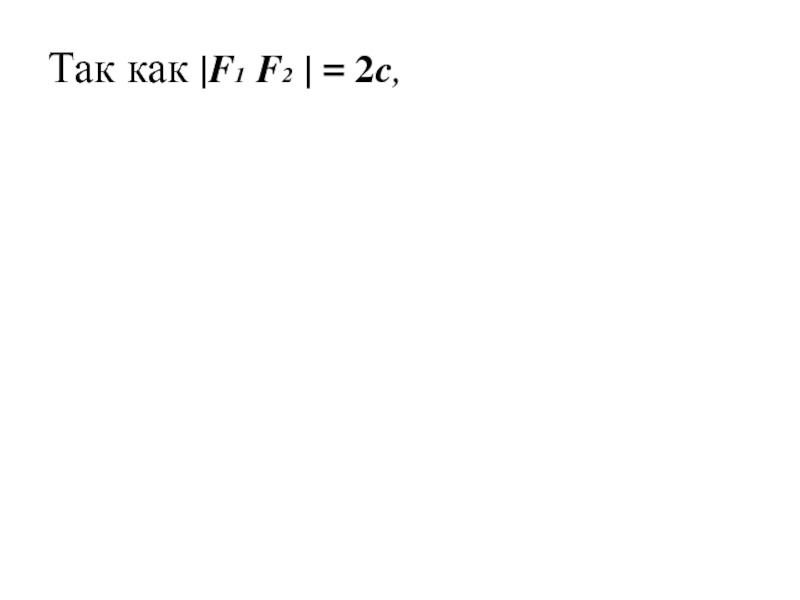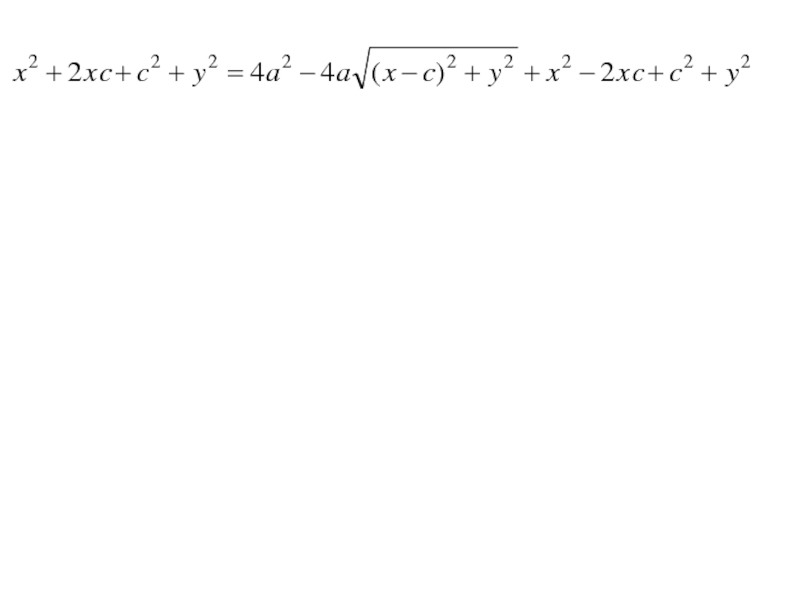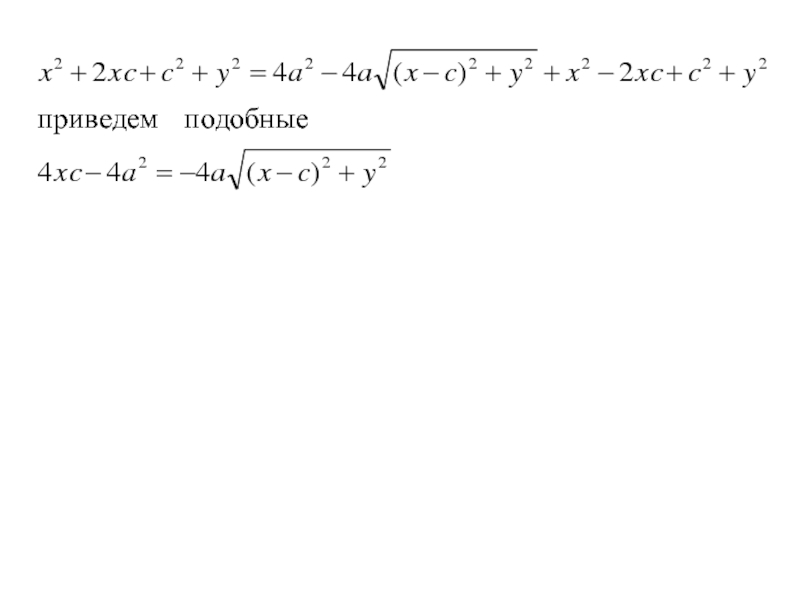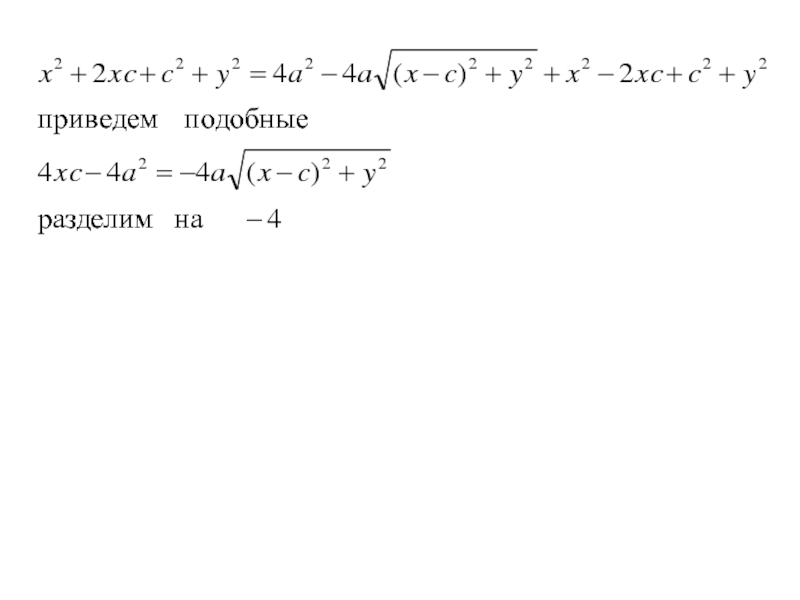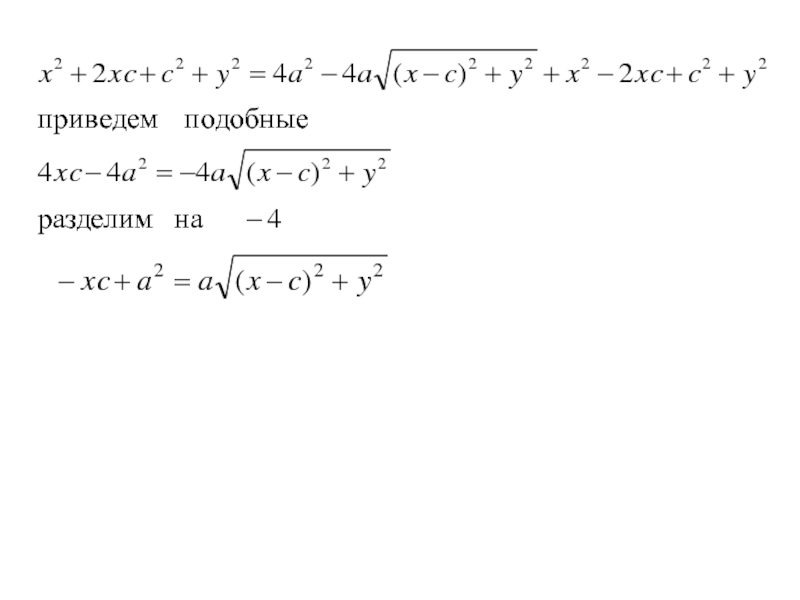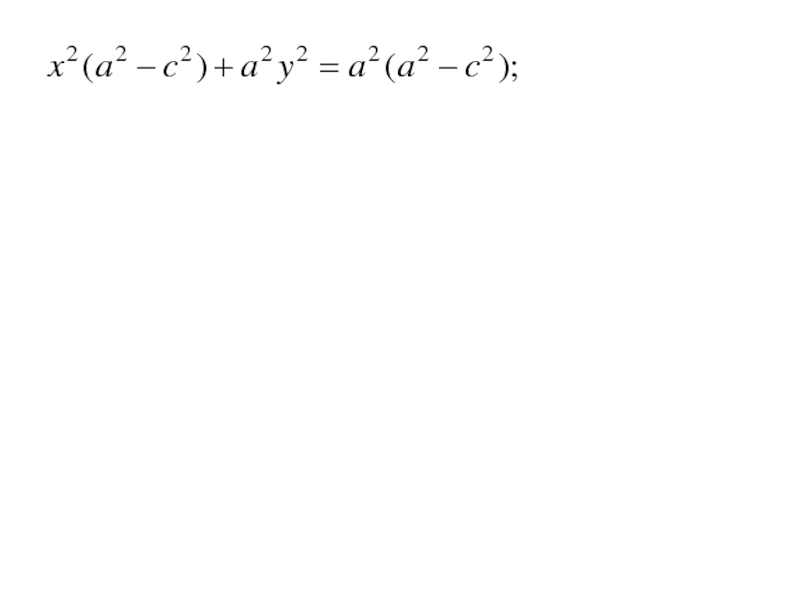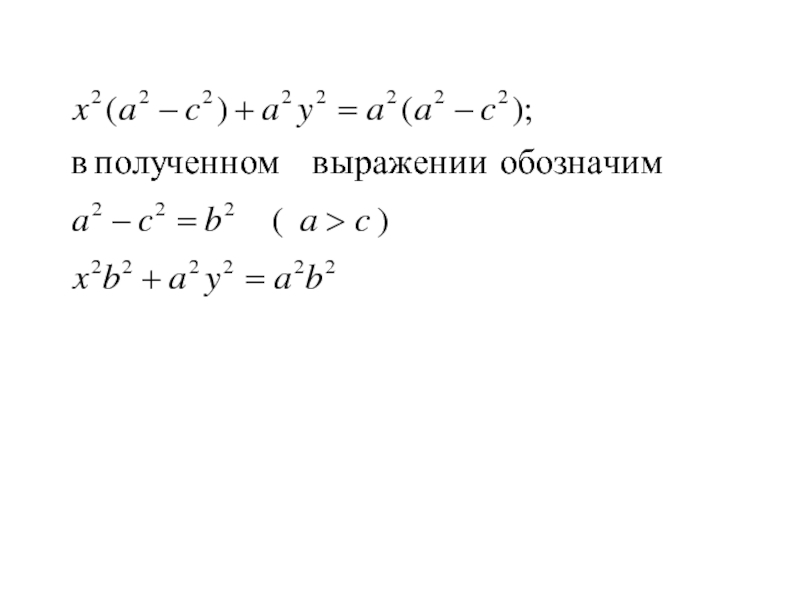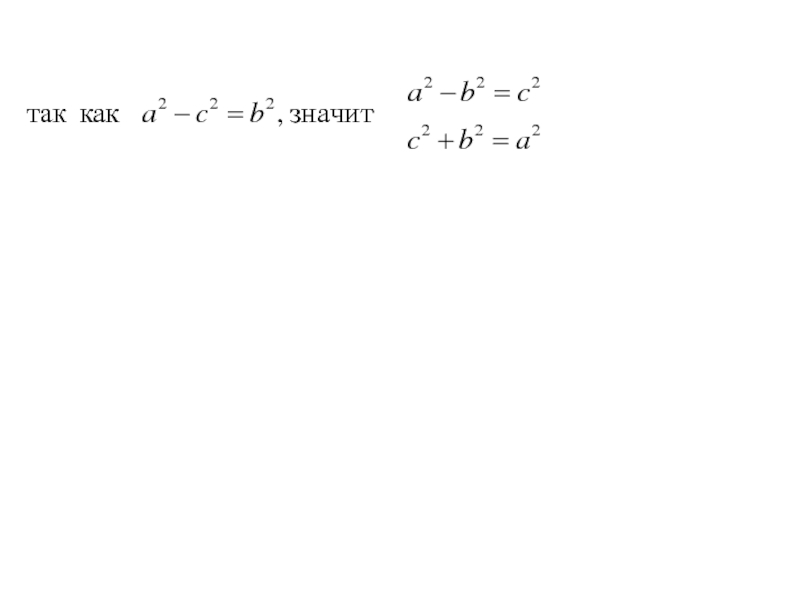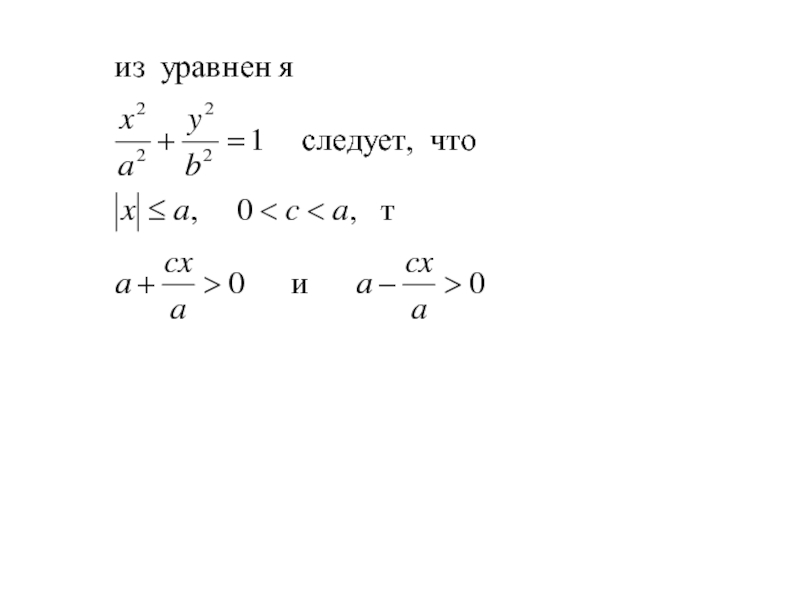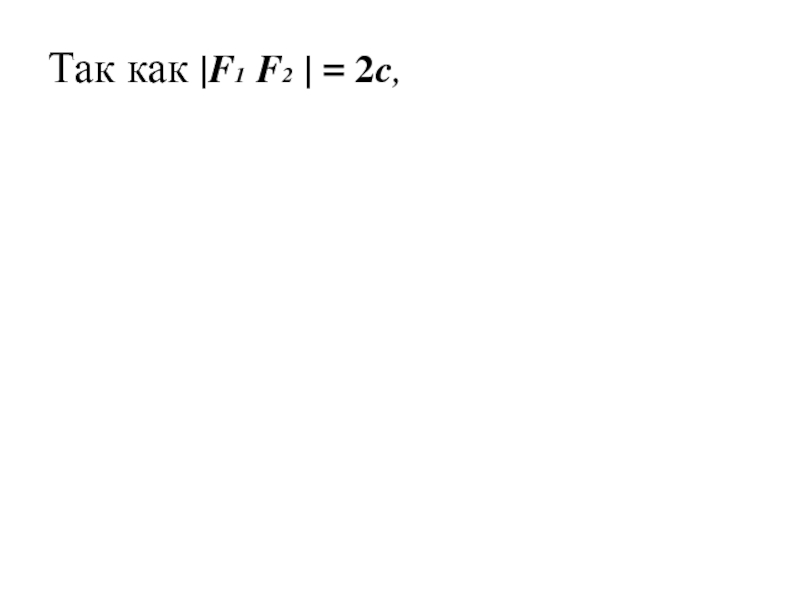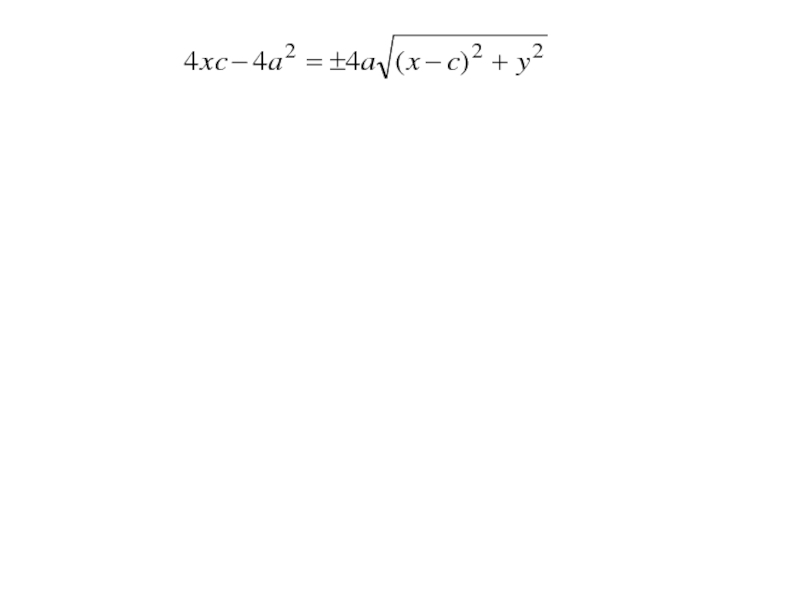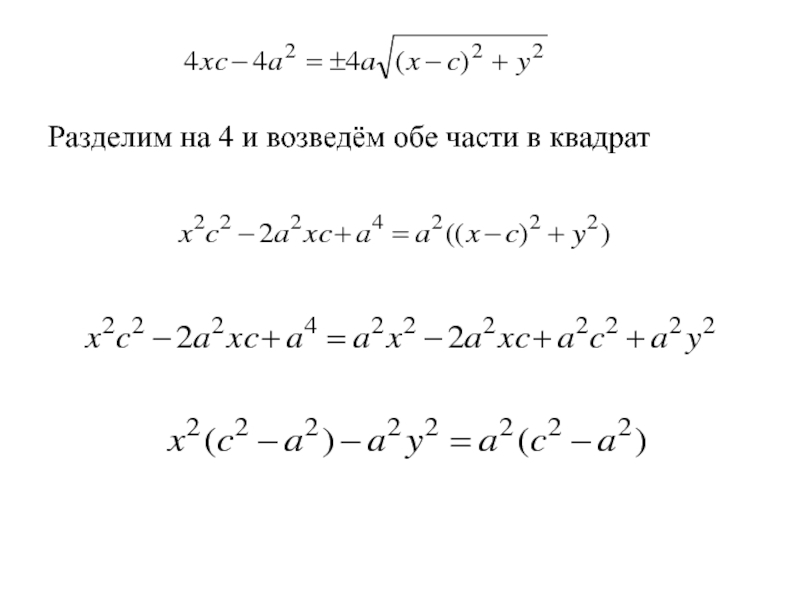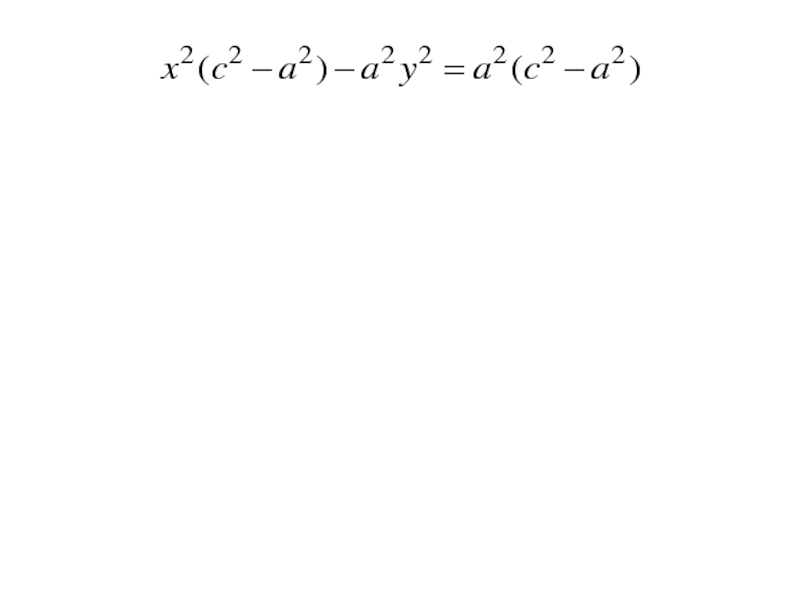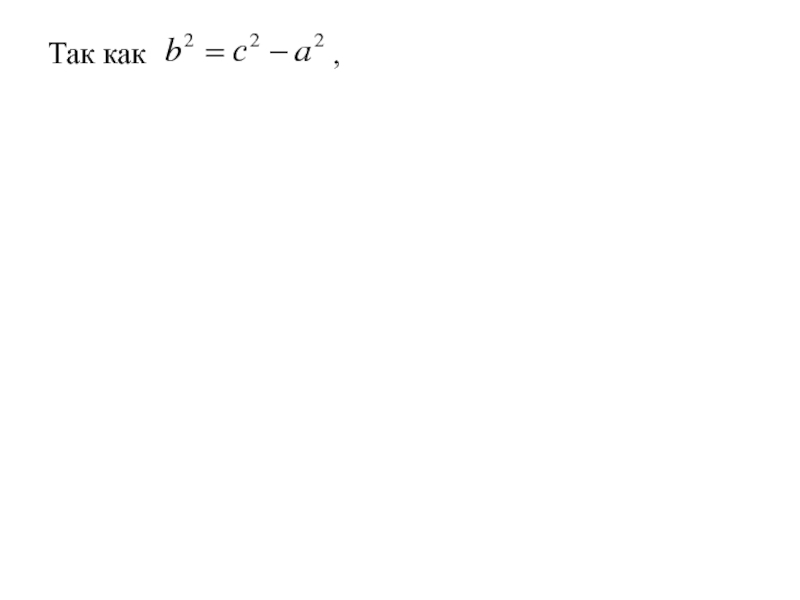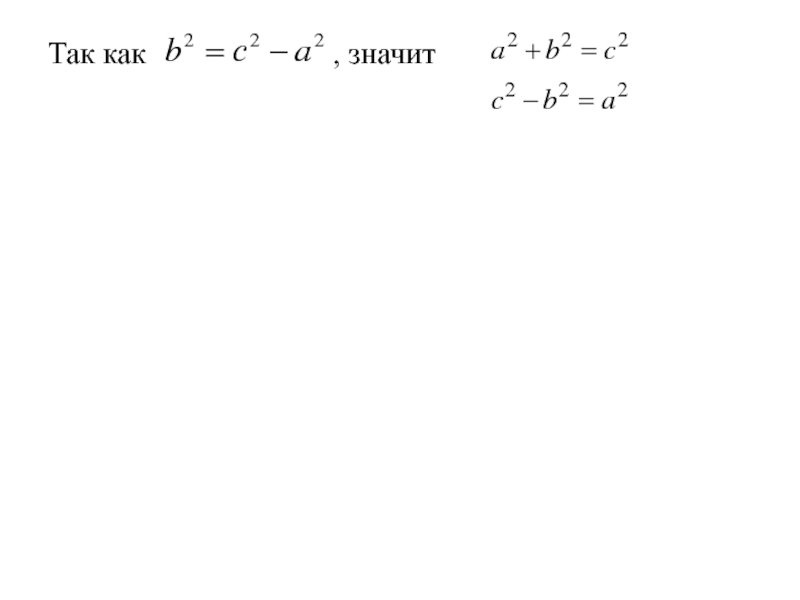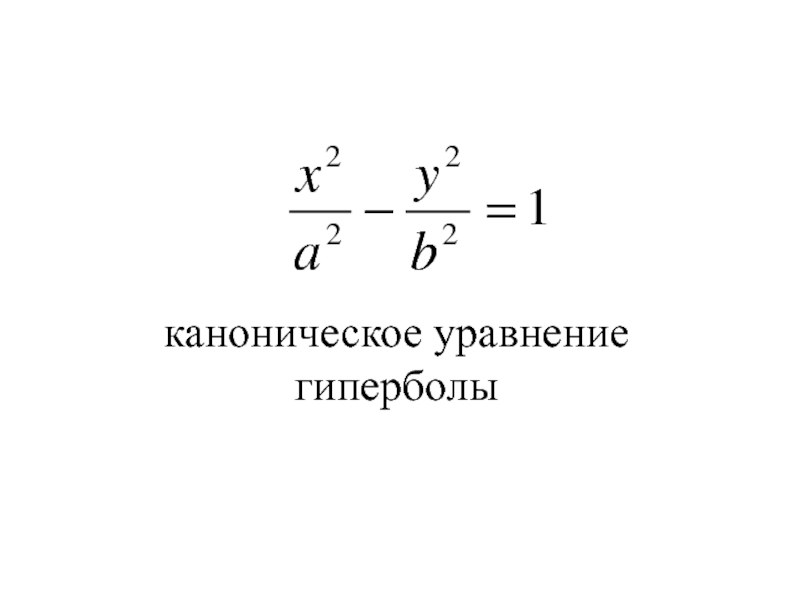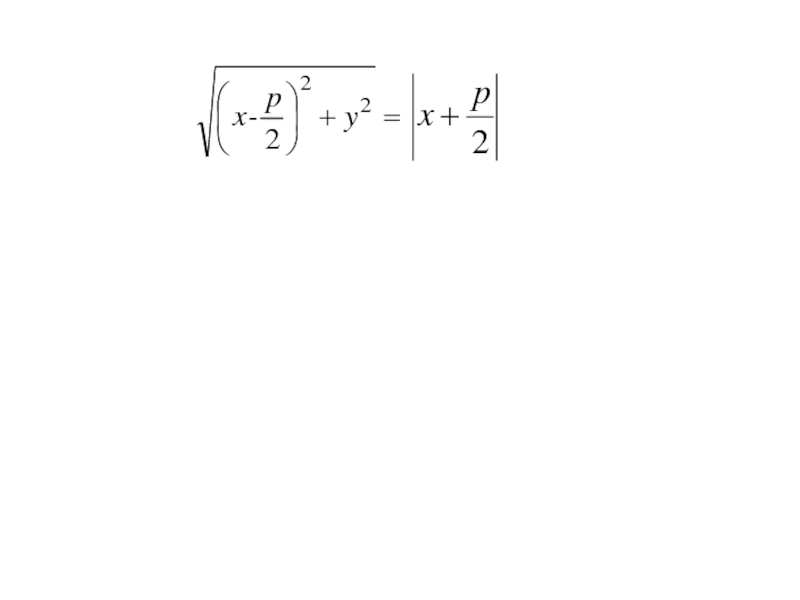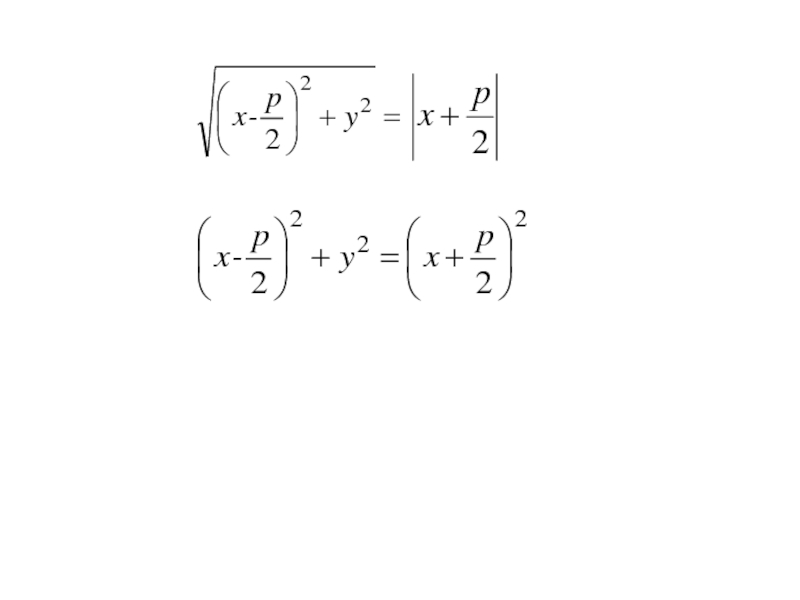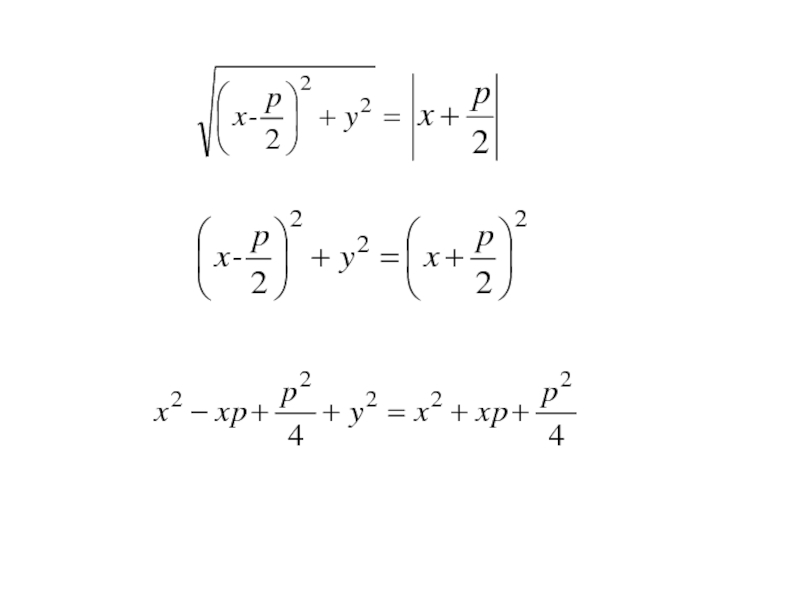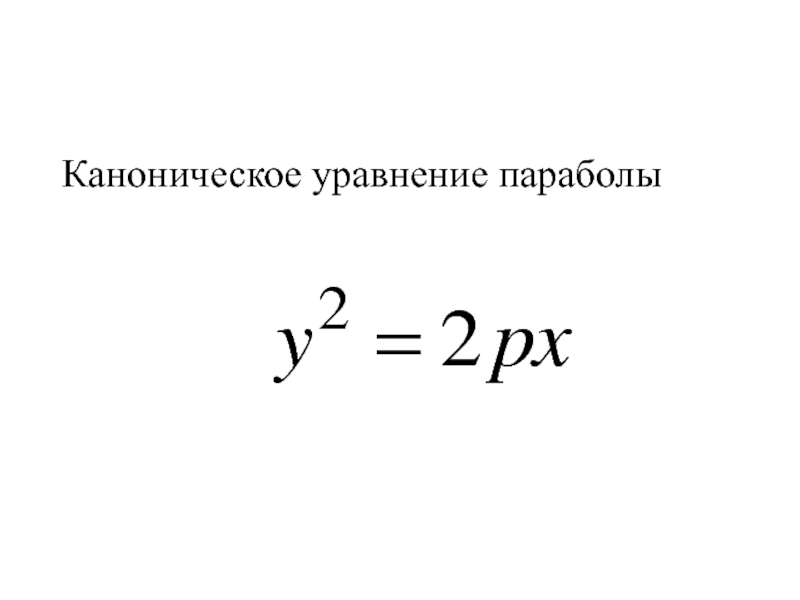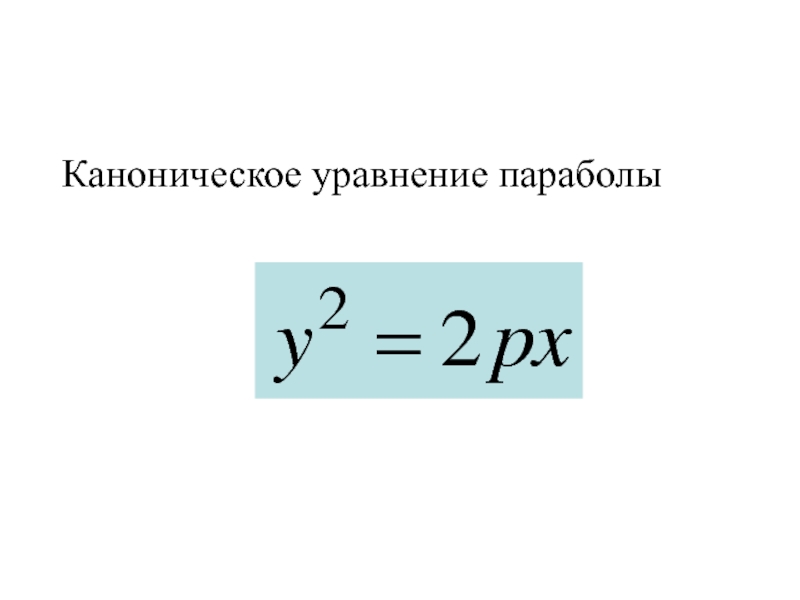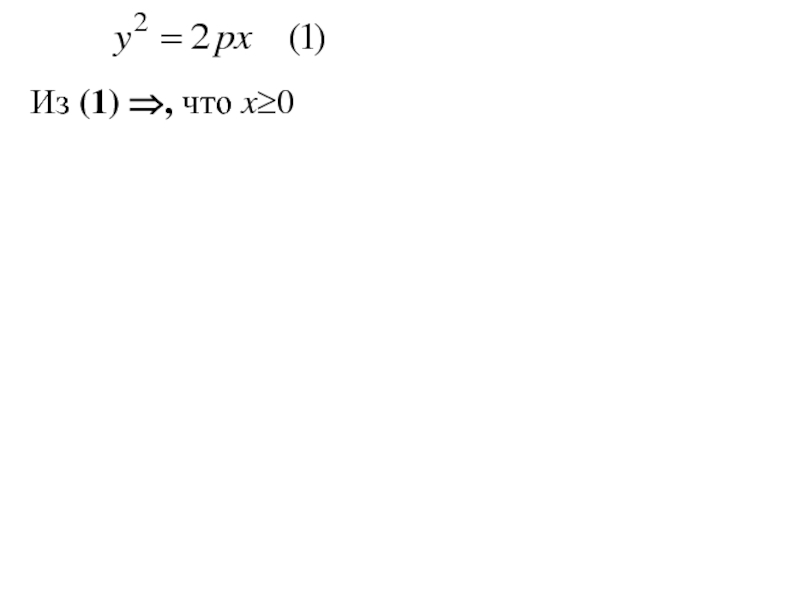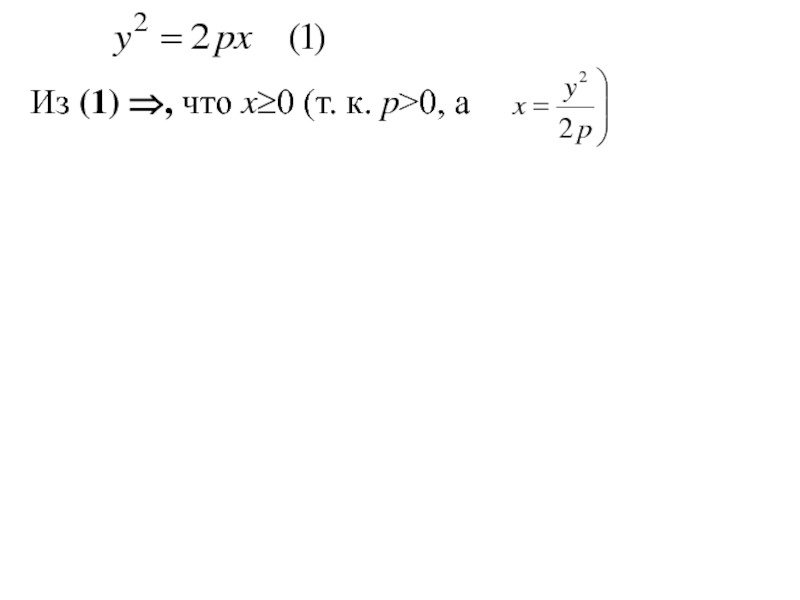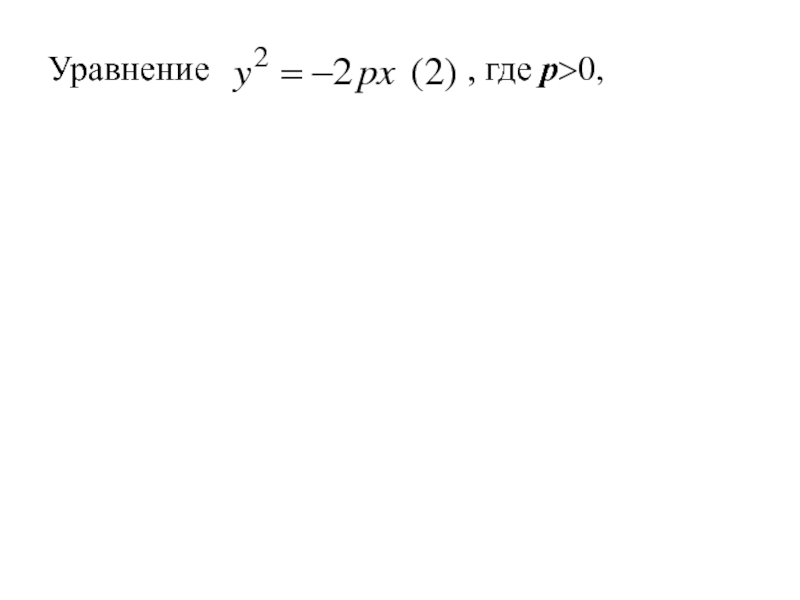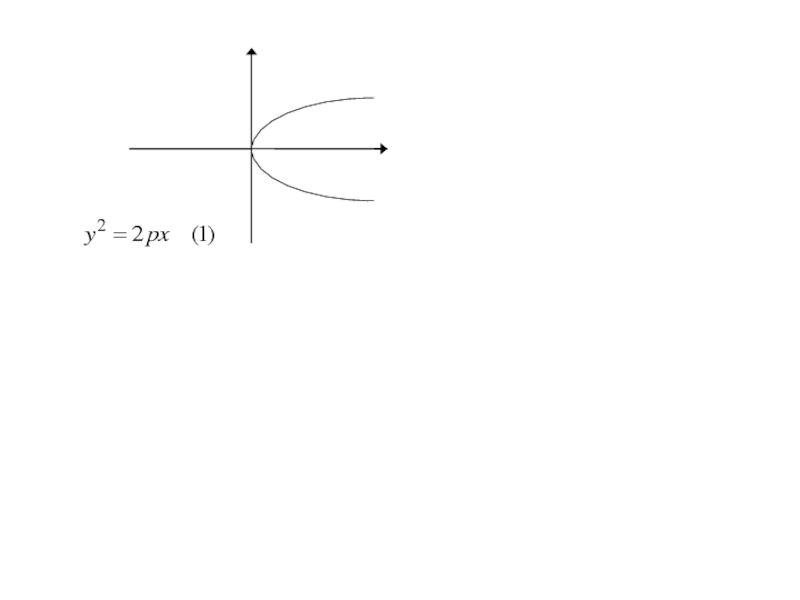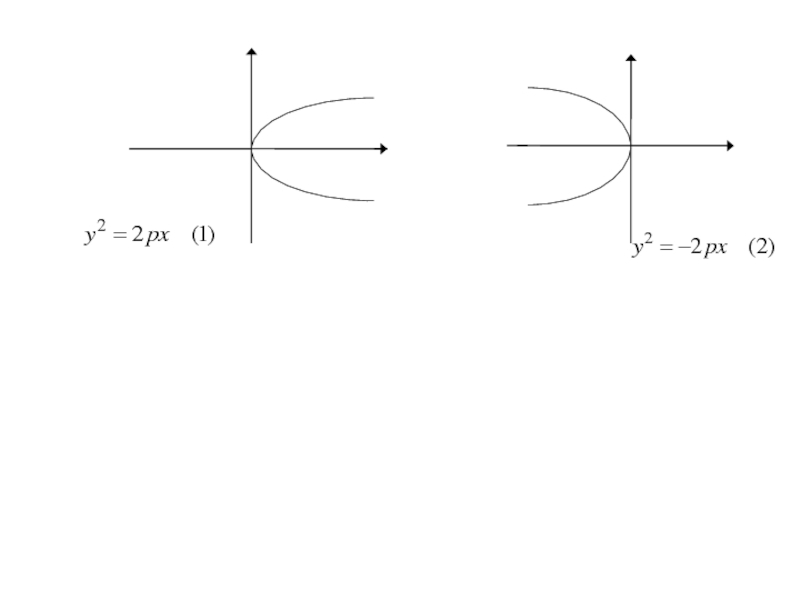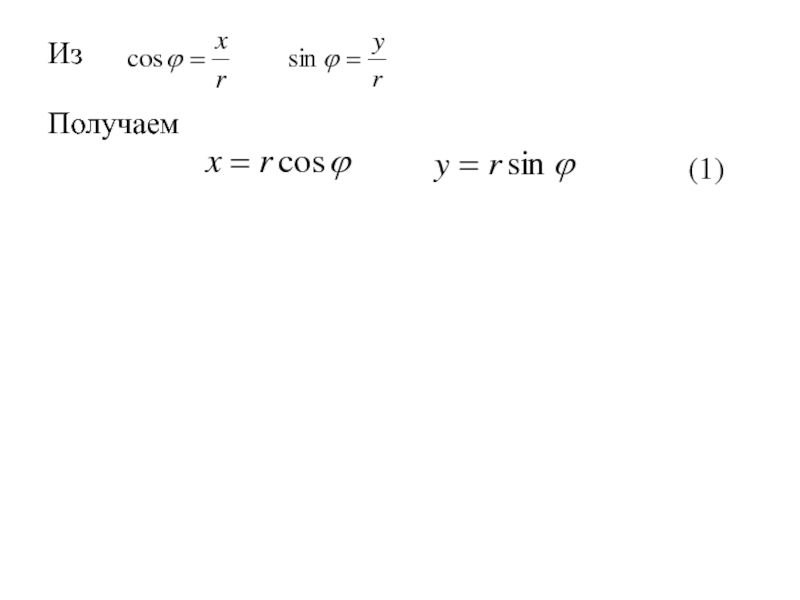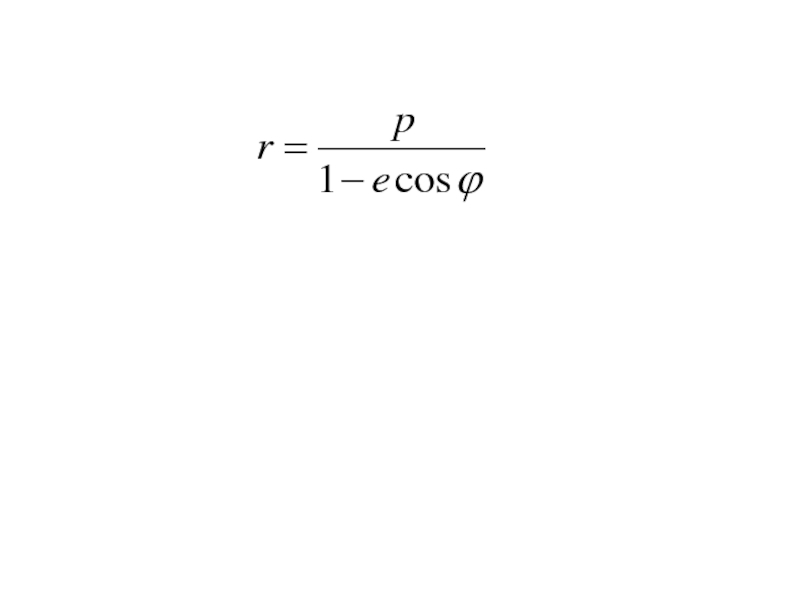Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
канонические уравнения кривых второго порядка
Содержание
- 1. канонические уравнения кривых второго порядка
- 2. Содержание1. Эллипс и его каноническое уравнение. 4.
- 3. Взять в библиотеке методичку:КРИВЫЕ ВТОРОГО ПОРЯДКА:АДАПТИВНО-МОДУЛЬНАЯ ТЕХНОЛОГИЯМетодические рекомендациидля самостоятельной работы студентов
- 4. 1. Эллипс и его каноническое уравнение Эллипсом
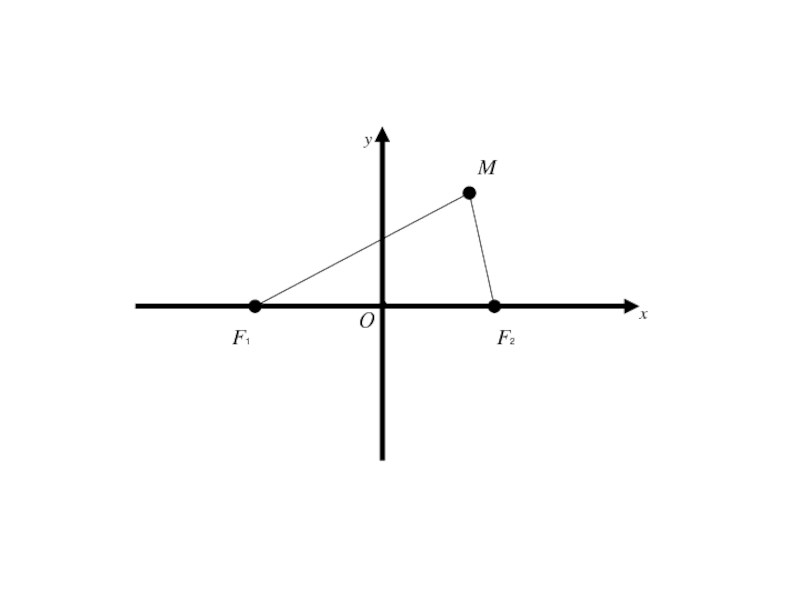
- 5. F1
- 6. F1 F2
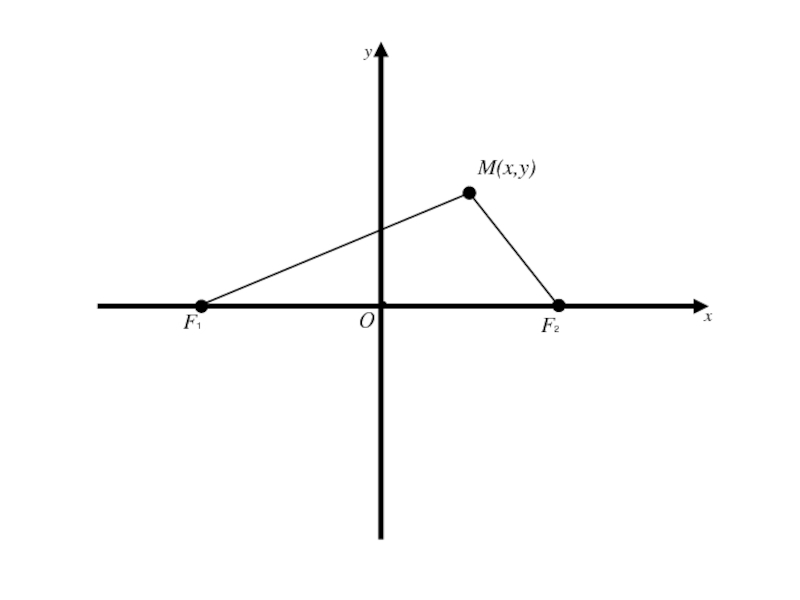
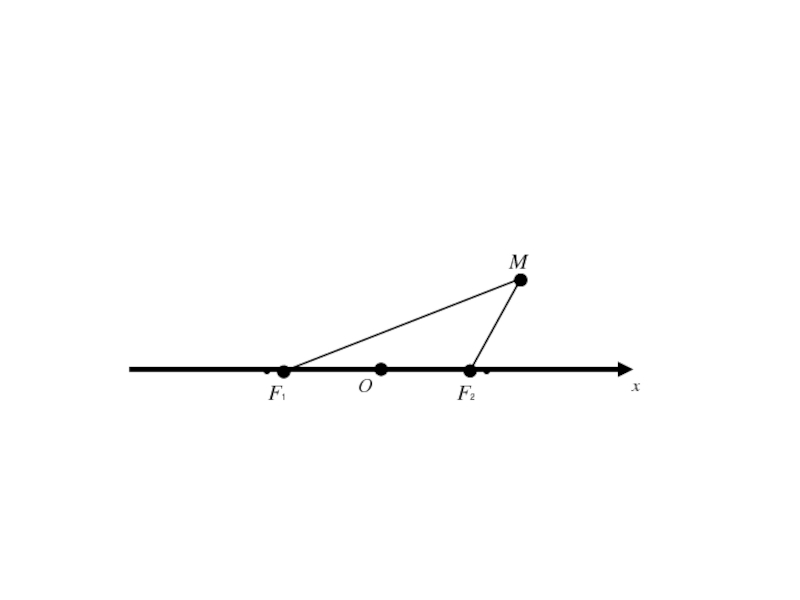
- 7. F1 F2 M
- 8. F1 F2 M
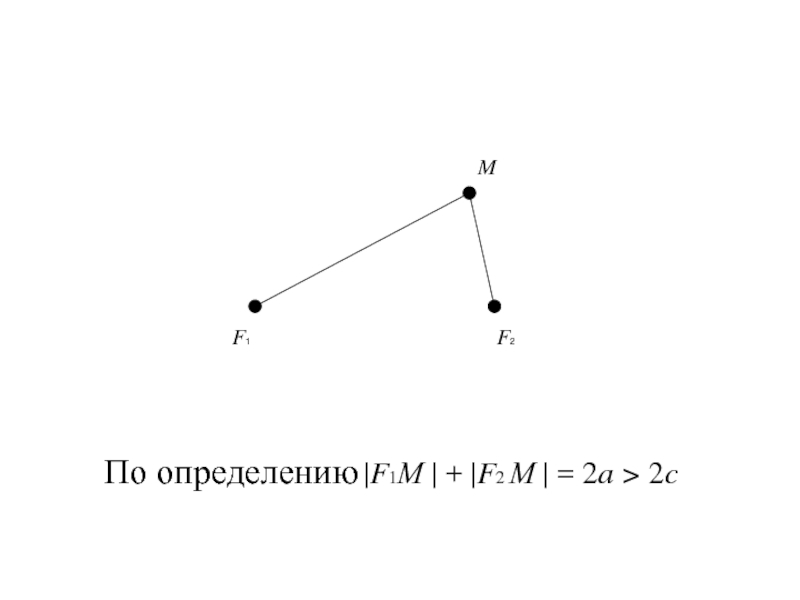
- 9. F1 F2 MПо определению |F1М | + |F2 М | = 2a > 2c
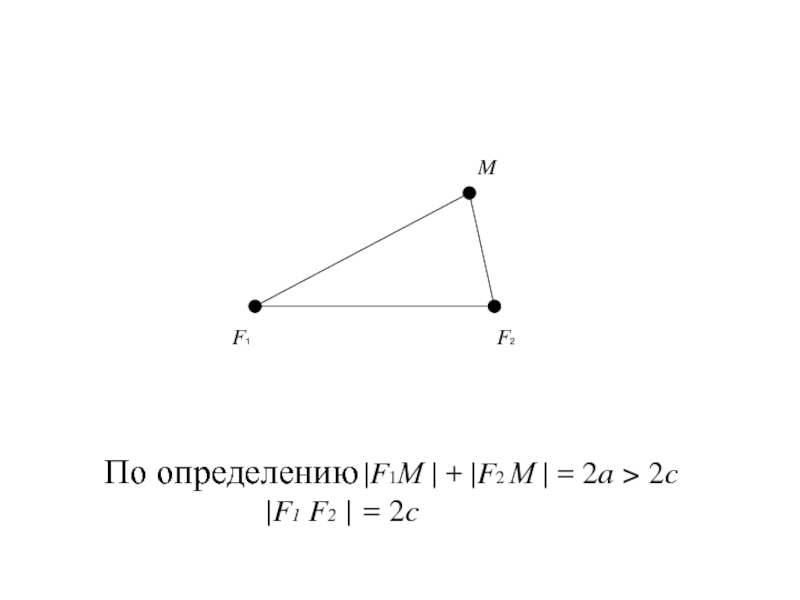
- 10. F1 F2 MПо определению |F1М | +
- 11. F1 F2 M
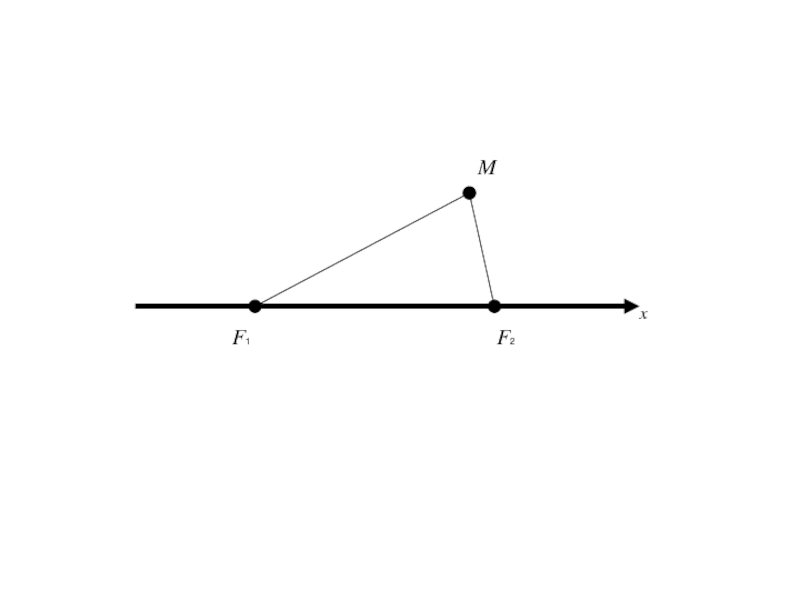
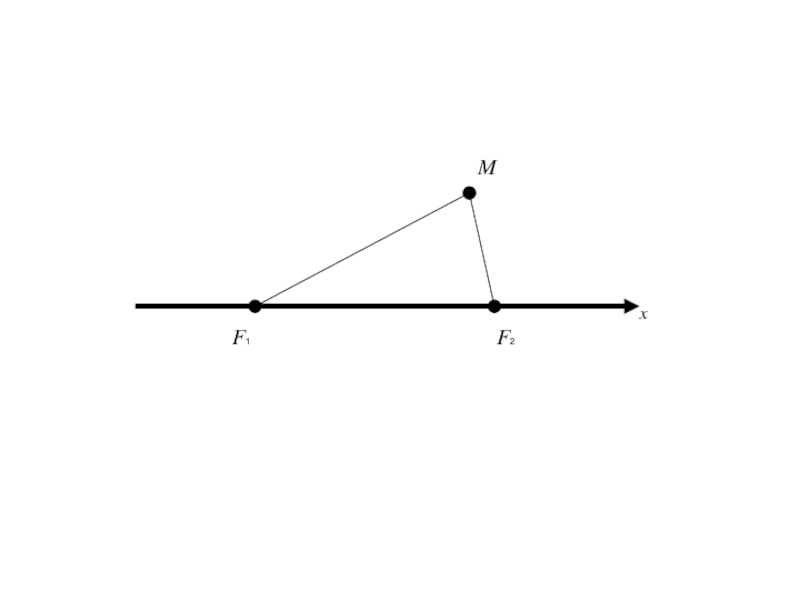
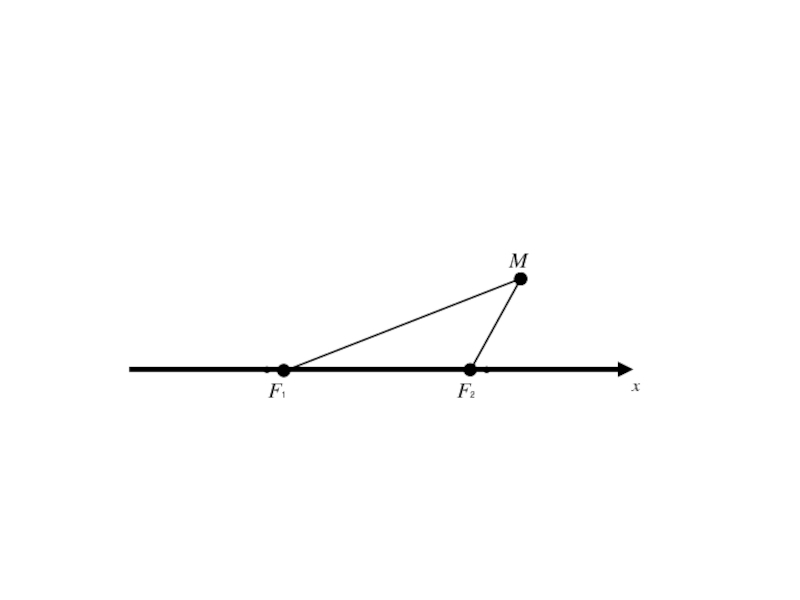
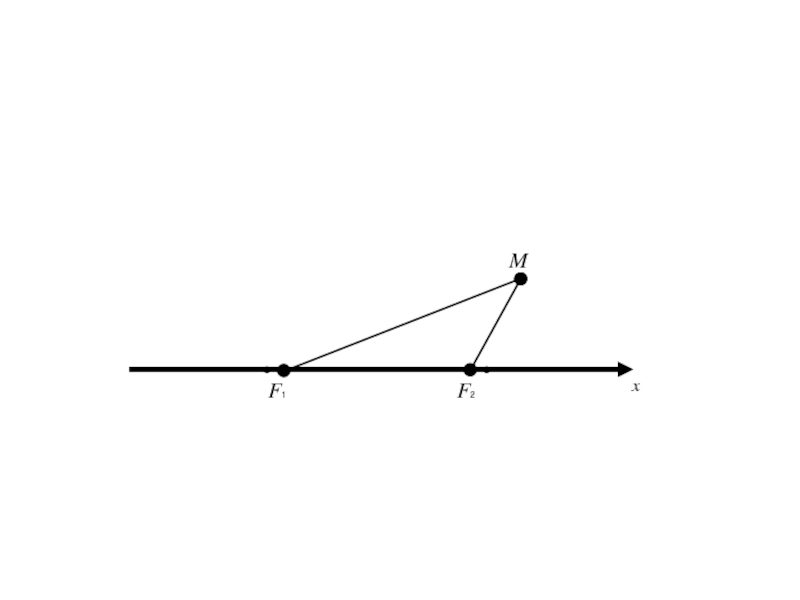
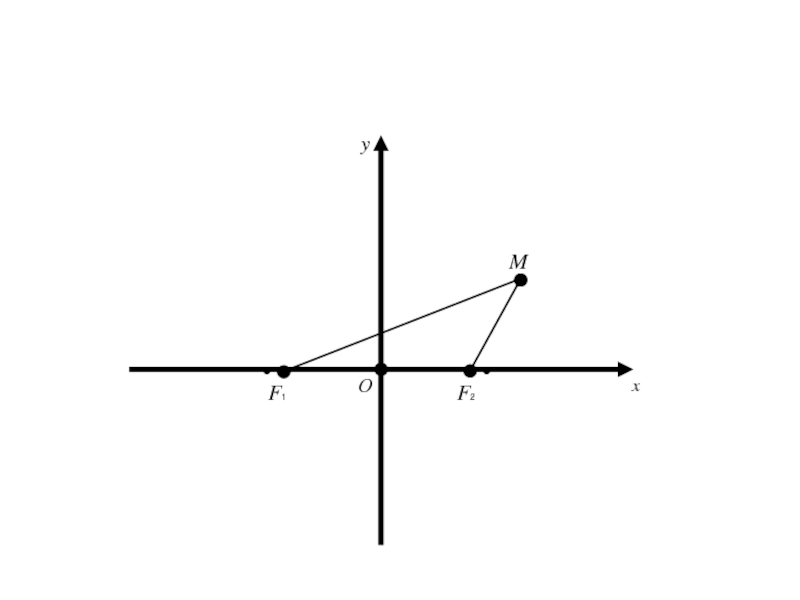
- 12. F1 F2 Mx
- 13. F1 F2 Mx
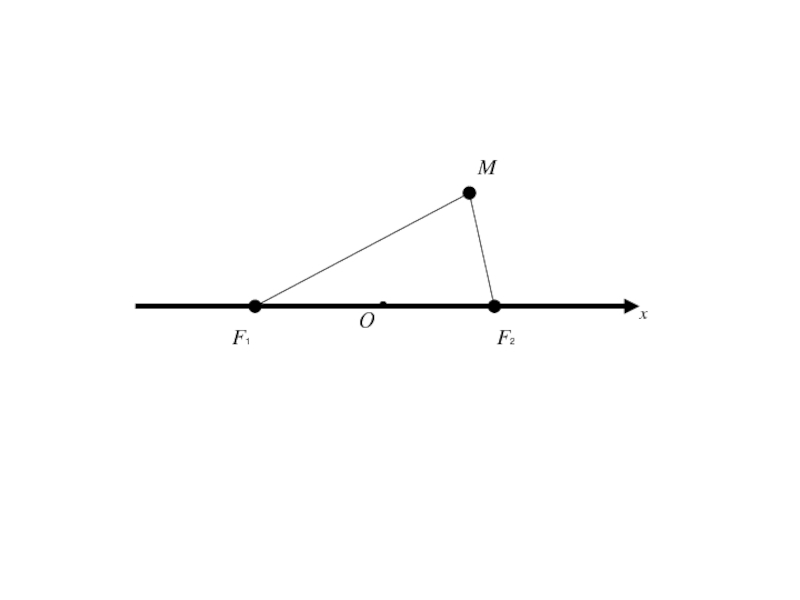
- 14. F1 F2 MОx
- 15. F1 F2 MОxy
- 16. Так как |F1 F2 | = 2c,
- 17. Так как |F1 F2 | = 2c,
- 18. Так как |F1 F2 | = 2c,
- 19. Так как |F1 F2 | = 2c,
- 20. Так как |F1 F2 | = 2c,
- 21. По определению |F1М | + |F2 М | = 2a (1)тогда
- 22. По определению |F1М | + |F2 М | = 2a (1) тогда
- 23. По определению |F1М | + |F2 М | = 2a (1) тогда
- 24. По определению |F1М | + |F2 М | = 2a (1) тогда
- 25. По определению |F1М | + |F2 М | = 2a (1) Получим
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Таким образом, мы доказали, что координаты любой точки M (x; y) эллипса удовлетворяют уравнению (2).
- 38. Таким образом, мы доказали, что координаты любой
- 39. Если числа x и y удовлетворяют уравнению
- 40. Если числа x и y удовлетворяют уравнению
- 41. Докажем это утверждение
- 42. Докажем это утверждениеПусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :
- 43. Докажем это утверждениеПусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :
- 44. Докажем это утверждениеПусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :
- 45. Докажем это утверждениеПусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :
- 46. Докажем это утверждениеПусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Слайд 52
- 53. Слайд 53
- 54. Таким образом, уравнение (2) есть уравнение эллипса,
- 55. Слайд 55
- 56. Слайд 56
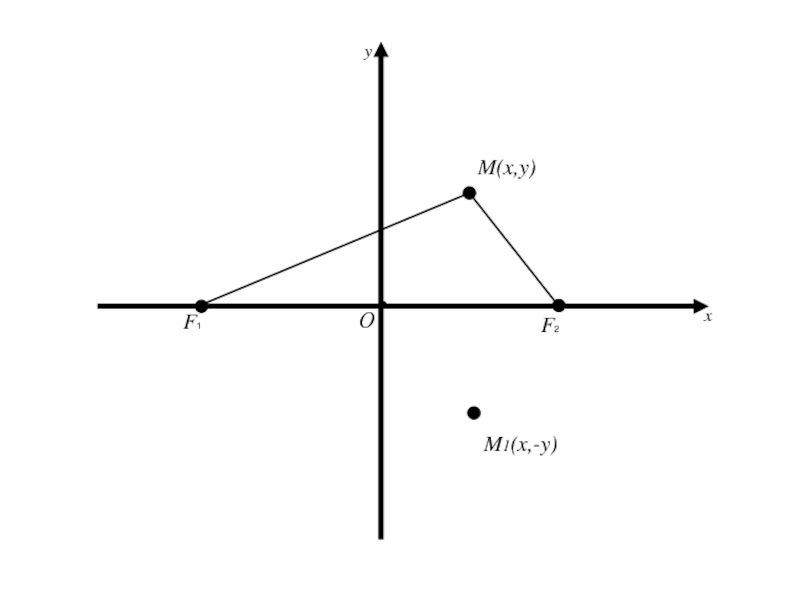
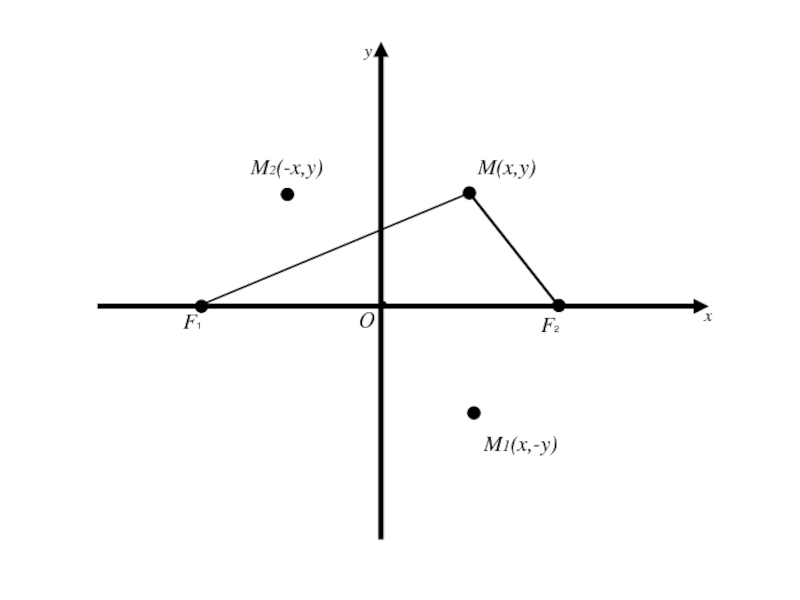
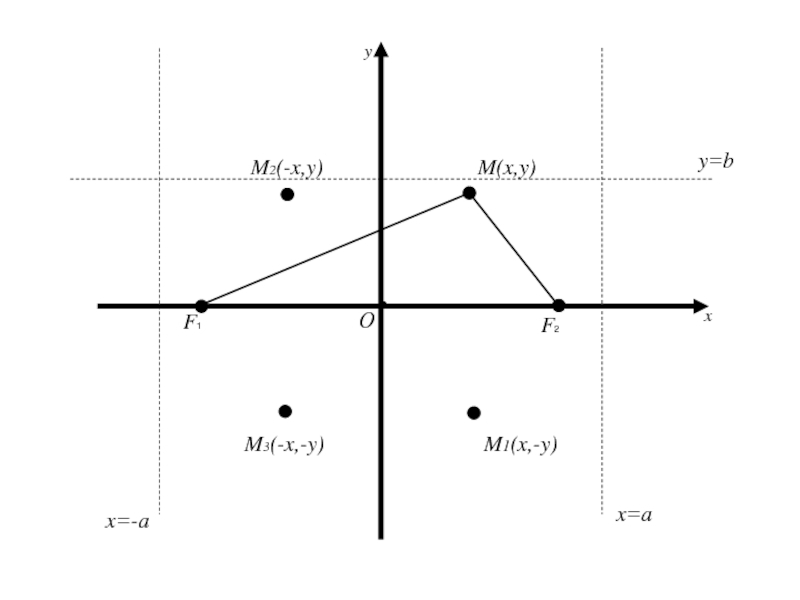
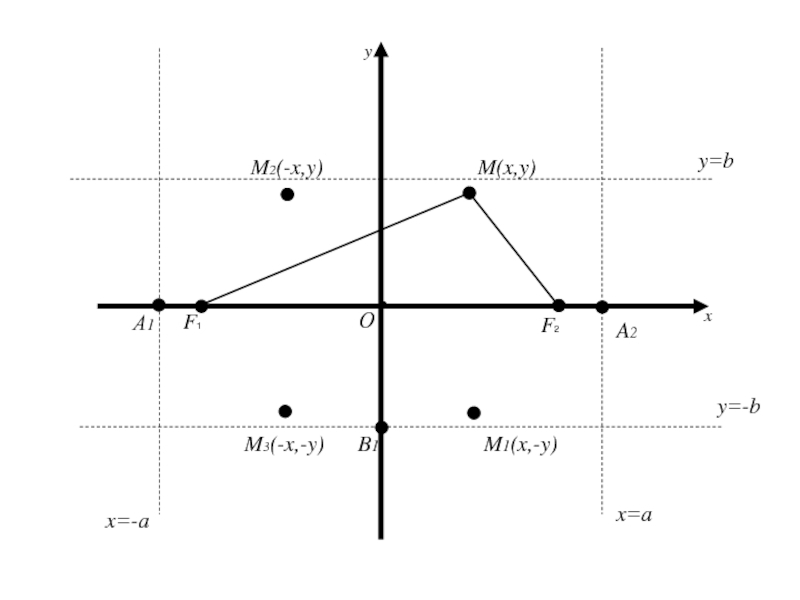
- 57. 2. Исследование формы эллипса. Так как координаты
- 58. 2. Исследование формы эллипса. Так как координаты
- 59. 2. Исследование формы эллипса. Так как координаты
- 60. Следует, что для координат любой точки имеет место
- 61. Следует, что для координат любой точки имеет
- 62. M(x,y)ОxyF2 F1
- 63. M(x,y)ОxyM1(x,-y)F2 F1
- 64. M(x,y)ОxyM2(-x,y)M1(x,-y)F2 F1
- 65. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)F2 F1
- 66. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=aF2 F1
- 67. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-aF2 F1
- 68. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=bF2 F1
- 69. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bF2 F1
- 70. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1F2 F1
- 71. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1A2F2 F1
- 72. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1B1A2F2 F1
- 73. M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1B2B1A2F2 F1
- 74. F2 M(x,y)ОxyM2(-x,y)M3(-x,-y)M1(x,-y)x=ax=-ay=by=-bА1B2B1A2F1
- 75. F2 MОxyА1B2B1A2F1
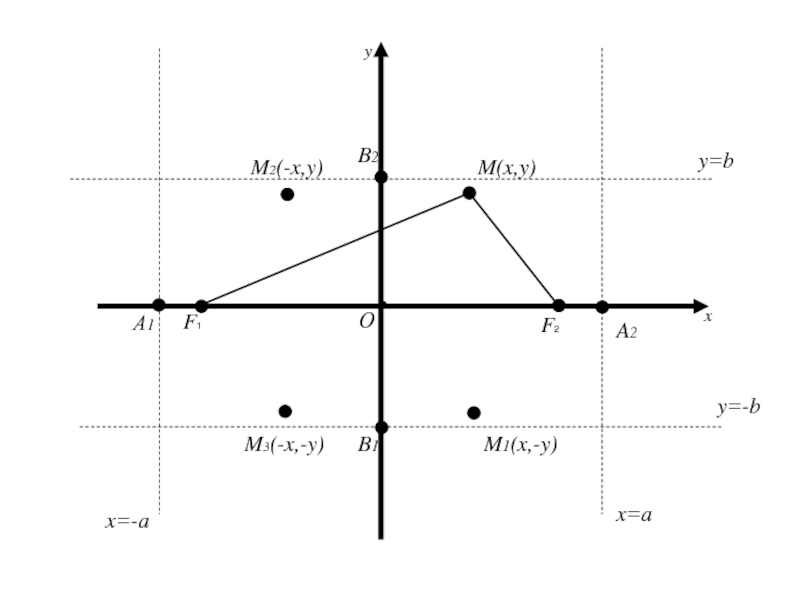
- 76. Точки пересечения эллипса с осями координат называются вершинами эллипса
- 77. Точки пересечения эллипса с осями координат называются
- 78. Точки пересечения эллипса с осями координат называются
- 79. Точки пересечения эллипса с осями координат называются
- 80. Отношение половины расстояния между фокусами эллипса (фокальное
- 81. Отношение половины расстояния между фокусами эллипса (фокальное
- 82. Отношение половины расстояния между фокусами эллипса (фокальное
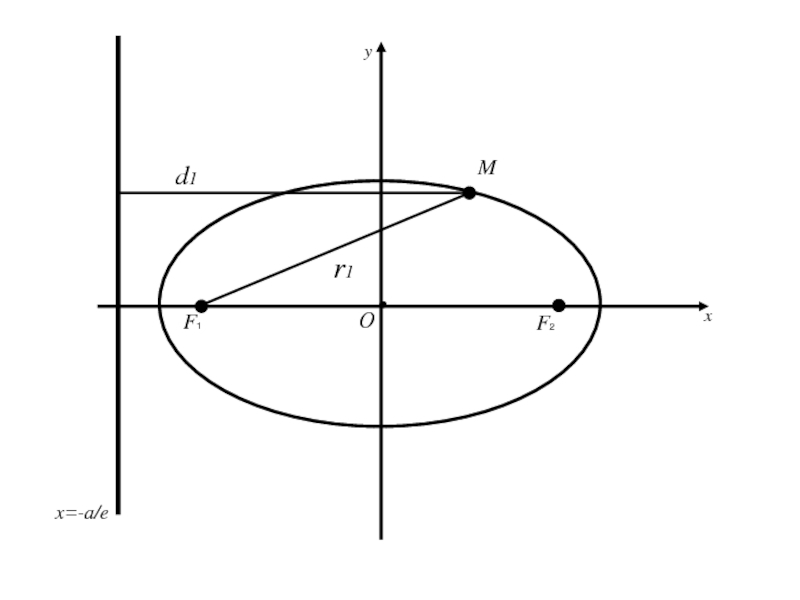
- 83. 3.Директрисы эллипса.Две прямые перпендикулярные оси эллипса, на
- 84. 3.Директрисы эллипса.Две прямые перпендикулярные оси эллипса, на
- 85. F1 F2 MОxy
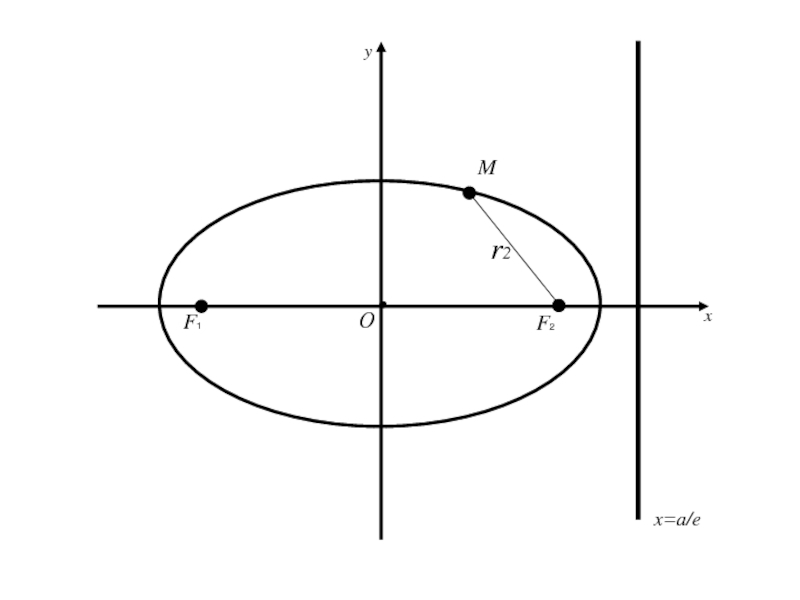
- 86. F1 F2 MОxyx=a/e
- 87. F1 F2 MОxyx=a/ex=-a/e
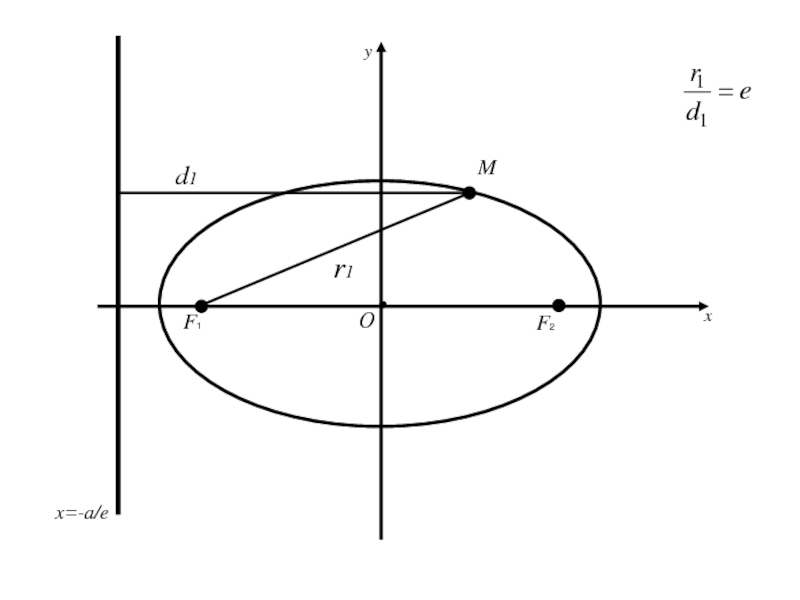
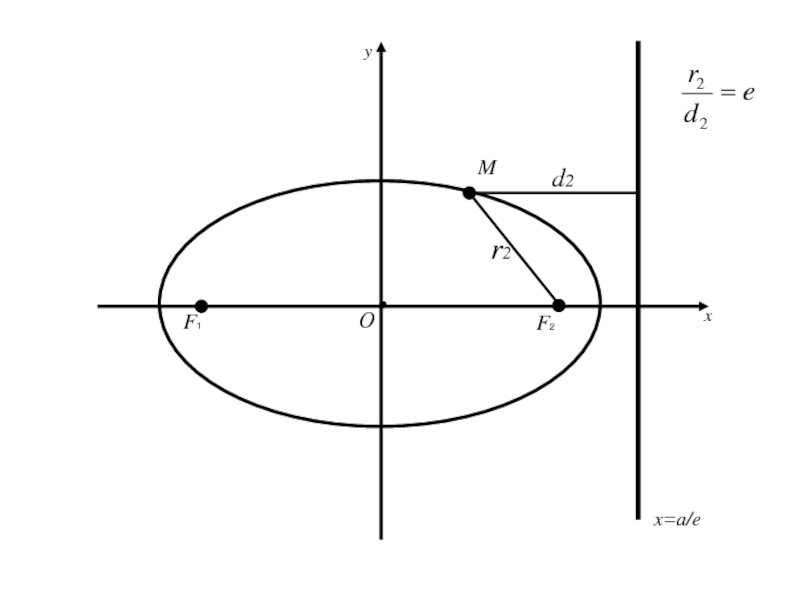
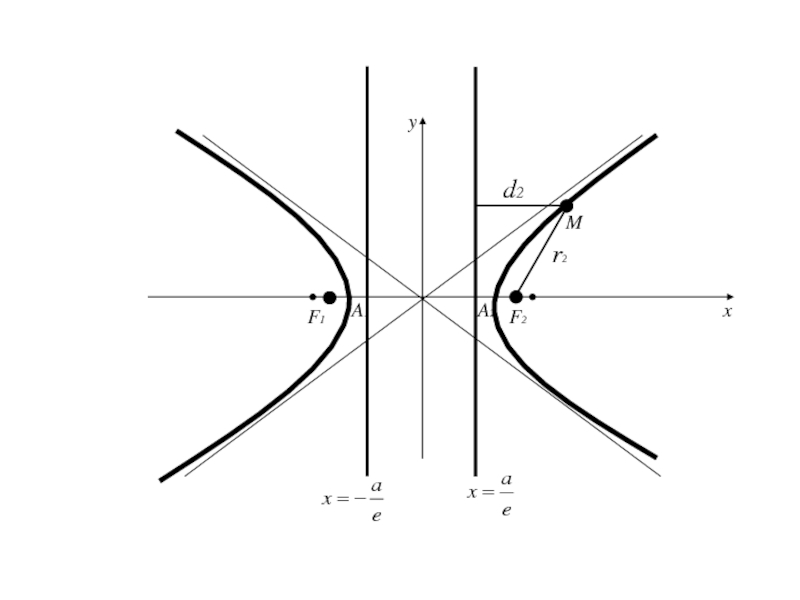
- 88. Теорема: Для того, чтобы точка лежала на
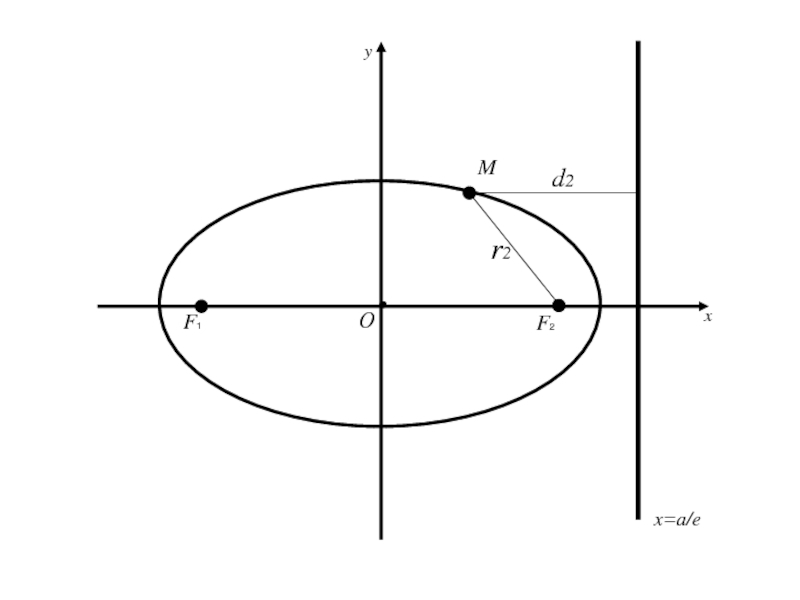
- 89. F1 F2 MОxyx=a/e
- 90. F1 F2 MОxyx=a/er2
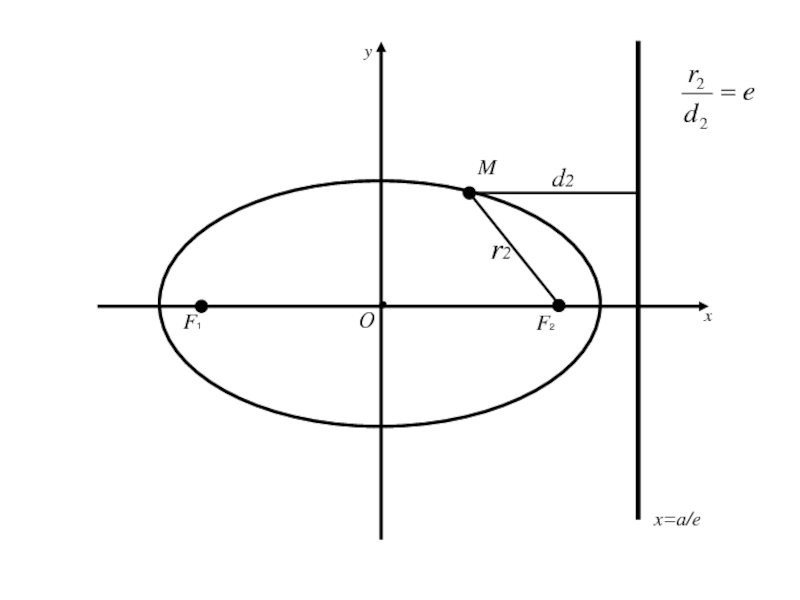
- 91. F1 F2 MОxyx=a/ed2r2
- 92. F1 F2 MОxyx=a/ed2r2
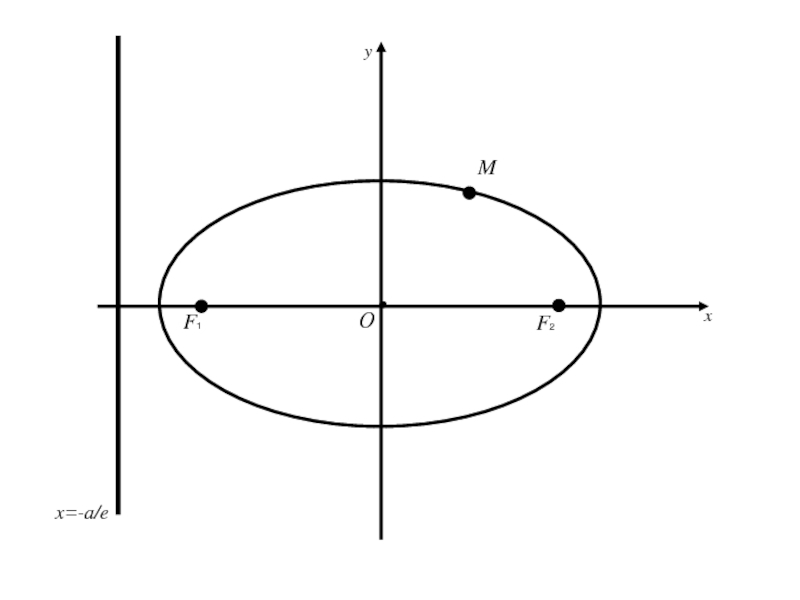
- 93. F1 F2 MОxyx=-a/e
- 94. F1 F2 MОxyx=-a/er1
- 95. F1 F2 MОxyx=-a/ed1r1
- 96. F1 F2 MОxyx=-a/ed1r1
- 97. F1 F2 MОxyx=a/ed2r2
- 98. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется
- 99. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняется
- 100. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что
- 101. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 102. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 103. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 104. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 105. (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой выполняетсятребуется доказать, что найдём
- 106. Пусть существует точка
- 107. Пусть существует точка
- 108. Пусть существует точка
- 109. Пусть существует точка
- 110. Пусть существует точка
- 111. Пусть существует точка
- 112. Самостоятельно изучить вопросы по данной теме:Вид эллипса в случае a
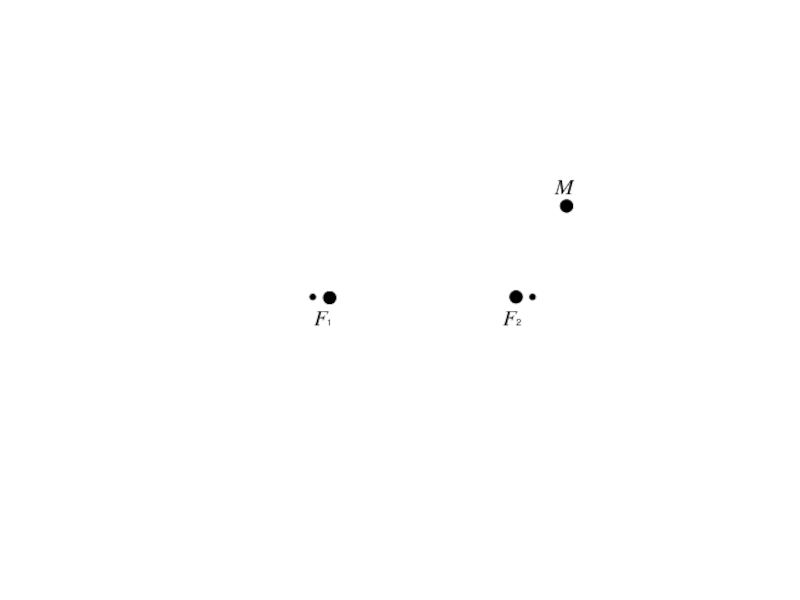
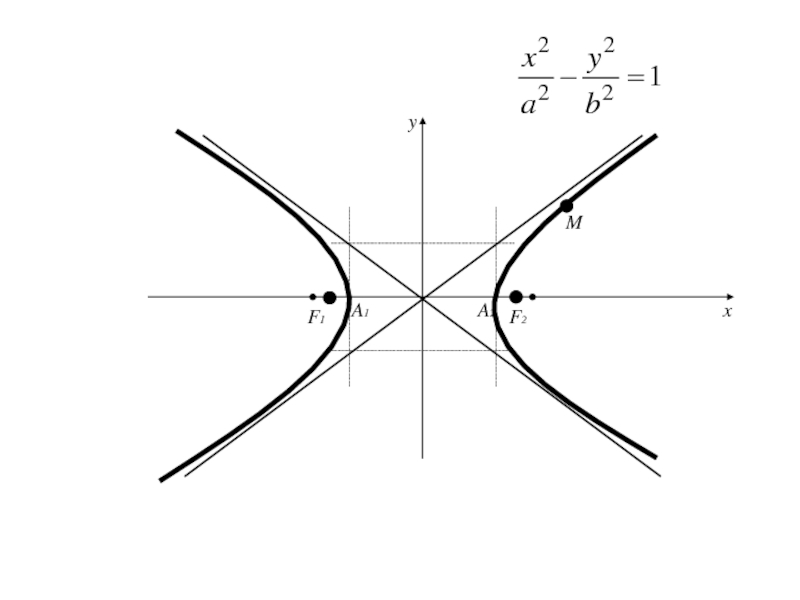
- 113. 4. Гипербола и её каноническое уравнениеГиперболой называется
- 114. M
- 115. F1 M
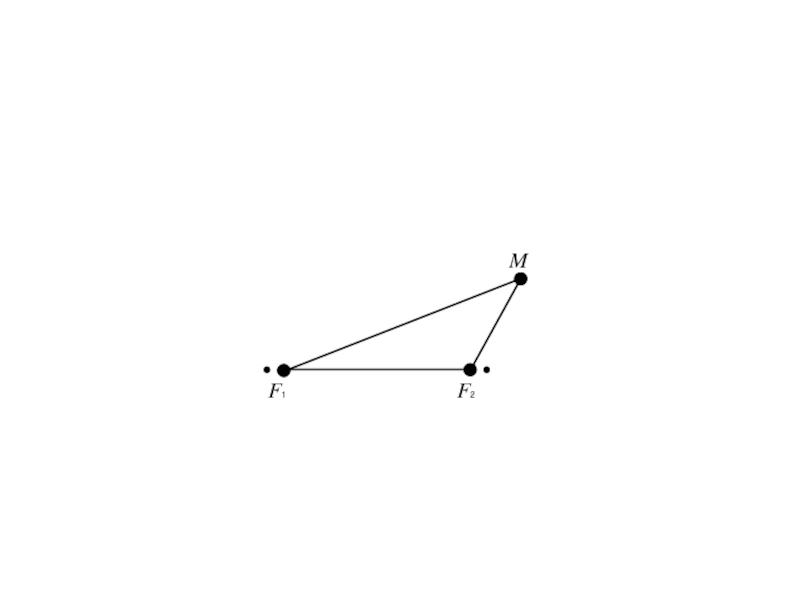
- 116. F1 F2 M
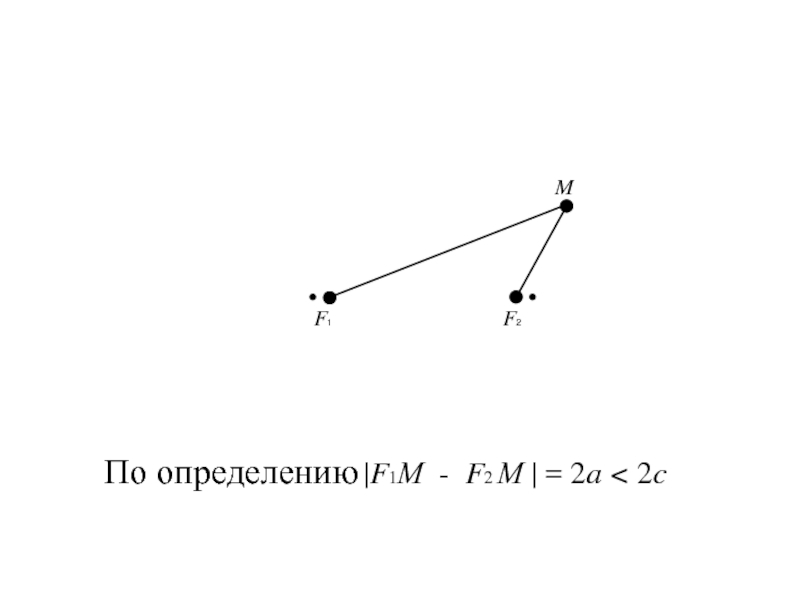
- 117. По определению |F1М - F2 М | = 2a < 2c
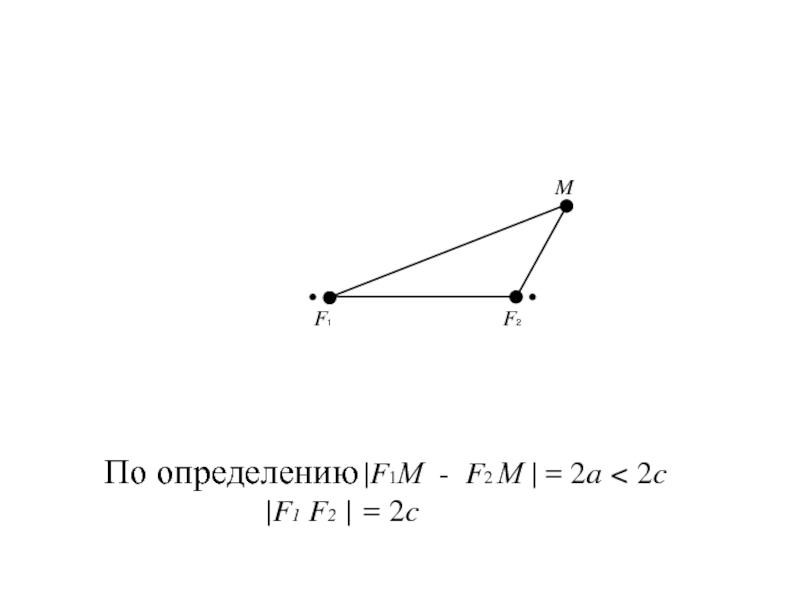
- 118. По определению |F1М - F2 М | = 2a < 2c |F1 F2 | = 2c
- 119. Слайд 119
- 120. Слайд 120
- 121. Слайд 121
- 122. x
- 123. x
- 124. xF1 F2 MО
- 125. xF1 F2 MОy
- 126. Так как |F1 F2 | = 2c,
- 127. Так как |F1 F2 | = 2c,
- 128. Так как |F1 F2 | = 2c,
- 129. Так как |F1 F2 | = 2c,
- 130. Так как |F1 F2 | = 2c,
- 131. По определению |F1М - F2 М | = 2a (1)Получим
- 132. По определению |F1М - F2М | = 2a (1) Получим
- 133. По определению |F1М - F2М | =
- 134. По определению |F1М - F2М | =
- 135. По определению |F1М - F2М | =
- 136. По определению |F1М - F2М | =
- 137. По определению |F1М - F2М | =
- 138. Слайд 138
- 139. Разделим на 4 и возведём обе части в квадрат
- 140. Разделим на 4 и возведём обе части в квадрат
- 141. Разделим на 4 и возведём обе части в квадрат
- 142. Разделим на 4 и возведём обе части в квадрат
- 143. Слайд 143
- 144. Так как по определению a < c, обозначим
- 145. Так как по определению a < c, обозначим
- 146. Так как по определению a < c, обозначимполучим выражение
- 147. Так как по определению a < c,
- 148. Так как по определению a < c,
- 149. Мы доказали, что координаты любой точки гиперболы удовлетворяют уравнению (2)
- 150. Докажем обратное: если координаты некоторой точки М(x,y)
- 151. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
- 152. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
- 153. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
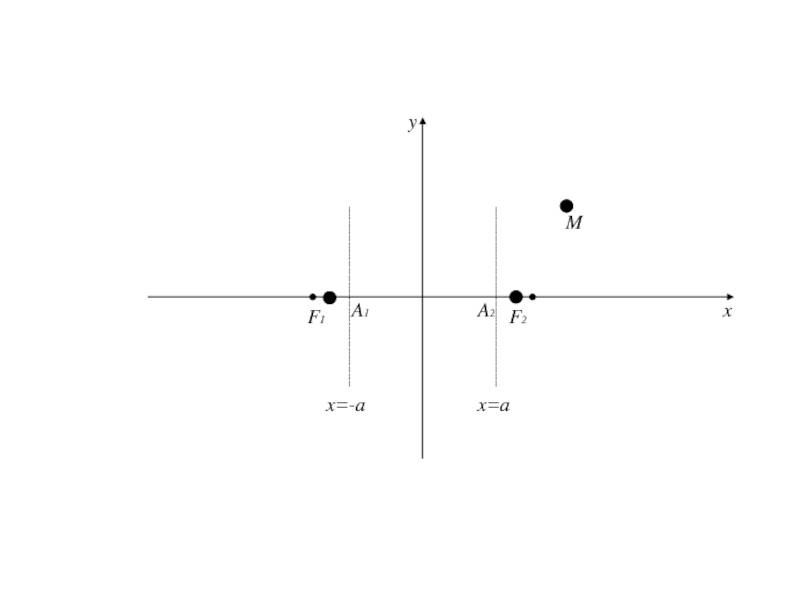
- 154. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
- 155. Так как ,
- 156. Так как , значит
- 157. Так как
- 158. Так как
- 159. Так как
- 160. Так как
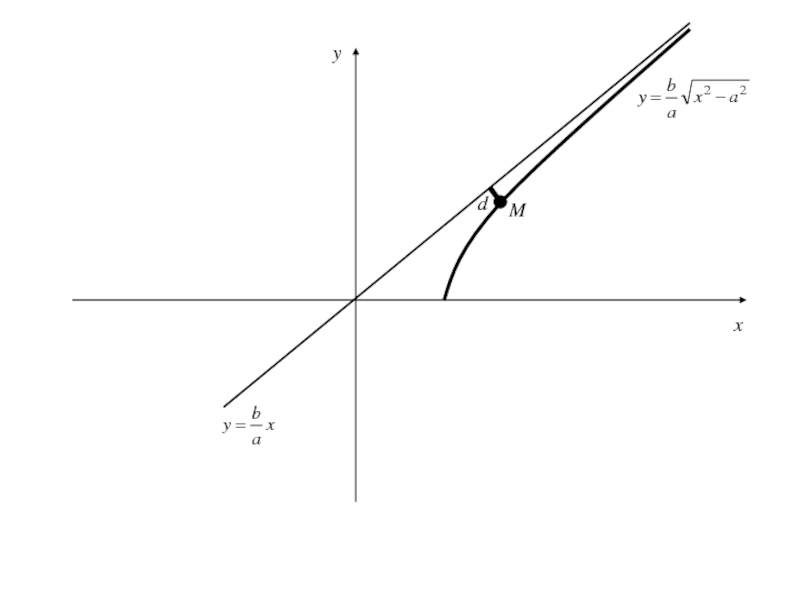
- 161. Отрезки F1M и F2M назовем фокальными радиусами гиперболы
- 162. Отрезки F1M и F2M назовем фокальными радиусами гиперболы
- 163. Отрезки F1M и F2M назовем фокальными радиусами
- 164. Отрезки F1M и F2M назовем фокальными радиусами
- 165. Отрезки F1M и F2M назовем фокальными радиусами
- 166. Отрезки F1M и F2M назовем фокальными радиусами
- 167. Отрезки F1M и F2M назовем фокальными радиусами
- 168. Отрезки F1M и F2M назовем фокальными радиусами
- 169. Отрезки F1M и F2M назовем фокальными радиусами
- 170. Таким образом, получаем если
- 171. Таким образом, получаем если
- 172. Таким образом, получаем если
- 173. Таким образом, получаем если
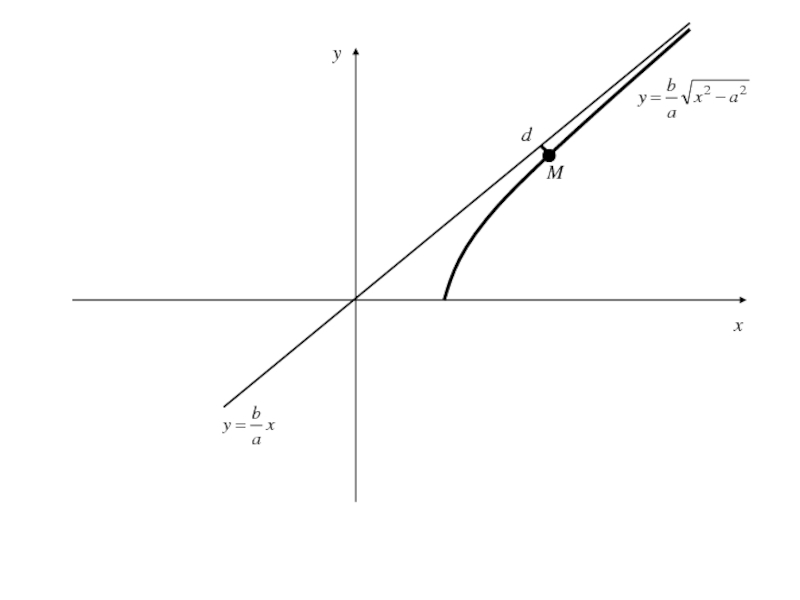
- 174. Таким образом, получаем если
- 175. Таким образом, получаем если
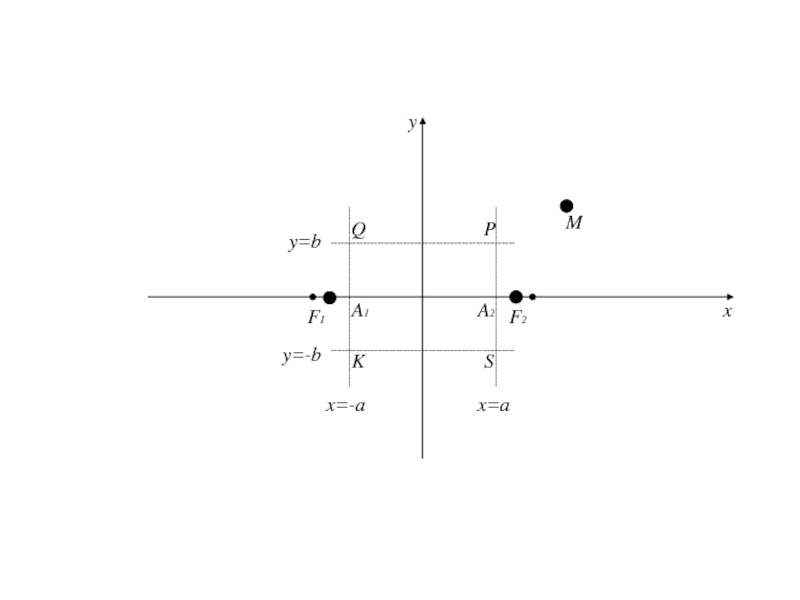
- 176. Таким образом, получаем если
- 177. Таким образом, получаем если
- 178. Таким образом, уравнение (2) есть уравнение гиперболы,
- 179. каноническое уравнение гиперболы
- 180. каноническое уравнение гиперболы
- 181. 5. Исследование формы гиперболы
- 182. 5. Исследование формы гиперболыТ.к. в каноническое уравнение гиперболы координаты x и y входят во второй степени
- 183. 5. Исследование формы гиперболыТ.к. в каноническое уравнение
- 184. Из уравнения => что
- 185. Из уравнения => что
- 186. Ось симметрии Ox пересекает гиперболу в двух
- 187. Ось симметрии Ox пересекает гиперболу в двух
- 188. Выразим y из уравнения гиперболы и возьмем положительное значение
- 189. Выразим y из уравнения гиперболы и возьмем
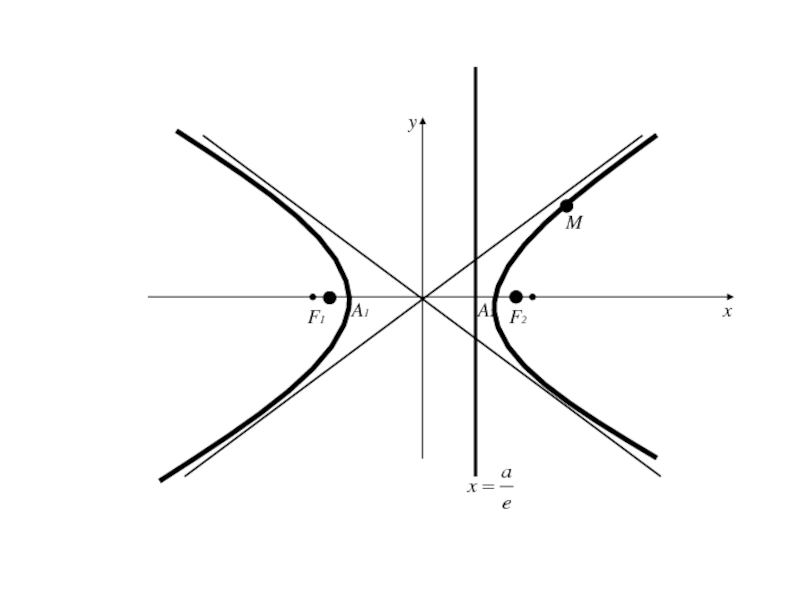
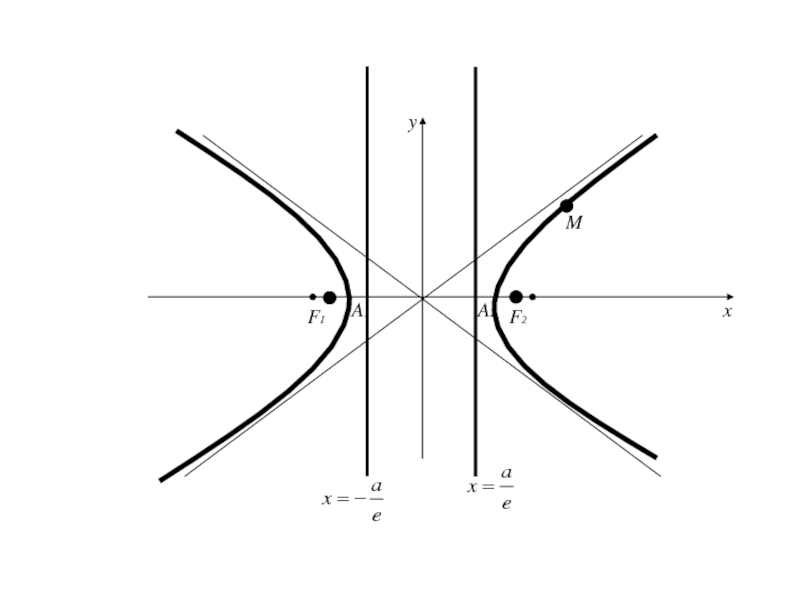
- 190. Выразим y из уравнения гиперболы и возьмем
- 191. Выразим y из уравнения гиперболы и возьмем
- 192. Выразим y из уравнения гиперболы и возьмем
- 193. Всякая прямая пересекает гиперболу не более чем
- 194. Рассмотрим уравнение прямой
- 195. Рассмотрим уравнение прямой
- 196. Рассмотрим уравнение прямой
- 197. Рассмотрим уравнение прямой
- 198. Рассмотрим уравнение прямой
- 199. Получили, что на полуинтервале
- 200. Получили, что на полуинтервале
- 201. xy
- 202. xy
- 203. xyM
- 204. xyMd
- 205. xyMd
- 206. В силу того, что гипербола, заданная каноническим
- 207. Так как гипербола, заданная каноническим уравнением, симметрична
- 208. x=-aA1A2F1F2Mxyx=a
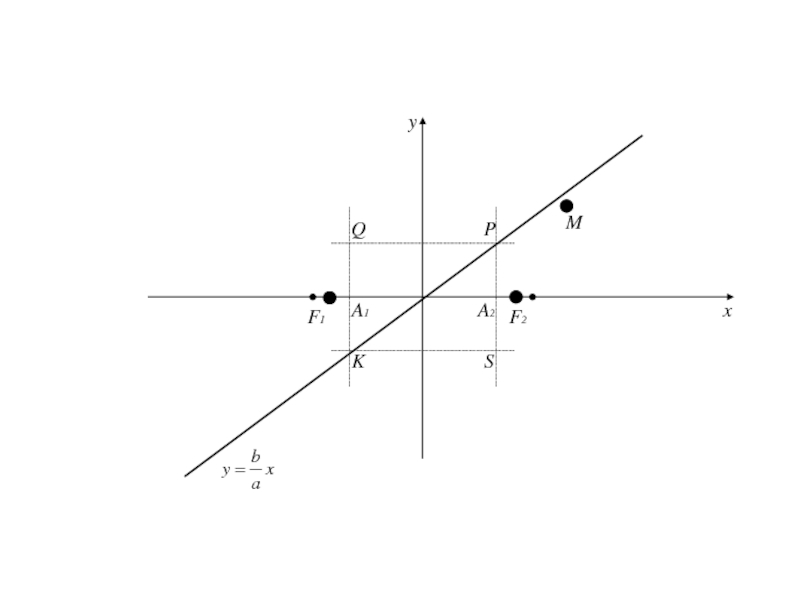
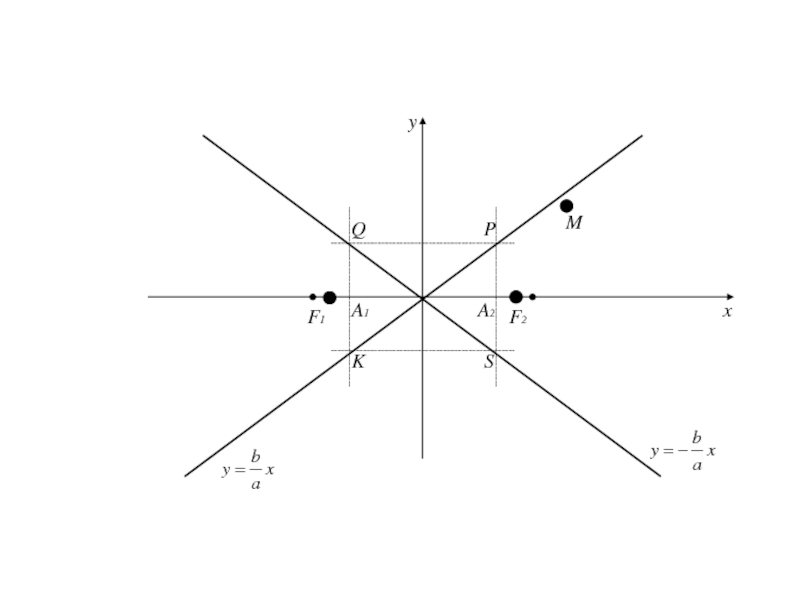
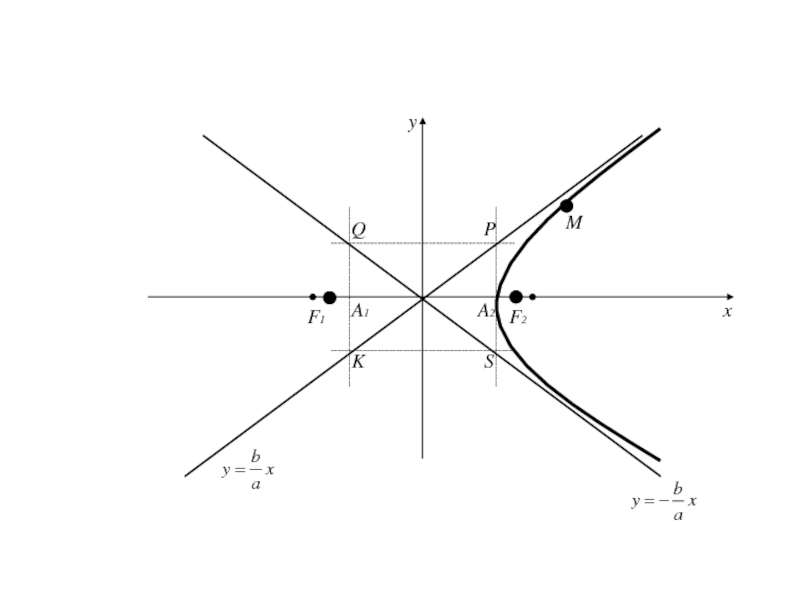
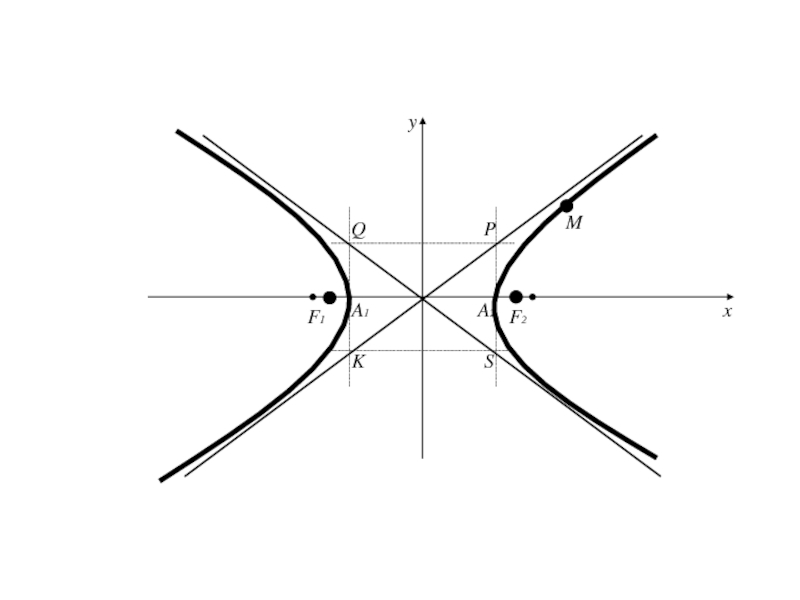
- 209. PQSKA1A2F1F2Mxyx=-ax=ay=-by=b
- 210. PQSKA1A2F1F2Mxy
- 211. PQSKA1A2F1F2Mxy
- 212. PQSKA1A2F1F2Mxy
- 213. PQSKA1A2F1F2Mxy
- 214. A1A2F1F2Mxy
- 215. Гипербола, у которой полуоси равны, называется равностороннейУравнения её асимптот
- 216. 6. Эксцентриситет и директрисы гиперболы
- 217. 6. Эксцентриситет и директрисы гиперболы Отношение расстояния
- 218. 6. Эксцентриситет и директрисы гиперболы Отношение расстояния
- 219. 6. Эксцентриситет и директрисы гиперболы Отношение расстояния
- 220. Перепишем формулы для фокальных радиусов если
- 221. Перепишем формулы для фокальных радиусов если
- 222. Две прямые, перпендикулярные действительной оси гиперболы и
- 223. Для гиперболы, заданной каноническим уравнениемуравнения директрис имеют вид
- 224. Для гиперболы, заданной каноническим уравнениемуравнения директрис имеют
- 225. A1A2F1F2Mxy
- 226. A1A2F1F2Mxy
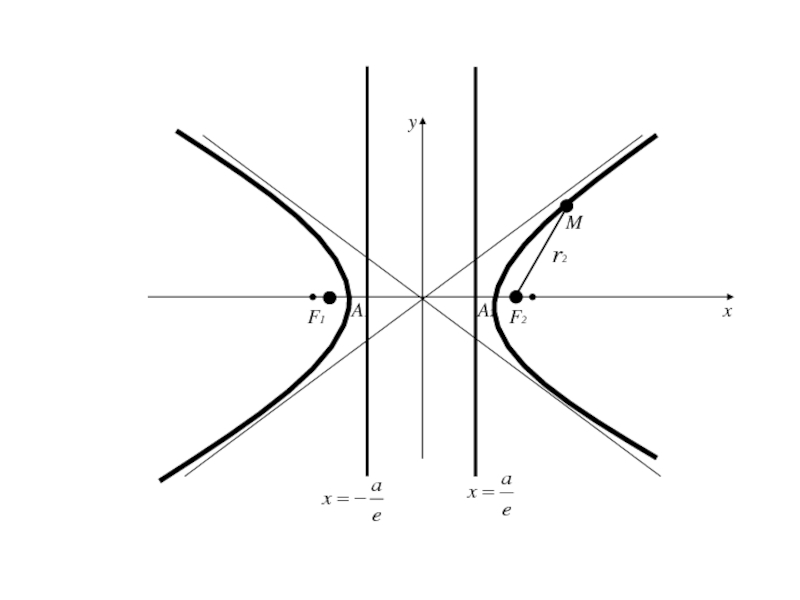
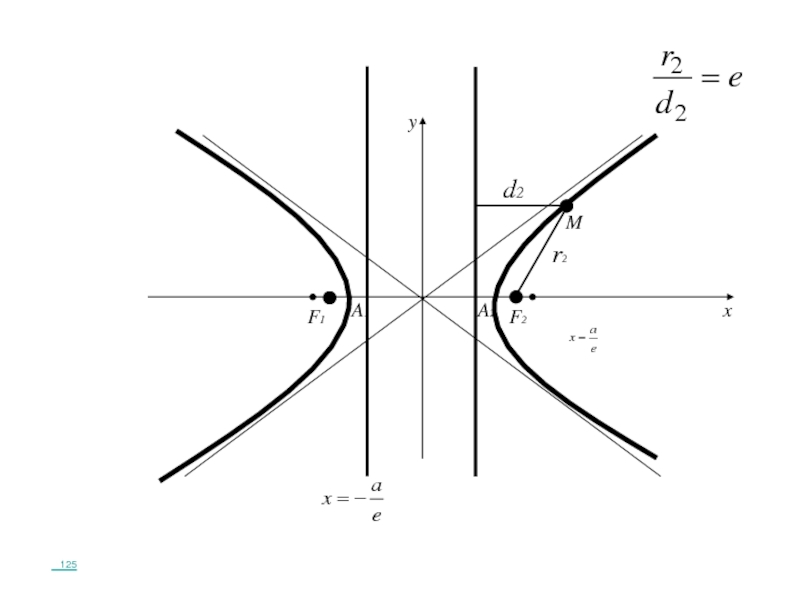
- 227. Теорема: Для того чтобы точка лежала на
- 228. A1A2F1F2Mxyr2
- 229. A1A2F1F2Mxyr2d2
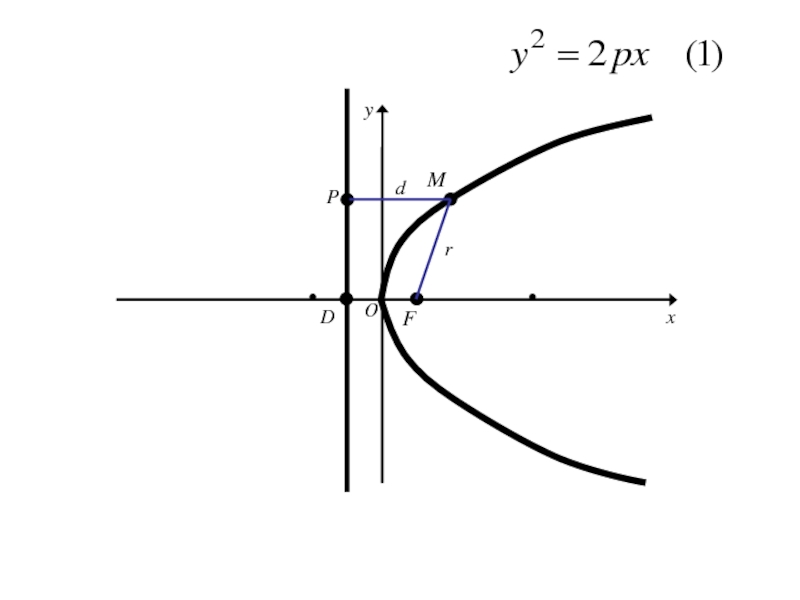
- 230. A1A2F1F2Mxyr2d2 125
- 231. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняется
- 232. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняется
- 233. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняетсятребуется доказать, что
- 234. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняетсятребуется доказать, что Найдём
- 235. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняетсятребуется доказать, что найдём
- 236. (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой выполняетсятребуется доказать, что найдём
- 237. Пусть существует точка
- 238. Пусть существует точка
- 239. Пусть существует точка
- 240. Пусть существует точка
- 241. Пусть существует точка
- 242. Пусть существует точка
- 243. Самостоятельно изучить вопросы по данной теме:Понятие сопряженной гиперболыУравнение касательной к гиперболеОптическое свойство гиперболы
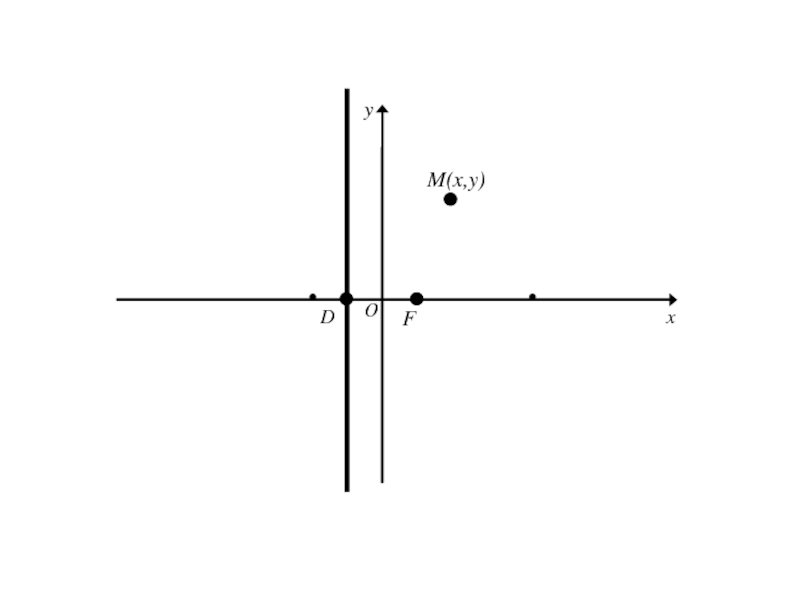
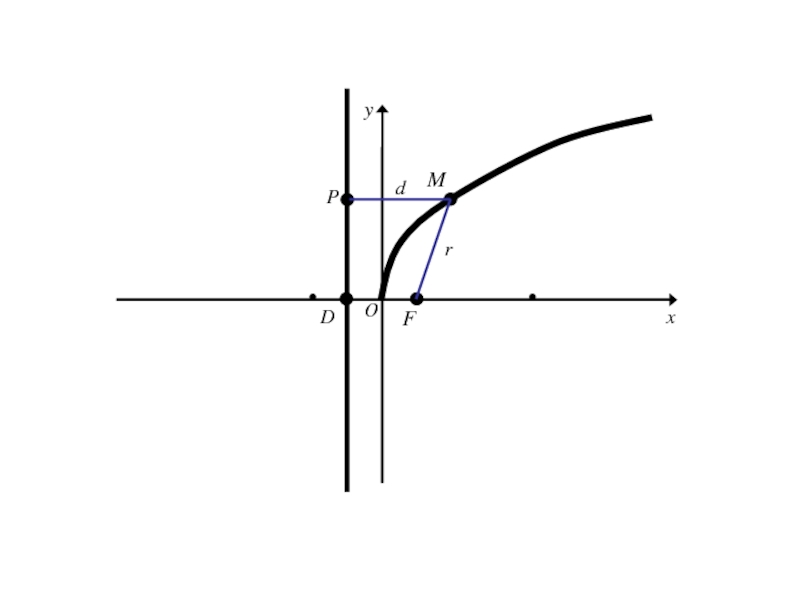
- 244. 7. Парабола и её каноническое уравнение Параболой
- 245. 7. Парабола и её каноническое уравнение Расстояние от фокуса параболы до её директрисы называется параметром параболы.
- 246. 7. Парабола и её каноническое уравнение Расстояние
- 247. F
- 248. F
- 249. F
- 250. FD
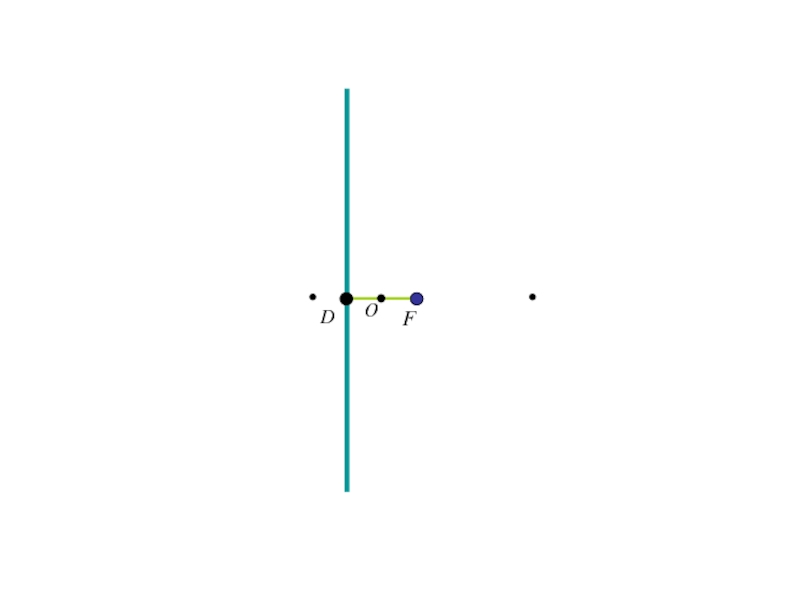
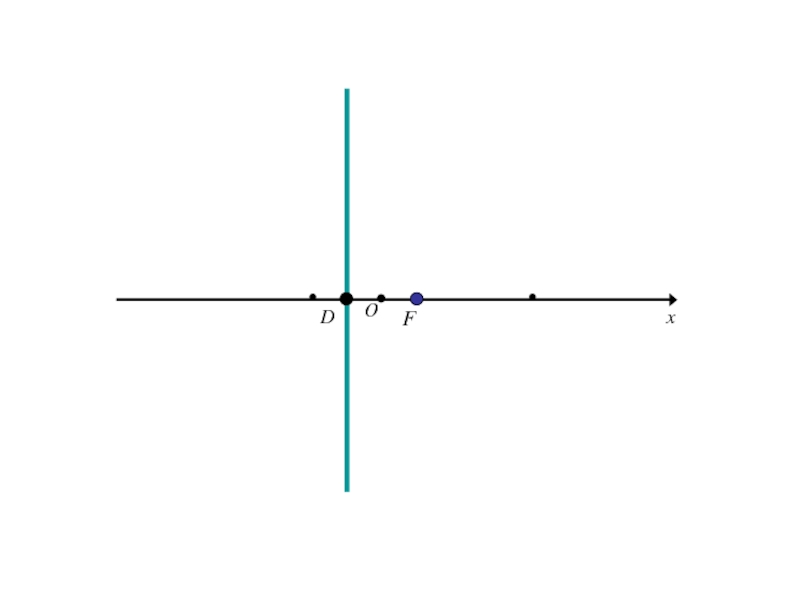
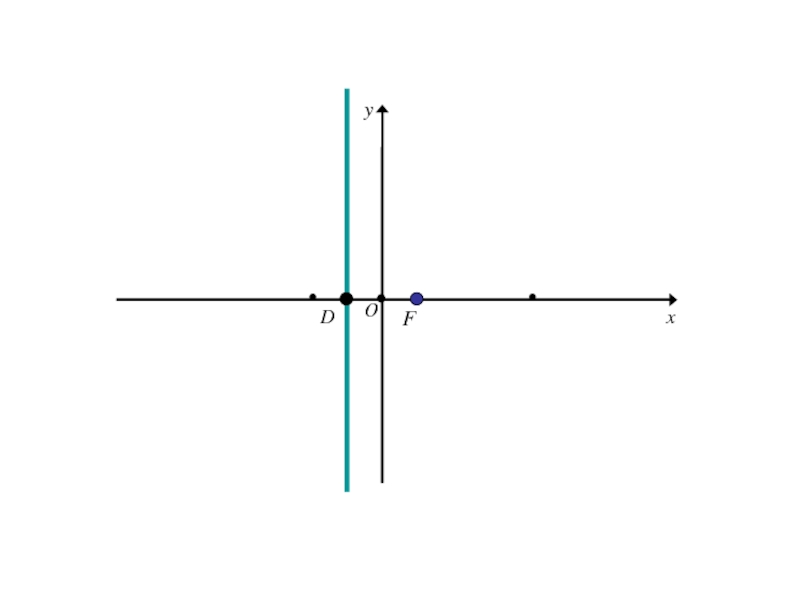
- 251. FDO
- 252. FDOx
- 253. FDOxy
- 254. Расстояние FD обозначим р (параметр параболы).
- 255. Расстояние FD обозначим р (параметр параболы).тогда в выбранной системе координат фокус F будет иметь координаты
- 256. Расстояние FD обозначим р (параметр параболы).тогда в
- 257. Расстояние FD обозначим р (параметр параболы).тогда в
- 258. Расстояние FD обозначим р (параметр параболы).тогда в
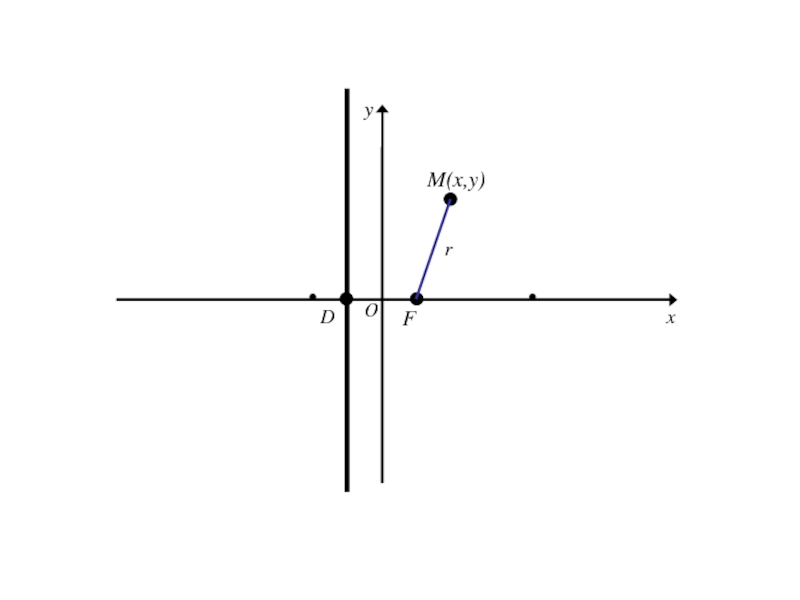
- 259. M(x,y)FDOxy
- 260. M(x,y)FDOxyr
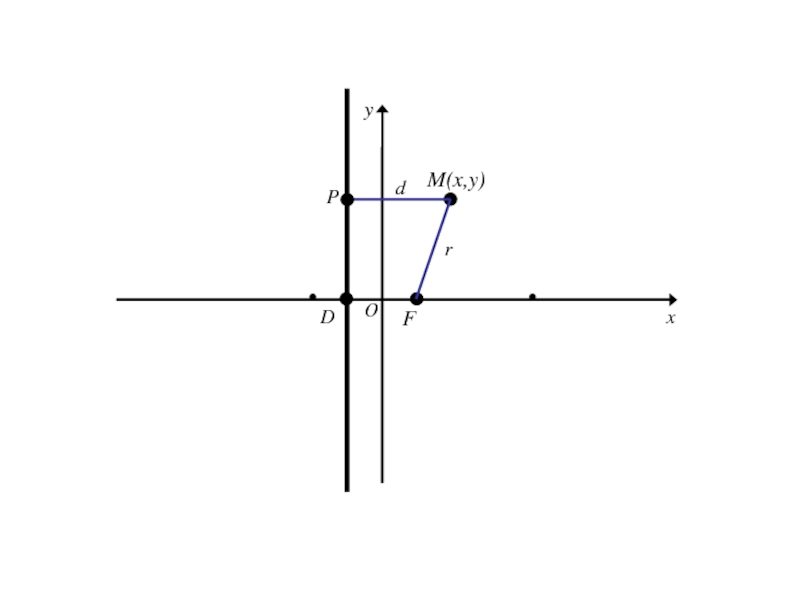
- 261. M(x,y)FDOxyrPd
- 262. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d
- 263. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d r=|FM|=
- 264. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d r=|FM|=
- 265. Точка M(x;y) лежит на данной параболе тогда
- 266. Точка M(x;y) лежит на данной параболе тогда
- 267. Точка M(x;y) лежит на данной параболе тогда
- 268. Слайд 268
- 269. Слайд 269
- 270. Слайд 270
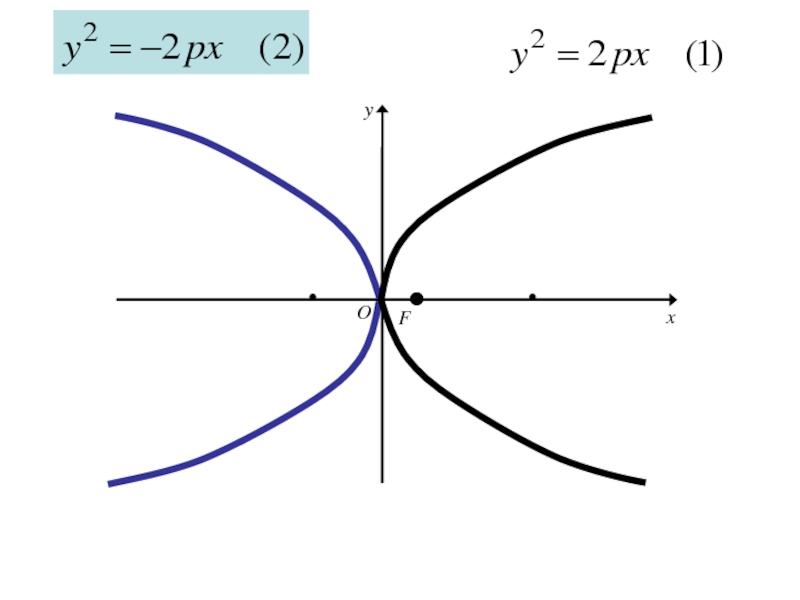
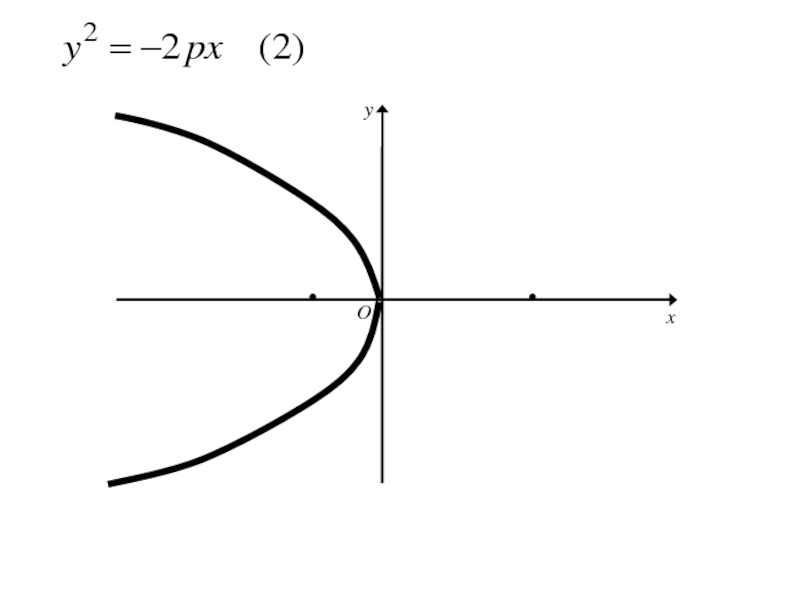
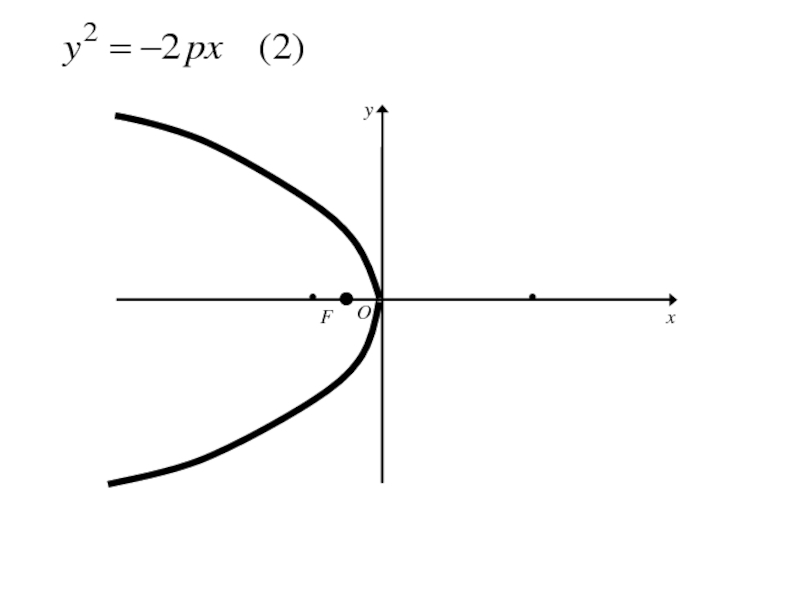
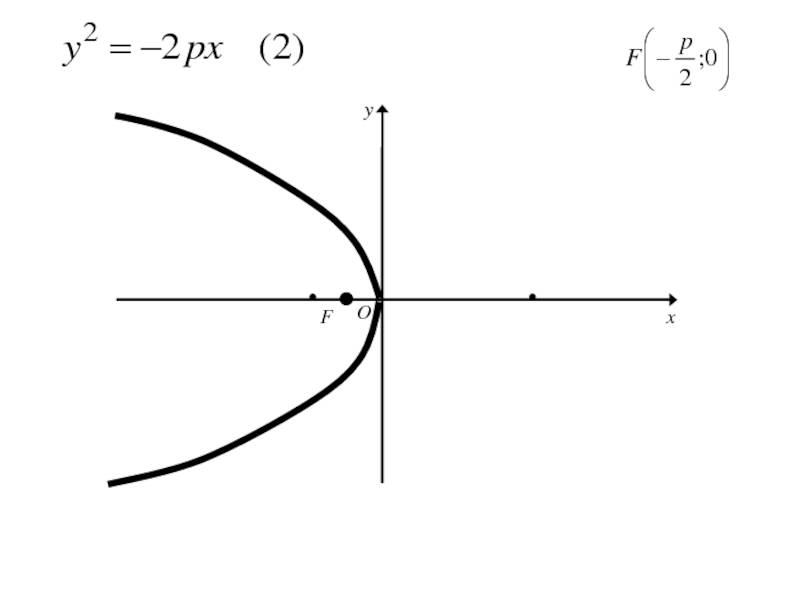
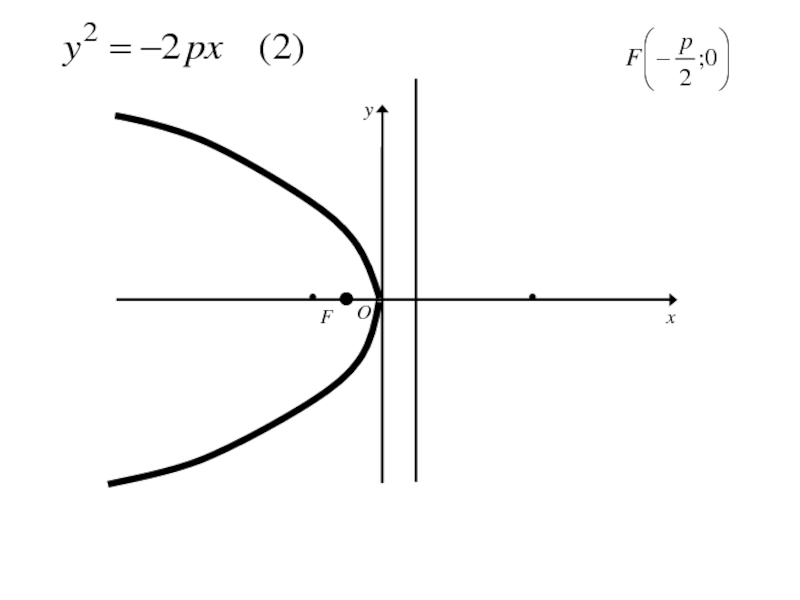
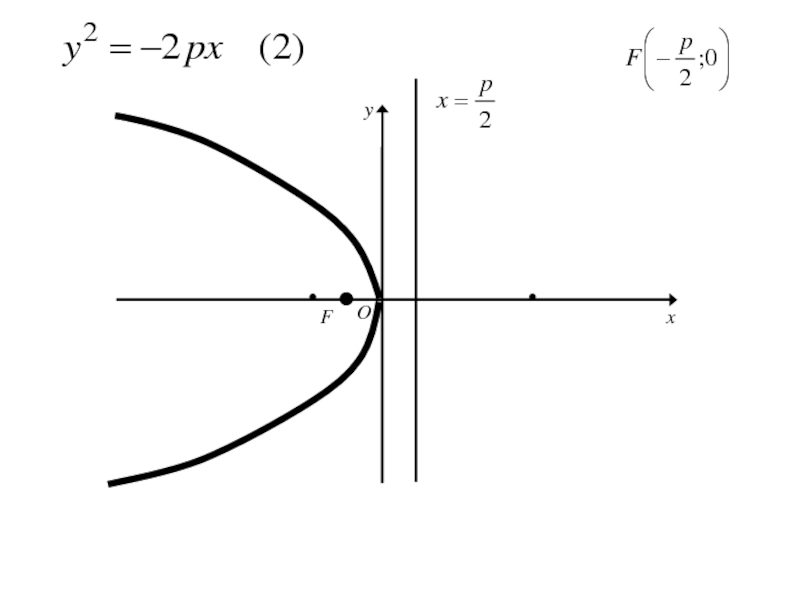
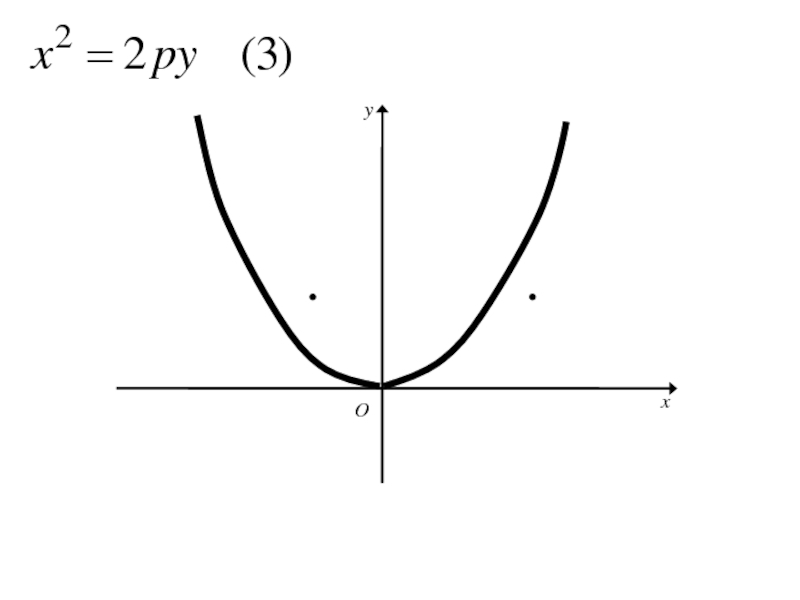
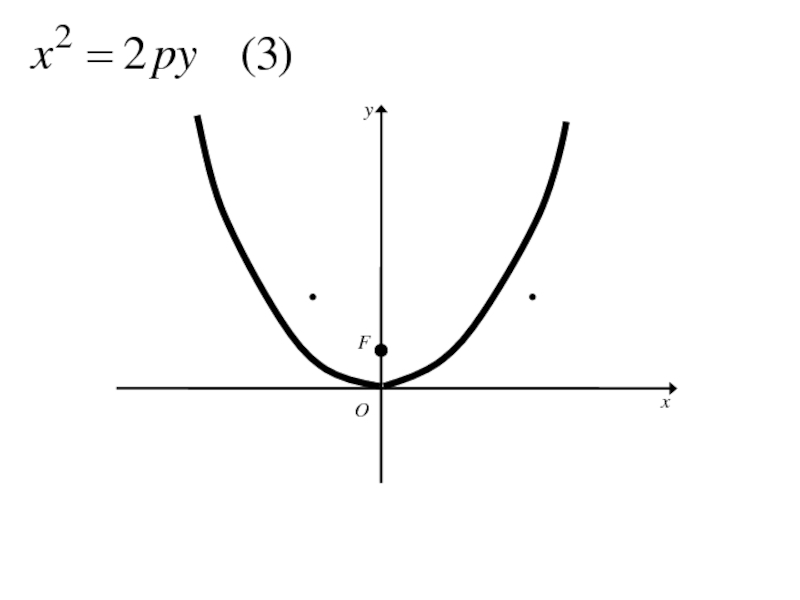
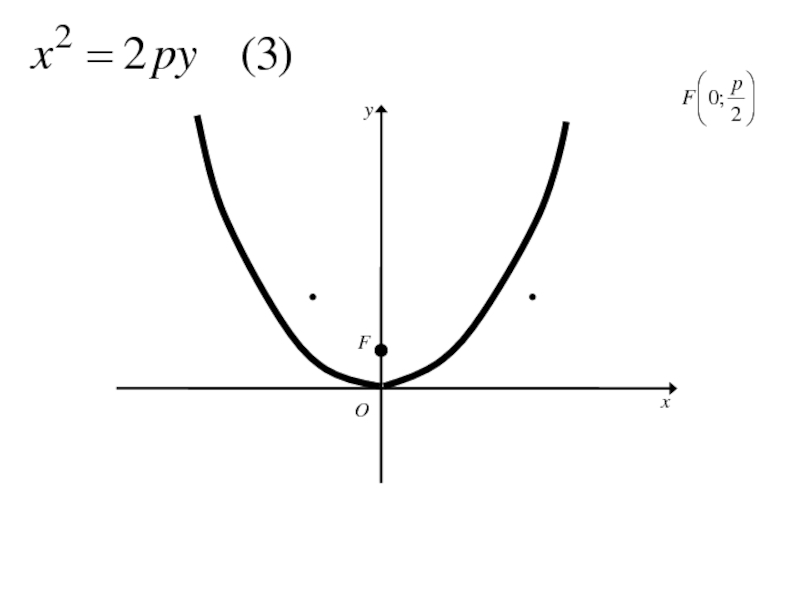
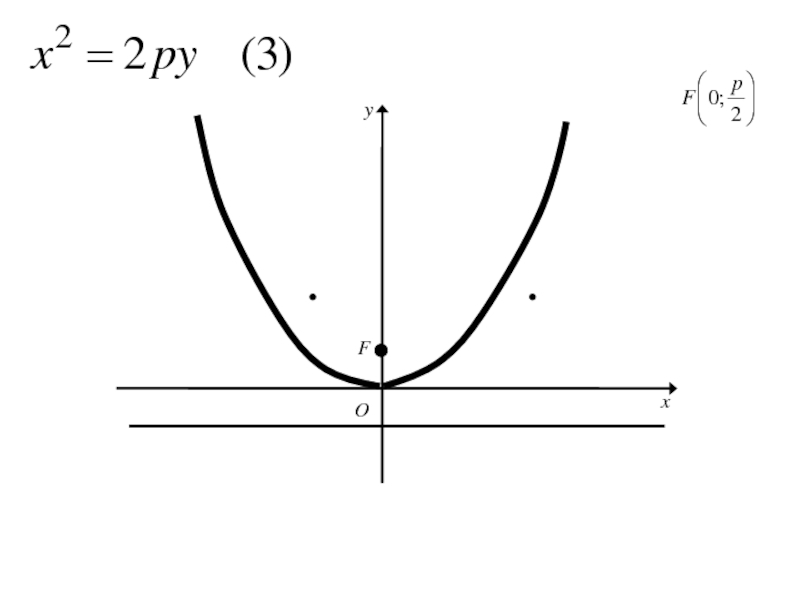
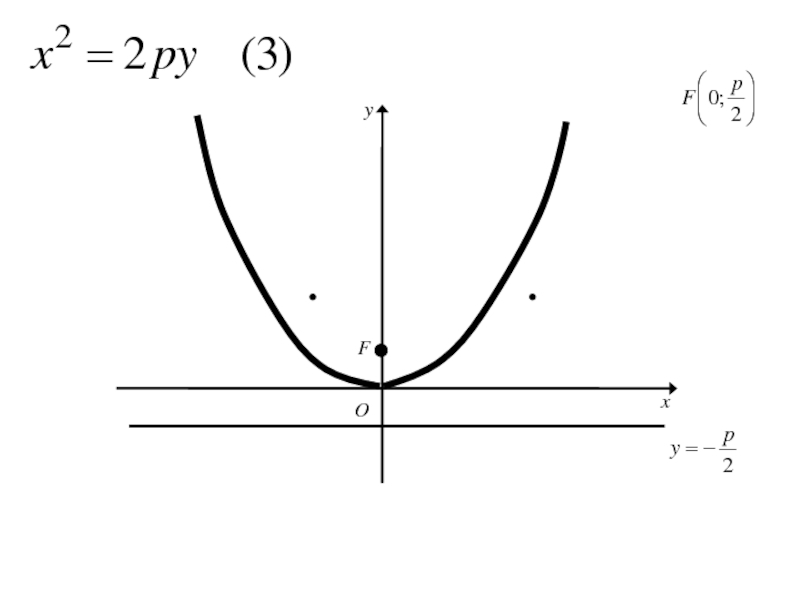
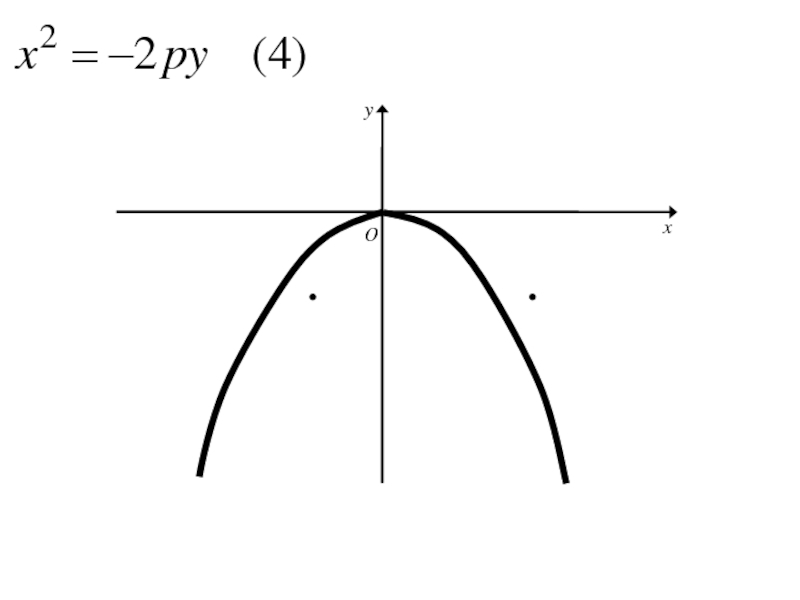
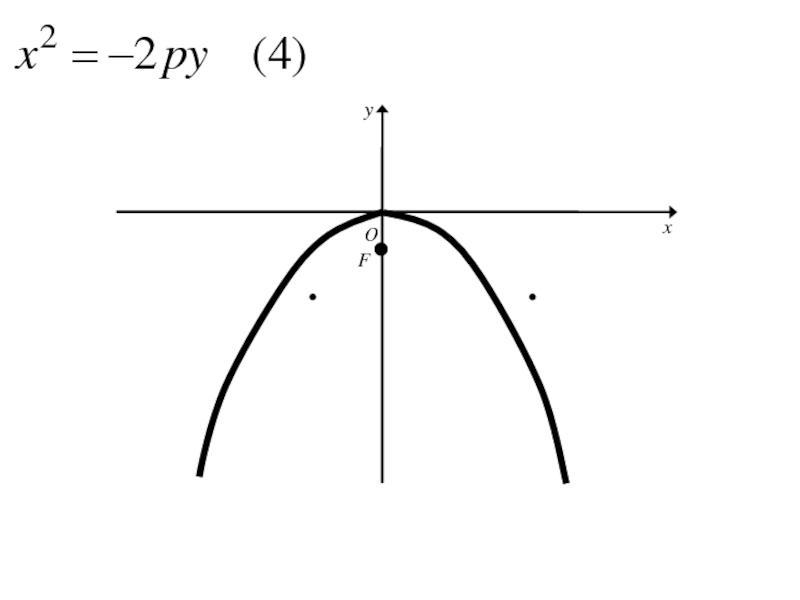
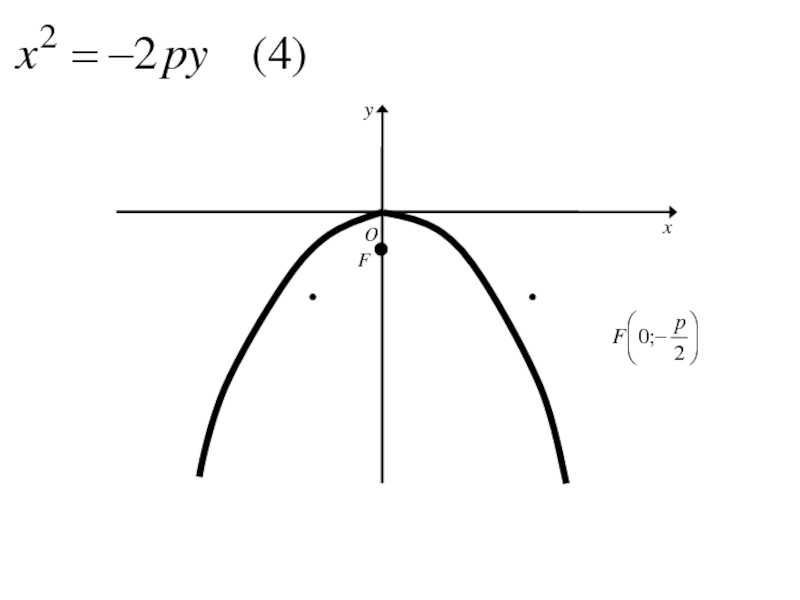
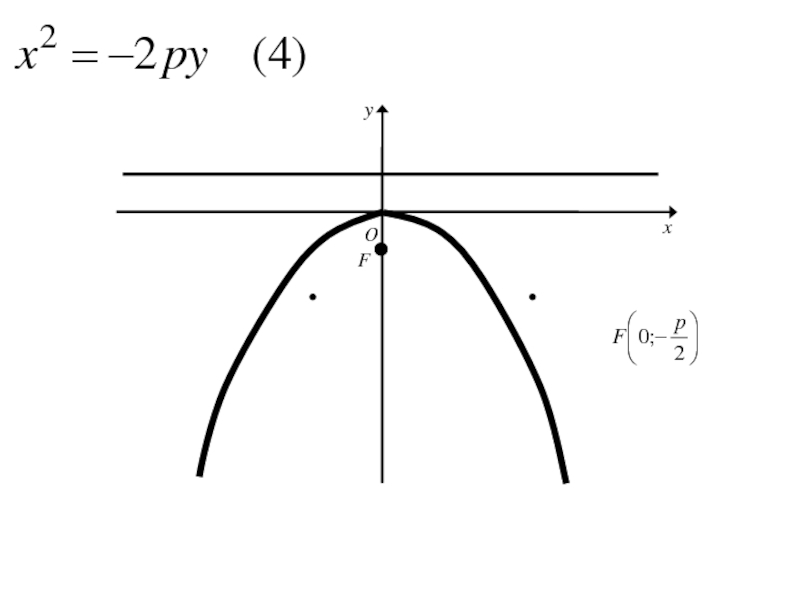
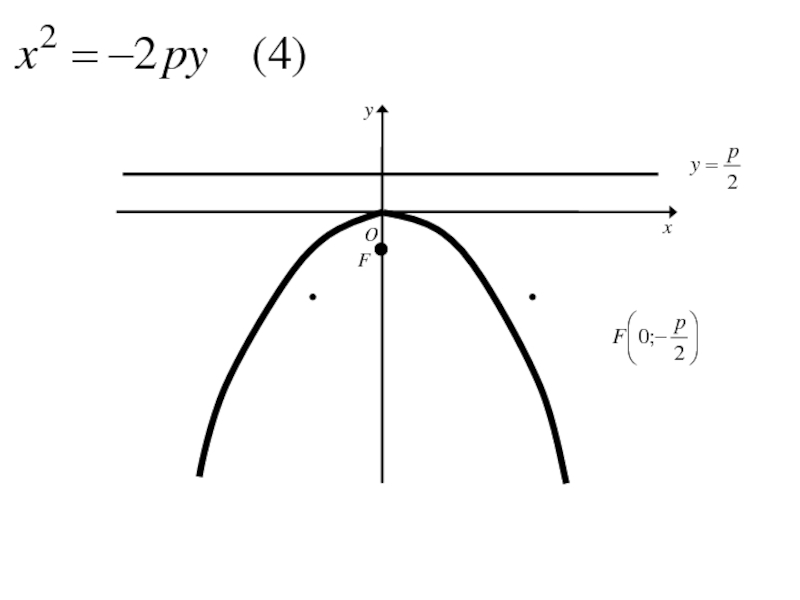
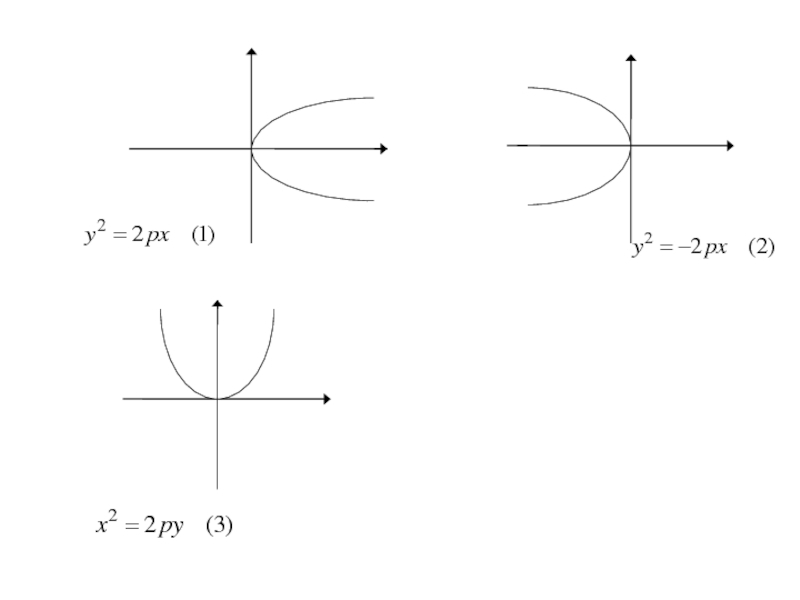
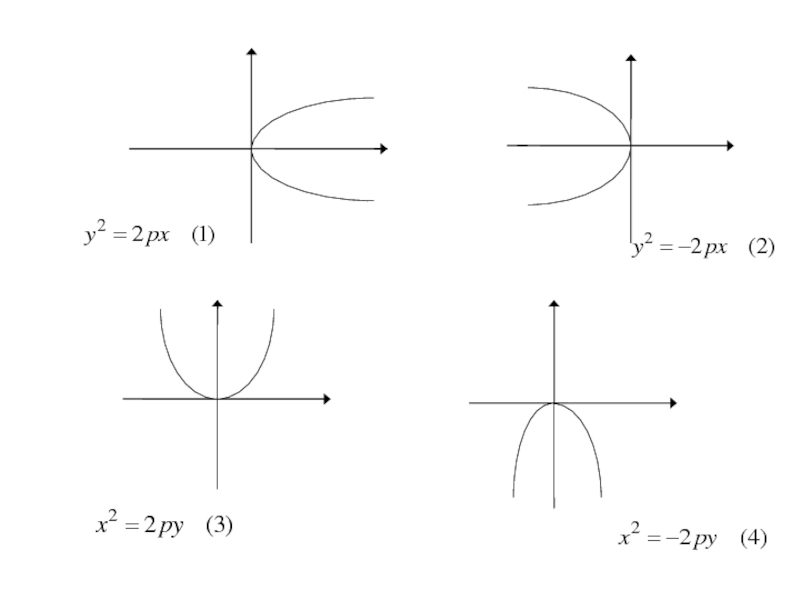
- 271. Каноническое уравнение параболы
- 272. Каноническое уравнение параболы
- 273. 8. Исследование формы параболы
- 274. 8. Исследование формы параболыТ.к. ордината у в каноническом уравнении параболы входит во 2-й степени, то
- 275. 8. Исследование формы параболыТ.к. ордината у в
- 276. 8. Исследование формы параболыТ.к. ордината у в
- 277. 8. Исследование формы параболыТ.к. ордината у в
- 278. 8. Исследование формы параболыТ.к. ордината у в
- 279. 8. Исследование формы параболыВсякая прямая пересекает параболу не более чем в двух точках
- 280. 8. Исследование формы параболыВсякая прямая пересекает параболу
- 281. Из (1) ⇒, что x≥0
- 282. Из (1) ⇒, что x≥0 (т. к. p>0, а
- 283. Из (1) ⇒, что x≥0 (т. к.
- 284. Из (1) ⇒, что x≥0 (т. к.
- 285. Из (1) ⇒, что x≥0 (т. к.
- 286. Из (1) ⇒, что x≥0 (т. к.
- 287. Из (1) ⇒, что x≥0 (т. к.
- 288. MFDOxyPrd
- 289. MFDOxyPrd
- 290. MFDOxyPrd
- 291. Уравнение
- 292. Уравнение
- 293. Уравнение
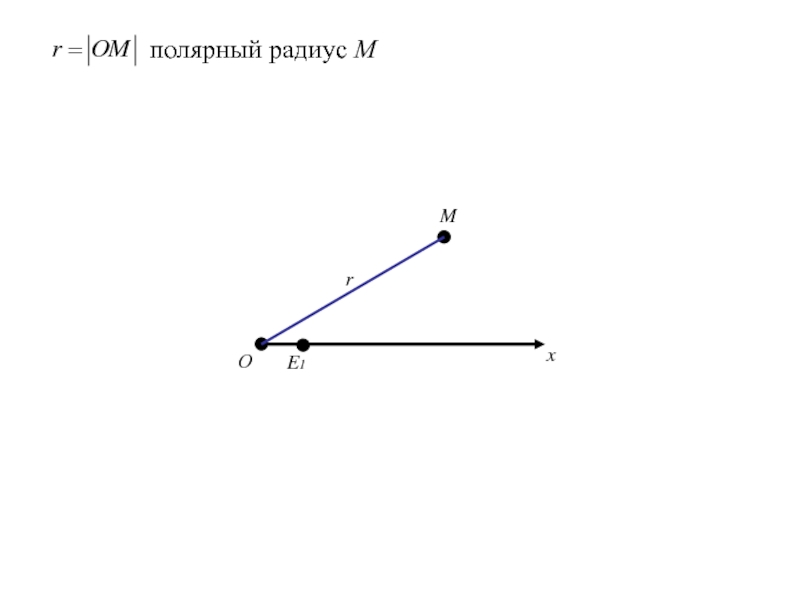
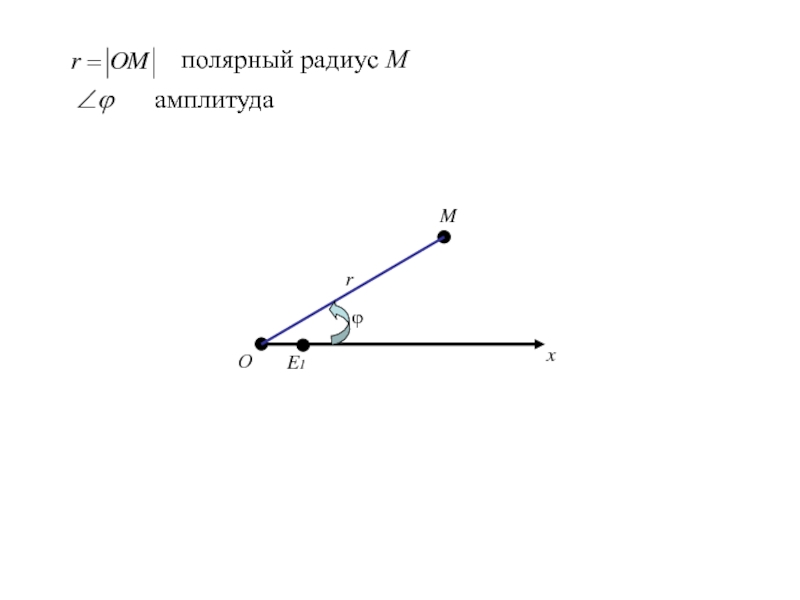
- 294. Уравнение
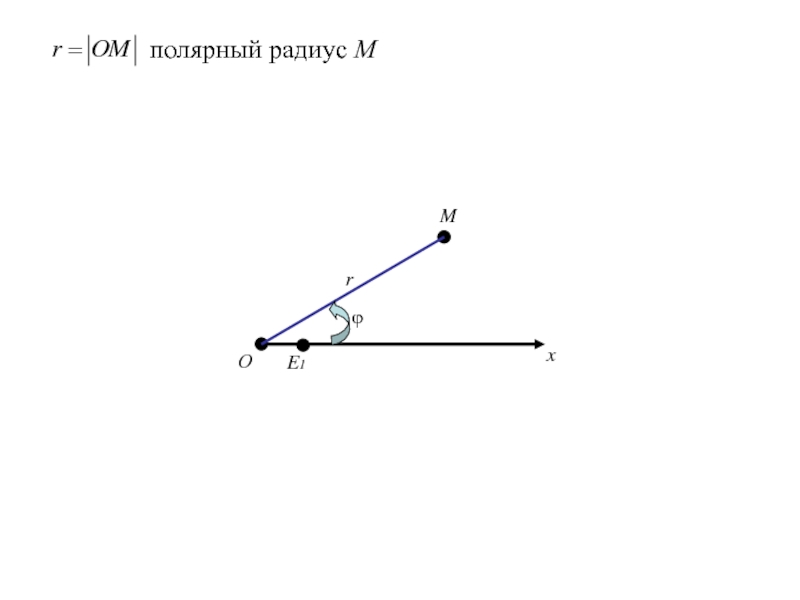
- 295. FOxy
- 296. FOxy
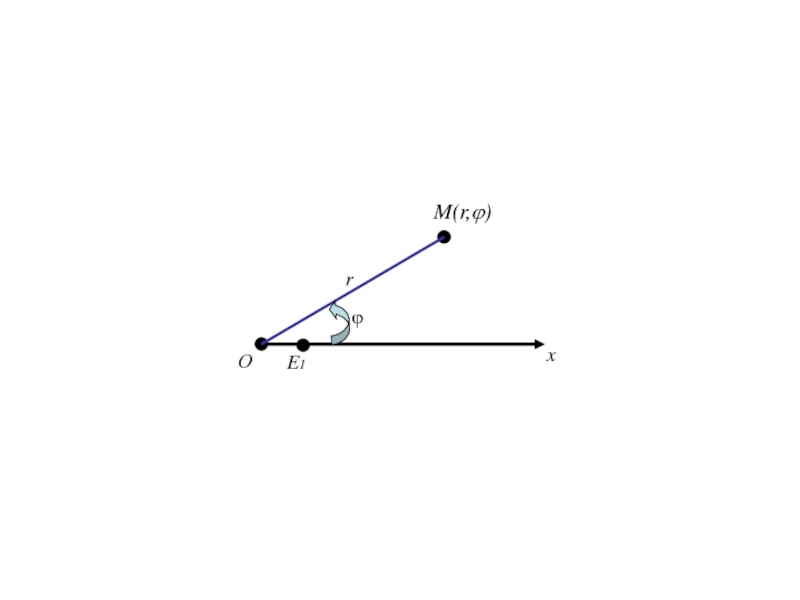
- 297. FOxy
- 298. Oxy
- 299. FOxy
- 300. FOxy
- 301. FOxy
- 302. FOxy
- 303. Аналогичными рассуждениями устанавливаем, что каждое из уравнений
- 304. Oxy
- 305. FOxy
- 306. FOxy
- 307. FOxy
- 308. FOxy
- 309. Oxy
- 310. OxyF
- 311. OxyF
- 312. OxyF
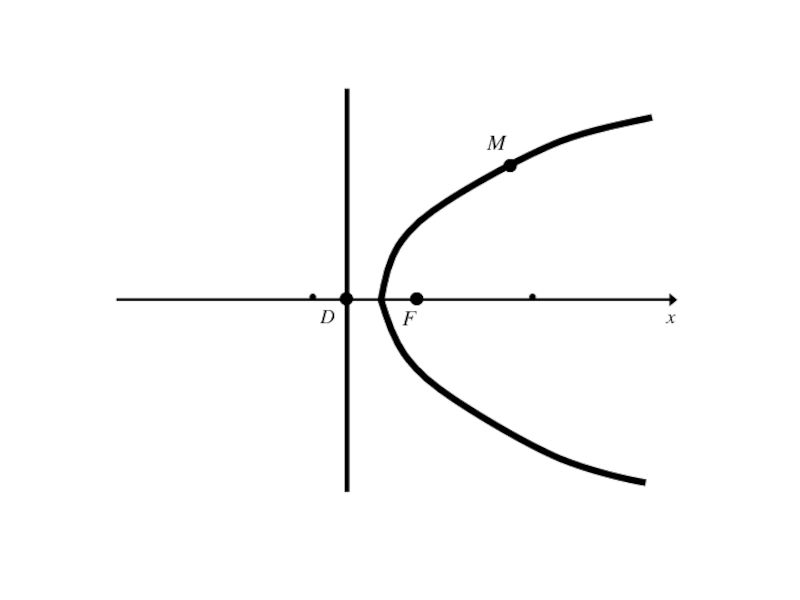
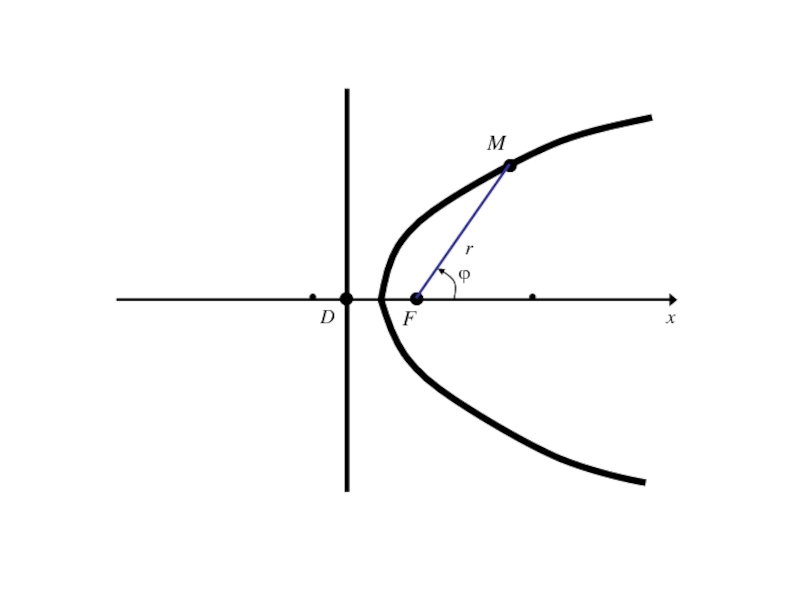
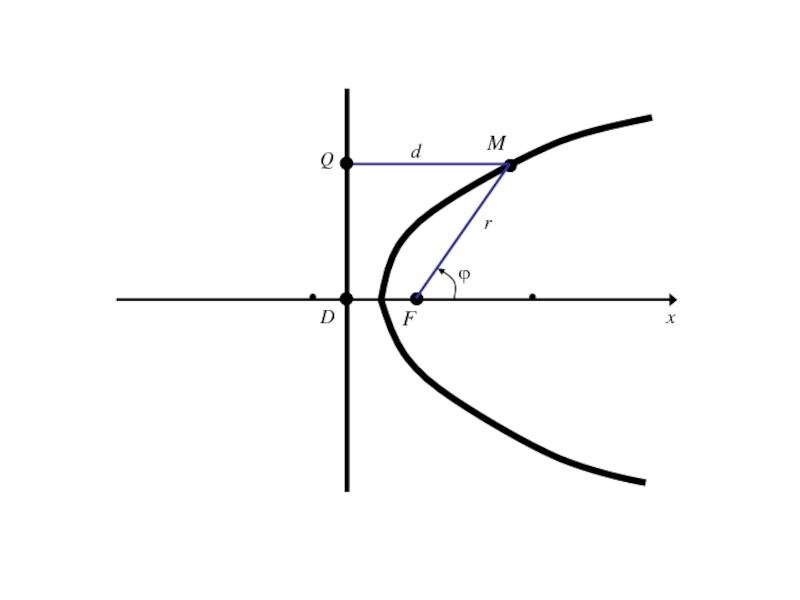
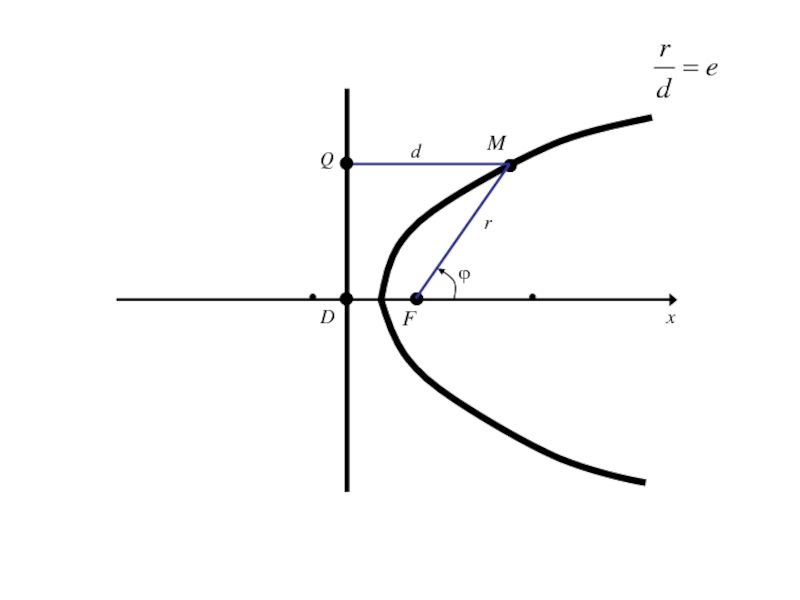
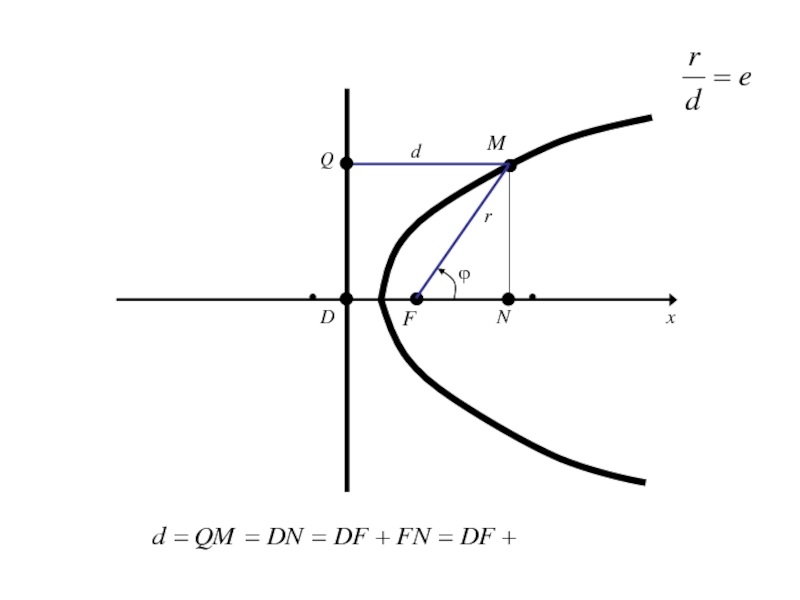
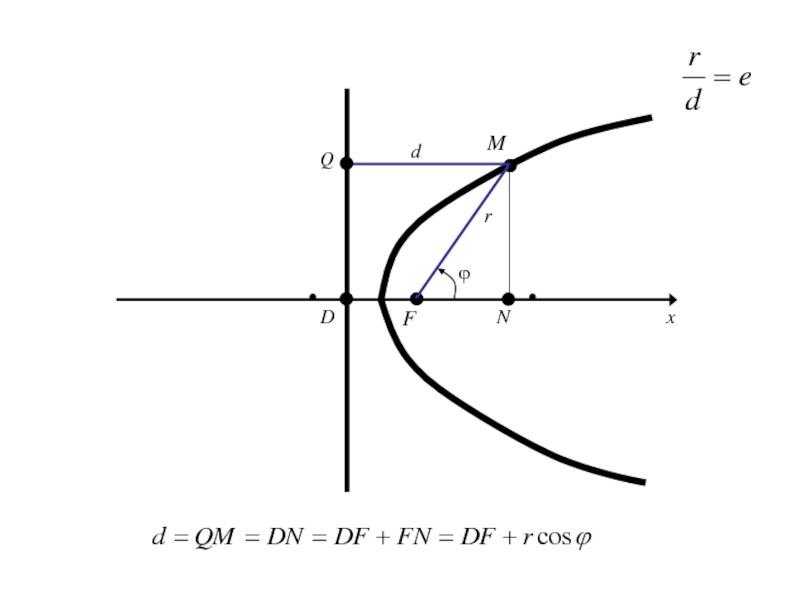
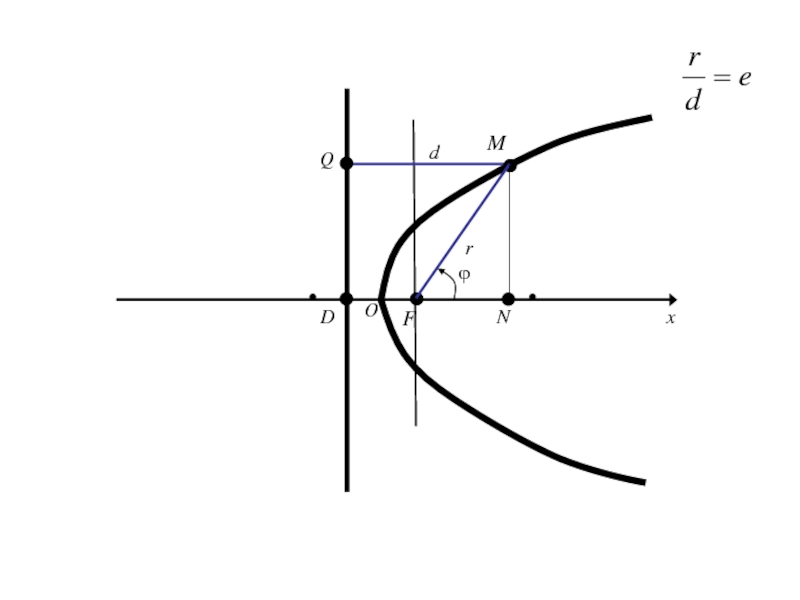
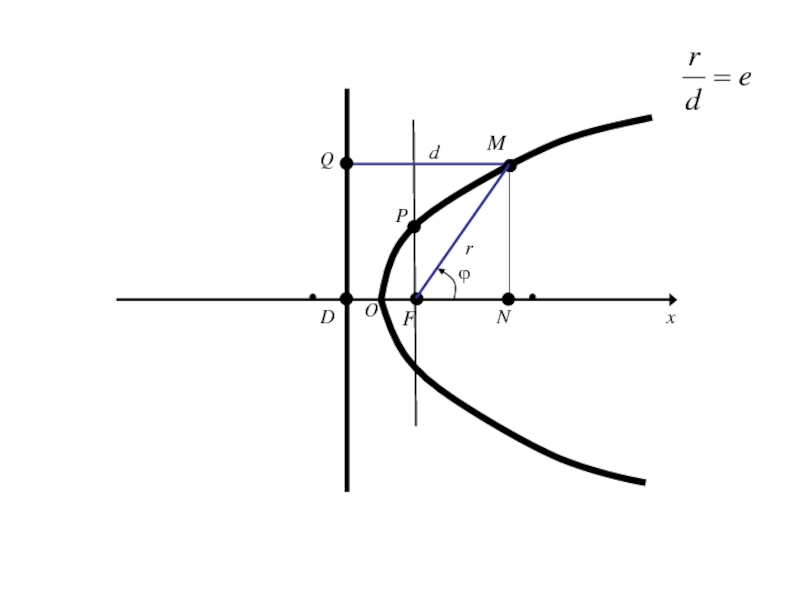
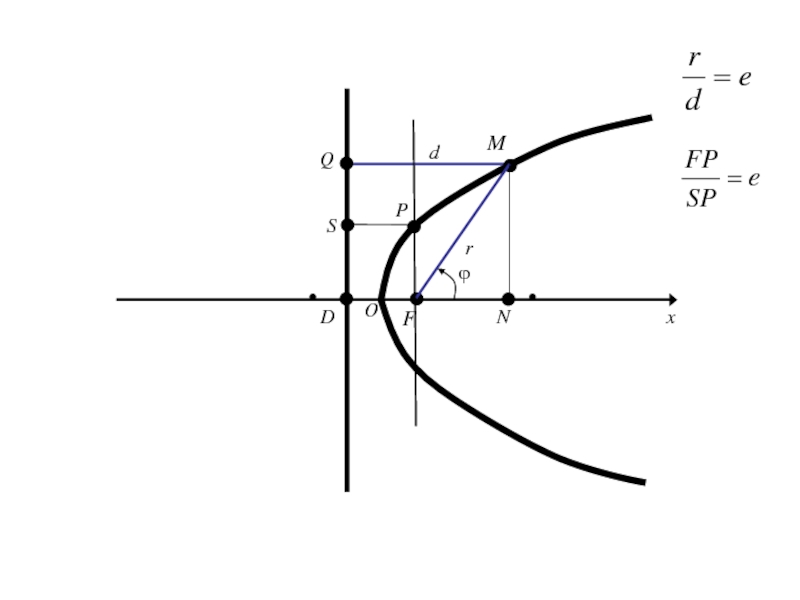
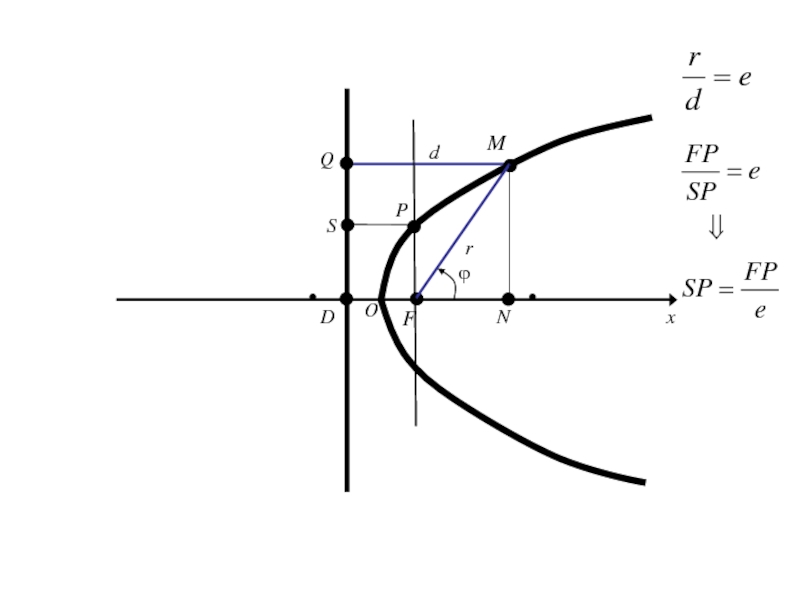
- 313. OxyF
- 314. Слайд 314
- 315. Слайд 315
- 316. Слайд 316
- 317. Слайд 317
- 318. Самостоятельно изучить вопросы по данной теме:Уравнение касательной к параболеОптическое свойство параболы
- 319. 9.Уравнение эллипса, параболы и гиперболы в полярных координатах.
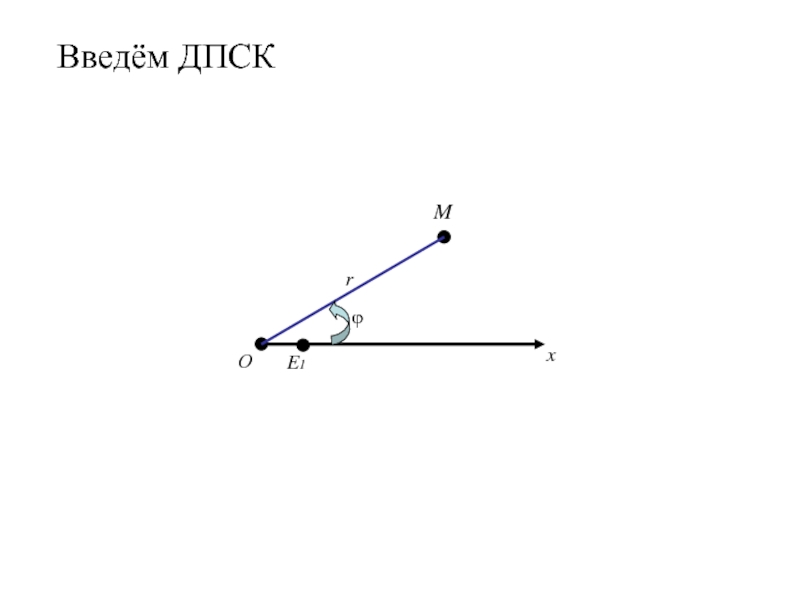
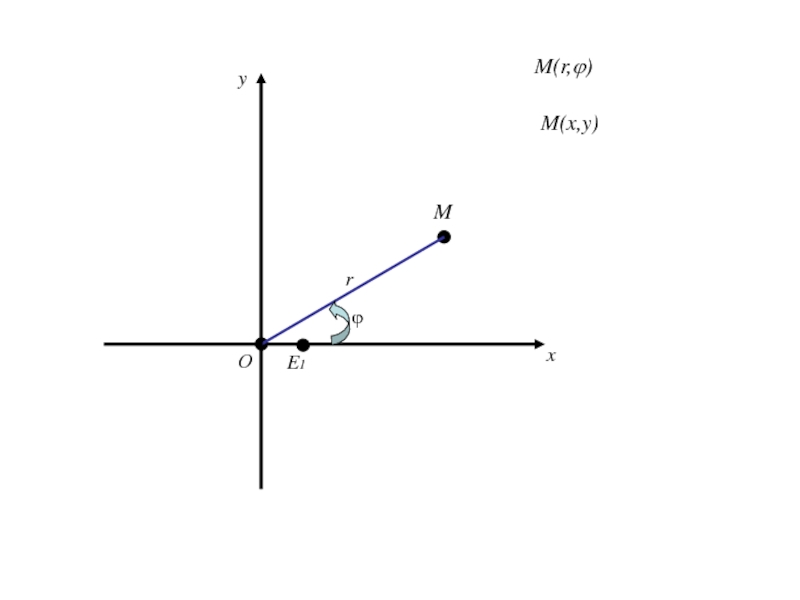
- 320. Полярная система координат на плоскости. Говорят, что
- 321. О
- 322. Оx
- 323. ОxE1
- 324. ОxE1M
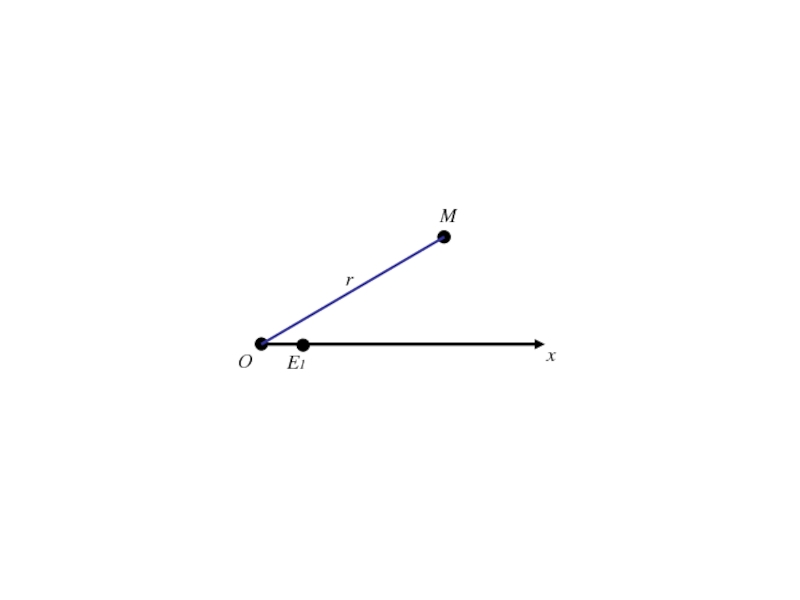
- 325. ОxE1Mr
- 326. ОxE1Mrполярный радиус М
- 327. ОxE1Mrполярный радиус Мϕ
- 328. ОxE1Mr
- 329. ОxE1r ϕM(r,ϕ)
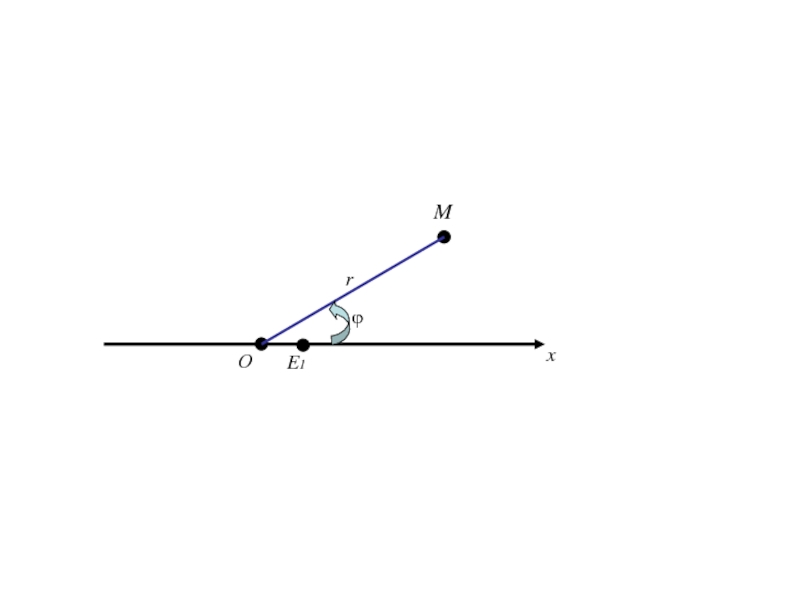
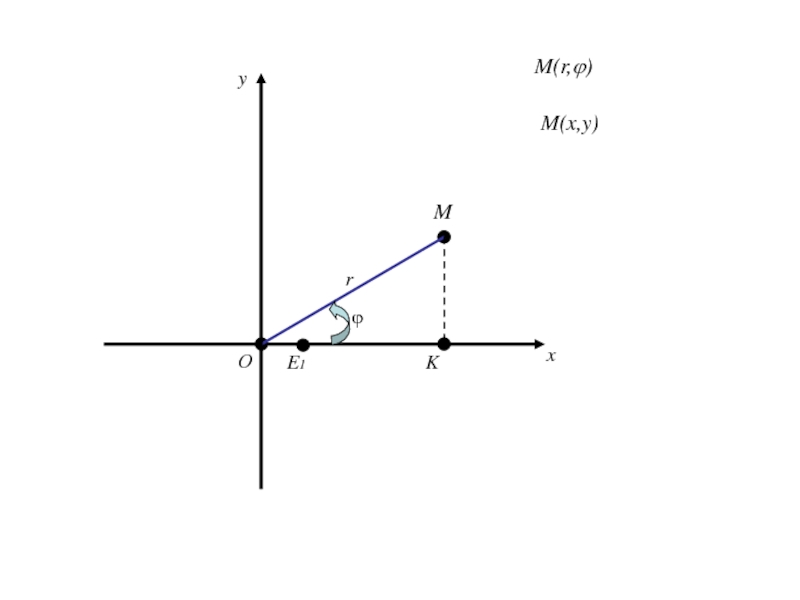
- 330. ОxE1r Введём ДПСК ϕM
- 331. ОxE1r ϕM
- 332. ОxE1r ϕMy
- 333. ОxE1r ϕMyM(r,ϕ)
- 334. ОxE1r ϕMyM(x,y)M(r,ϕ)
- 335. ОxE1r ϕMyM(x,y)M(r,ϕ)K
- 336. ОxE1r ϕMyM(x,y)M(r,ϕ)K
- 337. ОxE1r ϕMyM(x,y)M(r,ϕ)K
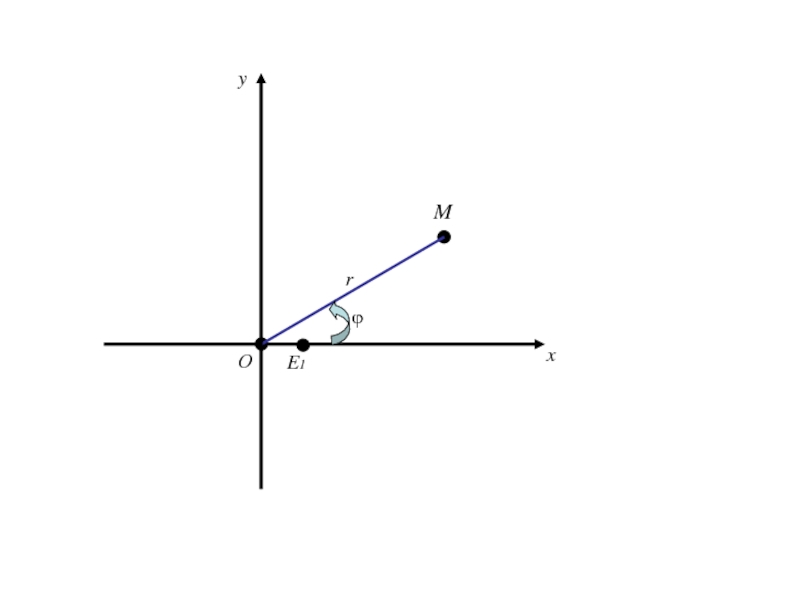
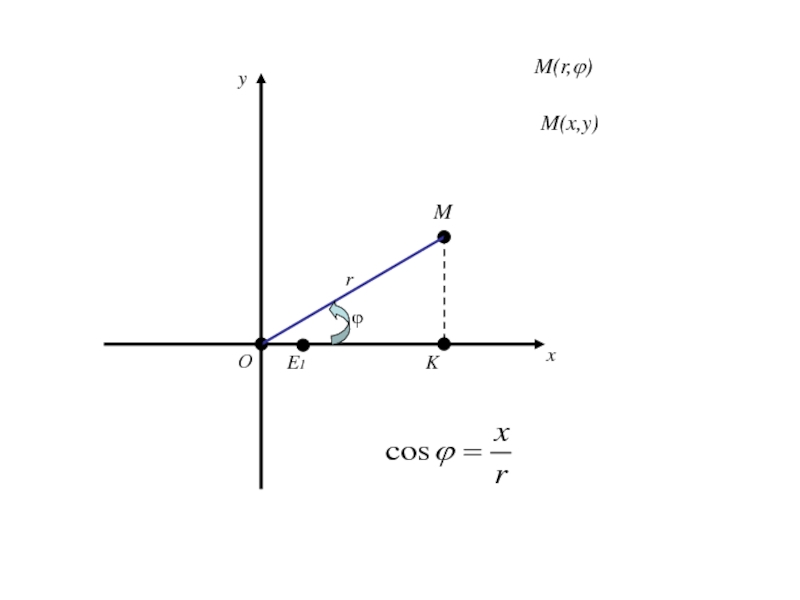
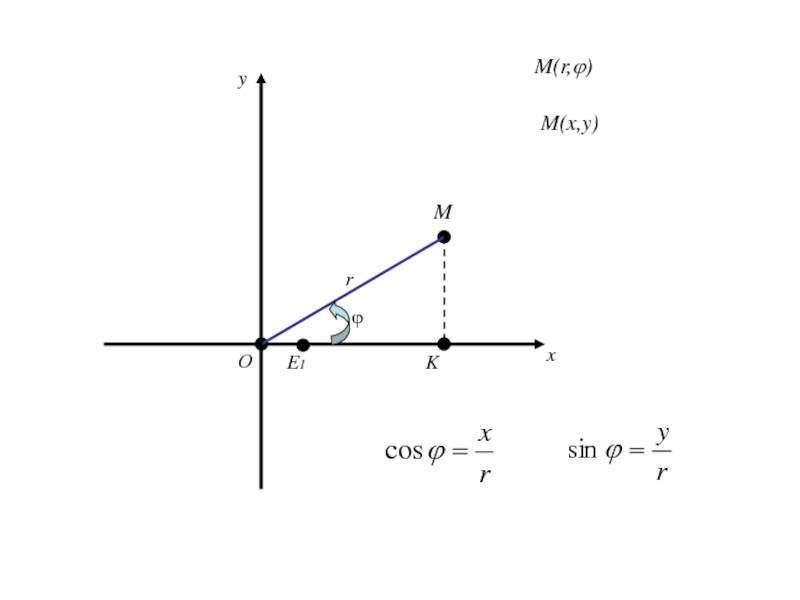
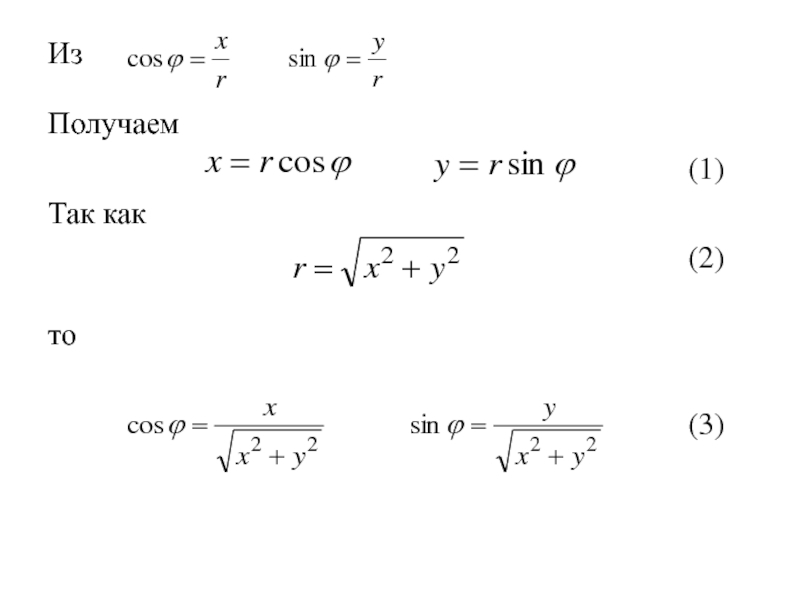
- 338. Из Получаем (1)
- 339. Из Получаем (1)Так как (2)
- 340. Из Получаем (1)Так как (2)то (3)
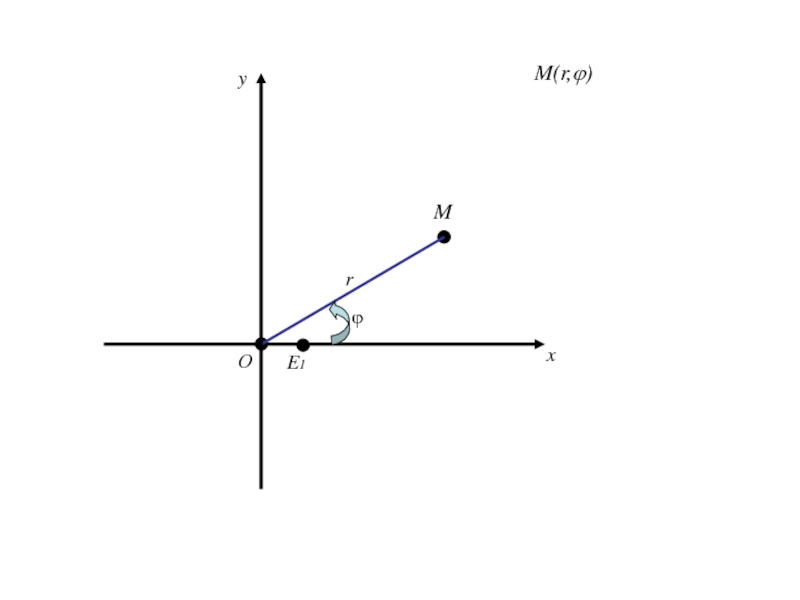
- 341. Формулы (1) позволяют вычислить декартовые прямоугольные координаты х, у точки М по её полярным координатам ϕ,r.
- 342. Формулы (1) позволяют вычислить декартовые прямоугольные координаты
- 343. Полярное уравнение эллипса, гиперболы и параболы Пусть
- 344. Полярное уравнение эллипса, гиперболы и параболы Пусть
- 345. Введем полярную систему координат, совмещая полюс с
- 346. Пусть D-основание перпендикуляра, опущенного из F на
- 347. MFDx
- 348. MFDxrϕ
- 349. MFDxrdQϕ
- 350. MFDxrdQϕ
- 351. MFDxrdQϕN
- 352. MFDxrdQϕN
- 353. MFDOxrdQNϕ
- 354. MFDOxPrdQNϕ
- 355. MFDOxPrdSQNϕ
- 356. MFDOxPrdSQNϕ
- 357. Половина длины фокальной хорды (т. е. хорды,
- 358. Половина длины фокальной хорды (т. е. хорды,
- 359. Половина длины фокальной хорды (т. е. хорды,
- 360. Половина длины фокальной хорды (т. е. хорды,
- 361. Половина длины фокальной хорды (т. е. хорды,
- 362. Половина длины фокальной хорды (т. е. хорды,
- 363. Половина длины фокальной хорды (т. е. хорды,
- 364. Половина длины фокальной хорды (т. е. хорды,
- 365. Слайд 365
- 366. Полярное уравнение кривой 2-го порядка
- 367. Слайд 367
- 368. ВСЁ
- 369. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Содержание
1. Эллипс и его каноническое уравнение.
4. Гипербола и её
каноническое уравнение
гиперболы и параболыСлайд 3Взять в библиотеке методичку:
КРИВЫЕ ВТОРОГО ПОРЯДКА:
АДАПТИВНО-МОДУЛЬНАЯ ТЕХНОЛОГИЯ
Методические рекомендации
для самостоятельной работы
студентов
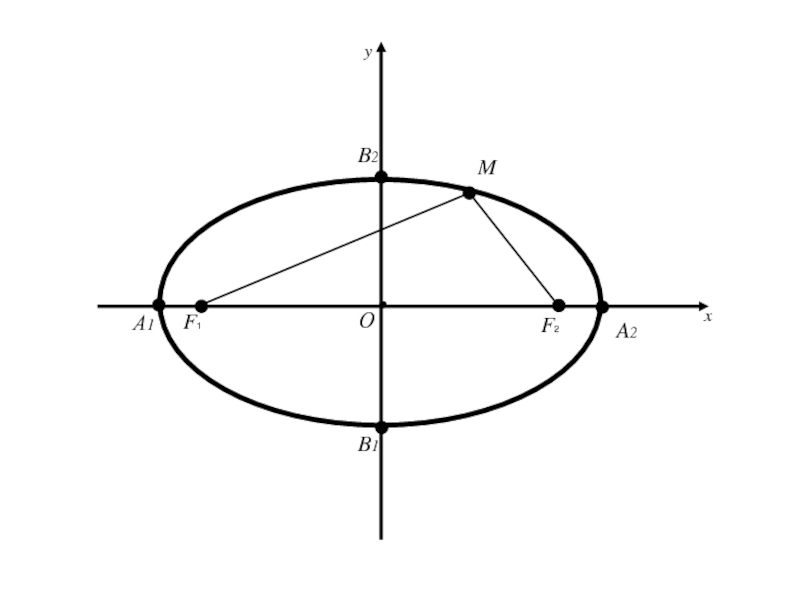
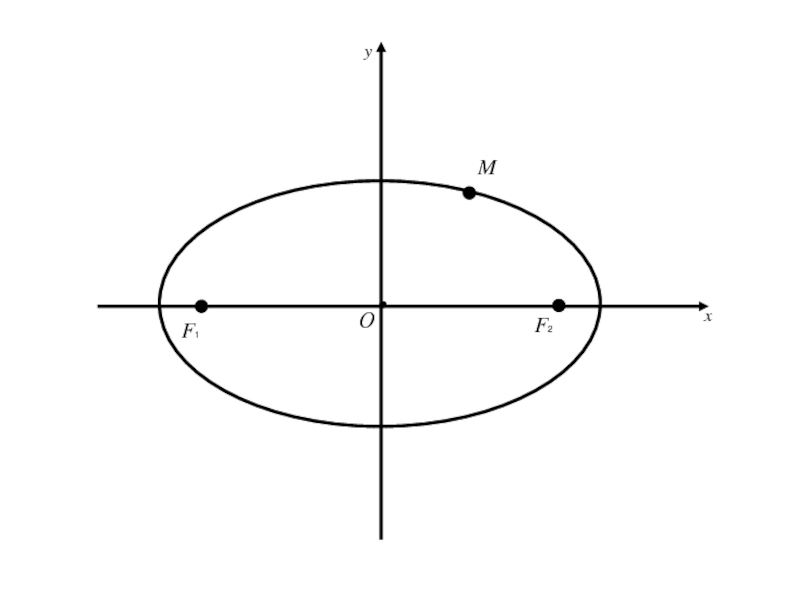
Слайд 41. Эллипс и его каноническое уравнение
Эллипсом называется геометрическое место точек
плоскости, для каждой из которых сумма расстояний до двух фиксированных
точек плоскости, называемых фокусами, есть величина постоянная, равная 2a , большая, чем расстояние между фокусами, равное 2c.Слайд 18Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
Слайд 19Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогдаСлайд 20Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогда
Слайд 37
Таким образом, мы доказали, что координаты любой точки M (x;
y) эллипса удовлетворяют уравнению (2).
Слайд 38
Таким образом, мы доказали, что координаты любой точки M (x;
y) эллипса удовлетворяют уравнению (2). Однако это уравнение пока нельзя
назвать уравнением эллипса, т.к. не доказано обратное предположение:Слайд 39Если числа x и y удовлетворяют уравнению (2), то точка
M (x; y) удовлетворяет соотношению (1), т.е. лежит на эллипсе.
Слайд 40Если числа x и y удовлетворяют уравнению (2), то точка
M (x; y) удовлетворяет соотношению (1), т.е. лежит на эллипсе.
Слайд 54Таким образом, уравнение (2) есть уравнение эллипса, т.к. доказано, что
координаты любой точки M (x; y) эллипса, т.е. любой точки,
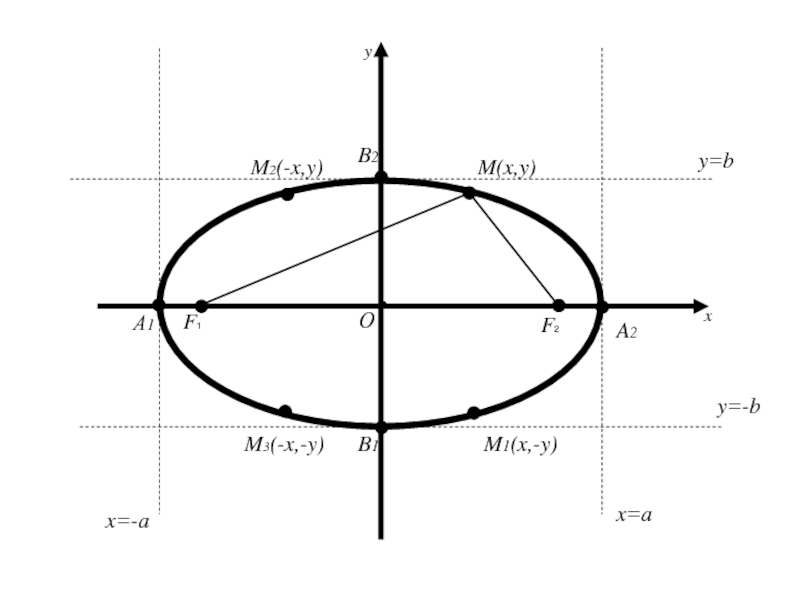
для которой выполняется выражение (1) удовлетворяет уравнению (2) и обратно, если два числа x и y удовлетворяет уравнению (2), то точка M (x; y) удовлетворяет соотношению (1), т.е. лежит на эллипсе.Слайд 572. Исследование формы эллипса.
Так как координаты x и y
входят в уравнение в четной степени, то если на эллипсе
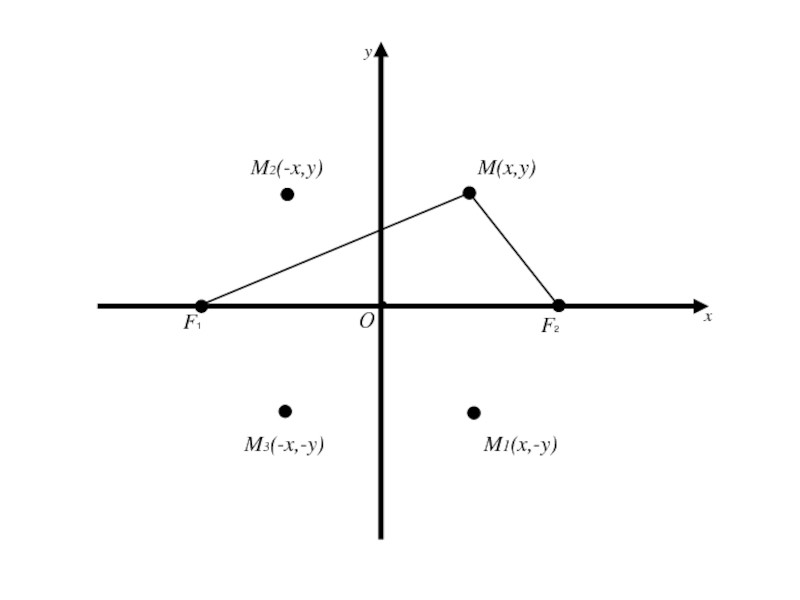
лежит любая точка M(x, y) ( т.е. координаты этой точки удовлетворяют уравнению(2)),Слайд 582. Исследование формы эллипса.
Так как координаты x и y
входят в уравнение в четной степени, то если на эллипсе
лежит любая точка M(x, y) ( т.е. координаты этой точки удовлетворяют уравнению(2)), то на этом эллипсе будут лежать точки M1(-x,y) и M2(x, -y), симметричные с точкой M(x, y) относительно осей Ox и Oy и точка M3(-x;-y), cимметричная относительно начала координат.Слайд 592. Исследование формы эллипса.
Так как координаты x и y
входят в уравнение в четной степени, то если на эллипсе
лежит любая точка M(x, y) ( т.е. координаты этой точки удовлетворяют уравнению(2)), то на этом эллипсе будут лежать точки M1(-x,y) и M2(x, -y), симметричные с точкой M(x, y) относительно осей Ox и Oy и точка M3(-x;-y), cимметричная относительно начала координат.Следовательно, оси Ox и Oy являются осями симметрии, а начало координат – центром симметрии эллипса.
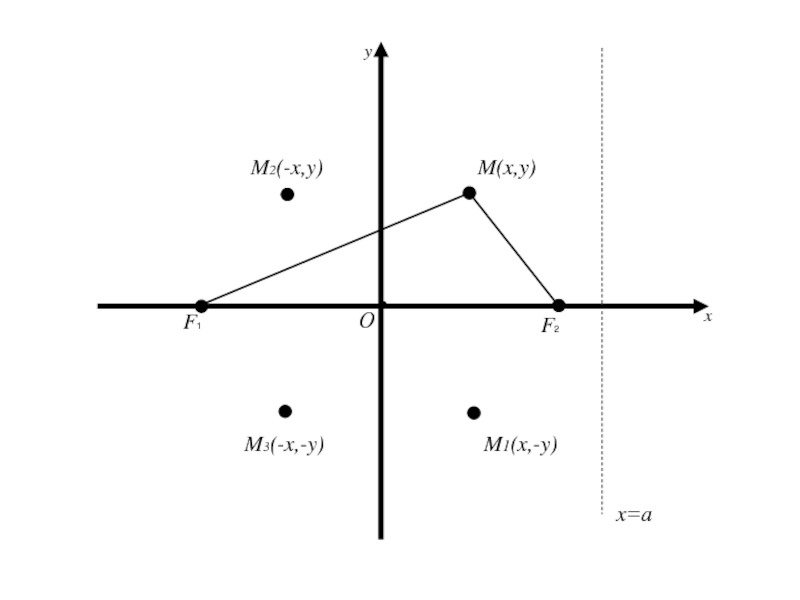
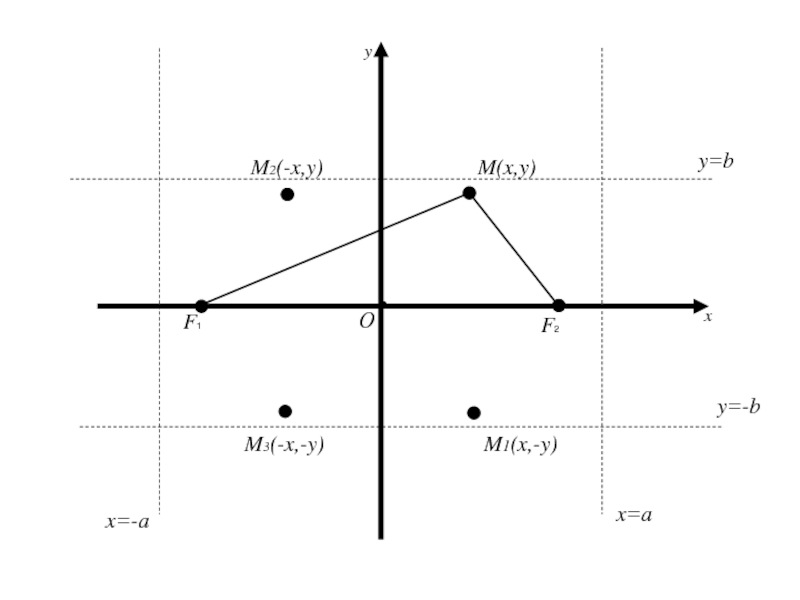
Слайд 61Следует, что для координат любой точки имеет место
Геометрически это
означает, что эллипс расположен внутри прямоугольника, сторонами которого являются прямые
x=a, x=-a, y=b, y=-b
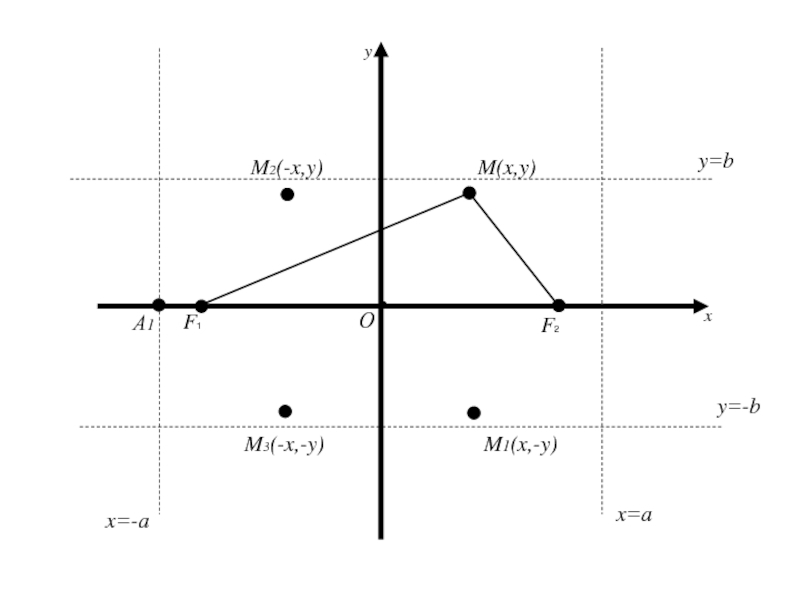
Слайд 77Точки пересечения эллипса с осями координат называются вершинами эллипса
Полуосью
эллипса называется отрезок, одним концом которого является центр симметрии эллипса,
а другим одна из его вершин.Слайд 78Точки пересечения эллипса с осями координат называются вершинами эллипса
Полуосью
эллипса называется отрезок, одним концом которого является центр симметрии эллипса,
а другим одна из его вершин.Будем предполагать, что в каноническом уравнении (2) a>b, тогда
a – большая полуось
b – меньшая полуось
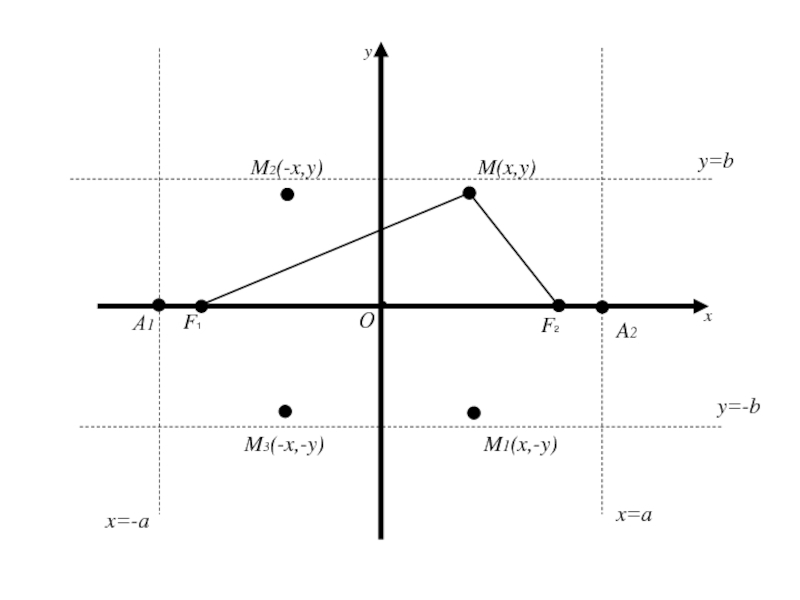
Слайд 79Точки пересечения эллипса с осями координат называются вершинами эллипса
Полуосью
эллипса называется отрезок, одним концом которого является центр симметрии эллипса,
а другим одна из его вершин.Будем предполагать, что в каноническом уравнении (2) a>b, тогда
a – большая полуось
b – меньшая полуось
В случае a=b уравнение (2) примет вид
Слайд 80Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей
полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:
Слайд 81Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей
полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:
Слайд 82Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей
полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:
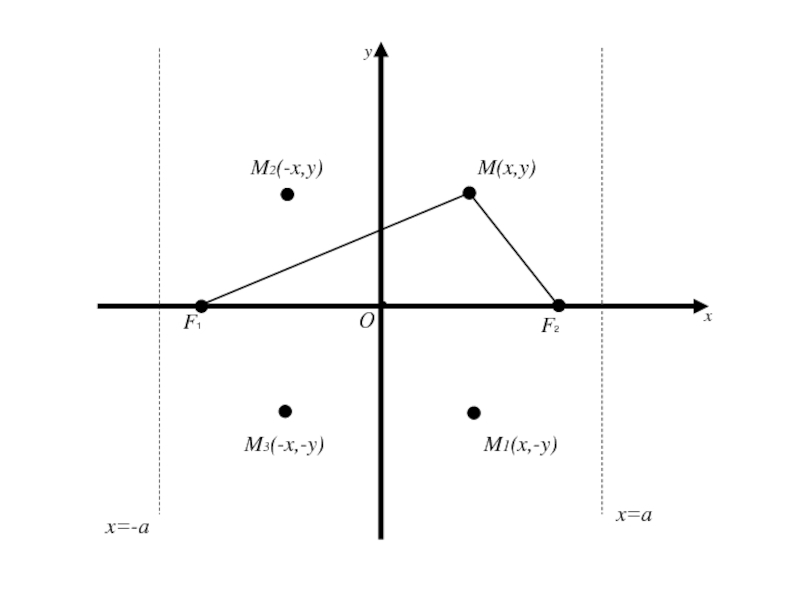
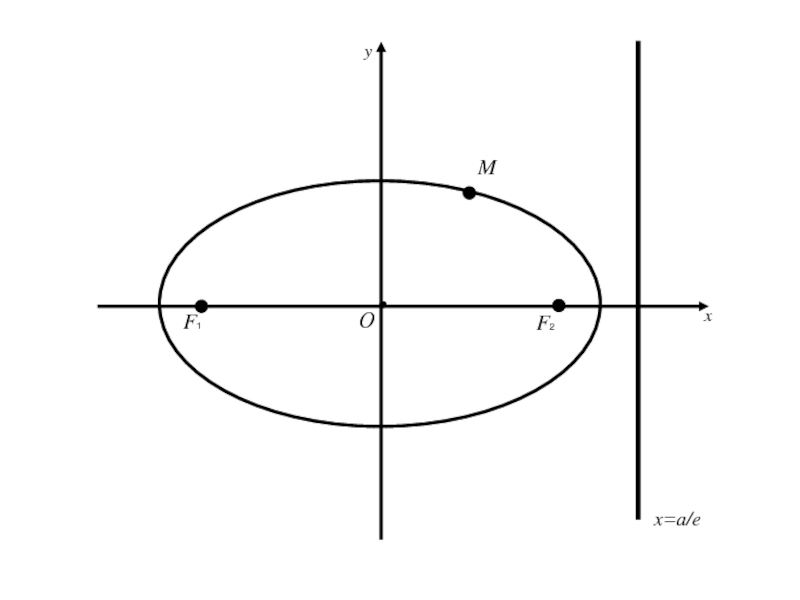
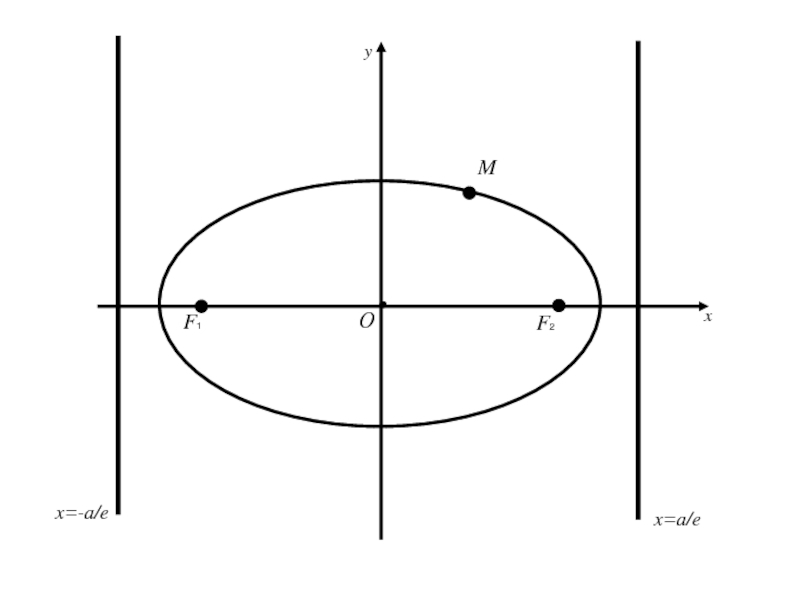
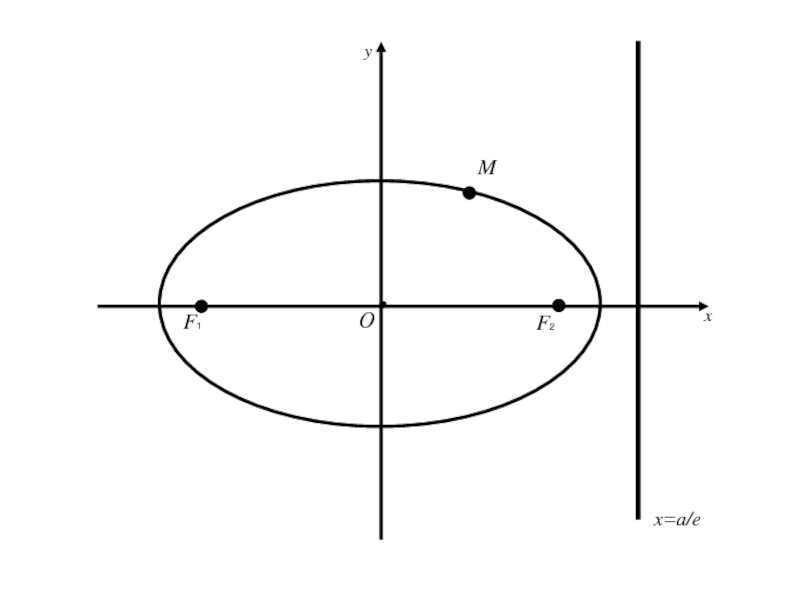
Слайд 833.Директрисы эллипса.
Две прямые перпендикулярные оси эллипса, на которой расположены его
фокусы, и отстоящие от центра эллипса на расстояние a/e, где
a –большая полуось эллипса, e –эксцентриситет называются директрисами эллипса.
Слайд 843.Директрисы эллипса.
Две прямые перпендикулярные оси эллипса, на которой расположены его
фокусы, и отстоящие от центра эллипса на расстояние a/e, где
a –большая полуось эллипса, e –эксцентриситет называются директрисами эллипса.Уравнения директрис имеют вид
Слайд 88Теорема: Для того, чтобы точка лежала на эллипсе необходимо и достаточно,
чтобы отношение расстояния от этой точки до фокуса эллипса к
расстоянию от той же точки до директрисы, соответствующей рассматриваемому фокусу, было равно эксцентриситету эллипса.Слайд 100 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
Слайд 101 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 102 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 103 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 104 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 105 (=>) имеем точку M(x;y) принадлежащую эллипсу (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 106 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)(<=)
Слайд 107 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
(<=)
Слайд 108 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
(<=)
Слайд 109 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
(<=)
Слайд 110 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
Возведём в квадрат, упростим, помня, что
(<=)
Слайд 111 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит эллипсу,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
Возведём в квадрат, упростим, помня, что
получим
(<=)
Слайд 112Самостоятельно изучить вопросы
по данной теме:
Вид эллипса в случае a
касательной к эллипсу
Оптическое свойство эллипса
Слайд 1134. Гипербола и её каноническое уравнение
Гиперболой называется геометрическое место точек,
для каждой из которых абсолютная величина разности расстояний до двух
фиксированных точек плоскости, называемых фокусами, есть данное положительное число 2a меньшее, чем расстояние 2c между фокусами.Слайд 128Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
Слайд 129Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогдаСлайд 130Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогда
Слайд 135По определению |F1М - F2М | = 2a (1)
Получим
избавимся
от модуля и преобразуем
возведём обе части в квадрат
Слайд 136По определению |F1М - F2М | = 2a (1)
Получим
избавимся
от модуля и преобразуем
возведём обе части в квадрат
Слайд 137По определению |F1М - F2М | = 2a (1)
Получим
избавимся
от модуля и преобразуем
возведём обе части в квадрат
Слайд 150
Докажем обратное: если координаты некоторой точки М(x,y) удовлетворяют уравнению (2),
то для этой точки выполнятся равенство |F1М - F2 М
| = 2a (1)
Слайд 165Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Слайд 166Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Слайд 167Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Если
Слайд 168Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Если или
Слайд 169Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Если или , то
Слайд 175Таким образом, получаем
если
если
Подставим в равенство
(|F1М - F2 М | = 2a)
если выполняется
Слайд 176Таким образом, получаем
если
если
Подставим в равенство
(|F1М - F2 М | = 2a)
если выполняется
если , то
Слайд 177Таким образом, получаем
если
если
Подставим в равенство
(|F1М - F2 М | = 2a)
если выполняется
если , то
Слайд 178Таким образом, уравнение (2) есть уравнение гиперболы, т.к. доказано, что
координаты любой точки M (x; y) гиперболы, т.е. любой точки,
для которой выполняется выражение (1) удовлетворяет уравнению (2) и обратно, если два числа x и y удовлетворяет уравнению (2), то точка M (x; y) удовлетворяет соотношению (1), т.е. лежит на гиперболе.Слайд 182 5. Исследование формы гиперболы
Т.к. в каноническое уравнение гиперболы координаты x
и y входят во второй степени
Слайд 183 5. Исследование формы гиперболы
Т.к. в каноническое уравнение гиперболы координаты x
и y входят во второй степени => оси Ox и
Oy являются осями симметрии гиперболы, а начало координат центром симметрии.Слайд 184Из уравнения => что
,т.е. и
Геометрически это означает, что между прямыми x=a и x=-a нет точек гиперболы.
Слайд 185Из уравнения => что
,т.е. и
Геометрически это означает, что между прямыми x=a и x=-a нет точек гиперболы.
Ось симметрии Oy не пересекает гиперболу и называется мнимой осью.
Слайд 186Ось симметрии Ox пересекает гиперболу в двух точках A1(-a;0) A2(a;0)
– вершинах гиперболы и называется действительной осью.
Слайд 187Ось симметрии Ox пересекает гиперболу в двух точках A1(-a;0) A2(a;0)
– вершинах гиперболы и называется действительной осью.
a и b
в уравнении гиперболы называются соответственно действительной и мнимой полуосями гиперболы.Слайд 189Выразим y из уравнения гиперболы и возьмем положительное значение
считая,
что получим точки
гиперболы, лежащие в I четверти.
Слайд 190Выразим y из уравнения гиперболы и возьмем положительное значение
считая,
что получим точки
гиперболы, лежащие в I четверти.Из уравнения (3) => что y в полуинтервале есть возрастающая функция при этом предел
Слайд 191Выразим y из уравнения гиперболы и возьмем положительное значение
считая,
что получим точки
гиперболы, лежащие в I четверти.Из уравнения (3) => что y в полуинтервале есть возрастающая функция при этом предел
Слайд 192Выразим y из уравнения гиперболы и возьмем положительное значение
считая,
что получим точки
гиперболы, лежащие в I четверти.Из уравнения (3) => что y в полуинтервале есть возрастающая функция при этом предел
Слайд 193Всякая прямая пересекает гиперболу не более чем в двух точках,
так как прямая определяется уравнением I степени, а гипербола -
II
Слайд 194Рассмотрим уравнение прямой
или
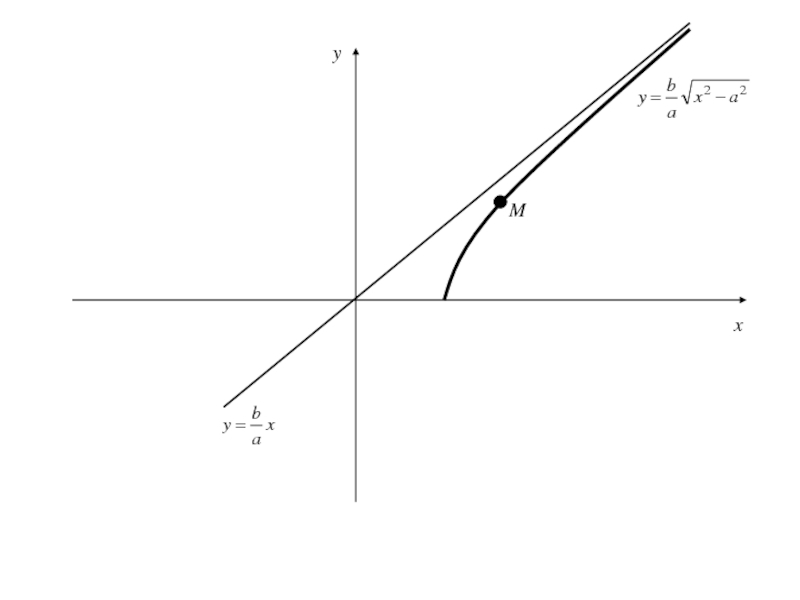
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
Слайд 195Рассмотрим уравнение прямой
или
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
Слайд 196Рассмотрим уравнение прямой
или
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
Слайд 197Рассмотрим уравнение прямой
или
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
Слайд 198Рассмотрим уравнение прямой
или
Найдем расстояние d от точки M(x,y), лежащей на
дуге гиперболы, определенной уравнением (3), до прямой (4):
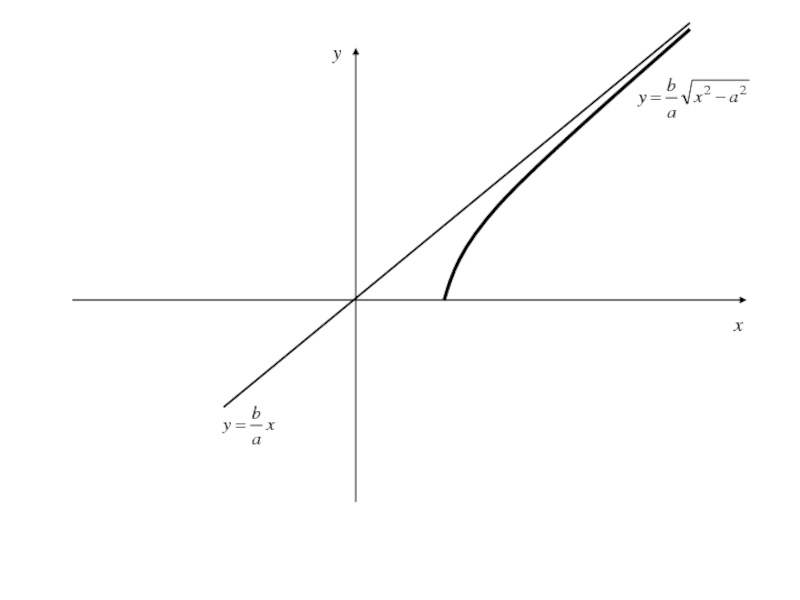
Слайд 199Получили, что на полуинтервале
расстояние d от точки M(x,y) рассматриваемой части гиперболы до
прямой (4) есть убывающая функция и(т.е. расстояние стремиться к 0)
Слайд 200Получили, что на полуинтервале
расстояние d от точки M(x,y) рассматриваемой части гиперболы до
прямой (4) есть убывающая функция и(т.е. расстояние стремиться к 0)
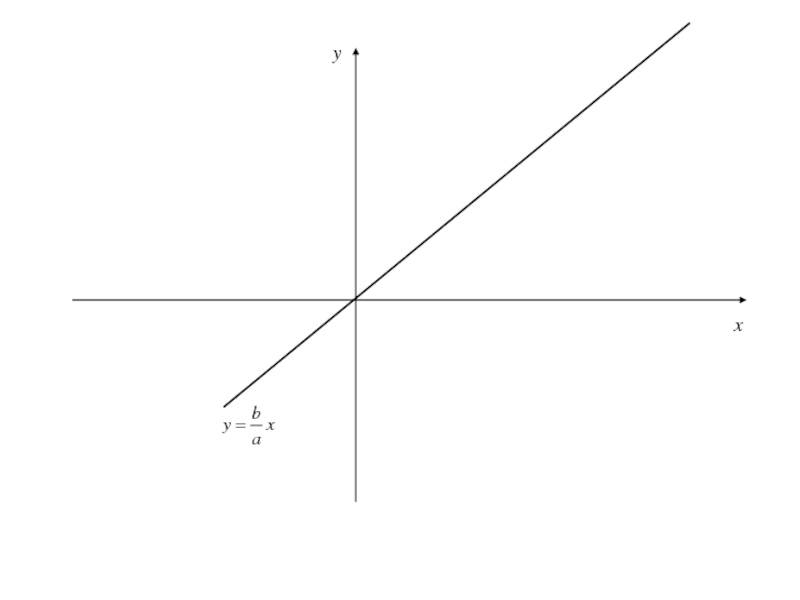
Прямая, определяемая уравнением называется асимптотой гиперболы.
Слайд 206В силу того, что гипербола, заданная каноническим уравнением, симметрична относительно
начала координат, расстояние от точки М(x;y), лежащей на дуге гиперболы,
заданой
уравнением до прямой
стремится к нулю при
Слайд 207Так как гипербола, заданная каноническим уравнением, симметрична относительно оси Оy,
то она имеет вторую асимптоту
которая обладает свойством аналогичным свойству первой
асимптоты по отношению к дугам гиперболы, расположенной в II и IV четвертях .Асимптоты являются диагоналями прямоугольника с вершинами Р(а;b), Q(-a;b), S(a;-b), K(-a;-b).
Слайд 2176. Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы
до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и
обозначается буквой еСлайд 2186. Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы
до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и
обозначается буквой е
Слайд 2196. Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы
до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и
обозначается буквой еТак как для гиперболы 0 < а < с, то е >1
Слайд 222Две прямые, перпендикулярные действительной оси гиперболы и отстоящие от центра
гиперболы на расстояние а/е (где a – действительная полуось, е
– эксцентриситет гиперболы), называются директрисами гиперболыСлайд 224Для гиперболы, заданной каноническим уравнением
уравнения директрис имеют вид
Т.к. e
>1, то директрисы отстоят от центра на расстоянии меньшем действительной
полуоси.
Слайд 227Теорема: Для того чтобы точка лежала на гиперболе, необходимо и
достаточно, чтобы
отношение расстояния от этой точки до фокуса гиперболы
к расстоянию от той же точки до директрисы, соответствующей рассматриваемому фокусу, было равно эксцентриситету гиперболы.Слайд 233 (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой
выполняется
требуется доказать, что
Слайд 234 (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой
выполняется
требуется доказать, что
Найдём
Слайд 235 (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 236 (=>) имеем точку M(x;y) принадлежащую гиперболе (2), для которой
выполняется
требуется доказать, что
найдём
Слайд 237 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур.(2)(<=)
Слайд 238 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
(<=)
Слайд 239 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
(<=)
Слайд 240 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
(<=)
Слайд 241 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
Возведём в квадрат, упростим, помня, что
(<=)
Слайд 242 Пусть существует точка M(x;y), для которой
выполняется докажем, что точка принадлежит гиперболе,
т.е. её координаты удовлетворяют ур. (2)Так как F2 (c,0), тогда
из
Подставим
Возведём в квадрат, упростим, помня, что
получим
(<=)
Слайд 243Самостоятельно изучить вопросы по данной теме:
Понятие сопряженной гиперболы
Уравнение касательной к
гиперболе
Оптическое свойство гиперболы
Слайд 2447. Парабола и её каноническое уравнение
Параболой называется геометрическое место
точек, для каждой из которых расстояние до некоторой фиксированной точки
плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, не проходящей через фокус, и называемой директрисой.Слайд 2457. Парабола и её каноническое уравнение
Расстояние от фокуса параболы
до её директрисы называется параметром параболы.
Слайд 2467. Парабола и её каноническое уравнение
Расстояние от фокуса параболы
до её директрисы называется параметром параболы.
Эксцентриситет параболы принимается равным 1
Слайд 255Расстояние FD обозначим р (параметр параболы).
тогда в выбранной системе координат
фокус F будет иметь координаты
Слайд 256Расстояние FD обозначим р (параметр параболы).
тогда в выбранной системе координат
фокус F будет иметь координаты F( ;0)
Слайд 257Расстояние FD обозначим р (параметр параболы).
тогда в выбранной системе координат
фокус F будет иметь координаты F( ;0)
а уравнение
директрисы
Слайд 258Расстояние FD обозначим р (параметр параболы).
тогда в выбранной системе координат
фокус F будет иметь координаты F( ;0)
а уравнение
директрисы x=-
Слайд 267Точка M(x;y) лежит на данной параболе тогда и только тогда,
когда r = d
r=|FM|=
d=|PM|=
То уравнение параболы примет вид
Слайд 2748. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то
Слайд 2758. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то ось Ox является осью симметрии
параболы (1).Слайд 2768. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то ось Ox является осью симметрии
параболы (1).Точка пересечения параболы с её осью симметрии называется вершиной параболы.
Слайд 2778. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то ось Ox является осью симметрии
параболы (1).Точка пересечения параболы с её осью симметрии называется вершиной параболы.
Имеет только одну вершину в точке
Слайд 2788. Исследование формы параболы
Т.к. ордината у в каноническом уравнении параболы
входит во 2-й степени, то ось Ox является осью симметрии
параболы (1).Точка пересечения параболы с её осью симметрии называется вершиной параболы.
Имеет только одну вершину в точке О(0;0).
Слайд 2808. Исследование формы параболы
Всякая прямая пересекает параболу не более чем
в двух точках (т.к. прямая определяется уравнением 1-ой степени, а
парабола - уравнением 2-ой степени)Слайд 284Из (1) ⇒, что x≥0 (т. к. p>0, а
Разрешая уравнение (1) относительно
у и беря лишь неотрицательные значения Слайд 285Из (1) ⇒, что x≥0 (т. к. p>0, а
Разрешая уравнение (1) относительно
у и беря лишь неотрицательные значения видим, что в полуинтервале [0;+∞),
Слайд 286Из (1) ⇒, что x≥0 (т. к. p>0, а
Разрешая уравнение (1) относительно
у и беря лишь неотрицательные значения видим, что в полуинтервале [0;+∞),
y - возрастающая функция, причем
Слайд 287Из (1) ⇒, что x≥0 (т. к. p>0, а
Разрешая уравнение (1) относительно
у и беря лишь неотрицательные значения видим, что в полуинтервале [0;+∞),
y - возрастающая функция, причем
Слайд 293Уравнение
, где р>0,
сводиться к
уравнению (1) заменой x на −x, т. е. путём преобразования системы координат, которая соответствует изменению положительного направления оси Ox на противоположное.
Слайд 294Уравнение
, где р>0,
сводиться к
уравнению (1) заменой x на −x, т. е. путём преобразования системы координат, которая соответствует изменению положительного направления оси Ox на противоположное.
Отсюда следует, что парабола
симметрична с параболой
относительно оси Oy
Слайд 303Аналогичными рассуждениями устанавливаем, что каждое из уравнений
где p>0
определяет
параболу с вершиной в начале координат и осью симметрии Oy
Слайд 318Самостоятельно изучить вопросы по данной теме:
Уравнение касательной к параболе
Оптическое свойство
параболы
Слайд 320Полярная система координат на плоскости.
Говорят, что на плоскости введена
полярная система координат, если эта плоскость ориентирована, на ней выбраны
точка О – полюс, луч Ох, выходящий из точки О - полярная ось и масштабный отрезок.Слайд 341Формулы (1) позволяют вычислить декартовые прямоугольные координаты х, у точки
М по её полярным координатам ϕ,r.
Слайд 342Формулы (1) позволяют вычислить декартовые прямоугольные координаты х, у точки
М по её полярным координатам ϕ,r.
Формулы (2) и (3) позволяют
вычислить полярные координаты ϕ и r, по её декартовым координатам х, у .Слайд 343Полярное уравнение эллипса, гиперболы и параболы
Пусть L-какая-нибудь из изученных
нами линий второго порядка,
(если L-гипербола, то имеем в виду
одну из её ветвей). Слайд 344Полярное уравнение эллипса, гиперболы и параболы
Пусть L-какая-нибудь из изученных
нами линий второго порядка,
(если L-гипербола, то имеем в виду
одну из её ветвей). Будем называть фокальной осью линии L, ту из её осей симметрии, которая проходит через фокус этой линии.
Слайд 345Введем полярную систему координат, совмещая полюс с фокусом F (в
случае гиперболы берем фокус ближайший к вершине рассматриваемой ветви).
Слайд 346Пусть D-основание перпендикуляра, опущенного из F на директрису, соответствующего этому
фокусу. Полярную ось расположим на прямой DF, причем положительное направление
примем от D к F.Слайд 357Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Слайд 358Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
Слайд 359Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
Слайд 360Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вСлайд 361Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вВыразим r:
Слайд 362Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вВыразим r:
Слайд 363Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вВыразим r:
Слайд 364Половина длины фокальной хорды (т. е. хорды, проходящей через фокус
перпендикулярно к фокальной оси) называется фокальным параметром (p).
Тогда
подставим вВыразим r: