Слайд 2Доля кинематики в ЕГЭ.
В экзаменационной работе
по КИНЕМАТИКЕ включены следующие основные темы:
Механическое движение и его относительность
Скорость
Ускорение
Прямолинейное
равноускоренное движение
Свободное падение (ускорение свободного падения)
Движение по окружности с постоянной по модулю скоростью
Центростремительное ускорение
Равномерное движение
Слайд 3Доля кинематики в ЕГЭ.
В экзамене КИНЕМАТИКА представлена в малом количестве,
но в комбинированных задачах эта тема присутствует достаточно .
Задача
школьного учителя не только знакомить детей со всеми темами данного раздела, но и развивать у них экспериментальные и общие учебные информационные умения.
Слайд 4Общие учебные информационные умения
Активное чтение(восприятие) материала
Анализ прочитанного(услышанного)
Сопоставление с известным
Оценка полученной
информации
Перекодировка ее в другие формы (таблицу, схему, рисунок и т.д.)
Слайд 5МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ. МАТЕРИАЛЬНАЯ
ТОЧКА.СИСТЕМА ОТСЧЕТА. ТРАЕКТОРИЯ.
ПУТЬ И ПЕРЕМЕЩЕНИЕ.
А1. Как
называют изменение положения тела относительно
другого?
Траекторией
Перемещением
Путем
Механическим
движением.
А2. Флажок по карте переместился из точки с координатами
х0 = - 4 см и у0 = - 3 см в точку с координатами х1 = 1 см и у1 = 1 см. Проекция вектора перемещения на ось У равна:
1. 5 см. 2. 4 см. 3. 3 см. 4. 2 см.
sy = y1 - y0
sy = 1 см – (- 3 см)= 4 см
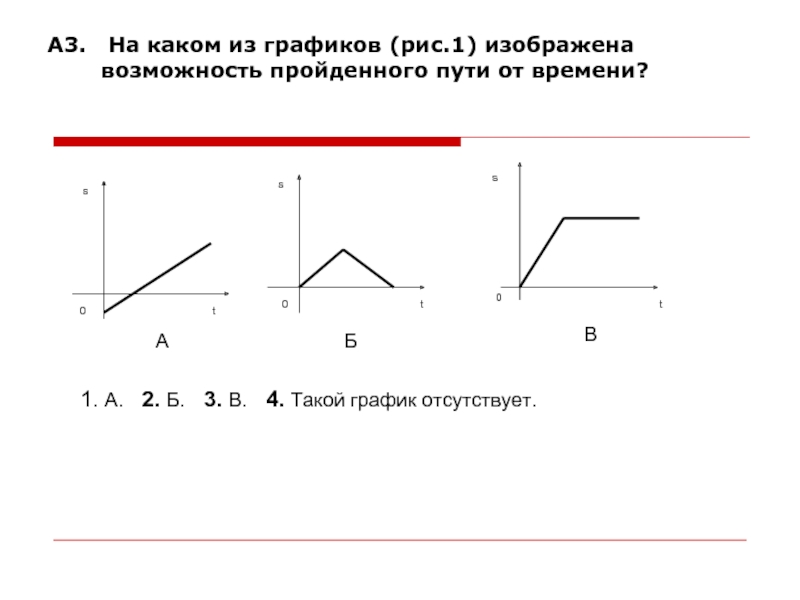
Слайд 7А3. На каком из графиков (рис.1) изображена возможность пройденного
пути от времени?
s
s
s
t
t
t
0
0
0
А
Б
В
1. А.
2. Б. 3. В. 4. Такой график отсутствует.
Слайд 8А3. решение
Формула расчета перемещение от времени:
Для равномерного движения s
= v · t (прямая, исходящая из нуля ; s
>0; s = 0)
Для равноускоренного движения s = v0t + аt2/2 ( парабола)
Т. О. Наиболее возможным будет ответ №3 – график В.
Слайд 9А4. Тело движется прямолинейно вдоль оси Х. На графике (рис.2)
представлена зависимость координаты тела от времени. В какой момент времени
модуль перемещения относительно исходной точки имел максимальное значение?
1 с.
2 с.
3 с.
6 с.
Слайд 10А4. Решение
По определению ПЕРЕМЕЩЕНИЕ – вектор, соединяющий начальное положение тела
с его конечным положением и направленный к конечному положению.
Формула расчета:
s = x – x0.
Анализ графика:
в момент t = 1 с s1 = х1 – х0 = |20 м – 10 м| = 10 м
в момент t = 2с s2 = х2 – х0 = |10 м – 10 м| = 0 м.
в момент t = 3с s3 = х3 – х0 = |0 м – 10 м| = 10 м
в момент t = 6 с s4 = х6 – х0 = |-10 м –10 м| = 20 м
Т.о. правильный ответ 4. 6с.
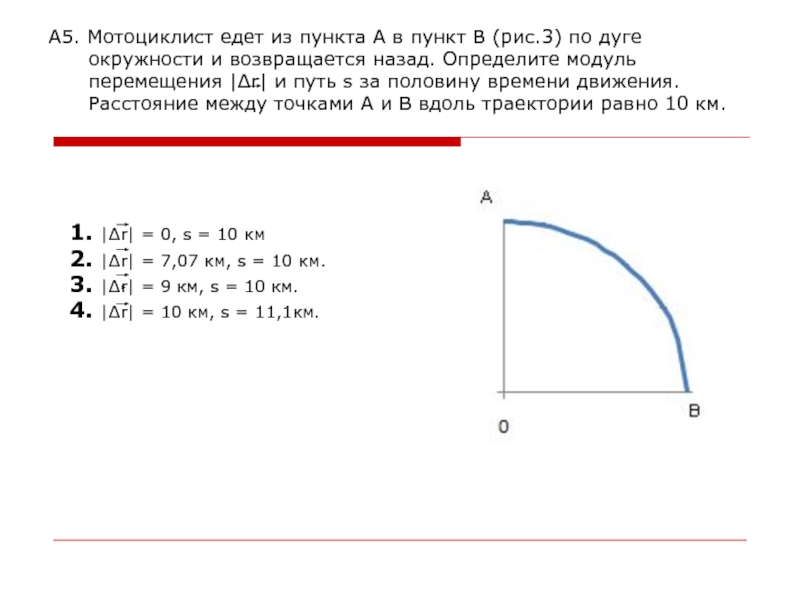
Слайд 11А5. Мотоциклист едет из пункта А в пункт В (рис.3)
по дуге
окружности и возвращается назад. Определите
модуль
перемещения |∆r| и путь s за половину времени движения.
Расстояние между точками А и В вдоль траектории равно 10 км.
1. |∆r| = 0, s = 10 км
2. |∆r| = 7,07 км, s = 10 км.
3. |∆r| = 9 км, s = 10 км.
4. |∆r| = 10 км, s = 11,1км.
В
Рис.3.
О
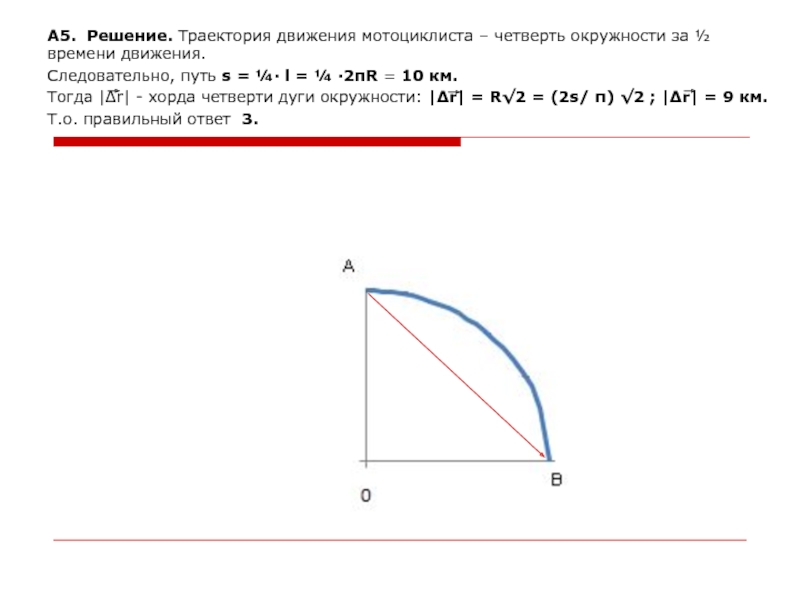
Слайд 12А5. Решение. Траектория движения мотоциклиста – четверть окружности за ½
времени движения.
Следовательно, путь s = ¼· l = ¼
·2πR = 10 км.
Тогда |∆r| - хорда четверти дуги окружности: |∆r| = R√2 = (2s/ π) √2 ; |∆r| = 9 км.
Т.о. правильный ответ 3.
Слайд 13II. Поступательное и вращательное движение. Скорость. Мгновенная и средняя скорость.
Ускорение.
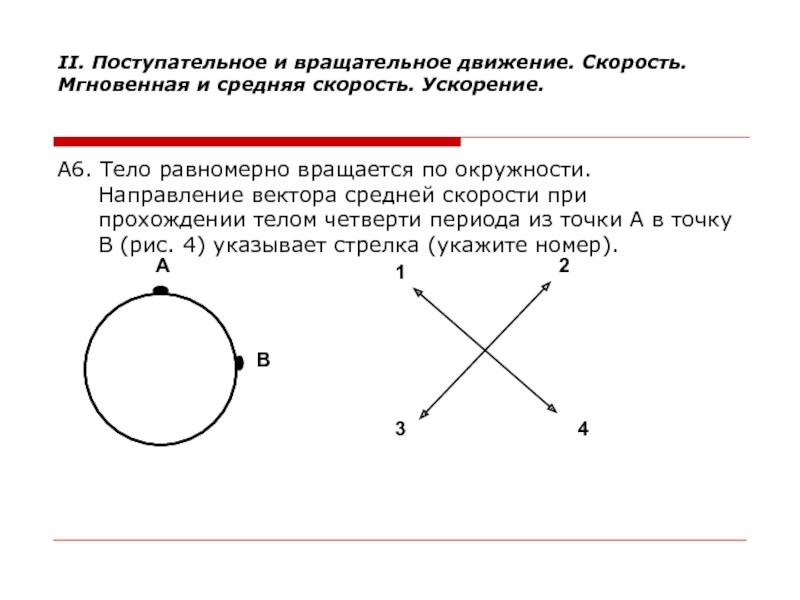
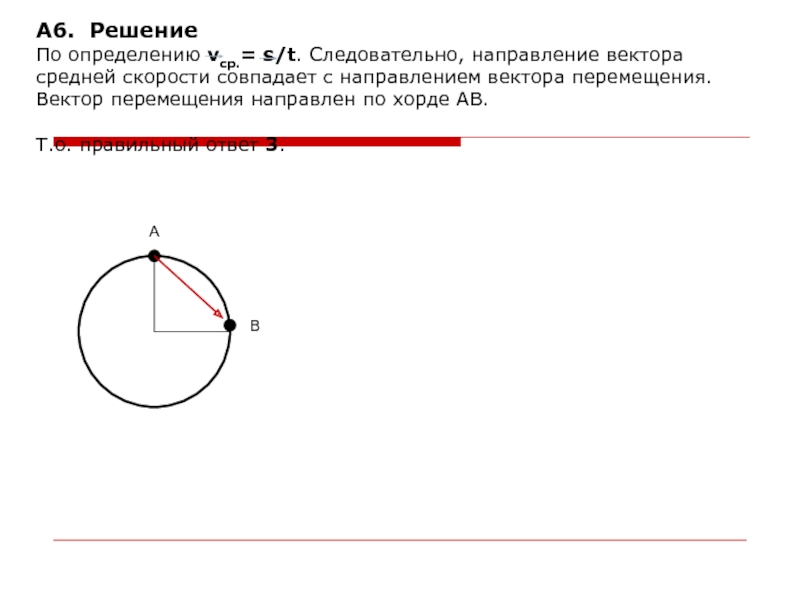
А6. Тело равномерно вращается по окружности. Направление вектора средней скорости
при прохождении телом четверти периода из точки А в точку В (рис. 4) указывает стрелка (укажите номер).
А
В
1
2
3
4
Слайд 14А6. Решение
По определению vср.= s/t. Следовательно, направление вектора средней скорости
совпадает с направлением вектора перемещения. Вектор перемещения направлен по хорде
АВ.
Т.о. правильный ответ 3.
А
В
Слайд 15А7. Поезд прошел первую половину пути со скоростью в n
раз большей, чем вторую. Какова скорость поезда на первой половине
пути?
vср.(1 + n)/2n
n vср./2
vср.(1 + n)/2
Среди ответов 1-3 нет правильного.
Решение:
vср.= (s1 + s2)/(t1 + t2) = s : (s1 / v1 + s2 / v2) = 2v1v2 / (v1 + v2)
vср. = 2·nv2· v2 / (v2n + v2)
vср. = 2·nv2 / (n + 1) = 2·v1 / (n + 1)
Т.о. v1 = vср.(1 + n)/2
Слайд 16III. Равномерное прямолинейное движение. Сложение скоростей. Относительность движения.
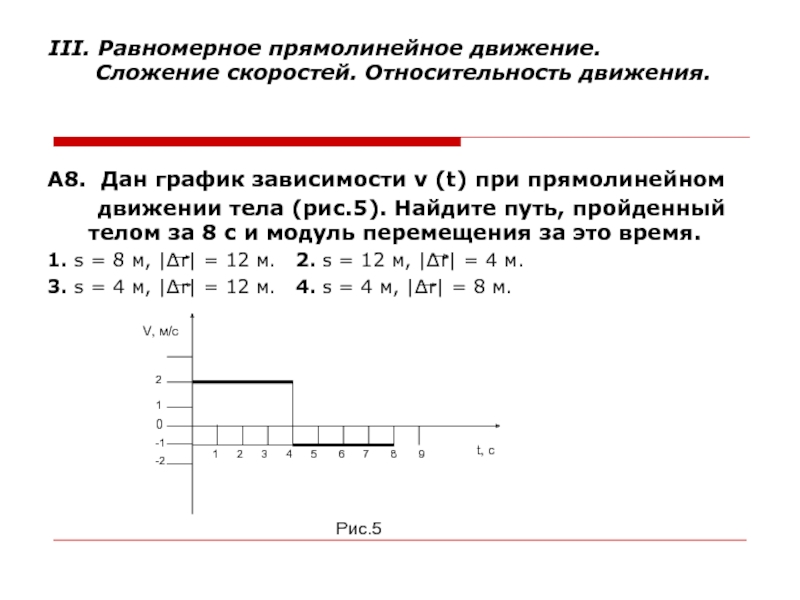
А8. Дан график
зависимости v (t) при прямолинейном
движении
тела (рис.5). Найдите путь, пройденный телом за 8 с и модуль перемещения за это время.
1. s = 8 м, |∆r| = 12 м. 2. s = 12 м, |∆r| = 4 м.
3. s = 4 м, |∆r| = 12 м. 4. s = 4 м, |∆r| = 8 м.
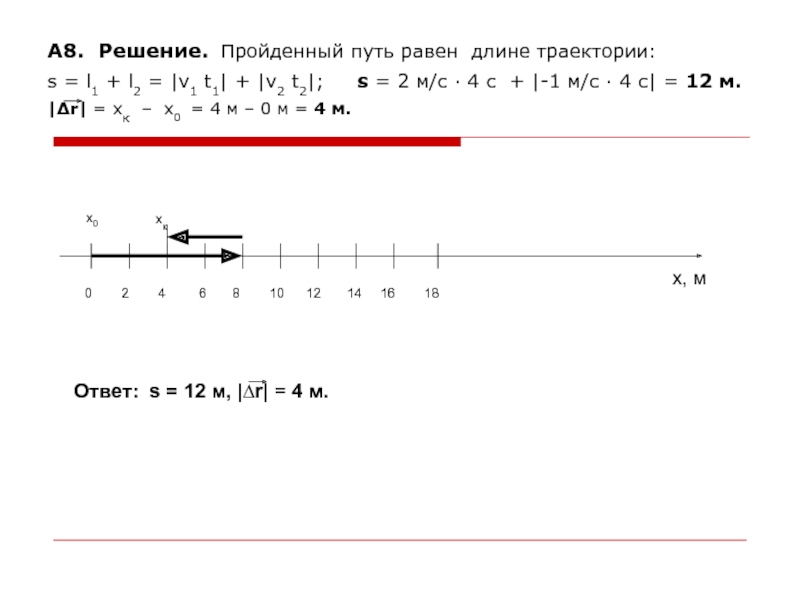
Слайд 17А8. Решение. Пройденный путь равен длине траектории:
s = l1
+ l2 = |v1 t1| + |v2 t2|;
s = 2 м/с · 4 с + |-1 м/с · 4 с| = 12 м.
|∆r| = хк – х0 = 4 м – 0 м = 4 м.
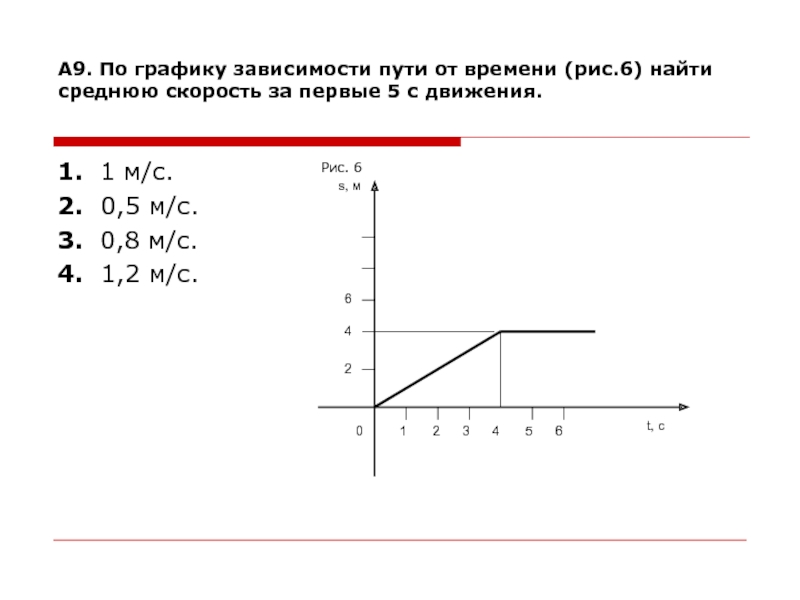
Слайд 18А9. По графику зависимости пути от времени (рис.6) найти среднюю
скорость за первые 5 с движения.
1. 1 м/с.
2. 0,5 м/с.
3.
0,8 м/с.
4. 1,2 м/с.
Рис. 6
Слайд 19А10. Пешеход идет по прямолинейному участку дороги со скоростью v.
Навстречу ему движется автобус со скоростью 10v. С какой
скоростью должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
1. 4,5 v. 2. 5,5 v. 3. 9 v. 4. 11 v.
Решение:
Vотн = v + nv
Vотн = 10v – nv,
т.о. v + nv = 10v – nv; v · (1+n) = v · (10 – n); 2n = 9;
n = 4,5.
Vвел = 4,5 v
Слайд 20IV. Равнопеременное прямолинейное движение. Графики зависимости кинематических величин от времени
при равномерном и равноускоренном движении.
А11. На рис. 7 представлен график
зависимости проекции скорости vx тела от времени t. Проекция ускорения и скорости имеют одинаковый знак на участках:
1. А и Г. 2. А и В. 3. Б и В. 4. В и Г.
На рисунке представлена фотография установки для исследования равноускоренного скольжения каретки
(1) массой 0,1 кг по наклонной плоскости, установленной под углом 30° к горизонту.
В момент начала движения верхний датчик (А) включает секундомер (2), а при прохождении каретки мимо нижнего датчика (В) секундомер выключается. Числа на линейке обозначают длину в сантиметрах. Какое выражение позволяет вычислить скорость каретки в любой момент времени?
1) υ = 1,25t
2) υ = 0,5t
3) υ = 2,5t
4) υ = 1,9t
Слайд 22
Решение:
В данном движении каретка движется без начальной
скорости v0 = 0.
Тогда s = at2 / 2. Отсюда
a = 2s / t2. a = 2·0,2 м / (0,4c)2 = 1,25 м/с2.
Таким образом, v = 1,25t.
Слайд 23
А13. Автомобиль движется по
прямой улице. На графике представлена зависимость скорости автомобиля от времени.
Модуль ускорения максимален в интервале времени
от 0 с до 10 с.
от 10 с до 20 с.
от 20 с до 30 с.
от 30 с до 40 с.
Слайд 24
Решение:
По графику видно, что скорость изменяется
за равные промежутки времени, следовательно, ускорение больше, если изменение скорости
больше: a = ∆v / t2.
Правильный ответ – 2) от 10с до 20 с.
Слайд 25V. Движение по окружности cпостоянной скоростью. Центростремительное ускорение, период и
частота обращения.
А14. Две материальные точки движутся по окружностям радиусами
R1 и R2, причем R2 = 2R1. При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением
1) a1 = 2a2 2) a1 = a2 3) a1 = a2 4) a1 = 4a2
Решение: aц = v2 / R
v2 = a1 R1 = a2 R2
a1 R1 = a2 2R1
a1 = 2a2
Слайд 26
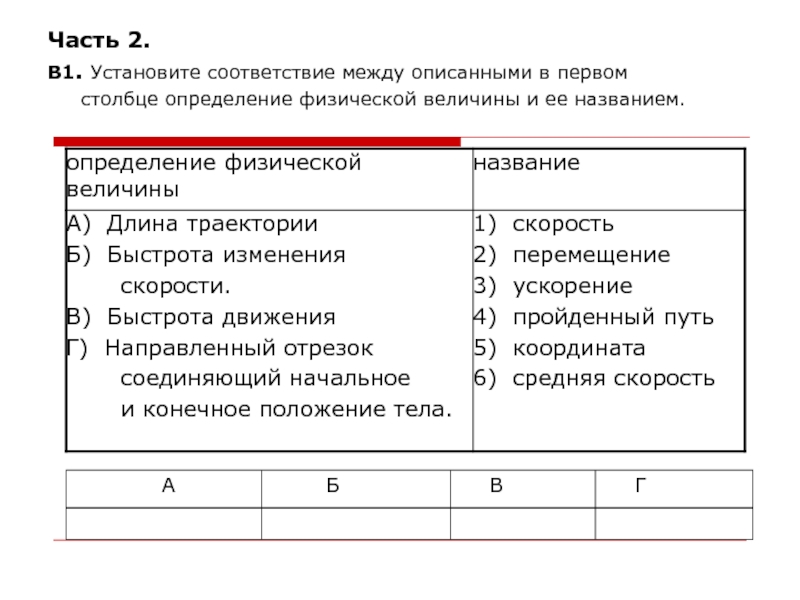
Часть 2.
В1. Установите соответствие между описанными в первом
столбце определение физической величины и ее названием.
А
Б
В
Г
Слайд 27VI. Ускорение свободного падения. Движение тела, брошенного вертикально и под
углом к горизонту.
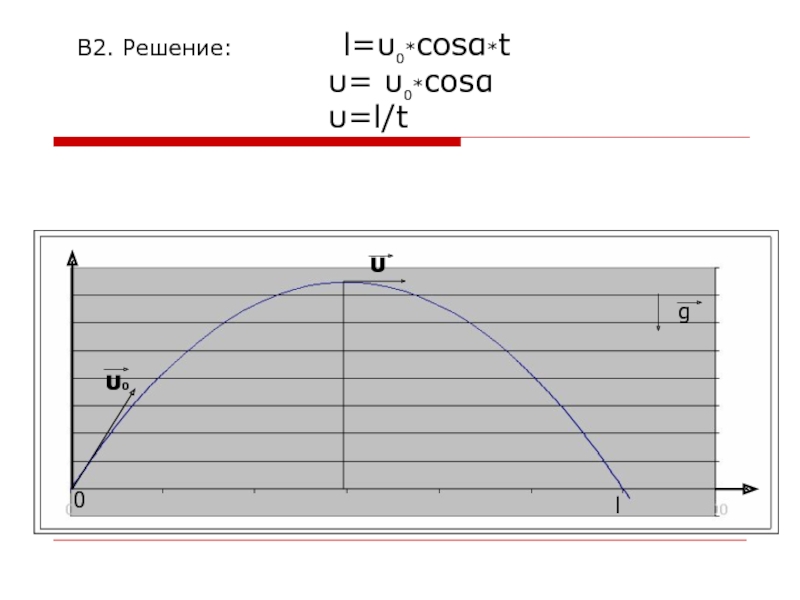
В2. Небольшой камень, брошенный с ровной горизонтальной
поверхности земли под углом к горизонту, упал обратно на землю в 20 м от места броска. Чему была равна скорость камня через 1 с после броска, если в этот момент она была направлена горизонтально?
В3. Тело брошено со стола горизонтально. При падении на пол его скорость равна 7,8 м/с. Высота стола Н = 1,5 м. Чему равна начальная скорость тела?
Слайд 28В2. Решение: l=υ0*cosα*t
υ= υ0*cosα