Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ
Содержание
- 1. КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ
- 2. Функция, во-первых, непрерывна, тогда как при корреляционной
- 3. 1. Кустистость растений (х): 4;
- 4. 2. Кустистость растений (х): 4; 6; 10;
- 5. Слайд 5
- 6. 3. Кустистость растений (х): 4; 6; 10;
- 7. Ранговый коэффициент корреляции Спирмена (rs) где
- 8. Коэффициент корреляции Пирсона Коэффициент корреляции Пирсона характеризует
- 9. Сильная или тесная
- 10. Слайд 10
- 11. Статистическая проверка наличия корреляции Гипотеза
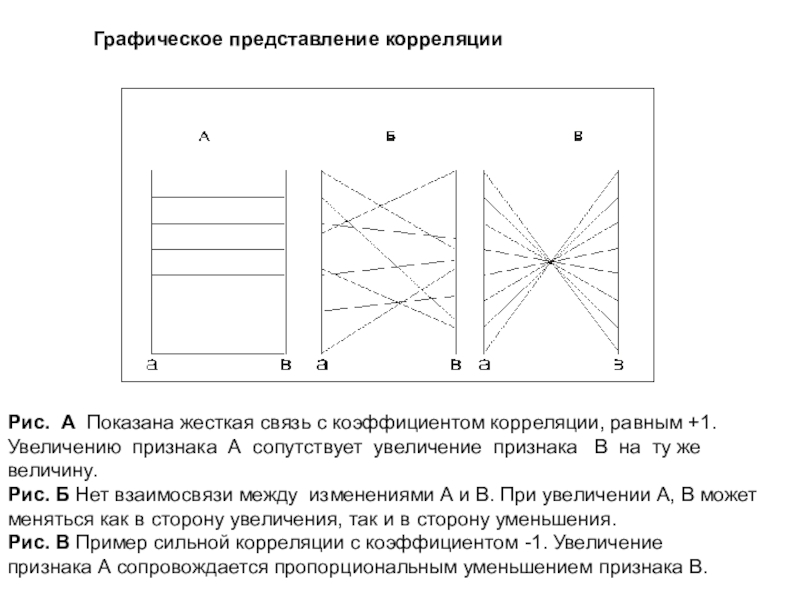
- 12. Графическое представление корреляцииРис. А Показана жесткая связь с
- 13. Линейная корреляция Предположим, что мы располагаем выборкой
- 14. Двумерная диаграмма рассеяния, отражающая линейную корреляцию между ростом и весом человека.
- 15. Вычисление же коэффициентов корреляции Пирсона предполагает, что
- 16. Слайд 16
- 17. Регрессия •Моделирование, описание зависимости между переменными•Количественная
- 18. Функция f(x2 , x3 , …, xт),
- 19. Уравнение регрессииY = b0+ b1X y =
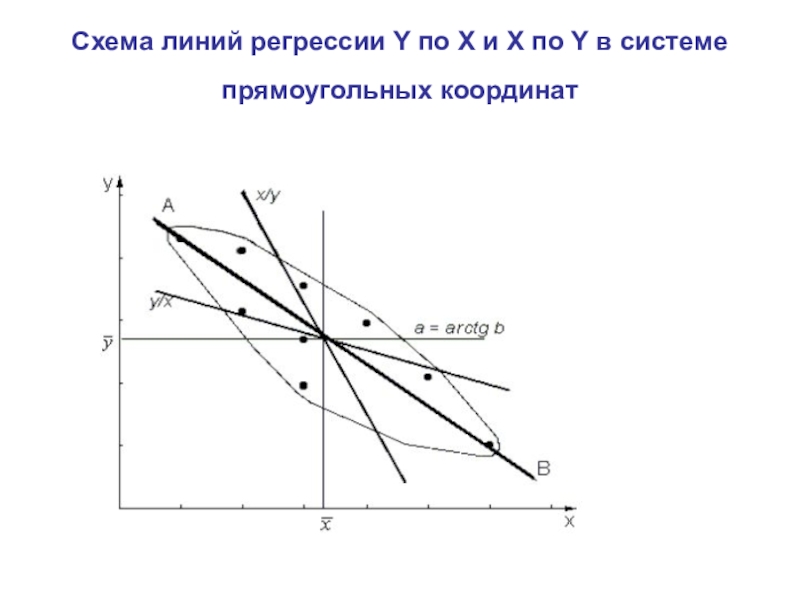
- 20. Схема линий регрессии Y по Х и Х по Y в системе прямоугольных координат
- 21. Коэффициенты уравнения парной линейной регрессииY = a1
- 22. Способ наименьших квадратовВ основу этого способа положена
- 23. Имеются данные измерений роста X (см) и
- 24. Корреляционное поле лучше всего описывается линейным уравнением
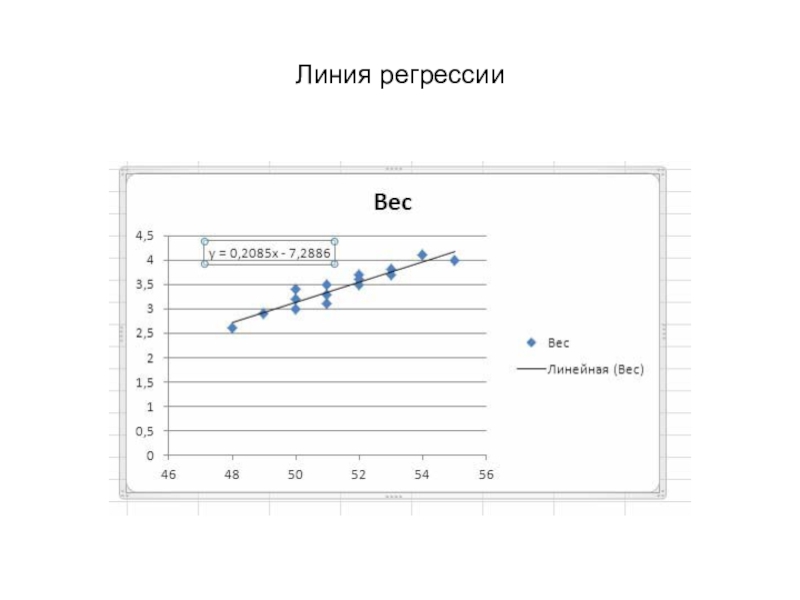
- 25. Линия регрессии
- 26. Расчет наилучшего соответствия веса для роста: 50,
- 27. Оценка веса ребенка ростом 55 см. Используем уравнение линейной регрессии.
- 28. Скачать презентанцию
Функция, во-первых, непрерывна, тогда как при корреляционной зависимости значения, принимаемые признаком, дискретны. Во-вторых, функциональная зависимость предполагает взаимно однозначное соответствие аргумента х и функции f(х), вероятностная же зависимость допускает некий условный диапазон, в который предположительно
Слайды и текст этой презентации
Слайд 2Функция, во-первых, непрерывна, тогда как при корреляционной зависимости значения, принимаемые
Слайд 3 1. Кустистость растений (х): 4; 6; 10; 12,
в среднем 8. Вес растений в г (у): 30;
34; 42; 46, в среднем 38.Слайд 42. Кустистость растений (х): 4; 6; 10; 12, в среднем
8.
Вес растений в г (у): 46; 42; 34; 30,
в среднем 38. Слайд 63. Кустистость растений (х): 4; 6; 10; 12, в среднем
8.
Вес растений в г (у): 42; 30; 46; 34,
в среднем 38 Слайд 7Ранговый коэффициент корреляции Спирмена (rs)
где х и у
— ранги по каждому признаку; п — число членов в
совокупности.Формула может быть упрощена, если выражение (х—у/)2 заменить на D2. Тогда
Слайд 8Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона характеризует существование линейной зависимости между
двумя величинами.
Пусть даны две выборки
коэффициент корреляции Пирсона рассчитывается
по формуле:Слайд 9Сильная или тесная
более 0,70
Средняя от 0,50 до 0,69
Умеренная от 0,30 до 0,49
Слабая от 0,20 до 0,29
Очень слабая меньше 0,19
Слайд 11
Статистическая проверка наличия корреляции
Гипотеза Но: : отсутствует линейная связь между
выборками х и у (
Статистика критерия:
– распределение Стьюдента с степенями свободы.)
Слайд 12Графическое представление корреляции
Рис. А Показана жесткая связь с коэффициентом корреляции, равным
+1. Увеличению признака А сопутствует увеличение признака В на ту же величину.
Рис. Б Нет взаимосвязи между изменениями А и
В. При увеличении А, В может меняться как в сторону увеличения, так и в сторону уменьшения. Рис. В Пример сильной корреляции с коэффициентом -1. Увеличение признака А сопровождается пропорциональным уменьшением признака В.
Слайд 13Линейная корреляция
Предположим, что мы располагаем выборкой данных о какой-то
группе объектов.
Пусть эти объекты обладают общими родовыми особенностями (примерно
одинаковы). Пусть, к тому же, у каждого из объектов можно количественно измерить, как минимум, два каких-либо параметра.
При этих обстоятельствах открывается возможность для подсчета линейной корреляции между двумя (или более) признаками, присущими этим объектам.
Например, такими выборками данных могут служить сведения о:
- группе людей, рост и вес тела которых мы измеряем;
- длине и ширине лепестка какого-нибудь цветка.
Слайд 14Двумерная диаграмма рассеяния, отражающая линейную корреляцию между ростом и весом
человека.
Слайд 15Вычисление же коэффициентов корреляции Пирсона предполагает,
что каждый из анализируемых
количественных признаков, подчиняется нормальному закону.
Гистограммы распределения для роста и
веса.Слайд 17Регрессия
•Моделирование, описание зависимости между переменными
•Количественная оценка поведения отклика при изменении
предиктора ->> уравнение регрессии
•Предсказание значений переменной отклика при заданных значениях
предиктора ->> прогнозСлайд 18Функция f(x2 , x3 , …, xт), описывающая зависимость показателя
от параметров, называется уравнением (функцией) регрессии.
Требуется: установить количественную взаимосвязь
между показателем и факторами. В таком случае задача регрессионного анализа понимается как задача выявления такой функциональной зависимости y* = f(x2 , x3 , …, xт), которая наилучшим образом описывает имеющиеся экспериментальные данные.Регрессия — зависимость математического ожидания (например, среднего значения) случайной величины от одной или нескольких других случайных величин (свободных переменных), то есть
Регрессионным анализом называется поиск такой функции , которая описывает эту зависимость. Регрессия может быть представлена в виде суммы неслучайной и случайной составляющих.
где — функция регрессионной зависимости, а — аддитивная случайная величина с нулевым матожиданием.
Слайд 19Уравнение регрессии
Y = b0+ b1X
y = a + bx
Y –зависимая переменная, отклик
X –независимая переменная, предиктор, фактор
b0 ,а–ожидаемое
значение Y при X= 0свободный член; графически он представляет отрезок ординаты (у) в системе прямоугольных координат.
b1– коэффициент регрессии
угол наклона графика по отношению к оси X, среднее изменение Y на единицу изменения Х в выборке
Слайд 21Коэффициенты уравнения парной линейной регрессии
Y = a1 + by/xX —
прямое
и X = a2 + bx/yY — обратное, (2.2)
где: a
и b – коэффициенты, или параметры, которые надлежит определить.Значение коэффициентов регрессии вычисляется по формуле:
Коэффициенты а определяются по формуле
Слайд 22Способ наименьших квадратов
В основу этого способа положена теорема, согласно которой
сумма квадратов отклонений вариант (xi) от средней арифметической () есть
величина наименьшая, т. е.Графическое изображение эмпирического уравнения регрессии.
то функция называется регрессией величины Y по величинам
Слайд 23Имеются данные измерений роста X (см) и веса Y (кг)
новорождённых:
Проведите регрессионный анализ: составьте уравнение линейной регрессии и таблицу наилучшего
соответствия веса для роста: 50, 51 и 52 см. Оцените вес ребенка ростом 55 см.