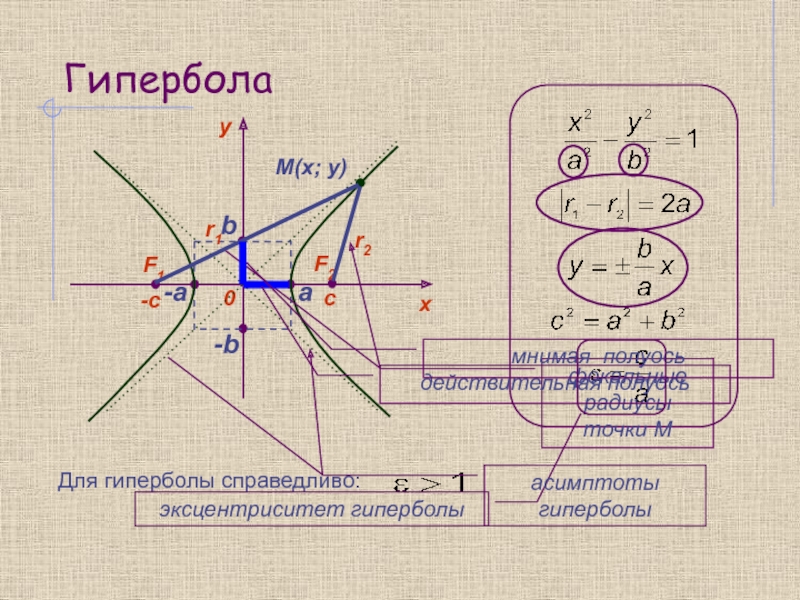
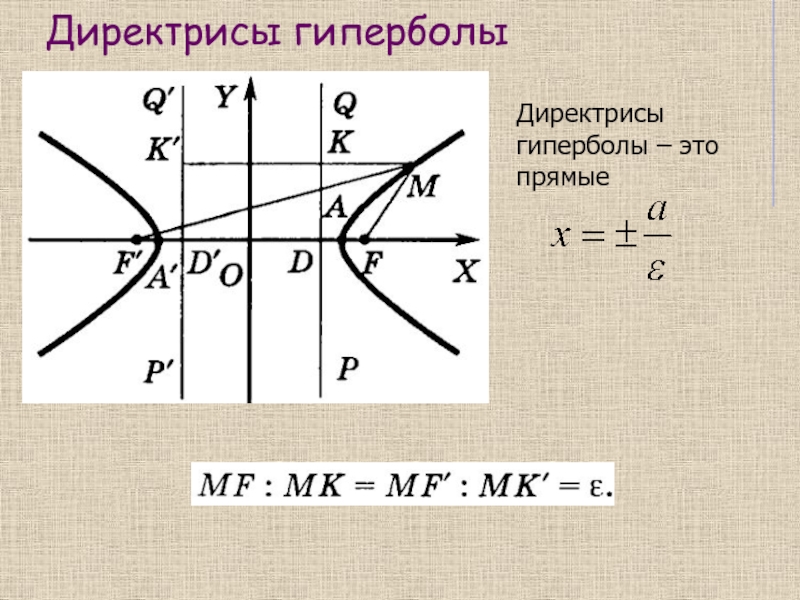
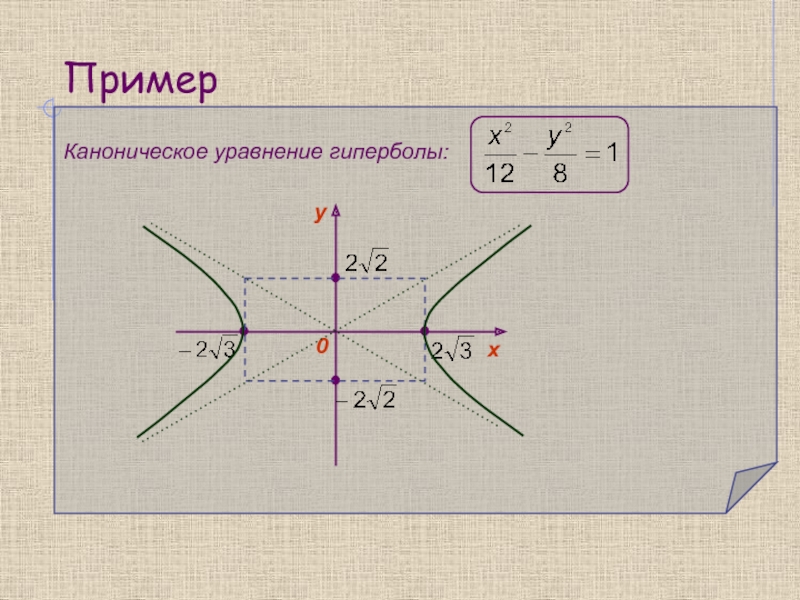
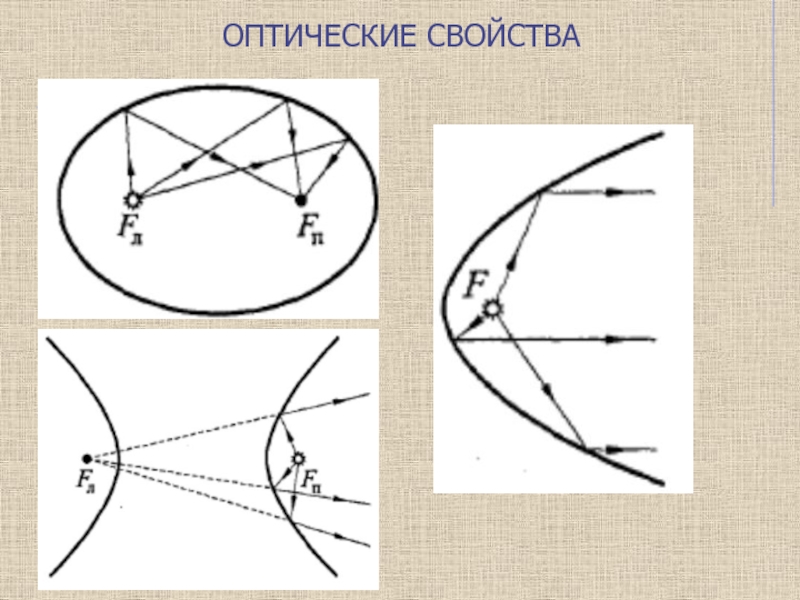
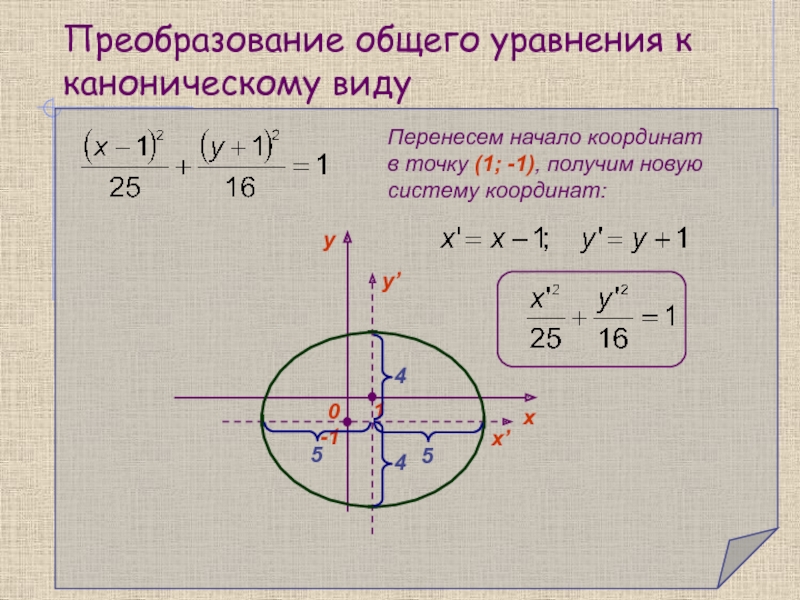
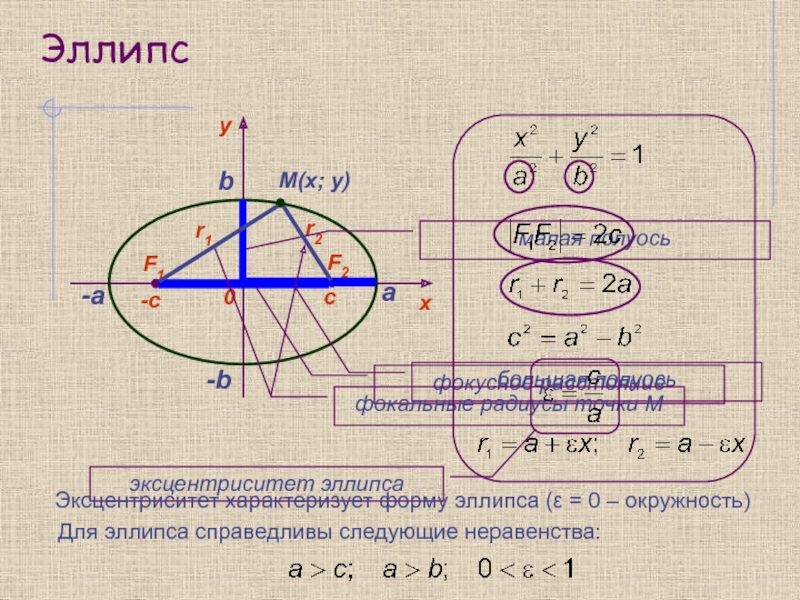
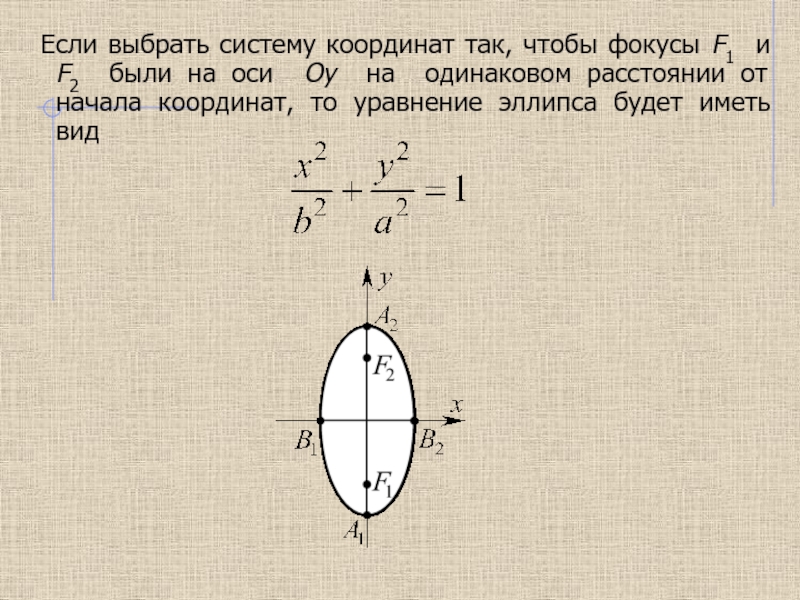
эллипс, частным случаем которого является окружность, гипербола и парабола.
Общее уравнение
кривой второго порядкаВ некоторых частных случаях это уравнение может определять также две прямые, точку или мнимое геометрическое место.


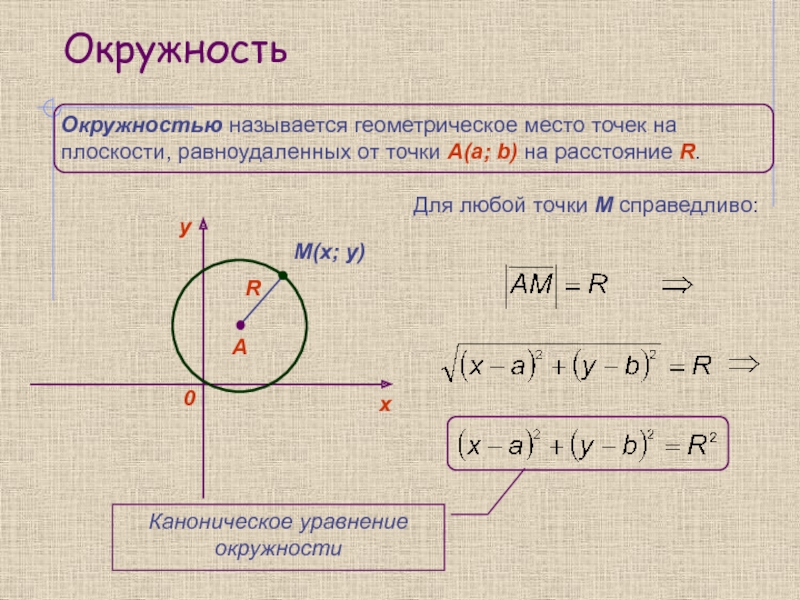

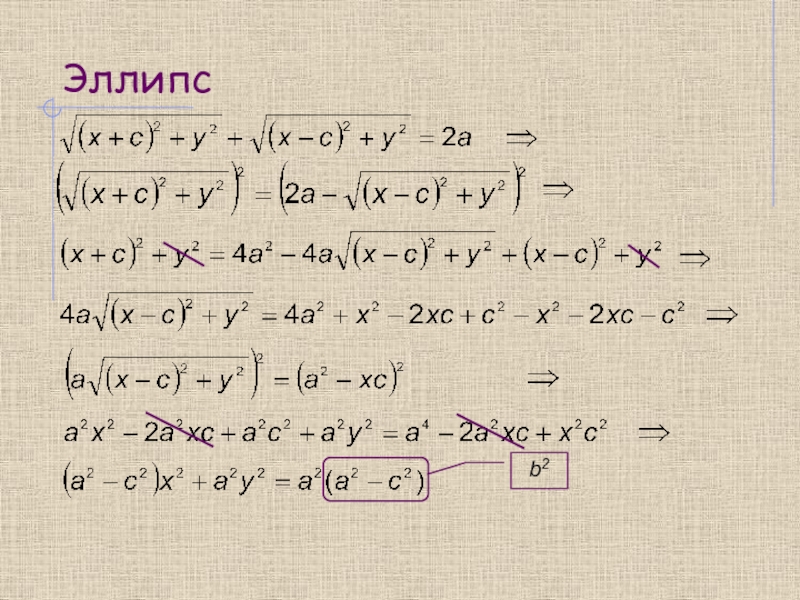

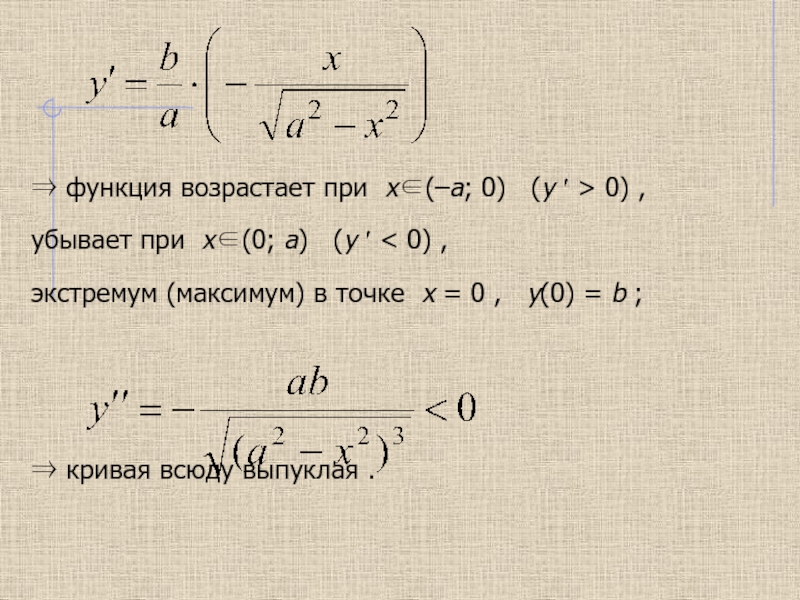





![Кривые второго порядка а) D(y) = (– ;–a] ∪ [a; +) , y(a) = 0 ; б) линия имеет а) D(y) = (– ;–a] ∪ [a; +) , y(a) = 0 ; б) линия](/img/thumbs/61683856792308f41b2e4656ca96cc17-800x.jpg)