Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 4 Многомерность (проклятье размерностей, т.Эйлера на поверхностях рода
Содержание
- 1. Лекция 4 Многомерность (проклятье размерностей, т.Эйлера на поверхностях рода
- 2. Преодоление «проклятья размерности» и его цена Теорема.
- 3. Теорема Турана о существовании у графа G
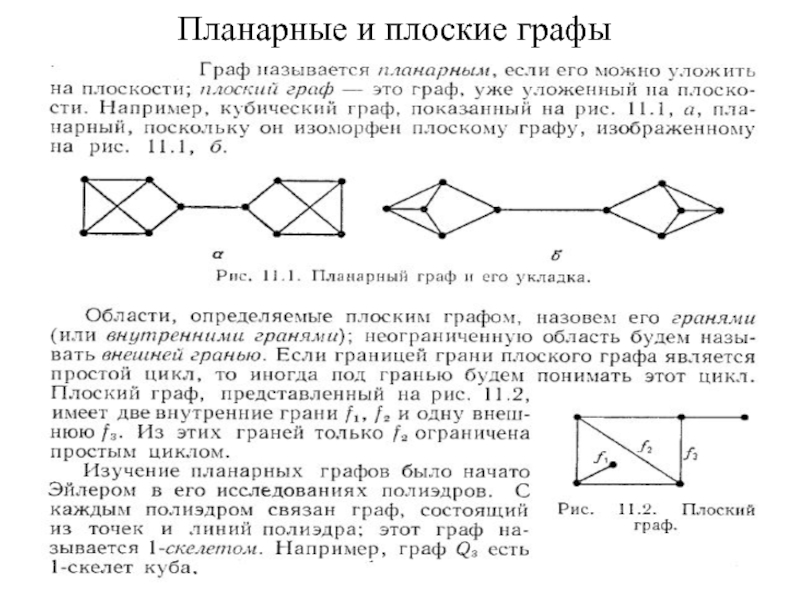
- 4. Планарные и плоские графы
- 5. Теорема Эйлера (для плоскости – сферы и
- 6. Теорема Эйлера (продолжение)Возьмём остов (дерево) любого плоского
- 7. Теорема о плоской картеЕсли графу G соответствует
- 8. Теорема Куратовского - ПонтрягинаД-во. 1) Проверим планарность
- 9. Фрагмент из книги Ф.Харари «Теория графов», М.: МИР, 1973
- 10. Модель К.Левина жизненного пространства личности L –
- 11. Теорема Куратовского - ПонтрягинаD = 4D=5К5К3,3
- 12. Построение многомерной сети Рассмотрим граф n –
- 13. Сферическая поверхность - род «γ=0» и граф
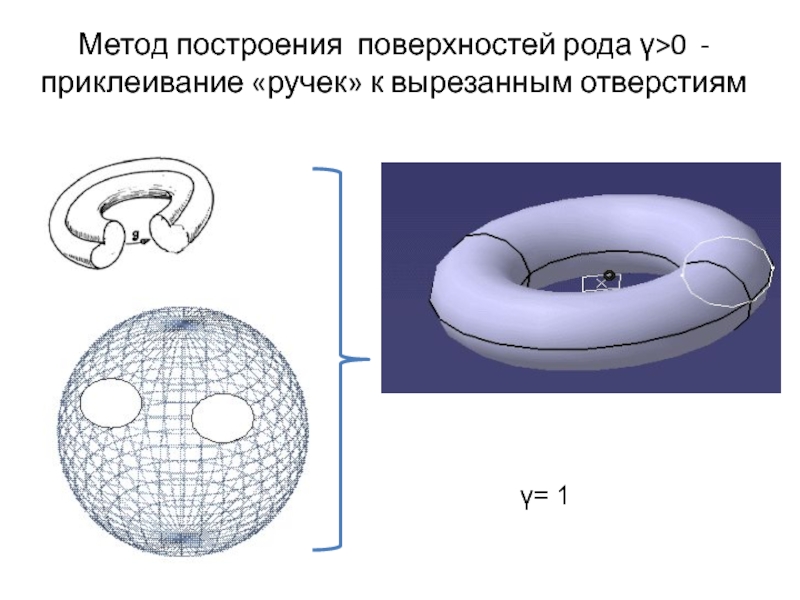
- 14. Метод построения поверхностей рода γ>0 - приклеивание «ручек» к вырезанным отверстиямγ= 1
- 15. Минимальная сеть - граф 4-х куба для
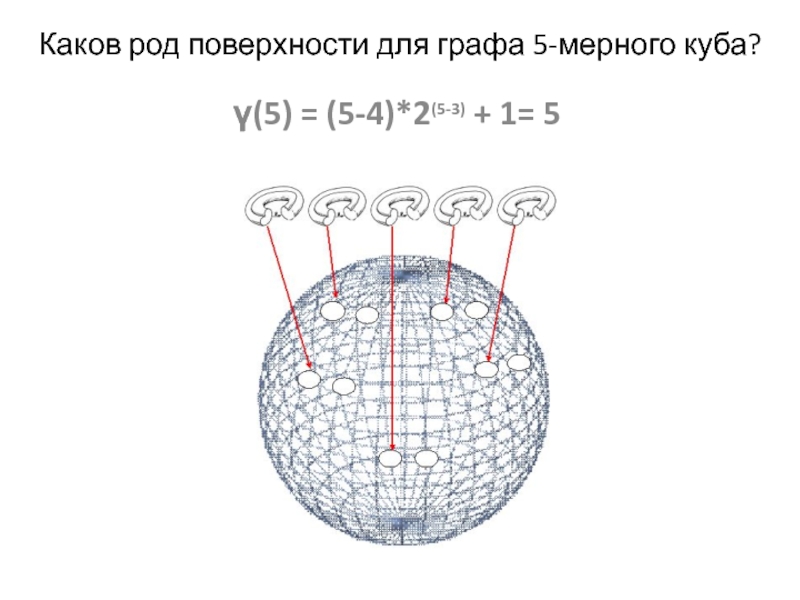
- 16. Каков род поверхности для графа 5-мерного куба?γ(5) = (5-4)*2(5-3) + 1= 5
- 17. Вид минимальной «безсветофорной» сети для пространства личности
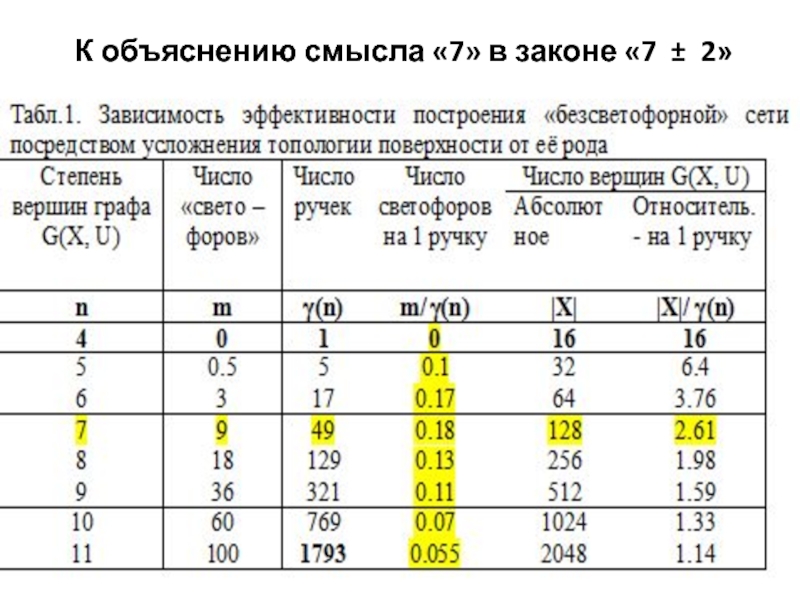
- 18. Оценки min числа неустранимых рёберных пересечений для
- 19. К объяснению смысла «7» в законе «7 ± 2»
- 20. Характеристика Эйлера-Пуанкаре χ графа многомерной сети
- 21. Связь с гауссовой кривизнойхарактеристика Эйлера-Пуанкаре связана со
- 22. ∫Кds -интеграл по поверхности сопряжения ручки со
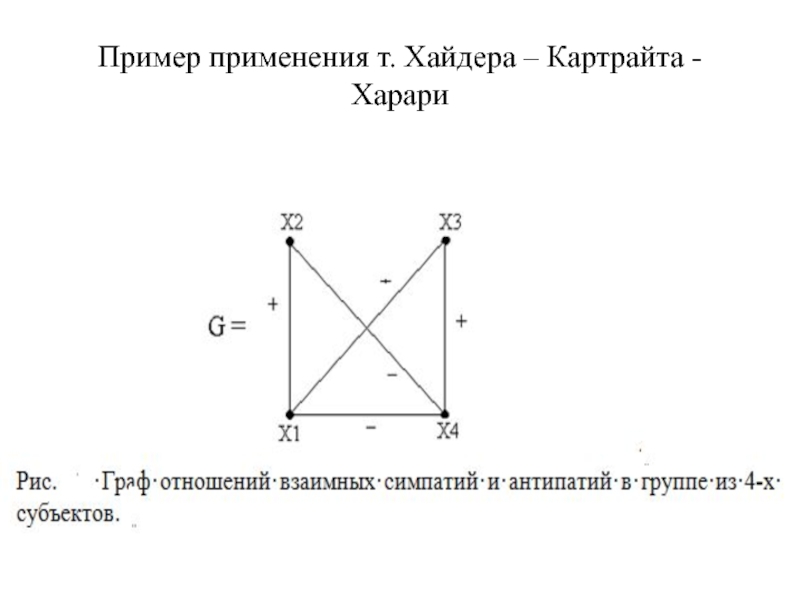
- 23. Знаковые графы и структурная теорема
- 24. Пример применения т. Хайдера – Картрайта - Харари
- 25. Литература1. Емеличев В.А. Мельников О.И. и др.
- 26. Скачать презентанцию
Преодоление «проклятья размерности» и его цена Теорема. Для любого конечного графа Gр ={V, E}, | V |
Слайды и текст этой презентации
Слайд 1Лекция 4 Многомерность («проклятье размерностей», т.Эйлера на поверхностях рода ≥0, знаковые
графы и др.)
социологии»Слайд 2Преодоление «проклятья размерности» и его цена
Теорема. Для любого конечного
графа Gр ={V, E}, | V |
реализация в трёхмерном пространстве R3 .Док-во. Возьмём в R3 –пространстве прямую и расположим на ней все вершины V1, V2, …, Vp. Пусть число рёбер |E|= q. Проведём через прямую связку плоскостей в количестве q. Получится «книга с q страницами», на каждой из которых разместится по одному ребру, концы которых будут упираться в свою пару вершин ViVj. ЧТД.
Слайд 3Теорема Турана о существовании у графа G треугольника
Док. во. Отношение
[] означает ближайшее целое число, меньшее вычисленного в
скобках. Для
малых р, например, 3 или 4, утверждение очевидно: для р=3 [р2 /4] = 2, для р= 4 [р2 /4] = 3. Будем доказывать методом индукции (для чётных р, - для
нечётных доказываете сами). Итак, пусть утверждение справедливо для всех чётных
Р ≤ 2n. Докажем его для р = 2n + 2.
Тогда возьмём граф G с 2n + 2 – вершинами и не содержащий треугольников. Из факта связности графа вытекает существование у него пары смежных вершин u, v.
В подграфе G1 = G – {u,v} имеется 2n вершин и нет треугольников, так что по
предположению индукции в графе G1 самое большее [4n2 /4] = n2 рёбер. Подсчитаем,
сколько рёбер может быть в графе G.
В графе G не существует такой вершины w, смежной с u, v, ибо тогда в нём был бы треугольник. Таким образом, если вершина u смежна с k вершинами, то вершина v может быть смежна самое большее с 2n – k вершинами. Поэтому в графе G не более, чем
n2 + k + (2 n - k) + 1 = (n + 1) = [ p2 /4]
рёбер. «ЧТД»
Слайд 5Теорема Эйлера (для плоскости – сферы и 2-мерной поверхности рода
γ≥1)
Формула Эйлера: V-E+F = 2 – 2γ, для сферы γ
=0Слайд 6Теорема Эйлера (продолжение)
Возьмём остов (дерево) любого плоского n-графа, в котором
имеются циклы. В таком графе число вершин р=n, а число
рёбер q=n-1 и число граней r =1, ибо циклов нет, а есть только одна внешняя грань, т.е.р - q+r = 2
Будем достраивать по 1 ребру остов до его первоначального графа, и тогда каждое новое ребро доставляет ещё и одну новую грань, что оставляет справедливой приведённую формулу, ч.т.д.
Слайд 7Теорема о плоской карте
Если графу G соответствует плоская (p,q)- карта,
в которой каждая грань является n – циклом, т.е. содержит
n – рёбер, тоq= n*(p-2)/(n-2) (&)
Д-во: Поскольку каждая грань графа G есть n – цикл, то любое ребро принадлежит двум граням, а каждая грань содержит n – рёбер. Отсюда: n*r = 2q.
Подставим это выражение в р - q+r = 2:
р- q + 2q/n = 2 p-2 = q*(1-2/n) Отсюда (&) Ч.т.д.
Для максимальных планарных графов:
Следствие 1: Если длина цикла n =3, то q = 3 p – 6;
Следствие 1: Если длина цикла n =4, то q = 2 p – 4;
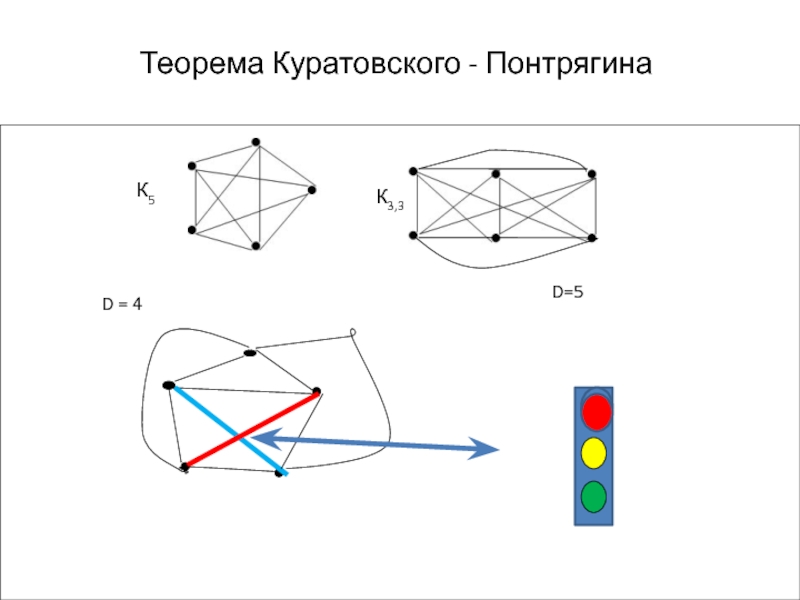
Слайд 8Теорема Куратовского - Понтрягина
Д-во. 1) Проверим планарность графа К5 :
p=5, q –число рёбер
Условие планарности: q≤ 3p-6, т.е. qплан =
9, но в К5 q = 10,Аналогично для К3,3 : qплан = 12, а по факту для К3,3 q = 16
2)Так как графы К5 и К3,3 непланарны, то это значит, что содержащие их в качестве подграфов графы также непланарны, ч.т.д.
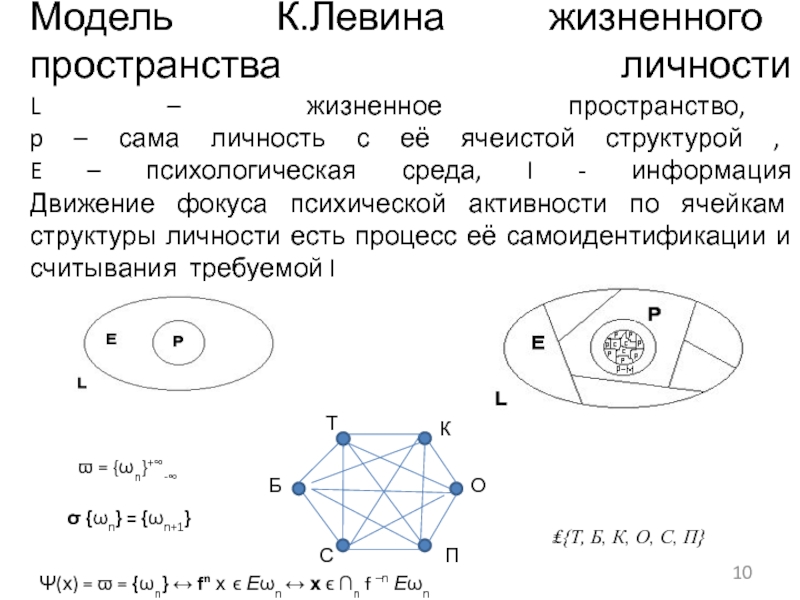
Слайд 10Модель К.Левина жизненного пространства личности L – жизненное пространство, p –
сама личность с её ячеистой структурой , E – психологическая
среда, I - информация Движение фокуса психической активности по ячейкам структуры личности есть процесс её самоидентификации и считывания требуемой IТ
Б
К
О
С
П
σ {ωn} = {ωn+1}
ϖ = {ωn}+∞-∞
Ψ(х) = ϖ = {ωn} ↔ fn х ϵ Еωn ↔ х ϵ ∩n f –n Еωn
₤{Т, Б, К, О, С, П}
Слайд 12Построение многомерной сети
Рассмотрим граф n – мерного куба, т.е.
удалим все грани и оставим только вершины и рёбра (такой
граф не является полным). Тогда минимальный род двумерных поверхностей, на которых такой граф будет представлен без пересечений ребер, записывается формулой:γ(n) = (n-4)*2(n-3) + 1
Байнеке Л.В., Харари Ф. (1974)
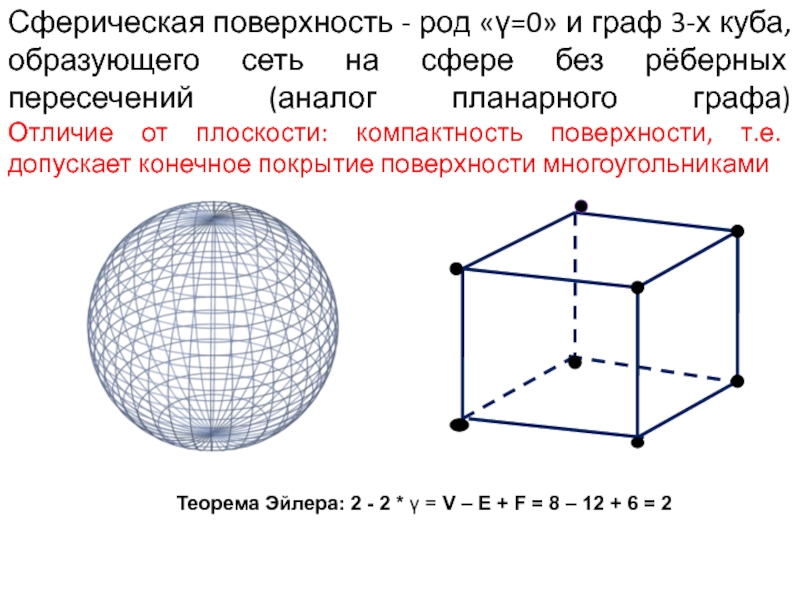
Слайд 13Сферическая поверхность - род «γ=0» и граф 3-х куба, образующего
сеть на сфере без рёберных пересечений (аналог планарного графа) Отличие от
плоскости: компактность поверхности, т.е. допускает конечное покрытие поверхности многоугольникамиТеорема Эйлера: 2 - 2 * γ = V – E + F = 8 – 12 + 6 = 2
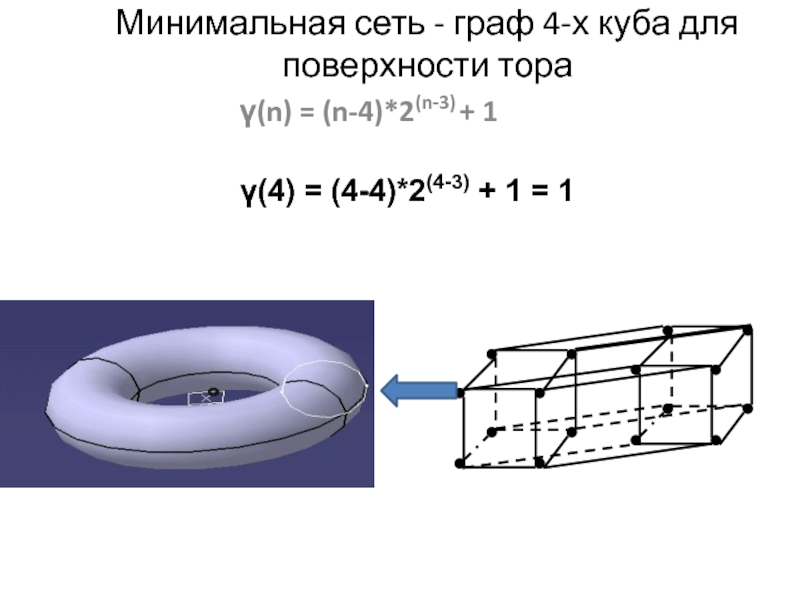
Слайд 15Минимальная сеть - граф 4-х куба для
поверхности тора
γ(n) = (n-4)*2(n-3)
+ 1
γ(4) = (4-4)*2(4-3) + 1 = 1
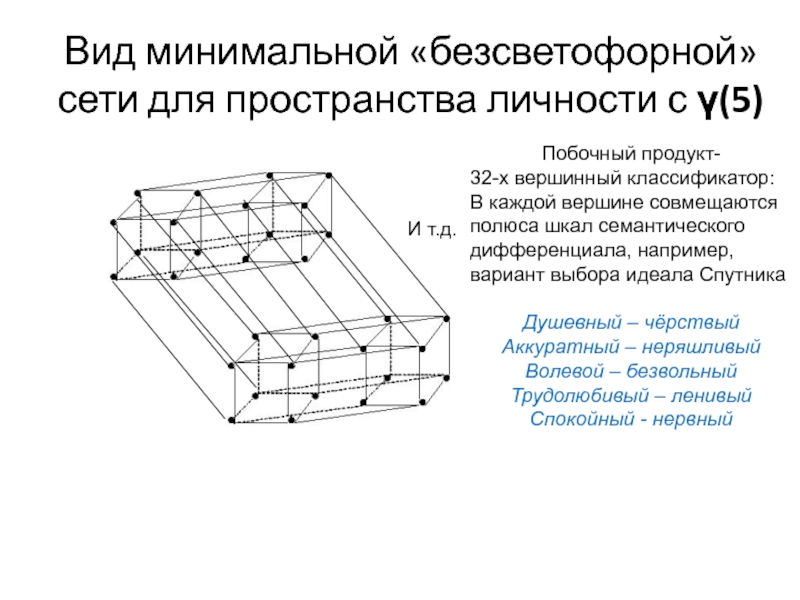
Слайд 17Вид минимальной «безсветофорной» сети для пространства личности с γ(5)
И
т.д.
Побочный продукт-
32-х вершинный классификатор:
В каждой вершине совмещаются
полюса шкал семантического
дифференциала,
например, вариант выбора идеала Спутника
Душевный – чёрствый
Аккуратный – неряшливый
Волевой – безвольный
Трудолюбивый – ленивый
Спокойный - нервный
Слайд 18 Оценки min числа неустранимых рёберных пересечений для обыкновенных графов, расположенных
на плоскости
это наименьшее число, согласно Т.Саати (1964), не превосходит
1/64
* n* (n-2)2 * (n-4) - при n чётном и не превосходит
1/64 * (n-1)2 * (n-3)2 - при n нечётном
Слайд 20Характеристика Эйлера-Пуанкаре χ графа
многомерной сети на поверхности рода р
Эта
характеристика в данном контексте – «р = γ(n)» - определяется
какχ = 2 – 2р = 2 – (n-4)*2(n-2) – 2 = (4-n)*2(n-2)
Слайд 21Связь с гауссовой кривизной
характеристика Эйлера-Пуанкаре связана со средним по поверхности
от величины гауссовой кривизны:
∫КdS = 2π χ
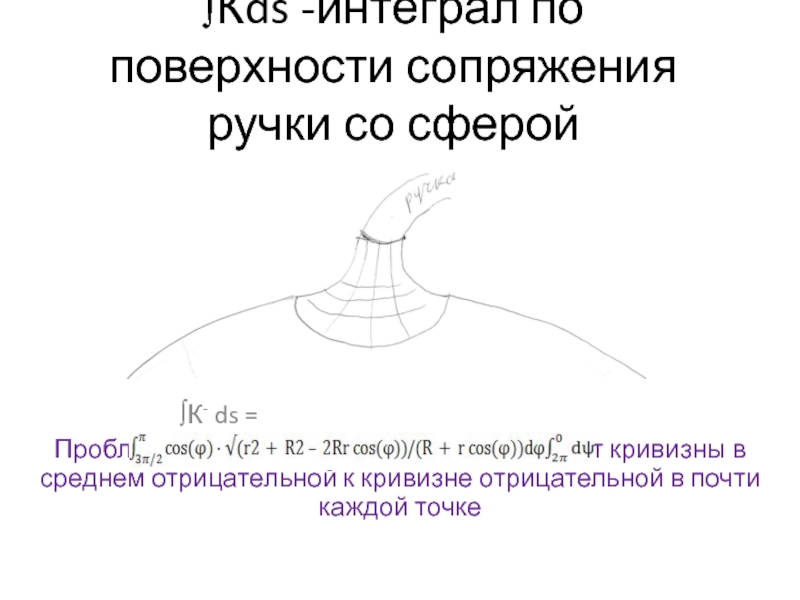
Слайд 22∫Кds -интеграл по поверхности сопряжения ручки со сферой
∫К- ds
=
Проблема подбора метрики для перехода от кривизны в среднем отрицательной
к кривизне отрицательной в почти каждой точке
Слайд 25Литература
1. Емеличев В.А. Мельников О.И. и др. Лекции по теории
графов: Учебное пособие. Изд. 4-е. М.: ЛЕНАНД, 2015.- 390 с.
2.
Оре О. Теория графов. – М.: Книжный дом «ЛИБРОКОМ»/URSS, 2009. – 352 c.3. Харари Ф. Теория графов. – М.:КомКнига /URSS, 2006. – 296 c.
4. Панюкова Т.А. Комбинаторика и теория графов: Учебное пособие. Изд. 3-е. испр. М.: ЛЕНАНД, 2014.- 216 с.


![Лекция 4 Многомерность (проклятье размерностей, т.Эйлера на поверхностях рода Теорема Турана о существовании у графа G треугольникаДок. во. Отношение [] Теорема Турана о существовании у графа G треугольникаДок. во. Отношение [] означает ближайшее целое число, меньшее вычисленного](/img/thumbs/e6ec8d2d6ee9dc7563423ef0b1e516c2-800x.jpg)