Лекция 9. Интерференция поляризованных волн. Искусственная анизотропия

9.2. Искусственная анизотропия, возникающая при деформациях. Явление Керра. Явление Коттон

- Мутона
9.3. Вращение плоскости поляризации в оптически активных средах
9.4. Явление Фарадея
9.5. Эффект Зеемана. Элементарная теория нормального эффекта Зеемана
9.6. Обратный эффект Зеемана и его связь с явлением Фарадея
9.7. Эффект Штарка

поляризованны во взаимно ортогональных направлениях. Для того, чтобы наблюдать интерференцию

необходимо свести два взаимно ортогональных когерентных колебания к одной плоскости. Этого можно добиться, поставив на пути светового пучка, поляризатор. В этом случае интерференция будет обеспечена и результат её окажется в зависимости от оптической разности хода складываемых волн.
Рассмотрим пластинку, вырезанную из одноосного кристалла, оптическая
ось которой параллельна ее поверхности. В этом случае при нормальном
падении света оба преломленных луча - обыкновенный и необыкновенный – распространяются в одном направлении - нормально к плоскости пластинки, но с различными фазовыми скоростями. По выходу из пластинки между лучами образуется разность хода, равная Δl = d(no – ne), где no – показатель преломления обыкновенного луча, ne – показатель преломления необыкновенного луча, d - толщина пластинки. Лучи когерентны, и должна возникнуть интерференция.

в одной плоскости Р2Р2 и имеют постоянный во времени сдвиг

фаз ΔΦ можно использовать графический метод сложения гармонических колебаний. Для этого в абстрактной плоскости будем изображать колебания «стрелочками», т.е. векторами. При этом модуль вектора задаёт амплитуду колебания, а угол наклона вектора по отношению к горизонтальной линии определяет фазу колебания. Замечательно, то, что в такой абстрактной картинке суммарное колебание получаем как векторную сумму двух рассматриваемых колебаний, т.е. по правилу треугольника.

– Мутона Анизотропия при деформациях
Обычные прозрачные тела, не обладающие двойным

лучепреломлением, при деформации сжатия или растяжения приобретают свойства одноосного кристалла, оптическая ось которого направлена вдоль деформирующих сил. Экспериментально установили следующую связь между показателями преломления необыкновенной и обыкновенной волн в направлении ортогональном так называемой оптической оси, т.е. направления внешних сил деформации: ne – no = kσ, где σ – напряжение (Па = Н/м2), коэффициент, зависящий от свойств вещества. Разность (ne – no) может принимать как положительные,
так и отрицательные значения. Вообще
говоря, возможна дисперсия показателей
ne и no , т.е. зависимость их от длины
волны λ.

плоскости пропускания которых составляют угол с направлением деформации. Деформируемое тело

в зависимости от распределенных в нём напряжений приобретает в проходящем свете систему так или иначе расположенных полос с максимумами и минимумами освещенности разных цветов.
При изменении напряжения картина меняется. Таким образом, наблюдая распределение цветовой освещенности по объему тела, можно судить о распределении напряжений на разных участках. Это свойство используют при исследовании распределения напряжений в сложных трудно рассчитываемых конструкциях – изготавливают геометрически подобную модель из прозрачного материала. Подвергают различным нагрузкам и по наблюдаемой в рассмотренной установке картине судят о распределении внутренних напряжений.

электрическом поле приобретает оптические свойства одноосного кристалла с оптической осью

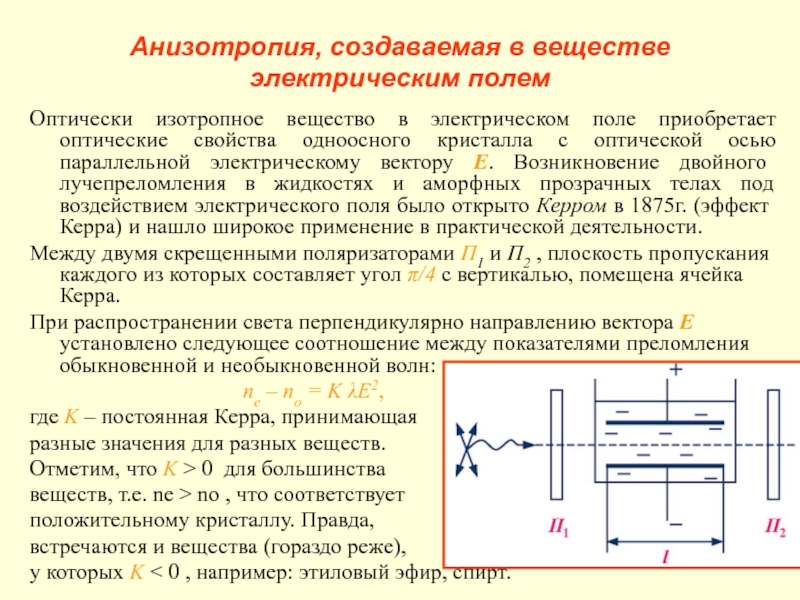
параллельной электрическому вектору Е. Возникновение двойного лучепреломления в жидкостях и аморфных прозрачных телах под воздействием электрического поля было открыто Керром в 1875г. (эффект Керра) и нашло широкое применение в практической деятельности.
Между двумя скрещенными поляризаторами П1 и П2 , плоскость пропускания каждого из которых составляет угол π/4 с вертикалью, помещена ячейка Керра.
При распространении света перпендикулярно направлению вектора E установлено следующее соотношение между показателями преломления обыкновенной и необыкновенной волн:
ne – no = K λE2,
где K – постоянная Керра, принимающая
разные значения для разных веществ.
Отметим, что K > 0 для большинства
веществ, т.е. ne > no , что соответствует
положительному кристаллу. Правда,
встречаются и вещества (гораздо реже),
у которых K < 0 , например: этиловый эфир, спирт.

газов постоянная по естественным причинам значительно меньше, например, у кислорода

при нормальных условиях K = 0,45 ∙10-15 м/В2. Связано это с тем, что эффект Керра – молекулярный эффект (определяется непосредственно свойствами молекул) и усиливается с повышением концентрации молекул. Рекордсменом здесь является нитробензол – K = 2.2 ∙10-10 см/В2. Постоянная Керра зависит также от длины волны света (дисперсия) и уменьшается с повышением температуры.
На пути ℓ в конденсаторе между обыкновенной и необыкновенной волнами возникает разность фаз:



При изменении напряженности электрического поля Е меняется разность фаз на выходе из ячейки, следовательно, меняются параметры эллиптической поляризации света, а, значит, и интенсивность выходящего из поляризатора П2 пучка. При выключенном поле (Е = 0) в силу того, что поляризаторы П1 и П2 скрещены (∆Ф = +π/4 и –π/4 по отношению к вертикали!) световой пучок на выходе равен нулю. Изменение напряженности Е приводит к последовательным просветлениям и затемнениям поля зрения. Например, затемнения наступают при ΔФ = 2πm, или KℓE2 = m .

молекулы в электрическом поле приобретают дипольный момент в направлении поля,

сама молекула при этом ориентируется так, чтобы дипольный момент совпадал с направлением наибольшей поляризуемости молекулы. Отсюда получаем утверждение

– наибольший показатель преломления ( ) оказывается у волны, электрический вектор которой колеблется параллельно внешнему электрическому полю, т.е. у необыкновенной волны:
ne > no , т.к. > , K > 0.

Учёт полярных молекул, т.е. имеющих неравный нулю собственный дипольный момент, усложняет объяснение. Именно у таких веществ проявляются исключения из правил, например, K < 0 . При изменении электрического поля на противоположное (E2 не меняет своего значения) оптические свойства вещества не меняются.
Эффект Керра обладает малой инерционностью (время релаксации ~ 10‑10 c). Это означает, что оптическая анизотропия запаздывает за вызвавшим её электрическим полем на времена порядка 10-10 c. Благодаря этому качеству эффект Керра нашёл широкое применение в технике, например, он позволяет создать быстродействующие модуляторы света.
Обычно размер ячейки Керра выбирают такой, чтобы оптическая разность хода при определённом напряжении составила полволны. Как уже отмечалось, входной и выходной поляризаторы ориентированы так, что их плоскости пропускания скрещены и составляют по 45º (π/4) к направлению электрического поля. При выключенном поле (Е = 0) ячейка не пропускает свет. При включении электрического поля до заданного значения, которому соответствует оптическая разность хода λ/2, свет по известному свойству λ/2- пластинки полностью пройдет через ячейку.

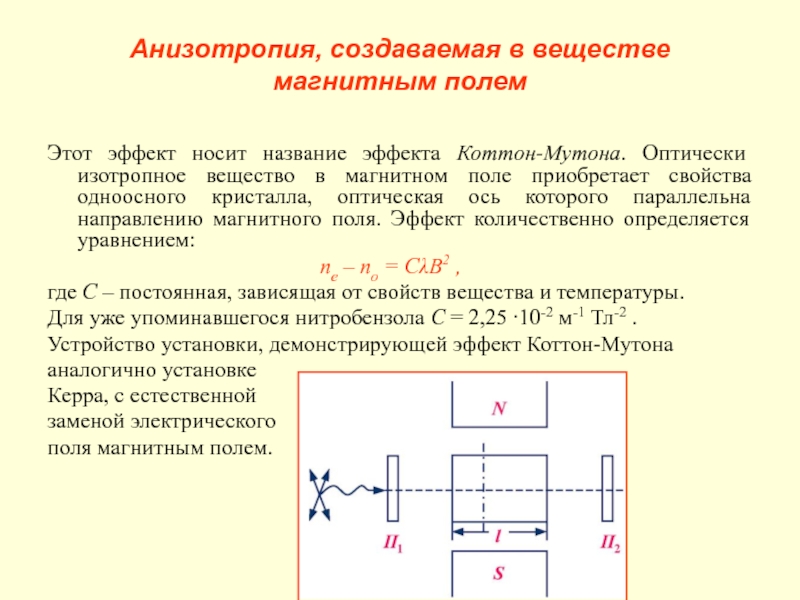
эффекта Коттон-Мутона. Оптически изотропное вещество в магнитном поле приобретает свойства

одноосного кристалла, оптическая ось которого параллельна направлению магнитного поля. Эффект количественно определяется уравнением:
ne – no = СλB2 ,
где С – постоянная, зависящая от свойств вещества и температуры.
Для уже упоминавшегося нитробензола С = 2,25 ∙10-2 м-1 Тл-2 .
Устройство установки, демонстрирующей эффект Коттон-Мутона
аналогично установке
Керра, с естественной
заменой электрического
поля магнитным полем.

линейно поляризованного света через определённые вещества происходит поворот вектора Е

на некоторый угол. Вещества, обладающие такой способностью называются оптически активными.
Оптически активные вещества подразделяются на:
а) кристаллические (кварц),
б) чистые жидкости (никотин, скипидар),
в) растворы оптически активных веществ в неактивных растворителях (водные растворы сахара, винной кислоты и т. д. )
Если на оптически активное вещество направить пучок линейно поляризованного света, то, пройдя через вещество, свет выйдет линейно поляризованным, так что при помощи выходного поляризатора его можно полностью погасить, при этом мы узнаем угол, на который вещество повернуло плоскость его поляризации. Если оптически активное вещество является кристаллическим, например, кварц, следует направить пучок поляризованного света вдоль оптической оси. В этом случае мы убираем эффект двойного лучепреломления, который затруднял бы изучение эффекта оптической активности.

φ вектора поляризации Е. Для этого достаточно дополнительным поворотом выходного

поляризатора П2 установить наибольшую интенсивность выходящего пучка.
Угол доворота поляризатора равен углу поворота φ плоскости поляризации при условии, что оба поляризатора П1 и П2 имели в исходной позиции параллельные плоскости пропускания. Однако более эффективно провести это измерение при скрещенных поляризаторах. Угол поворота φ пропорционален пройденному в оптически активном веществе пути ℓ : φ = α ℓ ,
где α – коэффициент, зависящий от вещества и от длины волны (дисперсия вращательной способности). Для кварцевой пластинки толщиной S мм углы поворота для желтого и фиолетового цвета равны соответственно 100º и 250º , т.е. эффект достаточно сильный. Это соотношение иногда называют законом Био.
В растворах угол поворота φ
пропорционален пройденному
пути и концентрации активного
вещества n: φ = [α] n ℓ , где
[α] – так называемая,
удельная постоянная
вращения.

подразделяют на право- и левовращающие, т.е. по или против часовой

стрелки по отношению к наблюдателю, к которому свет приближается.
Все оптически активные вещества существуют в двух модификациях – право- и левовращающие. Вращательная способность кварца (сильный эффект) связана с его кристаллической структурой, расплавленный кварц теряет это свойство. Структура кристалла кварца отличает правое от левого. Правый кристалл кварца не тождественен левому, но они переходят друг в друга при зеркальном отражении. Итак, только те кристаллы обладают оптической активностью, которые не симметричны при зеркальном отражении (т.е. различают правое и левое). Для оптически активных аморфных тел, жидкостей или растворов эффект вращения обусловлен асимметричным строением молекул (при зеркальном отражении правая молекула переходит в такую же по химическому составу, но не тождественную по оптическим свойствам, левую молекулу).
Важным свойством эффекта является то, что направление вращения (правое или левое) задаётся свойствами молекул вещества, но привязано к направлению луча. Поэтому при прохождении луча света через активную среду, последующего отражения его от зеркала и вторичного прохождения через ту же среду назад, направление линейной поляризации восстанавливается. Таким образом, эффект невозможно «накопить» прогоняя луч света много раз через активную среду туда и обратно с помощью двух зеркал.

поляризации, можно определять концентрацию оптически активных веществ, например, концентрацию сахара

в производственных растворах.
Объяснение эффекта дал Френель, который предположил, что в оптически активных веществах лучи, поляризованные по кругу вправо и влево, распространяются с разными скоростями, следовательно, имеем два показателя преломления: n+ для волн правой поляризации и n- для волн левой поляризации. Линейно поляризованный свет можно представить как суперпозицию двух поляризованных по кругу волн, правой и левой, с одинаковыми частотами и амплитудами. Поскольку вещество (оптически активное) состоит из асимметричных молекул, которые по-разному взаимодействуют с правой поляризацией и с левой, луч света – суперпозиция правой и левой круговых поляризаций, разделяется на два луча (правый и левый), распространяющихся с разными скоростями
( , V+ = , ).

В зависимости от того, какой из лучей окажется более быстрым, на выходе из оптически активной среды, где скорости лучей опять уравняются и поляризация вновь станет линейной, произойдет результирующее отклонение вектора линейной поляризации E, вправо или влево, в соответствии с отношением скоростей V+ и V-.

активными и вращают плоскость поляризации света, распространяющегося в веществе вдоль

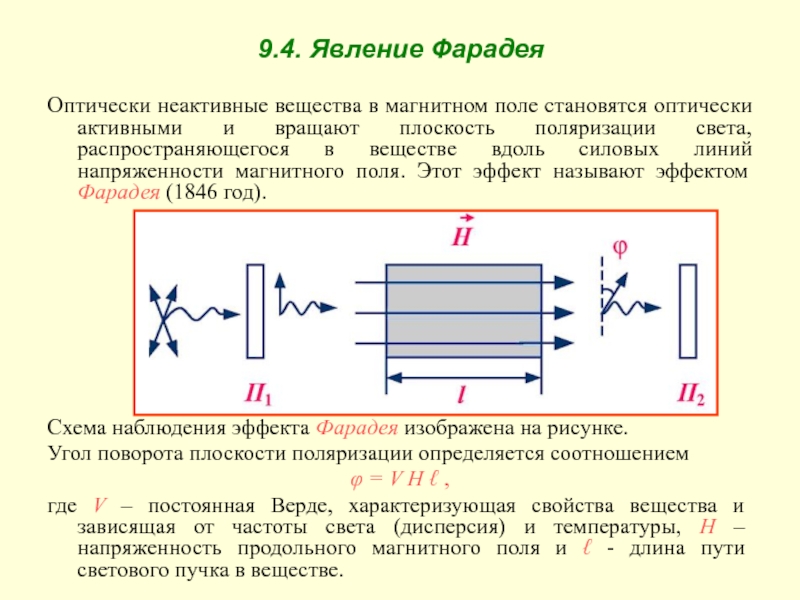
силовых линий напряженности магнитного поля. Этот эффект называют эффектом Фарадея (1846 год).











Схема наблюдения эффекта Фарадея изображена на рисунке.
Угол поворота плоскости поляризации определяется соотношением
φ = V H ℓ ,
где V – постоянная Верде, характеризующая свойства вещества и зависящая от частоты света (дисперсия) и температуры, Н – напряженность продольного магнитного поля и ℓ - длина пути светового пучка в веществе.

направления луча поворот плоскости поляризации не зависит. Эффект можно накопить

(в отличие от естественного вращения), т.е. при отражении луча зеркалом и возвращении его в исходную точку поворот плоскости поляризации удваивается. Это свойство позволяет увеличить угол поворота увеличением длины пути света в веществе за счет многократных отражений от посеребренных поверхностей образца.
Знак вращения принято определять по отношению к направлению магнитного поля H. Для большинства веществ вращение происходит вправо (правый винт вдоль вектора H). Такие вещества называют положительными, к ним относятся все диамагнетики. Имеются и отрицательные вещества, которые обязательно содержат парамагнитные атомы. Углы поворота
φ невелики. Для большинства
твердых тел при напряженности
порядка 106 А/м и ℓ ~ 10 см угол
поворота составляет 1÷2º, для газов
значительно меньше.

что испускание света атомом связано с движением его электронов, а

позднее дал возможность детально и с высокой точностью проверить правильность квантовой механики. В 1896 г. голландский физик Зееман обнаружил, что спектральные линии веществ расщепляются, если источник света помещен в магнитное поле. Зееман исследовал зелено-голубую линию кадмия в магнитном поле с напряженностью (1,0 – 1,5) Гс.
Источник света с линейчатым спектром помещен между полюсами электромагнита. Исследуемый свет попадает на вход спектрографа или спектроскопа с высокой разрешающей силой (порядка и выше). Николи N и пластинка λ/4 используются для исследования
поляризации излучаемого
света. В качестве источника
света используется
газоразрядная трубка
или вакуумная дуга.

расщепляется на три линейно поляризованные компоненты. Средняя компонента не смещена,

крайние смещены симметрично в противоположные стороны на одинаковые расстояния в шкале частот. Смещение пропорционально напряженности внешнего магнитного поля, вызывающего расщепление. В средней компоненте поляризация направлена параллельно магнитному полю (так называемая π- компонента), в крайних – перпендикулярно полю (σ-компоненты). Интенсивность π- компоненты составляет половину от интенсивности исходной линии, каждая из σ- компонент имеет интенсивность, составляющую одну четвертую исходной. На рисунке приведено схематическое изображение спектральной картины, причем высота линий показывает в линейном масштабе интенсивность спектральных линий: а – спектральная линия в отсутствие магнитного поля, б – поперечный эффект, в – продольный эффект.

симметрично расположенные в шкале частот, σ- компоненты имеют интенсивность вдвое

меньшую интенсивности исходной спектральной линии. Обе компоненты поляризованы по кругу в противоположных направлениях, причем в случае распространения света вдоль направления магнитного поля компонента с меньшей частотой (σ–компонента) поляризована по правому, а с большей (σ+—компонента) по левому кругу. При изменении направления магнитного поля на противоположное, то есть в случае распространения луча против направления магнитного поля, на противоположное меняется и круговая поляризация обеих компонент. В этом случае принято говорить, что в продольном эффекте Зеемана σ–компонента поляризована по правому кругу по отношению к направлению магнитного поля независимо от направления распространения луча, т.е. круговая поляризация σ– компоненты соответствует правому винту, где за направление движения винта принимается
направление линий магнитного поля.

как квазиупруго связанных электронов с массивным ядром. Собственные частоты колебаний

электронов определяют спектральные линии излучения атома. В отсутствие внешнего поля уравнение движения электрона имеет вид где ω0 - собственная частота электрона. Включение магнитного поле приводит к
появлению добавочной силы Лоренца

тогда:

Введем вектор называется ларморовской частотой
Тогда:

Направим ось Z вдоль направления магнитного поля, тогда уравнение движения будет:



Введем комплексную переменную ς: ς = x + iy.
Получаем линейное однородное дифференциальное уравнение в комплексной плоскости:

Ω ~ 1011 Гц, то
Тогда имеем два линейно независимых решения

дифференциального уравнения

Первое решение описывает вращение электрона в плоскости XY с частотой в положительном направлении, т.е. против часовой стрелки, второе решение описывает вращение электрона с частотой в отрицательном направлении, т.е. по часовой стрелке.

Смысл полученного общего решения следующий. Колебания электрона в плоскости перпендикулярной направлению магнитного поля можно представить как комбинацию с произвольными весовыми коэффициентами вращательных движений: вращения против часовой стрелки (положительное), происходящее с частотой ω1 = ω0 + Ω, и вращения по часовой стрелке (отрицательное), происходящее с частотой ω2 = ω0 – Ω. Направление вращений определяются по отношению к наблюдателю, расположенному навстречу линиям магнитного поля.

максимально в направлении, перпендикулярном ускорению электрона и равна нулю в

параллельном направлении.
При наблюдении поперек индукции магнитного поля колебания электрона, параллельные полю, дают максимальную индикатрису излучения, но они имеют несмещенную частоту. Поляризация соответствующего излучения π-компоненты будет, как и вызвавшие ее колебания электрона направлена вдоль индукции магнитного поля. Оба круговых движения, правое и левое, совершаются в плоскости, перпендикулярной внешнему полю. Только колебания, перпендикулярные к линии наблюдения, сопровождаются излучением с максимальной индикатрисой и дают две σ-компоненты с частотами ω1 и ω2, в которых векторы поляризации перпендикулярны индукции магнитного поля. Колебания вдоль линии наблюдения не наблюдаются.
При наблюдении вдоль магнитного поля колебание в том же направлении не посылает излучение, поэтому несмещенная π-компонента отсутствует. В результате наблюдаются две σ-компоненты с круговой поляризацией.
При поперечном эффекте колебания вдоль линии наблюдения (для определенности назовем ее осью Y) не наблюдаемы, наблюдаемы колебания вдоль осей X и Z, независимо от того, включено поле или нет. При включенном поле колебания вдоль оси Z ответственны за несмещенную σ-компоненту с интенсивностью, равной половине исходной интенсивности. Вторая половина интенсивности, связанная с колебаниями вдоль оси X
В продольном эффекте наблюдаемы только колебания электрона вдоль осей X и Y, которые при включенном поле структурируются во вращательные движения с частотами ω1 и ω2.

Зеемана наблюдается и на линиях поглощения. Вещество в газообразном агрегатном

состоянии, например, пары металла, имеющее резкую спектральную линию поглощения помещают в сильное однородное магнитное поле. Пропуская мощный световой поток через абсорбирующее вещество, наблюдают расщепление линии поглощения при включении магнитного поля. При продольном наблюдении после появления магнитного поля линия поглощения заменяется двумя линиями, сдвинутыми симметрично в область больших и меньших частот, при этом величина сдвига пропорциональна магнитной индукции. При поперечном наблюдении исходная линия поглощения сопровождается двумя другими, расположенными симметрично по обе стороны от нее. Величина расщепления крайних компонент совпадает с аналогичным расщеплением в продольном эффекте, при этом коэффициент поглощения зависит от поляризации падающего света. Рассмотренный эффект получил название обратного эффекта Зеемана.

частоты распространяющейся волны к собственным частотам вещества (кривая дисперсии). Под

действием продольного магнитного поля изменяются собственные частоты атомов, соответствующие правому и левому вращению, смещение происходит симметрично в шкале частот на величину, пропорциональную индукции магнитного поля. Следовательно, под действием магнитного поля изменяется и показатель преломления, причем различно для волн, поляризованных по правому и левому кругу. Разным значениям показателя преломления соответствуют разные значения фазовых скоростей. Под действием магнитного поля возникает двойное, по признаку правое или левое, вращательное преломление, то есть, в конечном итоге, вращение плоскости поляризации продольным магнитным полем – явление Фарадея. На рисунке кривая I показывает зависимость показателя преломления в продольном магнитном поле для волны, поляризованной по левому кругу, а кривая II – зависимость показателя преломления для волны,
поляризованной по правому
кругу, сплошная кривая
показывает зависимость
показателя преломления в
отсутствие магнитного
поля.

ω0 – Δω = ω0 – Ω = ω1 для

волны, поляризованной по левому кругу, и ω0 + Δω = ω0 + Ω = ω2, для волны поляризованной по правому кругу.
Из рисунка видно, что для любой частоты ω, не принадлежащей интервалу ω0 – Δω < ω < ω0 + Δω, nI > nII. Следовательно, скорость волны, поляризованной по правому кругу, превосходит скорость волны, поляризованной по левому кругу, при всех значениях частоты , кроме указанного интервала. Отсюда следует результат Фарадея: при распространении света в прозрачной не поглощающей среде в продольном магнитном поле происходит вращение плоскости поляризации световой волны вправо по отношению к направлению магнитного поля. Вращение плоскости поляризации определяется только направлением магнитного поля и не зависит от направления распространения световой волны.
В области полосы поглощения, т.е. вблизи собственных частот вещества, помимо аномальной дисперсии происходит и аномальное магнитное вращение плоскости поляризации, именно: при ω0 – Δω < ω < ω0 + Δω знак вращения отрицателен, т.е. вращение происходит влево. Аномальное поведение плоскости поляризации называют эффектом Макалюзо и Корбино (1898).

при воздействии сильного электрического поля на источник излучения. Поле может

быть либо внешним по отношению к источнику, либо внутренним, создаваемым соседними атомами или ионами. Эффект назван по имени Й. Штарка, впервые наблюдавшего его в 1913. Он аналогичен эффекту, обнаруженному П. Зееманом в 1896 и состоящему, как было выяснено, в расщеплении спектральных линий магнитным полем. Эффект Штарка обусловлен тем, что под действием электрического поля облако электронов, окружающих ядро излучающего атома, изменяет свое положение относительно ядра. В результате изменяются энергетические уровни электронов в атоме. Поскольку свет испускается при переходе электрона с одного энергетического уровня на другой, изменение энергетических уровней приводит к изменению спектра испускаемого света. Эффект Штарка – одно из наиболее убедительных подтверждений квантовой теории строения вещества. Классической теории эффекта Штарка не существует. Эффект имеет последовательное непротиворечивое объяснение только в рамках квантовой теории.