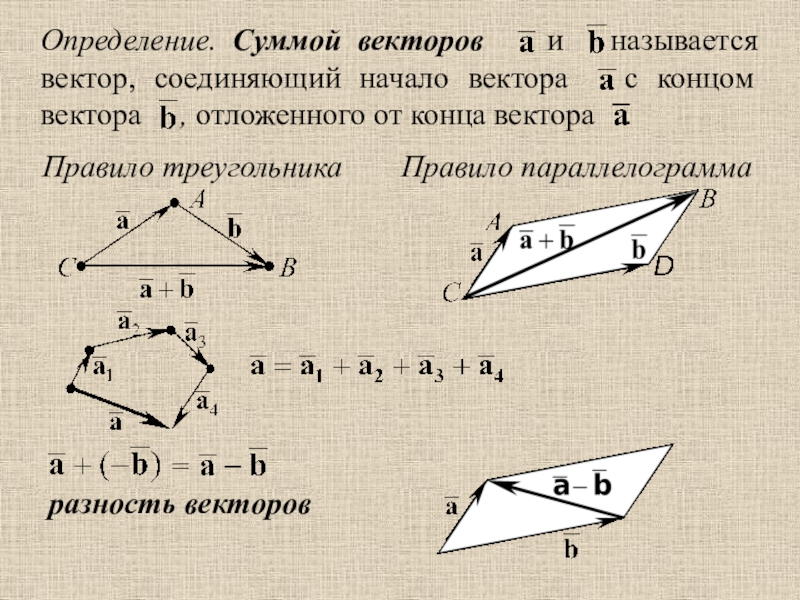
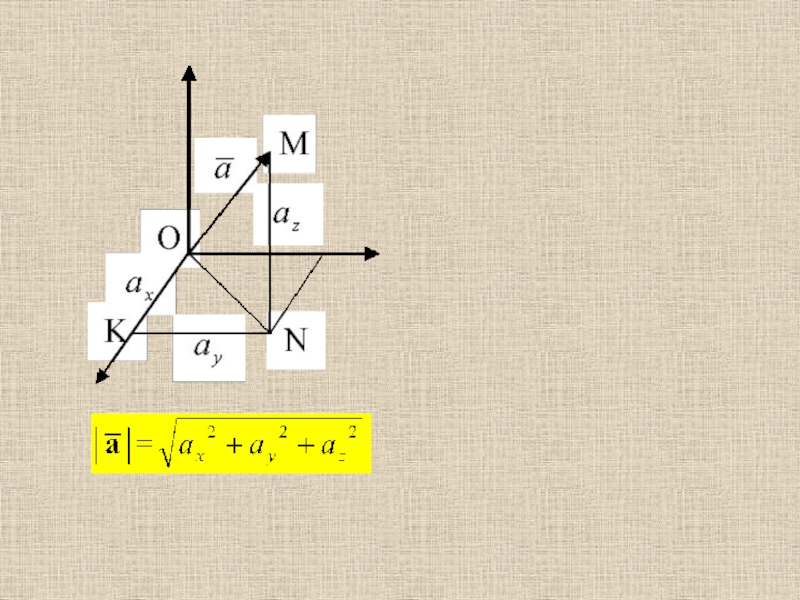система координат
Скалярное произведение векторов
Свойства скалярного произведения
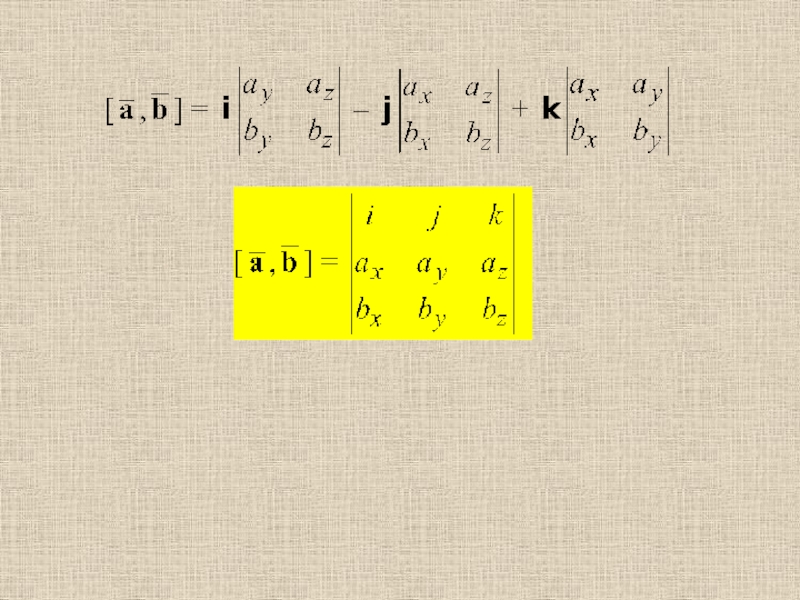
Векторное произведение
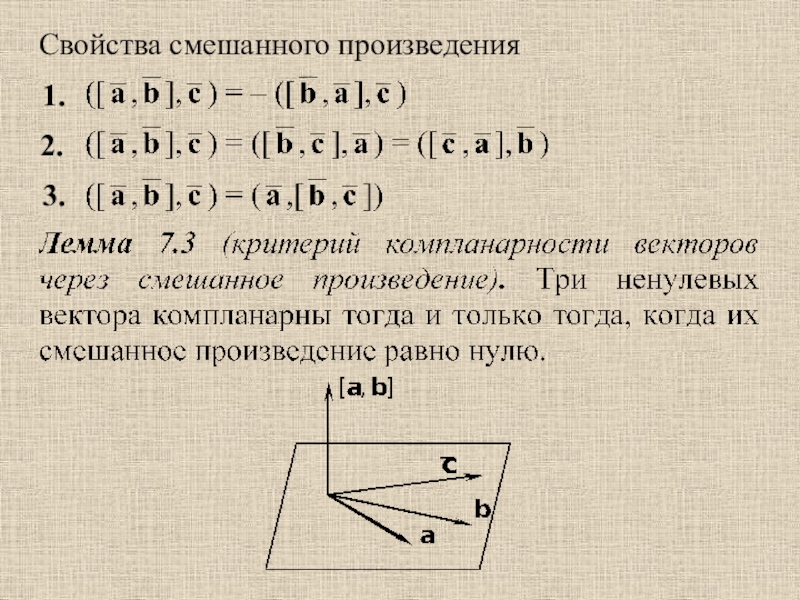
Смешанное произведениеСвойства смешанного произведения