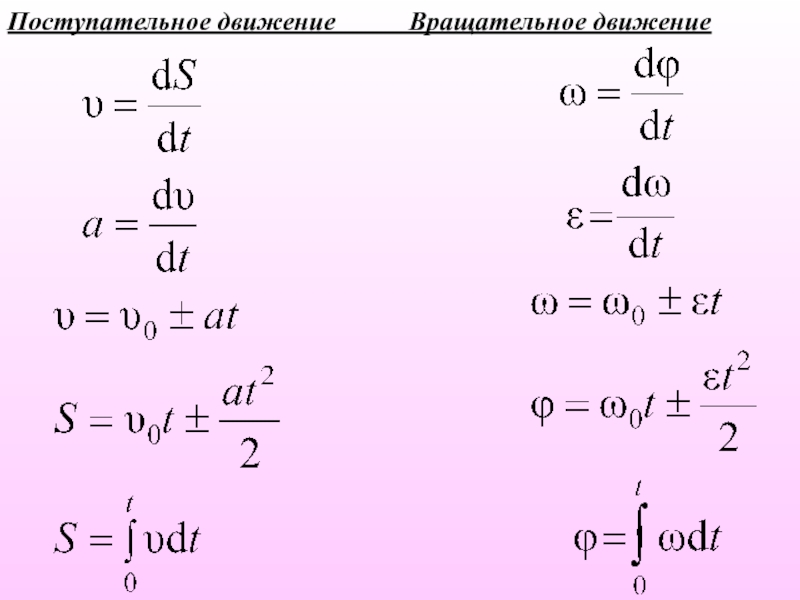Лекция № 6 ДИНАМИКА ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

точки.
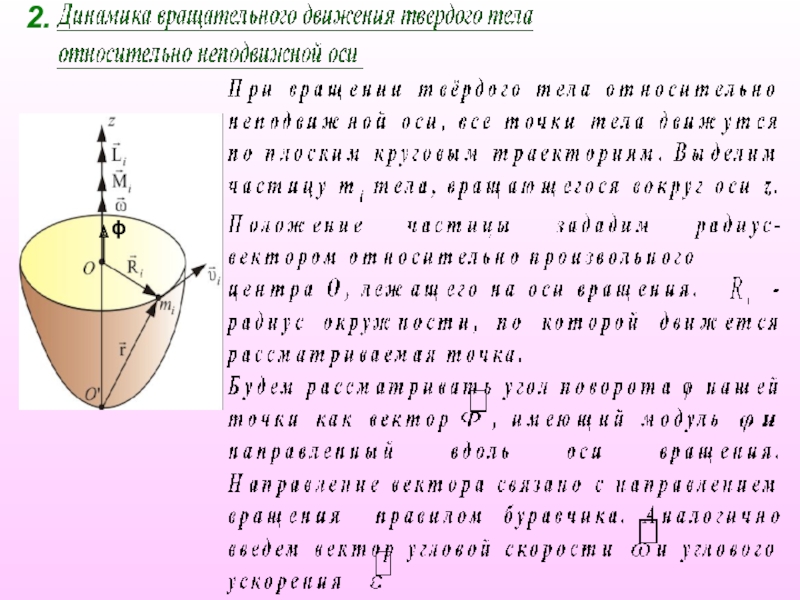
2. Динамика вращательного движения относительно
неподвижной оси.
3. Расчет моментов

инерции некоторых простых тел.
Теорема Гюйгенса-Штейнера.
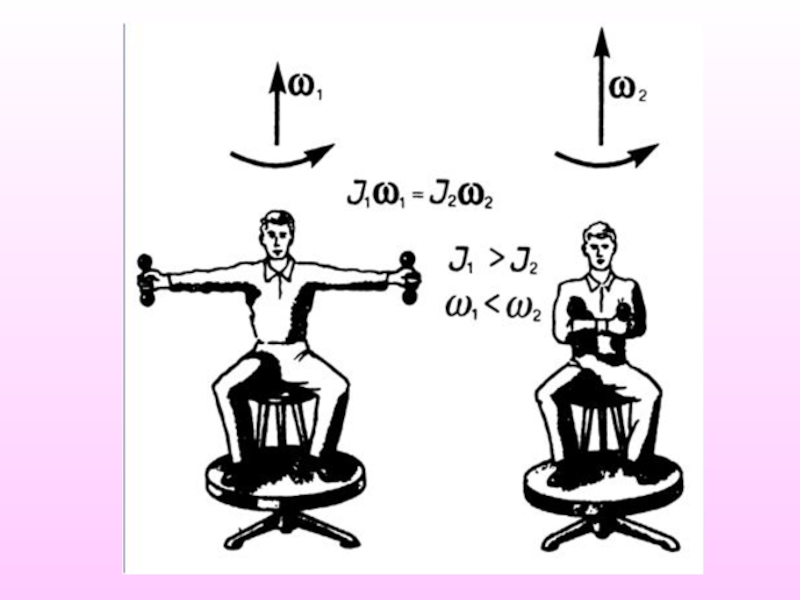
4. Закон сохранения момента импульса.
5. Кинетическая энергия твердого тела
6. Произвольное движение твердого тела.
7. Скатывание цилиндра с наклонной плоскости.
8. Сходство и различие линейных и угловых характеристик движения.
.

– это система материальных точек, расстояния между которыми сохраняются независимо

от внешних воздействий. Иными словами в твердом теле отсутствует относительное движение этих точек.
Рассмотрим твердое тело, как некую систему, состоящую из n точек (m1 m2 … mn); ri – радиус-вектор i-ой точки,
проведенный из точки О – неподвижного центра вращения.
обозначения:
- внешняя сила, действующая действующая на
на i-ю точку,
- сила, действующая со
стороны k-ой точки на i-ую точку

можно вынести за знак векторного произведения (и знак суммы тоже),

тогда:

Запишем основное уравнение динамики для точки:

n уравнений для всех точек системы и сложим, левые и

правые части уравнений:

Так как , то

-

суммарный момент импульса
твердого тела.

Обозначим - результирующий
момент всех внешних
сил относительно неподвижной точки О.

Окончательно получим:

точки.


Уравнение моментов относительно неподвижной точки
Векторное уравнение можно представить в

скалярном виде , если спроецировать и на оси координат x, y, z:

Написанные уравнения – уравнения моментов
относительно неподвижных осей.

Имеет внешнее сходство с уравнением
динамики для поступательного движения:

всех его материальных точек
Момент импульса Li любой точки равен
Li =

mirivi = miriri = miri2

.

Ранее мы получили, что = I, поэтому окончательно



Для сравнения, в случае поступательного движения

 

 

момент инерции тонкого однородного стержня относительно оси z, проходящей через

его центр масс — точку С. Длина стержня — l, его масса — M.
На расстоянии x от оси вращения выделим элемент dx, масса которого

Момент инерции этой частицы стержня равен:

взяв интеграл:




получаем
Моменты инерции некоторых тел

момента инерции Ic относительно оси, параллельной данной и проходящей через

центр масс тела, и произведения массы тела М на квадрат расстояния между осями:
I = Ic + Ma2

При вычислении момента инерции тела, вращающегося вокруг оси, не проходящей через центр инерции, следует пользоваться теоремой о параллельном переносе осей или теоремой Гюйгенса - Штейнера :

Теорема Гюйгенса-Штейнера

а

проходящей через конец стержня (рис).

в виде:
Оно в равной степени справедливо как для твердого

тела, так и для системы тел. Если момент внешних сил относительно оси z равен нулю, то момент импульса системы относительно этой же оси будет оставаться постоянным.

Это закон сохранения момента импульса — аналог закона сохранения импульса.

означает постоянства угловой скорости:
если момент инерции вращающегося тела меняется, то

будет меняться его угловая скорость даже в случае отсутствия внешних вращающих моментов. При этом сохранится неизменным произведение
Iz   = сonst, то есть угловая скорость окажется обратно пропорциональной моменту инерции тела (системы):

Известно много примеров, иллюстрирующих эту особенность закона сохранения момента импульса: вращение фигуристов и балерин, опыты на скамье Жуковского и т.п.

вращающегося вокруг неподвижной оси z с угловой скоростью , суммируя

кинетические энергии бесконечно малых элементов тела

КК

где J – момент инерции тела относительно оси вращения тела, vi = riωi - линейная скорость элемента тела с массой mi .

Сравним с формулой для кинетической энергии поступательного движения
K = mv2/2

твердого тела – плоское движение. Это движение , при котором

все точки тела остаются в параллельных плоскостях. Примером такого движения является качение цилиндра по горизонтальной или наклонной плоскостям.

Пусть тело движется под действием некоторой системы внешних сил. Эту систему внешних сил можно всегда привести к центру масс тела О и заменить результирующей силой , приложен-
ной в точке О, и суммарным моментом внешних сил относительно этой же точки

тела, принимает вид:
где m - масса тела

- скорость движения центра масс тела и
- момент импульса тела относительно его центра масс.

движения центра масс и вращательное движение с угловой скоростью описывается выражением:

Здесь I0 – момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.

из уравнений движения, и два кинематических условия

Сплошной цилиндр
массы m и радиуса R
скатывается без
проскальзывания с
наклонной
плоскости. Угол
наклона плоскости –
, а высота Н (Н » R). Начальная скорость цилиндра равна нулю. Определим скорость центра масс цилиндра у основания наклонной плоскости.

сила тяжести
упругая сила реакции
опоры

и
сила трения покоя
, т.к. качение
без проскальзывания

Представим это движение суммой двух движений: поступательного со скоростью VC , с которой движется ось цилиндра, и вращательного вокруг оси цилиндра с угловой скоростью .

правда, присутствует сила трения, но её работа равна нулю, поскольку

точка приложения этой силы в процессе спуска остаётся неподвижной: ведь движение происходит без проскальзывания. Раз нет работы силы трения, механическая энергия системы не меняется.

и в конце спуска. Полная энергия цилиндра в этих положениях

одинакова:

Так как , а , получаем:




Отсюда легко найдем конечную скорость цилиндра


.

скоростью центра масс:


Продифференцировав это уравнение по времени, получим соотношение для

ускорений:

или

Воспользовавшись теоремой о движении центра масс, опишем поступательное движение цилиндра:

Если стоит задача нахождения времени скатывания цилиндра, то для решения нужно воспользоваться уравнением моментов

скалярных уравнения:
x: mgSin – Fтр = maC

(1)
y: N – mgсos = 0 (2)
Для описания вращения воспользуемся основным уравнением динамики вращательного движения:
MC = IC   ( )

Из трёх названных сил момент относительно оси цилиндра создаёт только сила трения:

совместно уравнения движения(1), (2), и (3) получим следующие значения неизвестных

величин:

Из выражения для следует, что с увеличением угла наклона  должна возрастать и сила трения покоя Fтр.

неравенство:

⅓mgSin ≤ mgCos.

Отсюда следует, что скатывание будет происходить без проскальзывания до тех пор, пока угол  не превзойдёт значения пред:
пред = arctg3.
Здесь  — коэффициент трения цилиндра по плоскости.

При таком движении без начальной скорости цилиндр достигнет основания наклонной

плоскости за время:
длина наклонной
, где плоскости


Так как , то время скатывания:

полученным выше более простым путем, исходя из закона сохранения энергии.

динамики вращательного движения легко запоминаются, если сопоставить их с формулами

поступательного движения.
Отмечу, что в приведенной ниже таблице
рассмотрены случаи движения с постоянными ускорениями: