Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №7 Асимметричное шифрование
Содержание
- 1. Лекция №7 Асимметричное шифрование
- 2. Асимметричные криптосистемы (системы открытого шифрования, с открытым
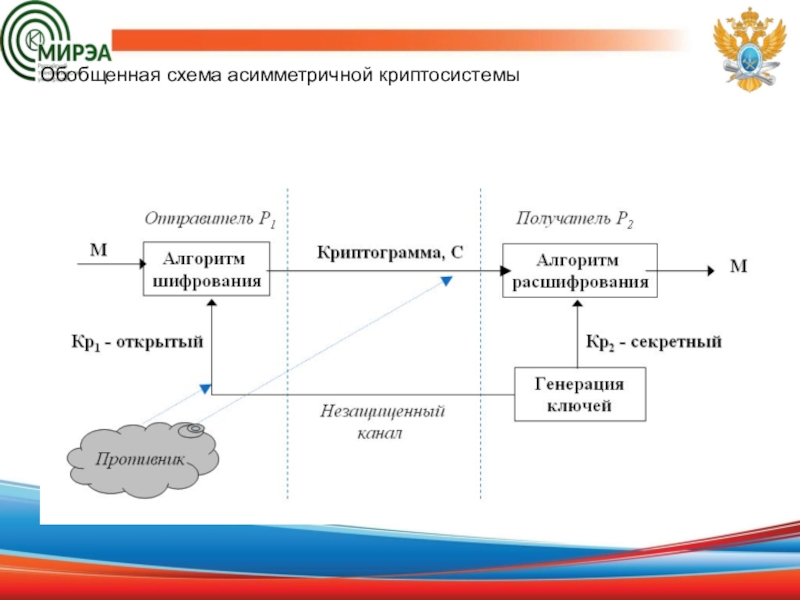
- 3. Обобщенная схема асимметричной криптосистемы
- 4. В настоящий момент во многих асимметричных криптосистемах
- 5. Расшифровать сможет только упомянутый пользователь с секретным
- 6. Методы проверки чисел на простоту Одна из
- 7. Поэтому уже для чисел порядка
- 8. Обычно эти условия основаны на малой теореме
- 9. ПримерЕсли требуется определить, является ли целое число
- 10. Если равенство не выполнено, то на основании
- 11. К сожалению, существуют так называемые числа Кармайкла
- 12. Классический результат теории чисел – теорема Чебышева
- 13. Спасибо за внимание
- 14. Скачать презентанцию
Асимметричные криптосистемы (системы открытого шифрования, с открытым ключом - public key systems) – смысл данных криптосистем состоит в том, что для зашифрования и расшифрования используются разные преобразования. Одно из них –
Слайды и текст этой презентации
Слайд 4В настоящий момент во многих асимметричных криптосистемах вид преобразования определяется
ключом. У пользователя есть два ключа – секретный и открытый.
Открытый ключ публикуется в общедоступном месте, и каждый, кто захочет послать сообщение этому пользователю – зашифровывает текст открытым ключом.Слайд 5Расшифровать сможет только упомянутый пользователь с секретным ключом. Таким образом,
отпадает проблема передачи секретного ключа, как в симметричных системах. Однако,
несмотря на все свои преимущества, эти криптосистемы достаточно трудоемки и медлительны. Стойкость асимметричных криптосистем базируется, в основном, на алгоритмической трудности решить за приемлемое время какую-либо задачу. Если злоумышленнику удастся построить такой алгоритм, то дискредитирована будет вся система и все сообщения, зашифрованные с помощью этой системы. В этом состоит главная опасность асимметричных криптосистем в отличие от симметричных.Слайд 6Методы проверки чисел на простоту
Одна из главных проблем асимметричного
шифрования – генерация больших простых чисел. Простейшим методом проверки простоты
натурального числа N является метод пробных делений: для d=2, 3, 4 … мы проверяем выполнение условия (d, N)>1 (здесь (d, N) – наибольший общий делитель чисел d и N). Число операций, требуемых для этого метода, имеет порядок корня из N.Слайд 7Поэтому уже для чисел порядка он не применим.
В отличие от таких “детерминированных“ тестов существуют еще “вероятностные“ тесты
проверки простоты. Для исследуемого числа проверяется выполнение некоторых, связанных со случайными числами, условий. Если какое- либо из этих условий не выполнено, то N – составное число. Если же все условия выполнены, то с некоторой вероятностью можно утверждать, что N – простое число. Эта вероятность тем ближе к 1, чем большее количество случайных чисел мы проверим. Слайд 8Обычно эти условия основаны на малой теореме Ферма, утверждающей, что
для любого положительного числа b, не превосходящего некоторого простого числа
p :Слайд 9Пример
Если требуется определить, является ли целое число r простым, то
можно выбрать любое положительное целое число b, меньшее r, и
проверить, выполнено ли равенствоСлайд 10Если равенство не выполнено, то на основании теоремы Ферма можно
быть совершенно уверенным, что r – не простое число. Если
же равенство выполнено, то можно лишь предполагать, что r – простое число и поэтому назвать его “псевдопростым по основанию b“. Вероятность P (x) того, что составное число x окажется псевдопростым по случайному основанию, убывает с ростом x.Слайд 11К сожалению, существуют так называемые числа Кармайкла – такие составные
числа, которые обладают свойством:
Пример числа Кармайкла
561 = 3*11*17
Слайд 12Классический результат теории чисел – теорема Чебышева – показывает, что
доля положительных целых чисел, меньших некоторого целого m и являющихся
простыми, близка к 1/(ln m). Например, доля целых чисел, меньших и являющихся простыми, близка к 1/(ln ) = 1/230.Таким образом, если мы выберем случайно большое целое положительное нечетное число x и будем последовательно проверять на простоту числа x, x+1, x+2, … , то, в среднем, мы впервые встретим простое число на шаге с номером ln x.