Слайд 1ЛОГИКА БУЛЯ
Булевы переменные и булевы функции
Слайд 2Возвращаясь к диаграмме Эйлера-Венна для двух множеств , с точки
зрения логики, вместо одной предметной переменной х удобно ввести две
логические переменные а и b, определяемые областями множеств соответственно А и В.
Эти переменные могут принимать только два логических значения: 1 – истина, т.е. принадлежность множеству, или 0 – ложь.
Тогда подмножества С0, С1, С2 и С3 определят следующие значения логических переменных: С0 - а = 0, b = 0; С1 - а = 1, b = 0; С2 - а = 0, b = 1; С3 - а = 1, b = 1.
С0
С1
С2
С3
Слайд 3Аппарат логики Буля оперирует с логическими (Булевыми) переменными, которые могут
принимать только два значения:
0 и 1.
Логические переменные определяют
некую логическую зависимость, которую принято называть булевой функцией.
Множество всех булевых функций и операций над ними образует булеву алгебру или алгебру логики.
Булевы функции могут принимать тоже только два взаимно исключающих значения 0 и 1.
Логические величины 0 и 1 нельзя трактовать как числа, над ними нельзя производить арифметические действия, поскольку алгебра логики – это не алгебра чисел, а алгебра состояний.
Слайд 4Основные логические действия соответствуют простейшим операциям над множествами, это:
инверсия,
или отрицание,
дизъюнкция, или логическое сложение,
конъюнкция, или логическое умножение.
На основании этих трех логических действий строятся все сколь угодно сложные логические функции.
Слайд 5При этом следует особо выделить функции одной и двух переменных,
которые играют в алгебре Буля весьма важную роль.
При помощи
этих функций, используя принцип суперпозиции, можно описать любую логическую функцию любой сложности любого числа переменных.
Принцип суперпозиции заключается в том, что каждый аргумент логической функции может являться функцией других логических переменных, а именно: если есть функция ,
то возможно, что
.
Слайд 6Булевых функций одной переменной всего четыре.
Нулевая (const”0”)
– значение функции равно нулю, каким бы ни было значение
входной переменной.
Инверсия (не) – значение функции инверсно значению входной переменной.
Повторение (да) – значение функции повторяет значение входной переменной.
Единичная (const”1”) – значение функции равно единице при любом значении входной переменной.
Слайд 7Функции двух переменных
1.
- конъюнкция, логическое «и»;
2. - дизъюнкция, логическое «или»;
3. - штрих Шеффера, логическое «и-не»;
4. - стрелка Пирса (функция Вебба), логическое «или - не»;
5. - запрет b, «а, но не b»
6. - импликация b, «если а, то b»
«b, но не а»
8.
- импликация а, «если b, то а»
9.
- эквивалентность, равнозначность
10.
- неравнозначность, «сумма по модулю 2».
Слайд 9Из всех функций двух переменных десять являются самостоятельными и зависят
как от переменной а, так и от переменной b.
Притом
функции Y5 ,Y6 отличаются от соответствующих им Y7 ,Y8 лишь порядком расположения аргументов.
Таким образом, лишь восемь из 16-ти булевых функций двух переменных являются оригинальными.
Слайд 10Постулаты (аксиомы) логики Буля
Если x ≠ 1, то
= 0; если x = 0, то =
1 (аксиома взаимоисключения);
0 0 = 0; 0 0 = 0;
0 1 = 0; 0 1 = 1; (1 0 = 0; 1 0 = 1);
1 1 = 1; 1 1 = 1;
; (инверсии);
; (двойной инверсии).
Слайд 11В качестве основных законов алгебры Буля чаще других используют следующие
:
Нулевого множества:
0 ∧ a = 0; 0
∧ a ∧ b ∧ … ∧ x= 0; 0 ∨ a = a
2. Универсального множества:
1 ∧ a = a; 1 ∨ a = 1; 1 ∨ a ∨ b ∨ c ∨ … ∨ x = 1;
3. Идемпотентности (повторения):
a ∨ a ∨ a ∨ … ∨ a = a; a ∧ a ∧ a ∧ … ∧ a = a;
4. Дополнительности (противоречия):
a ∧ a= 0; a ∨ a = 1;
=
5. Двойной инверсии: а = a ;
Слайд 126. Коммутативности(переместительный):
a ∨ b = b ∨
a; a ∧ b =
b ∧ a;
7. Ассоциативности (сочетательный):
a ∨ (b ∨ c) = (a ∨ b) ∨ c;
a ∧ (b ∧ c) = (a ∧ b) ∧ c;
8. Дистрибутивности
(распределительный):
a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c);
9. Поглощения:
a ∨ (a ∧ b) = a; a ∧ (a ∨ b) = a;
Слайд 1310. Склеивания:
(a ∧ b) ∨ (a ∧b) = a;
(a ∨ b) ∧ (a ∨b) = a
;
a ∧ (a∨ b) = a ∧ b; a ∨ (a ∧ b) = a ∨ b ;
11. Инверсии (теорема де-Моргáнa):
a ∧ b ∧ c =a ∨ b ∨ c;
a ∨ b ∨ c =a ∧ b ∧ c;
12. Теорема Шеннона: для того, чтобы получить инверсию некоторой ФАЛ, необходимо взять инверсии переменных и заменить операции дизъюнкции на конъюнкции и наоборот:
если существует Y = f (a,b,c,...,x, ∧, ∨),
то Y = f (a,b,c,...,x, ∧, ∨).
Слайд 1413. Разложения:
f (a, b, c,..., x) =
[a ∧
f (1,b,c,...,x)] ∨ [a∧ f (0,b,c,...,x)];
f (a, b, c,..., x)
=
[a ∨ f (0,b,c,...,x)] ∧ [a ∨ f (1,b,c,...,x)].
Законы и теоремы булевой алгебры необходимы для преобразования и упрощения логических функций, для доказательства тождественности и равносильности функций, а также для представления булевых функций в различных формах.
Слайд 15Формы представления булевых функций
Элементарная конъюнкция (дизъюнкция) – это логическое произведение
(сумма) любого числа независимых логических переменных, входящих в нее с
инверсией или без инверсии не более одного раза. Число входных переменных называется рангом элементарной конъюнкции (дизъюнкции).
Соседними называются элементарные конъюнкции (дизъюнкции) одного и того же ранга, содержащие одни и те же переменные, но отличающиеся знаком инверсии одной из переменных.
Слайд 16Дизъюнкция любого числа элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ),
например:
(a ∧ b ∧c )∨(b ∧ c )∨d илиa
bc +b c +d .
Конъюнкция любого числа элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ), например:
(a ∨ b ∨c ) ∧ (a ∨c ∨ d) ∧ (b ∨d )
или (a + b + c ) (a +c + d) (b +d )
(далее для упрощения восприятия булевых функций будем использовать второй вид записи).
Слайд 17Теоремы разложения можно применить ко всем переменным, определяющим булеву функцию,
тогда, например, используя первую теорему разложения для функции трех переменных
f(a,b,c), получим:
f(a,b,c) = a · b · c · f(1,1,1) +a ·b · c· f (0,1,1) + a·b· c · f(1,0,1) + a · b·c · f(1,1,0) +a ·b · c · f(0,0 ,1) + a ·b·c · f(0,1,0 ) + a·b ·c · f(1,0,0) +a ·b ·c · f(0,0,0).
Нетрудно заметить, что по закону нулевого множества элементы с нулевым значением функции обратятся в ноль и останутся лишь наборы переменных при единичном значении функции, которые далее будем называть конституентами разложения единицы, или минтермами.
Слайд 18Разложения функции на конституенты нуля:
f(a,b,c)=[a + b + c +
f(0,0,0) ]·[a + b + c + f(1,0,0)]· [a+b +c
+ f(0,1,0]·[a + b+c +f(0,0,1)]·[a +b +c + f(1,1,0)] ·[a + b +c +f(1,0,1)]·[a+b +c + f(0,1,1)] ·[a +b +c f(1,1,1)].
Здесь, по закону универсального множества, каждая элементарная дизъюнкция с единичным значением функции принимает также единичное значение, и в результате остаются только те дизъюнкции переменных, инверсные значения которых определяют нулевое значение функции. Эти дизъюнкции называются конституентами разложения нуля, или макстермами.
Слайд 19Раскладывая булевы функции на конституенты, мы получаем совершенные формы представления
функций. Таким образом, совершенной дизъюнктивной формой (СДНФ) называется дизъюнкция конституентов
единицы (минтермов), а совершенной конъюнктивной формой (СКФ) конъюнкция конституентов нуля (макстермов).
Слайд 20Для перехода из ДНФ в СДНФ необходимо следующее:
1. Ввести недостающие
переменные в каждую конъюнкцию умножением ее на дополнительность вида (х
+x), где х – недостающая переменная.
2. Раскрыть скобки.
3. Избавиться от повторяющихся конъюнкций на основании закона повторения.
Например: Y =a ·b ·c + b · c +a =a ·b ·c + b·c ·(a +a ) + ·(b +b )·(c +c ) =a ·b ·c + a · b · c +
a · b · c +a · b · c +a ·b · c +a ·b ·c +a ·b ·c =a ·b ·c + a · b · c + a ·b · c +a ·b·c +a ·b ·c +a ·b ·c.
Слайд 21Алгоритм перехода из КНФ в СКНФ
1. Ввести недостающие переменные в
каждую дизъюнкции, используя закон дополнительности х ·x = 0, где
х – недостающая переменная.
2. Произвести преобразования, используя законы ассоциативности и дистрибутивности:
a + (b · c) = (a + b) · (a + c).
3. Избавиться от повторяющихся дизъюнкций на основании закона повторения.
Например:
Y = (a+b+c)·(a +b )·a = (a+b+c)·(a +b + c·c) (a + b ·b + c·c ) = (a + b + c)·(a +b + c)· (a +b +c )·(a + b + c·c)(a + b + c·c) = (a+b+c)· (a +b + c) ·(a +b +c )
(a + b + c)·(a +b+c)· (a +b + c) ·(a +b +c ) = (a + b + c)·(a +b + c)·(a +b +c )·(a + b + c)·(a + b +c).
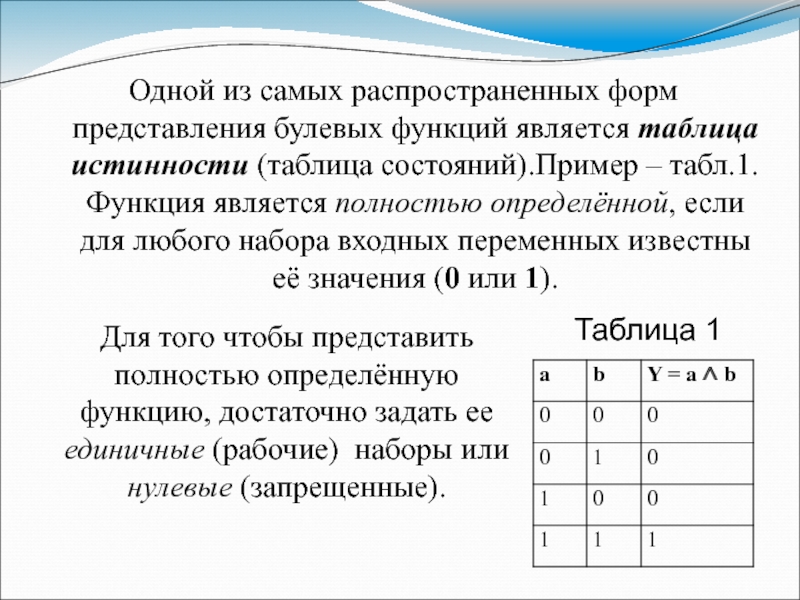
Слайд 22Одной из самых распространенных форм представления булевых функций является таблица
истинности (таблица состояний).Пример – табл.1. Функция является полностью определённой, если
для любого набора входных переменных известны её значения (0 или 1).
Для того чтобы представить полностью определённую функцию, достаточно задать ее единичные (рабочие) наборы или нулевые (запрещенные).
Таблица 1
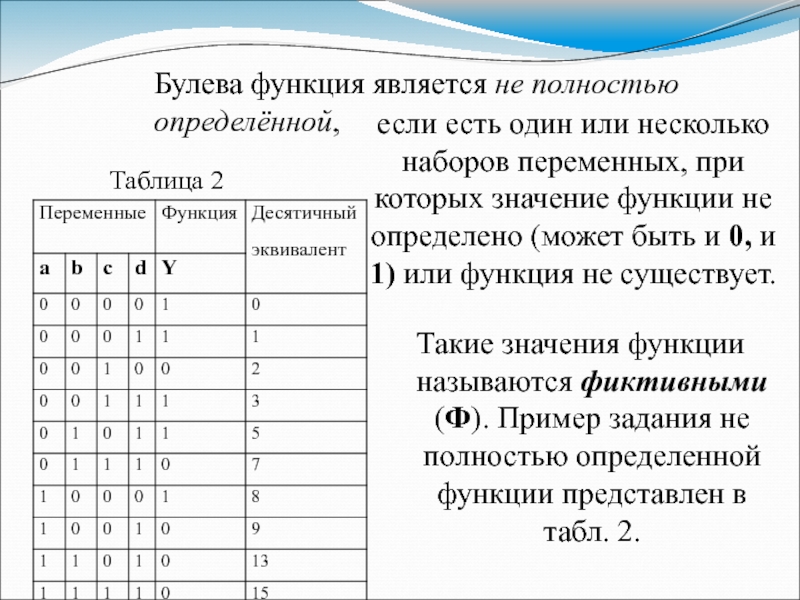
Слайд 23Такие значения функции называются фиктивными (Ф). Пример задания не полностью
определенной функции представлен в табл. 2.
если есть один или
несколько наборов переменных, при которых значение функции не определено (может быть и 0, и 1) или функция не существует.
Булева функция является не полностью определённой,
Таблица 2
Слайд 24Десятичное число, соответствующее двоичному набору логических переменных, называется десятичным эквивалентом.
Таким образом, булеву функцию можно представить с помощью десятичных эквивалентов:
Y1
= { 0,1,3,5,8} ; Y0 = {2,7,9,13,15}.
Оставшиеся наборы, не заданные таблицей истинности, по всей вероятности, будут фиктивными YФ = {4,6,10,11,12,14}.
Слайд 25По таблице истинности можно получить совершенные формы записи булевых функций.
Так, для записи в виде СДНФ нужно из таблицы выбрать
единичные наборы переменных, представить их в виде конституентов единицы и произвести их дизъюнкцию.
СДНФ: Y =abcd + abc d +ab c d +a bc d + abcd .
Слайд 26Для записи в форме СКНФ нужно выбрать из таблицы нулевые
наборы переменных, проинвертировать переменные в каждом из этих наборов, представить
в виде конституентов нуля и произвести их конъюнкцию.
СКНФ: Y=(a + b+c + d)(a+b +c +d)(a + b + c +d)(a +b + c +d)(a +b +c +d).
Аналогично можно составить СДНФ и СКНФ по десятичным эквивалентам, определяющим булеву функцию.
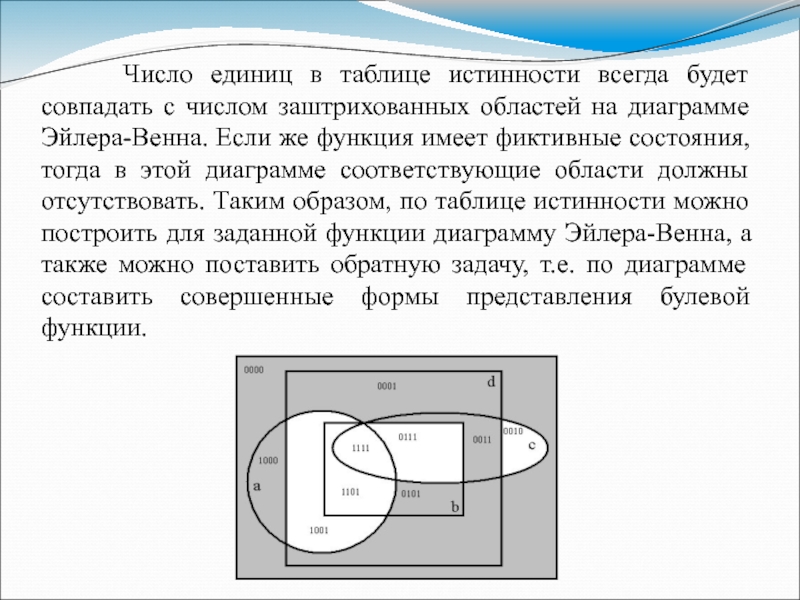
Слайд 27 Число единиц в таблице истинности всегда будет
совпадать с числом заштрихованных областей на диаграмме Эйлера-Венна. Если же
функция имеет фиктивные состояния, тогда в этой диаграмме соответствующие области должны отсутствовать. Таким образом, по таблице истинности можно построить для заданной функции диаграмму Эйлера-Венна, а также можно поставить обратную задачу, т.е. по диаграмме составить совершенные формы представления булевой функции.
Слайд 28Матрица Карно представляет собой специально организованные таблицы соответствия, обладающие тем
замечательным свойством, что любые две соседние клетки матрицы определяют «соседние»
наборы переменных, т.е. наборы, отличающиеся значением только одной переменной. Клетки, расположенные по краям матрицы, также являются соседними и обладают этим свойством. Это достигается благодаря кодированию столбцов и строк матрицы специальным циклическим кодом Грея.
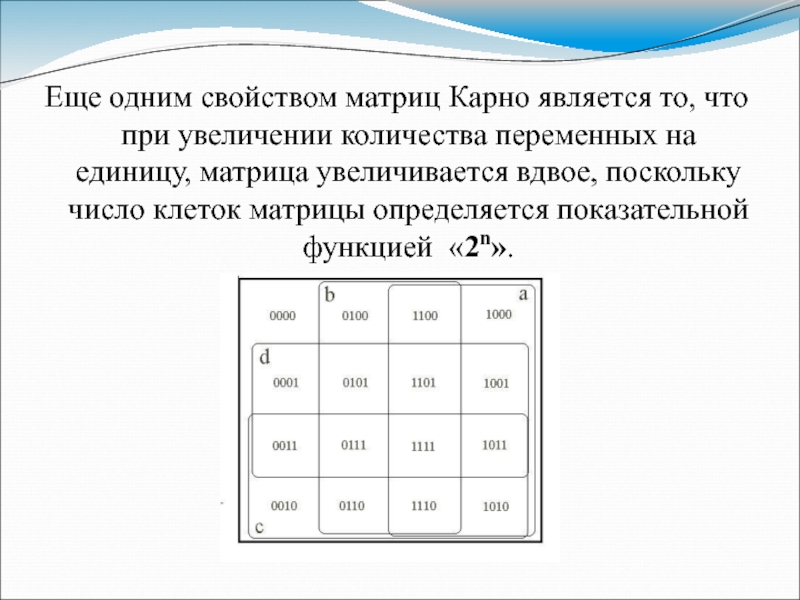
Слайд 29Еще одним свойством матриц Карно является то, что при увеличении
количества переменных на единицу, матрица увеличивается вдвое, поскольку число клеток
матрицы определяется показательной функцией «2n».
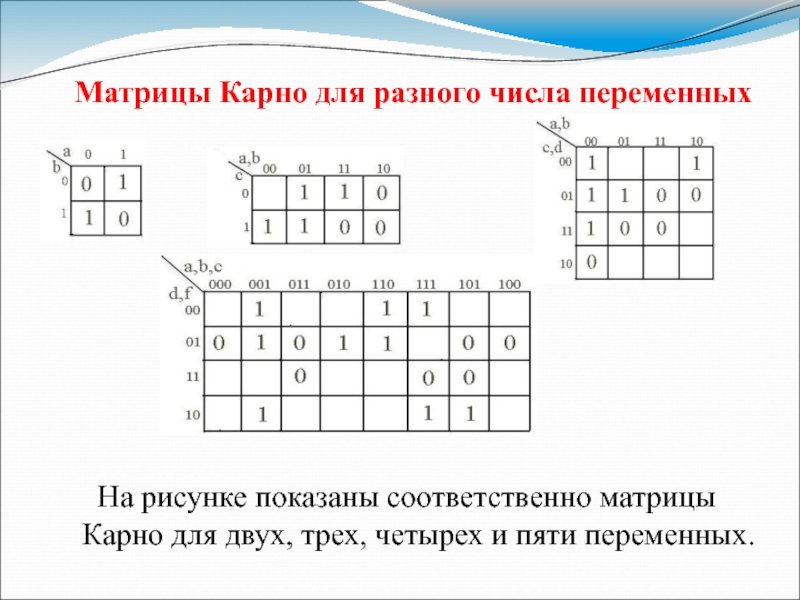
Слайд 30Матрицы Карно для разного числа переменных
На рисунке показаны соответственно
матрицы Карно для двух, трех, четырех и пяти переменных.













![Логика Буля.ppt 13. Разложения: f (a, b, c,..., x) = [a ∧ f 13. Разложения: f (a, b, c,..., x) = [a ∧ f (1,b,c,...,x)] ∨ [a∧ f (0,b,c,...,x)];f (a,](/img/thumbs/dbc80b7a69628b7083856efc9ffc8ad4-800x.jpg)



![Логика Буля.ppt Разложения функции на конституенты нуля:f(a,b,c)=[a + b + c + f(0,0,0) Разложения функции на конституенты нуля:f(a,b,c)=[a + b + c + f(0,0,0) ]·[a + b + c +](/img/thumbs/7bf1925de0fdea5801c5670aca461d88-800x.jpg)