Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ
Содержание
- 1. ЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ
- 2. ПОСТАНОВКА ЗАДАЧИ
- 3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК)
- 4. МЕТОД НАИМЕНЬШИХ КВАДРАТОВПараметры регрессии определяются из условия минимума остаточной суммы:
- 5. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ(3)
- 7. Слайд 7
- 8. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 9. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 10. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 11. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИПредставим последнее соотношение в эквивалентном виде:где
- 12. Было определение коэффициента корреляции:Выборочный коэффициент корреляции:
- 13. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИОбозначивполучимr - выборочный коэффициент корреляцииКоэффициент корреляции
- 14. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИС учетом (4) получаем:Эта формула обычно
- 15. Свойства выборочный коэффициента корреляции1. -1r1. Чем ближе
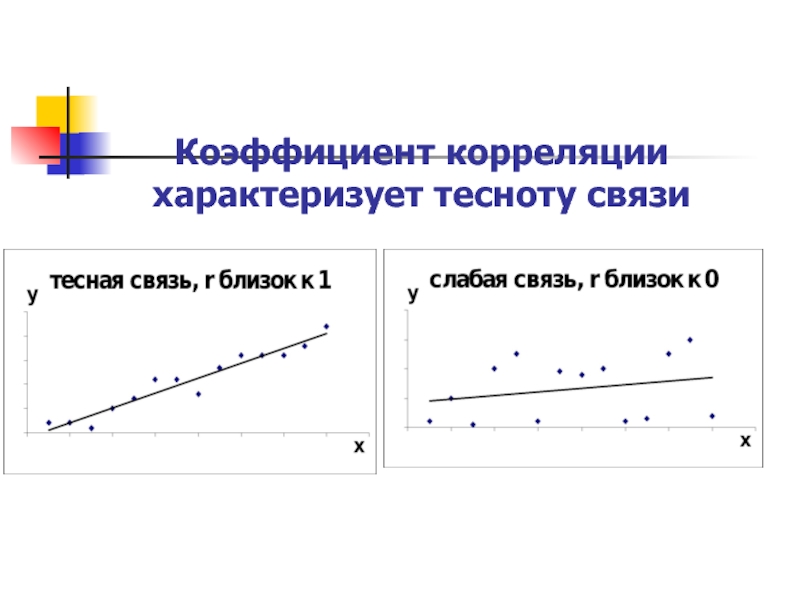
- 16. Коэффициент корреляции характеризует тесноту связи
- 17. Коэффициент корреляции характеризует тесноту связи
- 18. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯСогласно методу максимального правдоподобия (ММП),
- 19. Определения ТВ
- 20. По аналогии совместная плотность распределения двух случайныхз
- 21. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯПредположим, что: X -
- 22. В условиях этой моделиМЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 23. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯДля упрощения выкладок можно вместо
- 24. Свойства оценок максимального правдоподобияСостоятельностьАсимптотическая эффективностьАсимптотическая нормальность, для
- 25. Свойства оценок: несмещенностьМП-оценки могут иметь смещение!
- 26. Свойства оценок: состоятельностьдля состоятельной несмещенной оценки выполняется закон больших чисел
- 27. Свойства оценок: состоятельностьМожет использоваться для определения необходимого
- 28. Свойства оценок: эффективность
- 29. Несмещенность оценок параметров регрессии формула (3)Доказательство несмещенности параметра m:
- 30. Несмещенность оценок параметров регрессии
- 31. Несмещенность оценок параметров регрессии
- 32. Несмещенность оценок параметров регрессии
- 33. Теорема Гаусса-МарковаВ условиях классической нормальной регрессионной модели
- 34. ОЦЕНИВАНИЕ ДИСПЕРСИИ ВОЗМУЩЕНИЙЧисло неизвестных параметров (m, b)?для нормированных наблюдений
- 35. ИНТЕРВАЛЬНЫЕ ОЦЕНКИКакие оценки бывают, кроме интервальных?Что такое точечная оценка?Как характеризуется точность точечной оценки?
- 36. ИНТЕРВАЛЬНАЯ ОЦЕНКА ЗНАЧЕНИЙ ФУНКЦИИ РЕГРЕССИИ
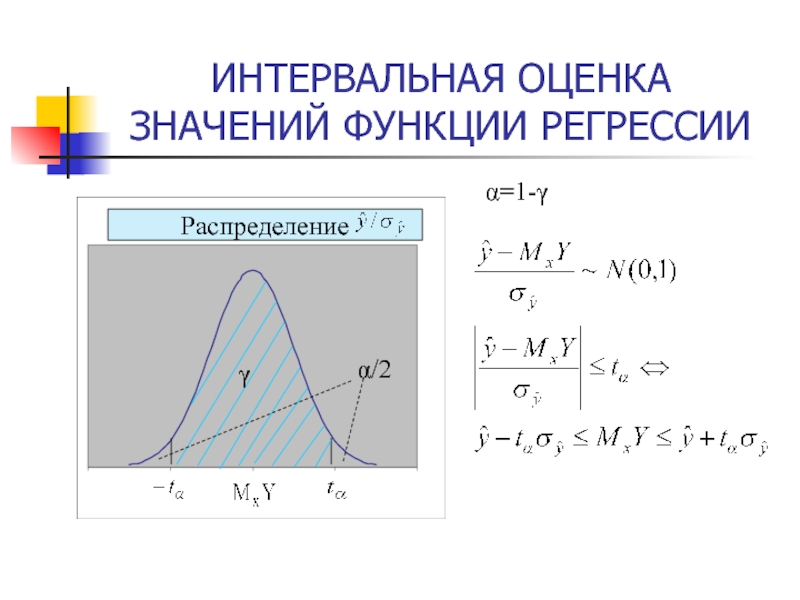
- 37. ИНТЕРВАЛЬНАЯ ОЦЕНКА ЗНАЧЕНИЙ ФУНКЦИИ РЕГРЕССИИ=1-γ
- 38. ИНТЕРВАЛЬНАЯ ОЦЕНКА ЗНАЧЕНИЙ ФУНКЦИИ РЕГРЕССИИ
- 39. ИНТЕРВАЛЬНАЯ ОЦЕНКА ЗНАЧЕНИЙ ФУНКЦИИ РЕГРЕССИИ
- 40. ИНТЕРВАЛЬНАЯ ОЦЕНКА ЗНАЧЕНИЙ ФУНКЦИИ РЕГРЕССИИ
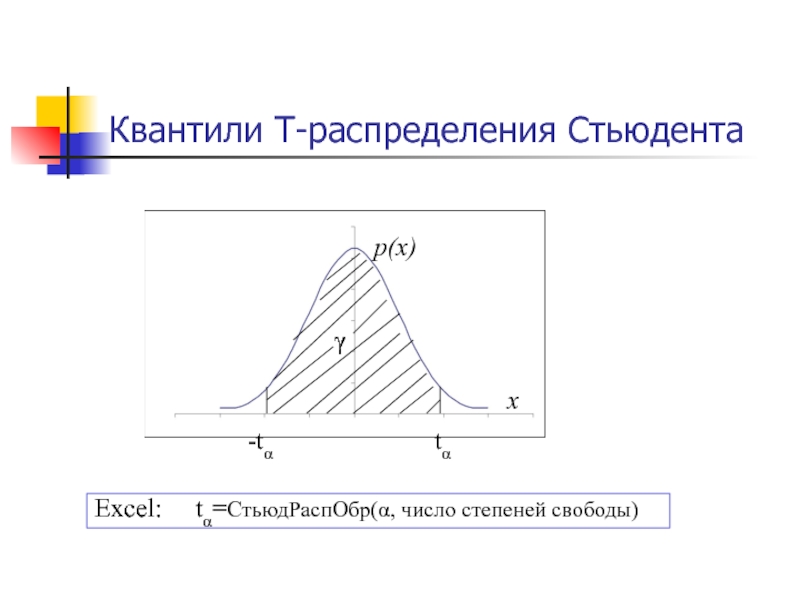
- 41. Квантили T-распределения СтьюдентаExcel: t=СтьюдРаспОбр(, число степеней свободы)
- 42. ИНТЕРВАЛЬНАЯ ОЦЕНКА ЗНАЧЕНИЙ ФУНКЦИИ РЕГРЕССИИВыводы из (10),
- 43. ИНТЕРВАЛЬНАЯ ОЦЕНКА ЗНАЧЕНИЙ ФУНКЦИИ РЕГРЕССИИ
- 44. Доверительный интервал для индивидуальных значений у
- 45. ИНТЕРВАЛЬНАЯ ОЦЕНКА ПАРАМЕТРА ФУНКЦИИ РЕГРЕССИИ()
- 46. ИНТЕРВАЛЬНАЯ ОЦЕНКА ПАРАМЕТРА ДИСПЕРСИИ ВОЗМУЩЕНИЙ
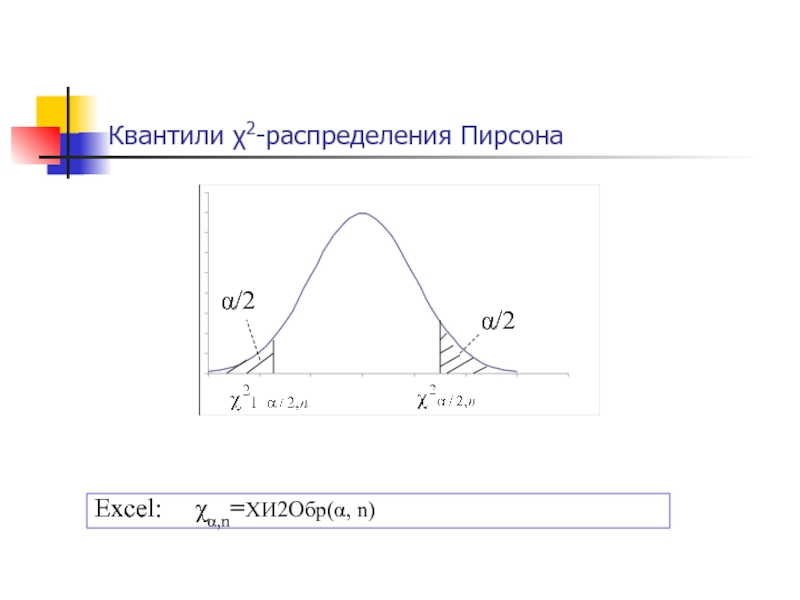
- 47. Квантили 2-распределения ПирсонаExcel: ,n=ХИ2Обр(, n)
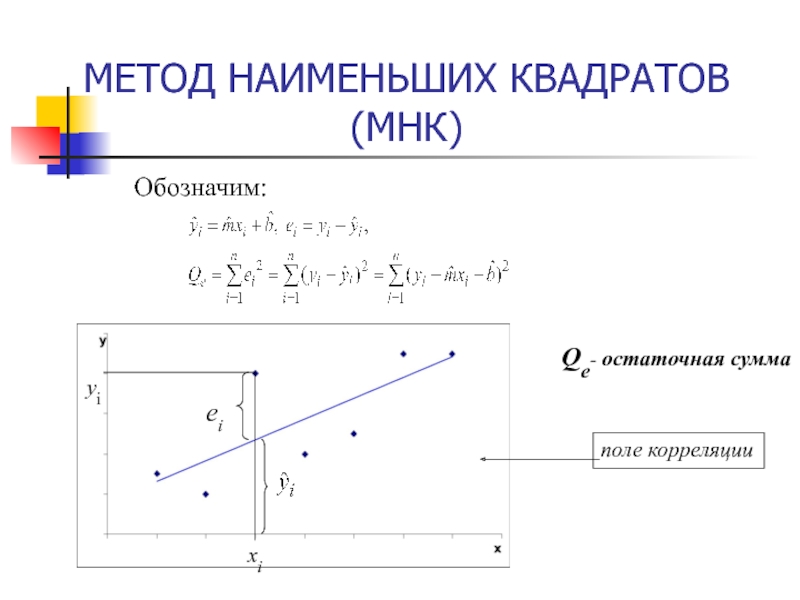
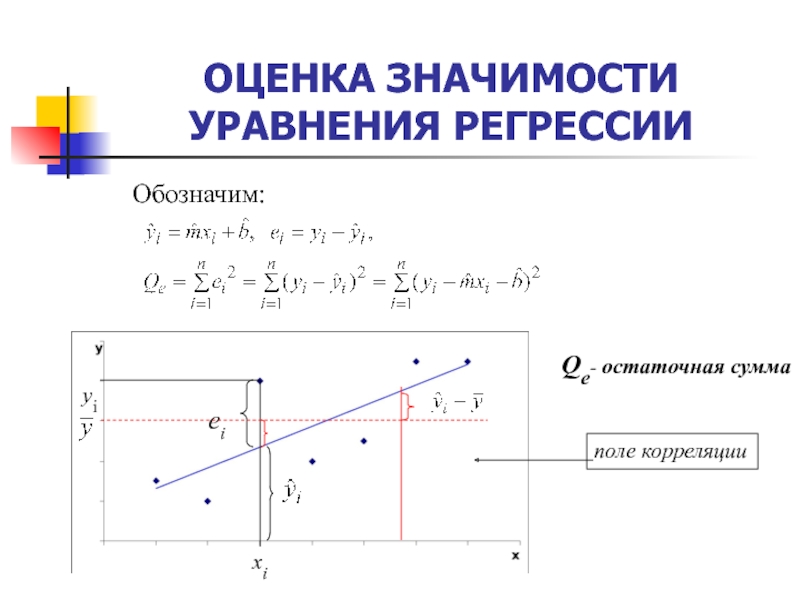
- 48. Обозначим:Qe- остаточная суммаОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
- 49. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
- 50. Чем меньше остаточная сумма Qe, тем выше
- 51. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИВ условиях теоремы Гаусса-Маркова
- 52. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИF показывает, в какой
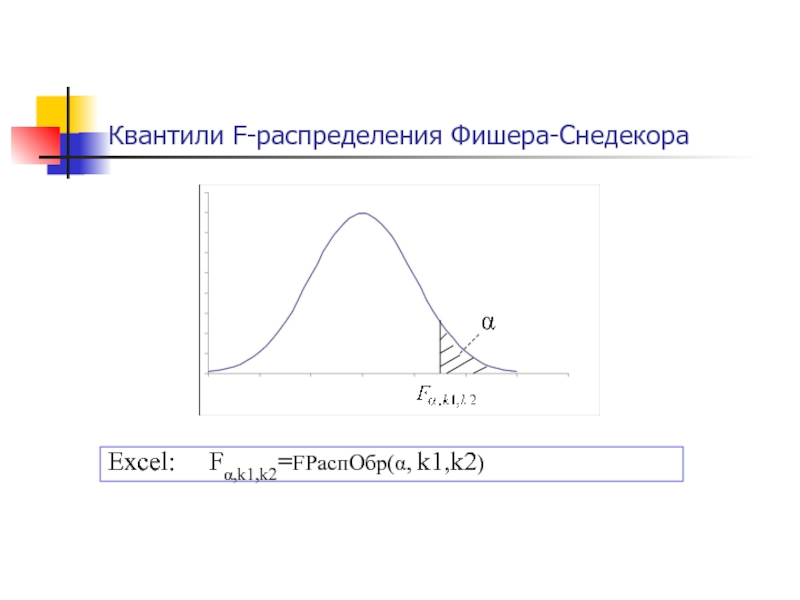
- 53. Квантили F-распределения Фишера-СнедекораExcel: F,k1,k2=FРаспОбр(, k1,k2)
- 54. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
- 55. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИКритерий (!) проверки гипотезы
- 56. ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИДругой способ оценки значимости
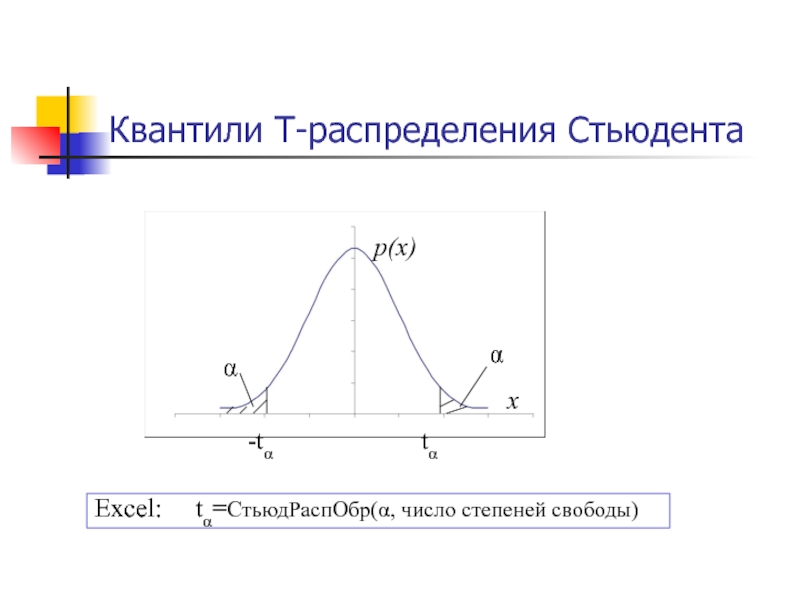
- 57. Квантили T-распределения СтьюдентаExcel: t=СтьюдРаспОбр(, число степеней свободы)
- 58. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Параметры регрессии определяются из условия минимума
остаточной суммы:
Слайд 13КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Обозначив
получим
r - выборочный
коэффициент корреляции
Коэффициент корреляции показывает, насколько величин sy
в среднем изменится y, если x изменится на sx.
Коэффициент корреляции
характеризует тесноту связи X и Y. Слайд 14КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
С учетом (4) получаем:
Эта формула обычно используется как
определение выборочного
коэффициента
корреляции
Для расчетов по таблице наблюдений применяется формула:
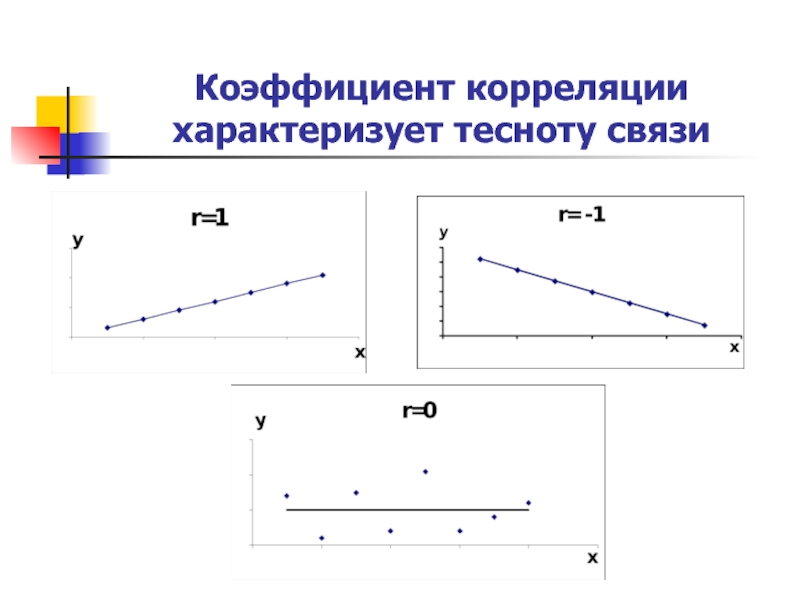
Слайд 15Свойства выборочный коэффициента корреляции
1. -1r1. Чем ближе r к 1,
тем теснее связь.
2. При r=1 корреляционная связь - линейная
(наблюдения располагаются на прямой)3. При r=0 связь отсутствует, линия регрессии параллельна оси ОХ.
Слайд 18МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
Согласно методу максимального правдоподобия (ММП), оценки параметров m
и b уравнения регрессии следует искать как точку максимума функции
правдоподобия, т. е. условной плотности вероятности распределения X и Y при заданных m и b :Для применения ММП необходимо иметь информацию
о распределении X и Y.
Слайд 20По аналогии совместная плотность распределения двух случайныхз величин Х и
По аналогии совместная плотность распределения двух случайных величин Х и
YСлайд 21МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
Предположим, что:
X - детерминированная величина;
1, …, n-
независимые нормальные одинаково распределенные случайные величины: i~N(0,2).
В этих предположениях соотношение
Y=mX+b+
называется
классической нормальной линейной регрессионной моделью
(Classical Normal Linear Regression model).Слайд 23МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
Для упрощения выкладок можно вместо функции (5) максимизировать
ее логарифм (т. к. логарифм - монотонная функция):
Из (6) следует,
что при известной дисперсии 2 для нахождения
оценок МП достаточно минимизировать Qe , и, следовательно,
МП-оценка совпадает с НК-оценкой.Слайд 24Свойства оценок максимального правдоподобия
Состоятельность
Асимптотическая эффективность
Асимптотическая нормальность, для линейной регрессии -
нормальность
???При нормальном распределении возмущений независимость оценок b и m
(для центрированных
наблюдений)Слайд 26Свойства оценок: состоятельность
для состоятельной
несмещенной
оценки выполняется
закон больших чисел
Слайд 27Свойства оценок: состоятельность
Может использоваться для определения необходимого числа
наблюдений, если
задано допустимое отклонение оценки от оцениваемого параметра и допустимая вероятность
отклонения.Другая формулировка закона больших чисел -
неравенство Чебышева:
Слайд 29Несмещенность оценок параметров регрессии
формула (3)
Доказательство несмещенности параметра m:
Слайд 33Теорема Гаусса-Маркова
В условиях классической нормальной регрессионной модели оценки (3) имеют
наименьшую дисперсию в классе всех линейных несмещенных оценок.
(3) -
самые эффективные оценки - Best Linear Unbiased Estimates (BLUE)
Слайд 34ОЦЕНИВАНИЕ ДИСПЕРСИИ ВОЗМУЩЕНИЙ
Число неизвестных параметров (m, b)
?для нормированных наблюдений
Слайд 35ИНТЕРВАЛЬНЫЕ ОЦЕНКИ
Какие оценки бывают, кроме интервальных?
Что такое точечная оценка?
Как характеризуется
точность точечной оценки?
Слайд 42ИНТЕРВАЛЬНАЯ ОЦЕНКА ЗНАЧЕНИЙ ФУНКЦИИ РЕГРЕССИИ
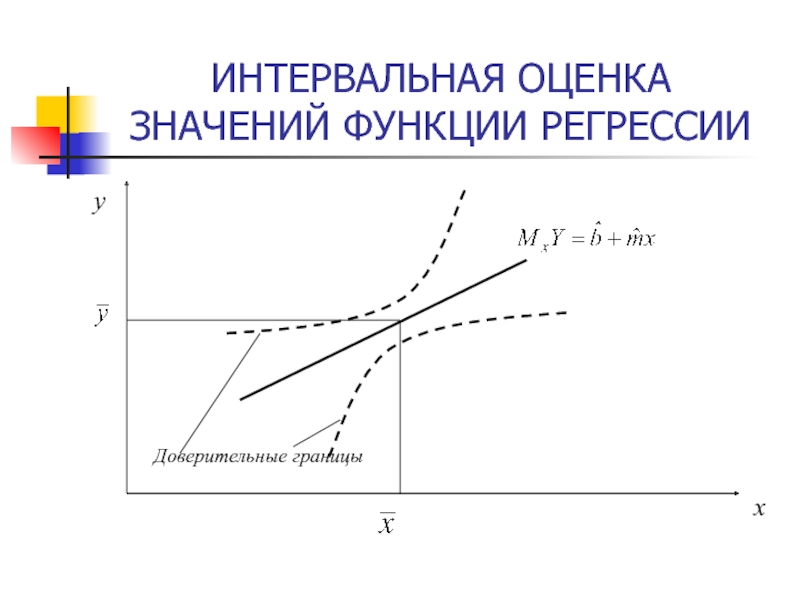
Выводы из (10), (11):
Точность оценивания
функции линейной регрессии зависит
от значения объясняющей переменной х.
Экстраполяция
с использованием линейной регрессии может
привести к существенным погрешностям. Слайд 50Чем меньше остаточная сумма Qe, тем выше качество модели.
Чем больше
регрессионная сумма QR, тем выше качество модели.
Чем больше отношение QR/Qe,
тем выше качество модели.Для перехода к стандартному распределению следует рассматривать не суммы, а средние квадраты.
ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
Слайд 52ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
F показывает, в какой мере регрессия лучше
оценивает значение
зависимой переменной по сравнению с ее средним значением
При
гипотеза
(предположение) о незначимости
регрессии отклоняется
с уровнем значимости .(!)
Неравенство (!) - правило (критерий) проверки гипотезы
о незначимости линейной регрессии,
F,k1,k2 - критическое (пороговое) значение F,
- вероятность отклонения гипотезы при условии, что она верна -
вероятность ошибки первого рода.
Слайд 55ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
Критерий (!) проверки гипотезы о незначимости регрессии
может
использовать значение R2 :
В случае парной регрессии: R2=r2
Слайд 56ОЦЕНКА ЗНАЧИМОСТИ УРАВНЕНИЯ РЕГРЕССИИ
Другой способ оценки значимости уравнения регрессии -
проверка гипотезы m=0
Правило проверки гипотезы о незначимости
уравнения регрессии: гипотеза
отклоняется при
t>t,n-2, (!!)
где - заданная вероятность ошибки 1 рода (уровень значимости)Для парной регрессии правила(!) и (!!) эквивалентны и F=t2
Для парной регрессии значимость уравнения регрессии эквивалентна значимости коэффициента регрессии