Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика ППИ. Лекция № 14
Содержание
- 1. Математика ППИ. Лекция № 14
- 2. ВОПРОСЫ ЛЕКЦИИ 1. Производная интеграла
- 3. ЛИТЕРАТУРА[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления.
- 4. УЧЕБНЫЙ ВОПРОС.Производная интеграла по верхнему пределу, формула Ньютона-Лейбница.
- 5. Производная интеграла по верхнему пределу, формула Ньютона-ЛейбницаПусть
- 6. Теорема. Если функция f(x) непрерывна на отрезке
- 7. Доказательство. Дадим аргументу x приращение Δx. Тогда приращение функции Ф(x) будет
- 8. К последнему интегралу применим теорему о среднем
- 9. Но так как Δx→0, то x+Δ x→x,
- 10. Формула Ньютона – Лейбница Теорема. Если функция
- 11. Слайд 11
- 12. Доказательство: Возьмем функцию Эта функция является первообразной
- 13. При x=a получим ,Так как
- 14. Пример 1. Вычислить интегралРешение.
- 15. Пример 2. Вычислить интегралРешение.
- 16. Пример 3. Вычислить интегралРешение.
- 17. УЧЕБНЫЙ ВОПРОС. Вычисление определённого интеграла заменой переменной и по частям.
- 18. Теорема. Пусть дан интеграл
- 19. Пример. Вычислить интегралРешение. Воспользуемся универсальной тригонометрической
- 20. 1) при вычислении определенного интеграла методом замены
- 21. Метод интегрирования по частям.Если функция u=u(x) и
- 22. Скачать презентанцию
ВОПРОСЫ ЛЕКЦИИ 1. Производная интеграла по верхнему пределу, формула Ньютона-Лейбница.2. Вычисление определённого интеграла заменой переменной и по частям.
Слайды и текст этой презентации
Слайд 2
ВОПРОСЫ ЛЕКЦИИ
1. Производная интеграла по верхнему пределу, формула Ньютона-Лейбница.
2. Вычисление
определённого интеграла заменой переменной и по частям.
Слайд 3ЛИТЕРАТУРА
[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва:
Интеграл-Пресс, 2004. с. 340-375;
[3] Б.П. Демидович, В.А. Кудрявцев. Краткий курс
высшей математики. Москва: Издательство АСТ, 2004.. с. 253-266;[14] Л.К. Потеряева, Г.А. Таратута. Курс высшей математики IV. Челябинск: Челябинский военный авиационный краснознамённый институт штурманов, 2002 г.с. 68-80.
Слайд 5Производная интеграла по верхнему пределу, формула Ньютона-Лейбница
Пусть y=f(x) – функция
непрерывна на отрезке [a,b]. Тогда она интегрируема на этом отрезке
и более того, она интегрируема на любом отрезке [a,x], где x∈[a,b] .Пусть нижний предел интегрирования a закреплен, а верхний предел интегрирования b – меняется.
Рассмотрим функцию
(1)
- интеграл с переменным верхним пределом.
Слайд 6Теорема. Если функция f(x) непрерывна на отрезке [a,b], тогда функция
непрерывна и имеет производную на отрезке [a,b]
Слайд 8К последнему интегралу применим теорему о среднем значении функции на
отрезке [x, x+∆x], получим:
то есть
Согласно определению производной
Слайд 9Но так как Δx→0, то x+Δ x→x, следовательно, и ξ→x.
Согласно
условию, подынтегральная функция f(t) непрерывна в точке x.
Поэтому
Таким образом,
что
и требовалось доказать.Слайд 10Формула Ньютона – Лейбница
Теорема. Если функция y=f(x) непрерывна на отрезке
[a,b] и F(x) –ее первообразная на [a,b], тогда:
или (2)
Слайд 12Доказательство: Возьмем функцию
Эта функция является первообразной для функции f(x)
на отрезке [a,b], а любые две первообразные для одной и
той же функции отличаются друг от друга постоянным слагаемым, то есть существует постоянная С такая, чтодля всех
Слайд 18Теорема. Пусть дан интеграл
где функция f(x) непрерывна
на отрезке [a;b]. Введем новую переменную t по формуле x=φ(t).
Если : 1) функция x=φ(t) и ее производная x′=φ′(t) непрерывны на отрезке [α;β] ;
2) φ(α)=a, φ(β)=b;
3) функция f(φ(t)) определенна и непрерывна на [α;β], тогда
Интегрирование заменой переменной.
Слайд 201) при вычислении определенного интеграла методом замены переменной (методом подстановки)
возвращаться к первоначальной переменной не требуется;
2) часто вместо подстановки x=φ(t)
, применяют подстановку t=g(x);3) необходимо менять пределы интегрирования при замене переменной.


![Математика ППИ. Лекция № 14 ЛИТЕРАТУРА[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, ЛИТЕРАТУРА[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004. с. 340-375;[3] Б.П. Демидович, В.А.](/img/thumbs/315798f7b63d0b2862df7793c5536617-800x.jpg)

![Математика ППИ. Лекция № 14 Производная интеграла по верхнему пределу, формула Ньютона-ЛейбницаПусть y=f(x) – функция непрерывна Производная интеграла по верхнему пределу, формула Ньютона-ЛейбницаПусть y=f(x) – функция непрерывна на отрезке [a,b]. Тогда она интегрируема](/img/thumbs/21c589fecd0ef2342d2fce7e510b5ea7-800x.jpg)
![Математика ППИ. Лекция № 14 Теорема. Если функция f(x) непрерывна на отрезке [a,b], тогда функция непрерывна Теорема. Если функция f(x) непрерывна на отрезке [a,b], тогда функция непрерывна и имеет производную на отрезке [a,b]](/img/thumbs/bd979016e2a3d31bac2b80ac2ca3a72f-800x.jpg)

![Математика ППИ. Лекция № 14 К последнему интегралу применим теорему о среднем значении функции на отрезке К последнему интегралу применим теорему о среднем значении функции на отрезке [x, x+∆x], получим: то естьСогласно определению](/img/thumbs/da610bd6f1c52e8f84b721798c49fa75-800x.jpg)

![Математика ППИ. Лекция № 14 Формула Ньютона – Лейбница Теорема. Если функция y=f(x) непрерывна на отрезке Формула Ньютона – Лейбница Теорема. Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) –ее первообразная на](/img/thumbs/8d1ef5c0cd93f961c91c7e2489e0a198-800x.jpg)
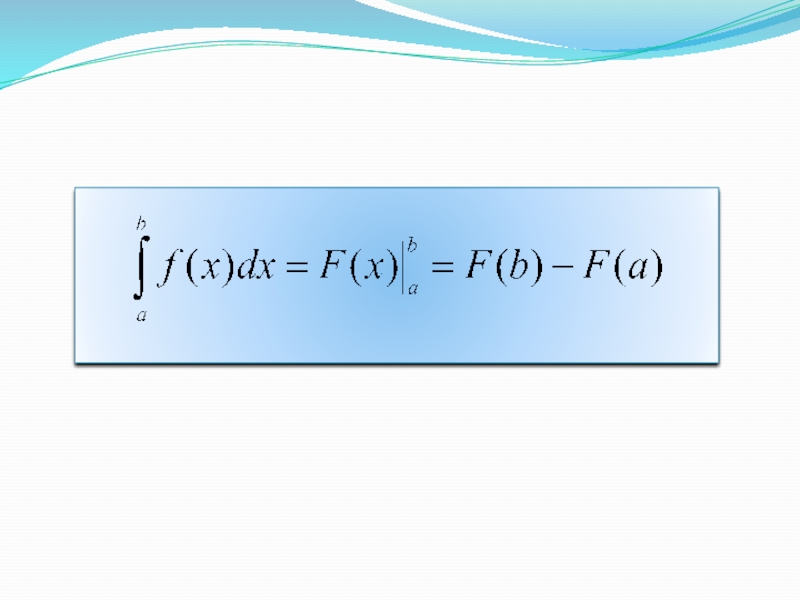
![Математика ППИ. Лекция № 14 Доказательство: Возьмем функцию Эта функция является первообразной для функции f(x) на Доказательство: Возьмем функцию Эта функция является первообразной для функции f(x) на отрезке [a,b], а любые две первообразные](/img/thumbs/576737b8140555a4977d9e1861ffcb7c-800x.jpg)








![Математика ППИ. Лекция № 14 Метод интегрирования по частям.Если функция u=u(x) и υ= υ (x) имеют Метод интегрирования по частям.Если функция u=u(x) и υ= υ (x) имеют непрерывные производные на отрезке [a;b], то](/img/thumbs/f4f72d5cb91a75aea5d731cb09a1d685-800x.jpg)