Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мир невозможных фигур
Содержание
- 1. Мир невозможных фигур
- 2. Выполнила: Политунова Татьяна8 класс.Научный руководительТреглазова
- 3. Мир невозможных фигуртема исследованияосновополагающий вопросВсегда ли невозможное - невозможно?
- 4. В природе существует много такого, что не
- 5. цель проектазадачи проектапроблемный вопросСуществуют ли в реальном
- 6. На протяжении всей истории люди сталкивались с
- 7. Оптические обманы в геометрииИллюзия восприятия глубины -
- 8. Самая простая фигура из Тьерри
- 9. Этот эффект использован в
- 10. Слайд 10
- 11. Невозможный треугольник Пенроуза (Удивительный треугольник – трибар) Данная
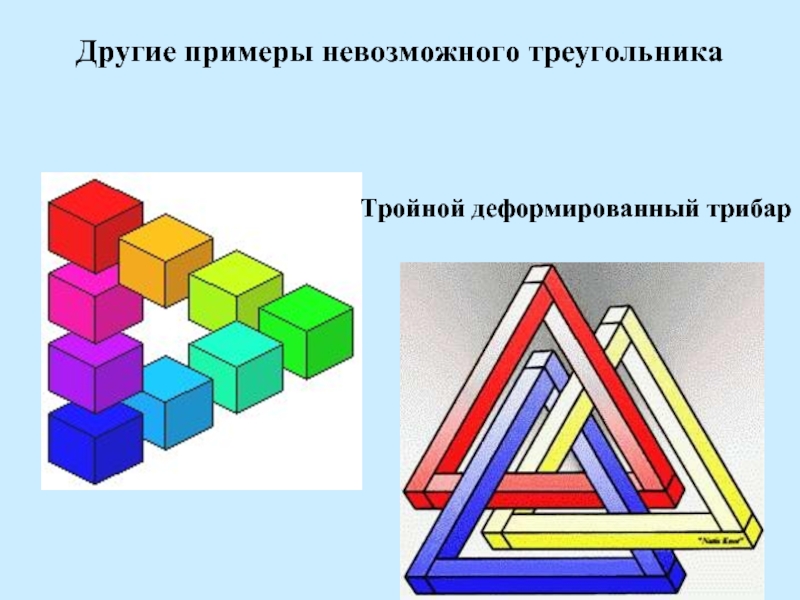
- 12. Другие примеры невозможного треугольникаТройной деформированный трибар
- 13. Крылатый трибарТройное доминоКубик со штифтамиУсеченный деформированный трибарПерекрещенный ромбУсеченный трибар
- 14. Среди всех невозможных фигур особое
- 15. Невозможные животныеПсихолог из Стенфорда Роджер Шепард (Roger Shepard) использовал идею трезубца для своей картины невозможного слона.
- 16. Многие художники использовали невозможный трезубец в своем
- 17. Невозможный куб Эшера Пример невозможного куба нидерландского
- 18. Американец Джерри Андрус увлекается созданием невозможных фигур
- 19. Так вот в чем секрет!
- 20. Вот еще один пример невозможной фигуры, созданной
- 21. В 1961 году М. К. Эшер (M. C. Escher)
- 22. Слайд 22
- 23. Намеренное использование невозможных
- 24. В начале XX века
- 25. Этот же художник создал
- 26. невозможные предметы Эшера «Восхождение и спуск». 1960
- 27. Этот предмет состоит из многих отдельных элементов,
- 28. О пользе имп-артаКак вы думаете, что в
- 29. Невозможные фигуры в реальном мире
- 30. Слайд 30
- 31. Эффект невозможности достигается за счет того, что
- 32. ЗаключениеТаким образом, можно сказать, что мир невозможных
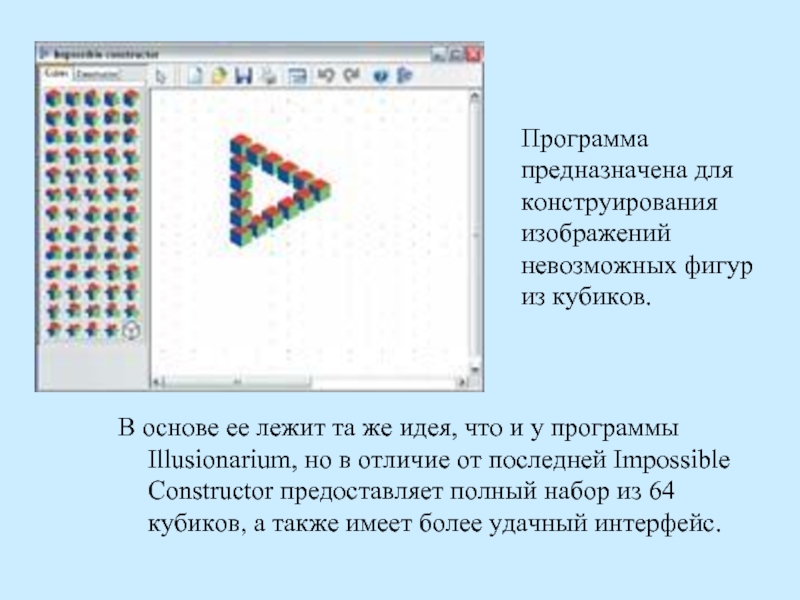
- 33. Для построения невозможных объектов используются программы —
- 34. Программа предназначена для конструирования изображений невозможных фигур
- 35. ЛитератураЖурнал «Наука и жизнь» 2005, №9Н. Лэнгдон, Ч. Снейт «С математикой в путь» М: «Педагогика», 1987http://www.geocities.jp/ikemath/3Drireki.htmhttp://www.impworld.narod.ru/.http://www.simplex.t.u-tokyo.ac.jp/~sugihara/hobby/hobbye.html
- 36. ЖЕЛАЮ УДАЧИ
- 37. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
Выполнила:
Политунова Татьяна
8 класс.
Научный руководитель
Треглазова Т. С.
Невозможное возможно
Слайд 3Мир невозможных фигур
тема исследования
основополагающий вопрос
Всегда ли невозможное - невозможно?
Слайд 4В природе существует много такого, что не может быть ни
достаточно глубоко понято, ни достаточно убедительно доказано, ни достаточно умело
и надежно использовано на практике без помощи вмешательства математики… Ф.БэконСлайд 5цель проекта
задачи проекта
проблемный вопрос
Существуют ли в реальном мире невозможные фигуры?
1.Выяснить,
как получаются несуществующие объекты.
2. Показать роль и значение невозможных фигур.
1.Изучить литературу по теме «Невозможные фигуры».2.Определить области существования невозможных фигур.
3.Составить каталог невозможных фигур.
4.Рассмотреть способы построения невозможных фигур.
Слайд 6
На протяжении всей истории люди сталкивались с оптическими иллюзиями того
или иного рода. Достаточно вспомнить мираж в пустыне, иллюзии создаваемые
светом и тенью, а также относительным движением. Широко известен следующий пример: луна, поднимающаяся из-за горизонта, кажется гораздо больше, чем высоко в небе. Все это – лишь несколько любопытных явлений, которые встречаются в природе. Когда эти явления, обманывающие зрение и ум, были впервые замечены, они стали волновать воображения людей.С давних времен оптические иллюзии использовались, чтобы усилить воздействие произведений искусства или улучшить внешний вид архитектурных творений. Древние греки прибегали к оптическим иллюзиям, чтобы довести до совершенства внешний вид своих великих храмов. В эпоху Средневековья смещенную перспективу иногда использовали в живописи. Позднее многие другие иллюзии использовались в графике. Среди них единственный в своем роде и относительно новый вид оптической иллюзии известен как "невозможные объекты".
Слайд 7Оптические обманы в геометрии
Иллюзия восприятия глубины - одна из самых
давнишних и известных оптических иллюзий. К этой группе принадлежит куб
Неккера (1832), а в 1895 году Арманд Тьерри (Armand Thiery) опубликовал статью об особом виде невозможных фигур. Объект состоит из пяти одинаковых ромбов с углами 60 и 120 градусов. На рисунке можно увидеть два куба, соединенные по одной поверхности. Если вести взгляд снизу вверх, отчетливо виден нижний куб с двумя стенками вверху, а если вести взгляд сверху вниз - верхний куб со стенками внизу.куб Неккера (1832)
Слайд 8 Самая простая фигура из Тьерри - подобных -
это, по-видимому, иллюзия "пирамида-проем", представляющая собой правильный ромб с линией
посередине. Нельзя сказать точно, что мы видим - пирамиду, возвышающуюся над поверхностью, или проем (впадину) на ней.Слайд 9 Этот эффект использован в графике "Лабиринт (План
пирамиды)" 2003 года. Картина получила диплом на международной математической конференции
и выставке в Будапеште в 2003 году "Ars(Dis)Symmetrica'03". В работе использованы сочетания иллюзии восприятия глубины и невозможных фигур.Слайд 10 "Невозможная
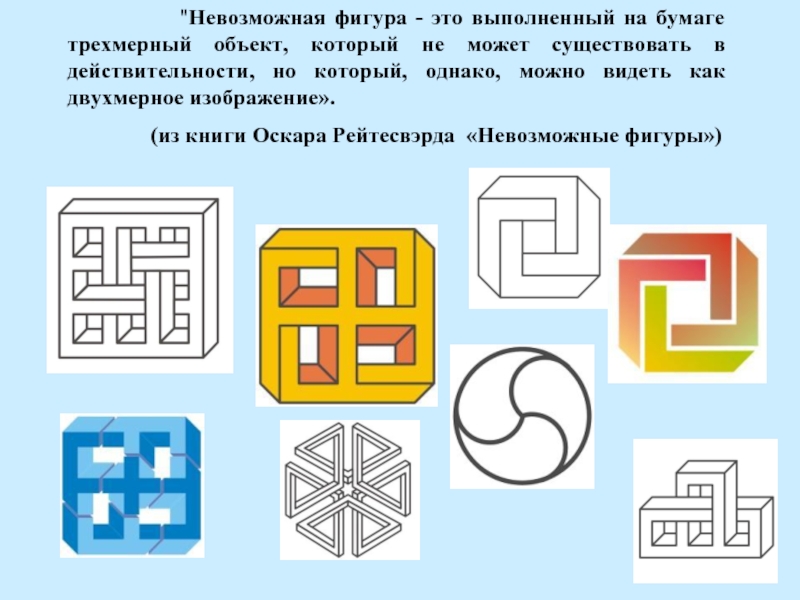
фигура - это выполненный на бумаге трехмерный объект, который не
может существовать в действительности, но который, однако, можно видеть как двухмерное изображение».(из книги Оскара Рейтесвэрда «Невозможные фигуры»)
Слайд 11Невозможный треугольник Пенроуза
(Удивительный треугольник – трибар)
Данная фигура придумана и нарисована
выдающимся учёным Роджером Пенроузом.
Роджер Пенроуз — выдающийся учёный современности,
активно работающий в различных областях математики, общей теории относительности и квантовой теории; 1958 г
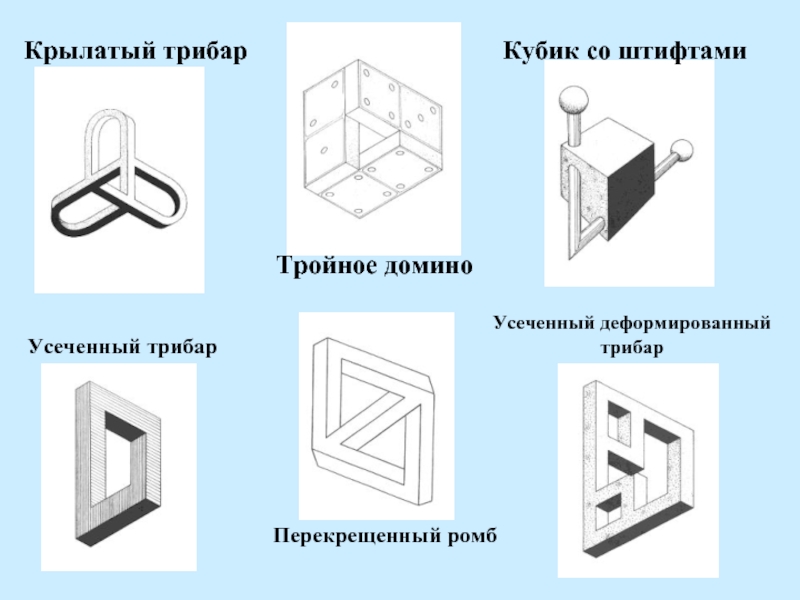
Слайд 13Крылатый трибар
Тройное домино
Кубик со штифтами
Усеченный деформированный
трибар
Перекрещенный ромб
Усеченный трибар
Слайд 14 Среди всех невозможных фигур особое место занимает невозможный
трезубец («чертова вилка»).
Если закрыть
рукой верхнюю часть трезубца, то мы увидим вполне реальную картину - три круглых зуба. Если закрыть нижнюю часть трезубца, то мы тоже увидим реальную картину - два прямоугольных зубца. Но, если рассматривать всю фигуру целиком, то получается что три круглых зубца постепенно превращаются в два прямоугольных. Таким образом, можно увидеть, что передний и задний планы данного рисунка конфликтуют. То есть, то что было изначально на переднем плане уходит назад, а задний план (средний зуб) вылезает вперед. Кроме смены переднего и заднего планов в данном рисунке присутствует еще один эффект – плоские грани верхней части трезубца становятся круглыми в нижней.
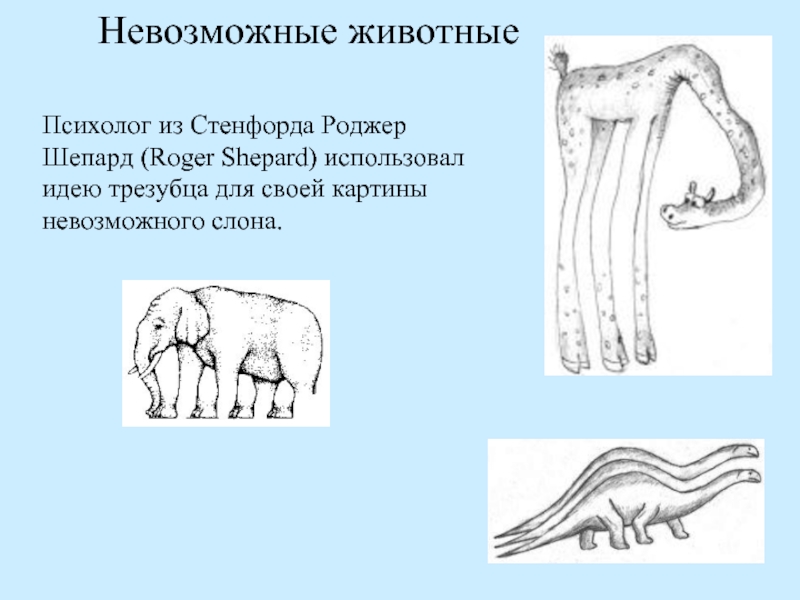
Слайд 15Невозможные животные
Психолог из Стенфорда Роджер Шепард (Roger Shepard) использовал идею трезубца
для своей картины невозможного слона.
Слайд 16 Многие художники использовали невозможный трезубец в своем творчестве. Японский художник
Шигео Фукуда (Shigeo Fukuda) в 1985 нарисовал невозможную колоннаду.
Слайд 17Невозможный куб Эшера
Пример невозможного куба нидерландского художника Эшера.
Мауриц Корнелис
Эшер - нидерландский художник-график. Известен прежде всего своими концептуальными литографиями,
гравюрами на дереве и металле, в которых он мастерски исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического восприятия сложных трёхмерных объектов.Слайд 18Американец Джерри Андрус увлекается созданием невозможных фигур в реальности. На
рисунке сфотографирована конструкция невозможного ящика.
Слайд 20Вот еще один пример невозможной фигуры, созданной американским фотографом
и
художником Уолтером Виком (Walter Wick). Невозможная собачья конура основана на
фигуре невозможного ящика, однако, конструкцияреальной фигуры значительно отличается от конструкции невозможного ящика Джерри Андруса
Слайд 21 В 1961 году М. К. Эшер (M. C. Escher) под впечатлением невозможного
трегольника, нарисованного Пенроузом (Пенроузы отослали копию статьи Эшеру) создал знаменитую
литографию "Водопад" ("Waterfall").«Водопад». 1961год.
Слайд 23 Намеренное использование невозможных объектов в дизайне
встречалось еще в древние времена до появления классической перспективы. Художники
пытались найти новые решения. Примером может служить датируемое XV веком изображение Благовещения на фреске собора Св. Марии в голландском городе Бреда. На картине изображен архангел Гавриил, приносящий Марии весть о ее будущем Сыне. Фреска обрамлена двумя арками, поддерживаемыми, в свою очередь тремя колоннами. Однако следует обратить внимание на среднюю колонну. В отличие от других, она исчезает на заднем плане за плитой. С практической точки зрения, художник использовал эту "невозможность" как особую технику, позволяющую избежать разделения сцены на две половины.
Мадонна с младенцем.
Слайд 24
В начале XX века художник Марсель Дюшамп
нарисовал рекламную картину «Apolinere enameled» (1916-1917), хранящуюся в Филадельфийском музее
искусства. В конструкции кровати на полотне можно разглядеть невозможные трех- и четырехугольники
«Apolinere enameled». 1916-1917 год.
Слайд 25 Этот же художник создал и прототип «невозможной
лестницы» (1950). Перед нами предстает лестница, ведущая, казалось бы, вверх
или вниз, но при этом человек, шагающий по ней, не поднимается и не опускается. Завершив свой визуальный маршрут, он окажется в начале пути. Если бы вам в самом деле пришлось пройти по этой лестнице, вы бы бесцельно поднимались и спускались по ней бесконечное число раз. Можно назвать это нескончаемым сизифовым трудом! С тех пор как Пенроузы опубликовали эту фигуру, она появлялась в печати чаще, чем какой-либо другой невозможный объект. "Бесконечную лестницу" можно встретить в книгах об играх, головоломках, иллюзиях, в учебниках по психологии и другим предметам.
Бесконечная лестница. 1950 год.