Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники и их основные свойства
Содержание
- 1. Многогранники и их основные свойства
- 2. Понятие о многогранниках.Тело, ограниченное плоскими многоугольниками, называются
- 3. ПризмаПризмой называется многогранник, у которого две грани
- 4. Отрезок, соединяющий две вершины призмы, не лежащие
- 5. Свойства призмы1. Боковые ребра призмы параллельны и
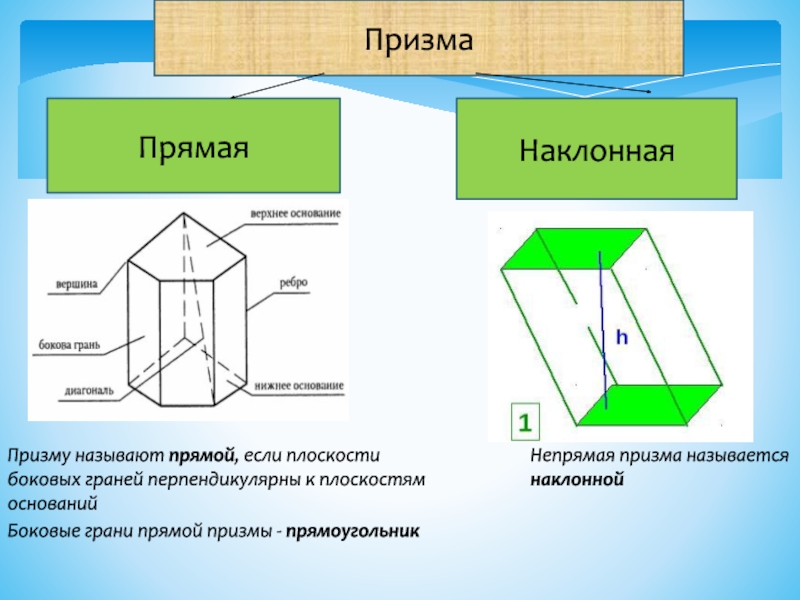
- 6. Призма Прямая Наклонная Призму называют прямой, если
- 7. Прямую призму называют правильной, если основанием её служит правильный многоугольник
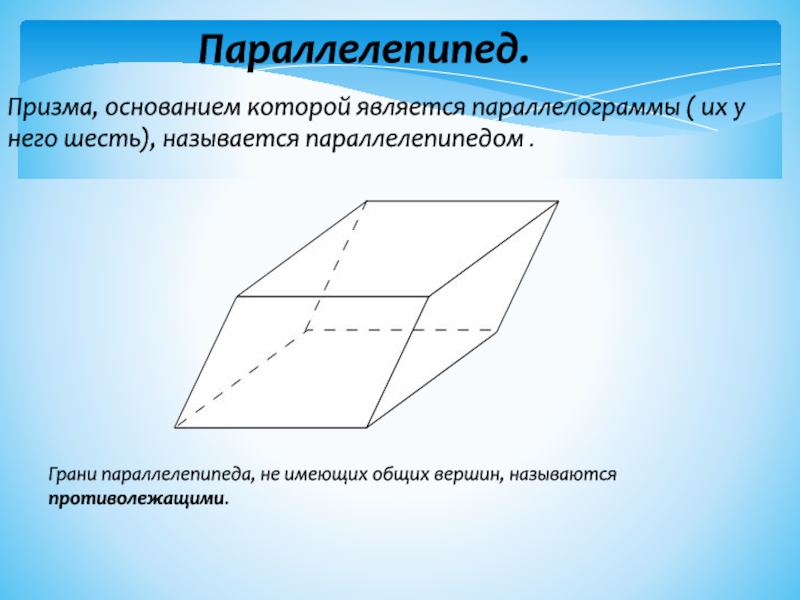
- 8. Параллелепипед.Призма, основанием которой является параллелограммы ( их у
- 9. Типы параллелепипедаПрямоугольный параллелепипед — объёмная фигура, у которой
- 10. КубПрямоугольный параллелепипед с равными измерениями называется кубом. Все
- 11. Площади призмыгде Росн- периметр основания,l-ребро призмы
- 12. Слайд 12
- 13. Решение задач по теме: «Призма и его виды»
- 14. Дано: А1А2А3А4-прямоугольникА1А4=5,А3А4=4,А/3А3=6Найти: А/2А4Решение:По свойству имеем: (А/2А4)2= (А1А4
- 15. 1. Найдите диагональ прямоугольного параллелепипеда, если его
- 16. Дано: А1А2А3А4-прямоугольникА1А4=5,А3А4=4,А/3А3=6Найти: Sбок, Sполн.Решение:
- 17. Дано: А1А2А3 –призма, А1А2=13, А1А3=14,
- 18. Слайд 18
- 19. 4.Найдите площади полной и боковой поверхности призмы
- 20. Скачать презентанцию
Понятие о многогранниках.Тело, ограниченное плоскими многоугольниками, называются многогранникомМногоугольники, ограничивающие многогранник, называются гранями, их стороны – ребрами, а вершины –вершинами многогранниками
Слайды и текст этой презентации
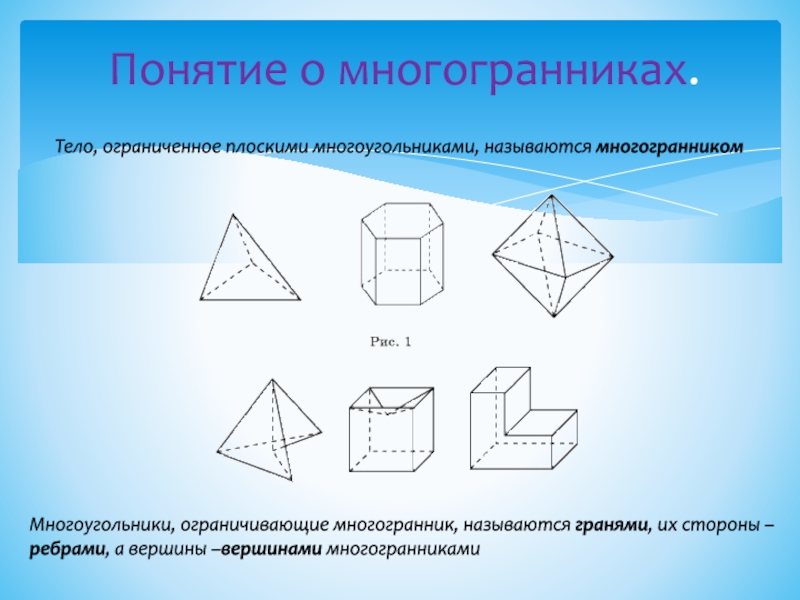
Слайд 2Понятие о многогранниках.
Тело, ограниченное плоскими многоугольниками, называются многогранником
Многоугольники, ограничивающие многогранник,
называются гранями, их стороны – ребрами, а вершины –вершинами многогранниками
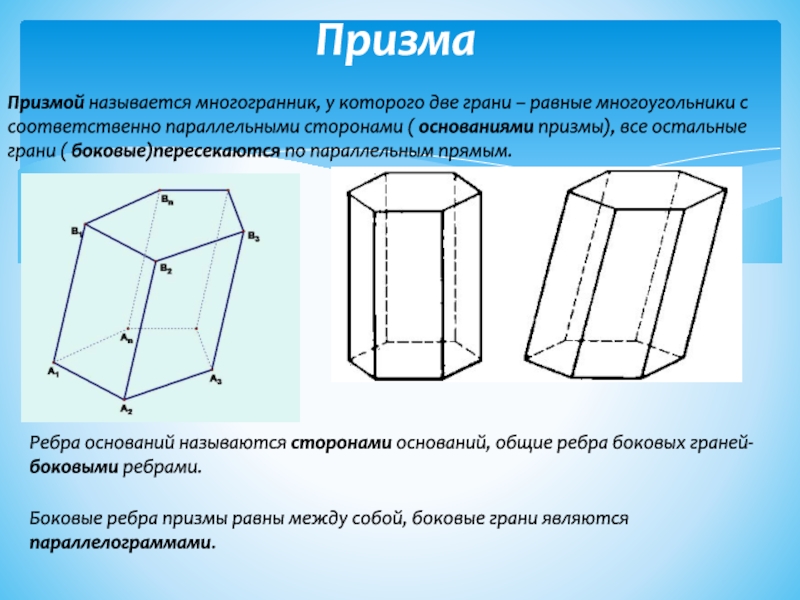
Слайд 3Призма
Призмой называется многогранник, у которого две грани – равные многоугольники
с соответственно параллельными сторонами ( основаниями призмы), все остальные грани
( боковые)пересекаются по параллельным прямым.Ребра оснований называются сторонами оснований, общие ребра боковых граней- боковыми ребрами.
Боковые ребра призмы равны между собой, боковые грани являются параллелограммами.
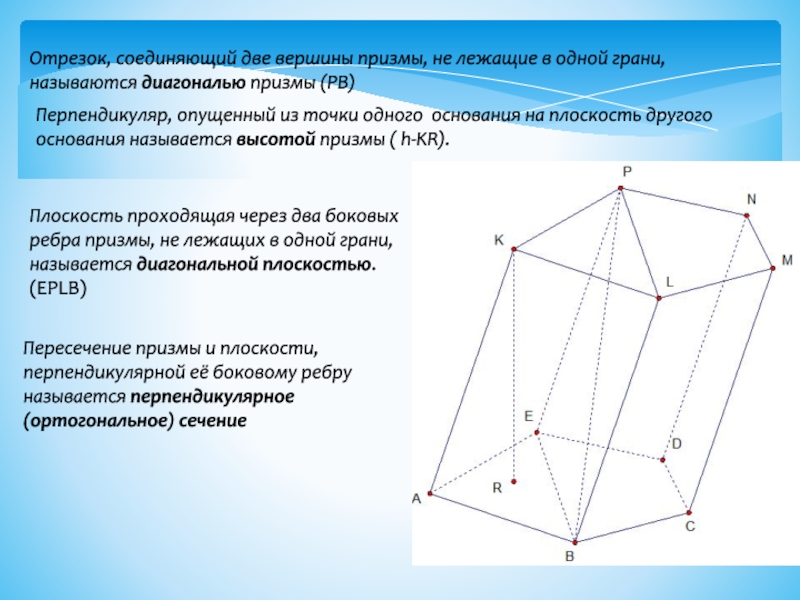
Слайд 4Отрезок, соединяющий две вершины призмы, не лежащие в одной грани,
называются диагональю призмы (PB)
Перпендикуляр, опущенный из точки одного основания на
плоскость другого основания называется высотой призмы ( h-KR).Плоскость проходящая через два боковых ребра призмы, не лежащих в одной грани, называется диагональной плоскостью. (EPLB)
Пересечение призмы и плоскости, перпендикулярной её боковому ребру называется перпендикулярное (ортогональное) сечение
Слайд 5Свойства призмы
1. Боковые ребра призмы параллельны и равны.
2. Перпендикулярное сечение
перпендикулярно ко всем боковым рёбрам призмы.
3. Углы перпендикулярного сечения — это
линейные углы двугранных углов при соответствующих боковых рёбрах.4. Перпендикулярное сечение перпендикулярно ко всем боковым граням
Слайд 6Призма
Прямая
Наклонная
Призму называют прямой, если плоскости боковых граней
перпендикулярны к плоскостям оснований
Непрямая призма называется наклонной
Боковые грани прямой призмы
- прямоугольник
Слайд 8 Параллелепипед.
Призма, основанием которой является параллелограммы ( их у него шесть), называется параллелепипедом
.
Грани параллелепипеда, не имеющих общих вершин, называются противолежащими.
Слайд 9Типы параллелепипеда
Прямоугольный параллелепипед — объёмная фигура, у которой шесть граней, и
каждая из них является прямоугольником.
Квадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов трех его измерений
Слайд 10Куб
Прямоугольный параллелепипед с равными измерениями называется кубом. Все шесть граней куба —
равные квадраты
Квадрат диагонали куба равен утроенному произведению квадратов его ребер
Слайд 14Дано: А1А2А3А4-прямоугольник
А1А4=5,
А3А4=4,
А/3А3=6
Найти: А/2А4
Решение:
По свойству имеем:
(А/2А4)2= (А1А4 )2+ (А3А4)2 +
(А/3А3)2
(А/2А4)2= (5 )2+ (4)2 + (6)2
(А/2А4)2= 25+ 16+ 36
(А/2А4)2= 77
Слайд 151. Найдите диагональ прямоугольного параллелепипеда, если его измерения равны: 1,1,2
2.
Найдите диагональ прямоугольного параллелепипеда, если его измерения равны: 8,9,12
3. Найдите
диагональ прямоугольного параллелепипеда, если его измерения равны: 12,16,21
Слайд 194.Найдите площади полной и боковой поверхности призмы , если дана
правильная треугольная призма, с основанием 10 и боковым ребром 15.
5.Найдите
площади полной и боковой поверхности призмы , если дана правильная четырехугольная призма, с основанием 12 и высотой 8
