Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели оптимального планирования Урок 51
Содержание
- 1. Модели оптимального планирования Урок 51
- 2. Домашнее задание §20 (с.126–131).Вопросы 1–3 – устно.
- 3. деятельность отдельного предприятия,деятельность отрасли промышленности или сельского хозяйства,деятельность региона, деятельность государства.Объекты планирования
- 4. Постановка задачи планированияИмеются некоторые плановые показатели: х,
- 5. Оптимальное планированиеОптимальное планирование заключается в определении значений плановых показателейс учетом ограниченности ресурсовпри условии достижения стратегической цели.
- 6. Ограниченность ресурсовУсловия ограниченности ресурсов математически представляются в виде системы неравенств и (или) равенств.
- 7. Стратегическая цельРешение задачи оптимального планирования сводится к
- 8. ПримерОбъект: детский садПлановые показатели: 1) число детей,
- 9. ЗадачаКондитерский цех готовит пирожки и пирожные. Ограниченность
- 10. Математическая модель задачиПлановые показатели:x – дневной план
- 11. В итоге получаем систему неравенств:
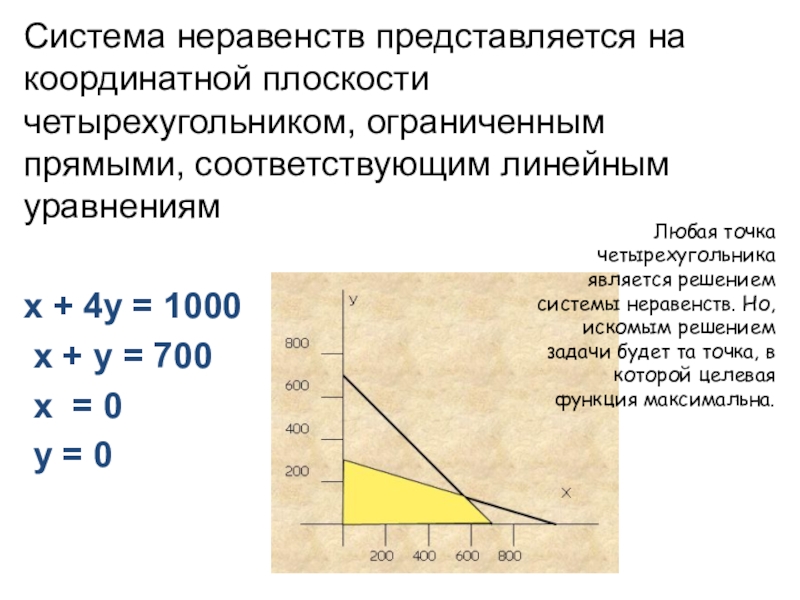
- 12. Система неравенств представляется на координатной плоскости четырехугольником,
- 13. Формализация стратегической цели: получение максимальной выручкиПусть цена
- 14. Таким образом, получение оптимального плана свелось к
- 15. Математическое программированиеМатематическая дисциплина, которая посвящена решению задач
- 16. Методы линейного программирования встроены в MS Excel в виде надстройки «Поиск решения».Средство Excel «Поиск решения»
- 17. Работаем за компьютером
- 18. Скачать презентанцию
Домашнее задание §20 (с.126–131).Вопросы 1–3 – устно.
Слайды и текст этой презентации
Слайд 3деятельность отдельного предприятия,
деятельность отрасли промышленности или сельского хозяйства,
деятельность региона,
деятельность
государства.
Слайд 4Постановка задачи планирования
Имеются некоторые плановые показатели: х, у и др.
Имеются
некоторые ресурсы: R1, R2 и др., за счет которых эти
плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены.Имеется определенная стратегическая цель, зависящая от значений х, у и других плановых показателей, на которую следует ориентировать планирование.
Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.
Слайд 5Оптимальное планирование
Оптимальное планирование заключается
в определении значений плановых показателей
с учетом ограниченности
ресурсов
при условии достижения стратегической цели.
Слайд 6Ограниченность ресурсов
Условия ограниченности ресурсов математически представляются в виде системы неравенств
и (или) равенств.
Слайд 7Стратегическая цель
Решение задачи оптимального планирования сводится к построению целевой функции
и назначению определенных условий для ее величины: чаще всего максимума
или минимума.
Слайд 8Пример
Объект: детский сад
Плановые показатели:
1) число детей, 2) число воспитателей
Основные
ресурсы деятельности детского сада:
1) размер финансирования, 2) площадь помещения
Стратегические цели:
сохранение и укрепление здоровья детей (минимизация заболеваемости воспитанников детского сада)
Слайд 9Задача
Кондитерский цех готовит пирожки и пирожные. Ограниченность емкости склада –
за день можно приготовить не более 700 изделий. Рабочий день
– 8 часов. Если выпускать только пирожные, за день можно произвести не более 250 штук, пирожков можно произвести 1000 штук (без пирожных). Стоимость пирожного вдвое выше, чем стоимость пирожка. Требуется составить дневной план производства, обеспечивающий наибольшую выручку.
Слайд 10Математическая модель задачи
Плановые показатели:
x – дневной план выпуска пирожков;
y -
дневной план выпуска пирожных.
Ресурсы производства:
Длительность рабочего дня – 8 часов,
Вместимость
склада – 700 мест.Время изготовления пирожного в 4 раза больше времени изготовления пирожка.
Строим модель
Длительность рабочего дня (8 часов) выразим в минутах – 8*60=480 мин.
Вычислим t (время изготовления одного пирожка):
t = 480/1000 = 0,48 мин.
Суммарное время на изготовление х пирожков и у пирожных равно
tх + 4ty = (х + 4у)t.
Получим:
Ограничение на время (х + 4у)*0,48 < 480 или х + 4у < 1000 .
Ограничение на общее число изделий х + у < 700 .
Добавим условия положительности значений величин х и у.
Слайд 12Система неравенств представляется на координатной плоскости четырехугольником, ограниченным прямыми, соответствующим
линейным уравнениям
х + 4у = 1000
х + у
= 700х = 0
у = 0
Любая точка четырехугольника является решением системы неравенств. Но, искомым решением задачи будет та точка, в которой целевая функция максимальна.
Слайд 13Формализация стратегической цели: получение максимальной выручки
Пусть цена одного пирожка –
r рублей,
тогда цена пирожного – 2r рублей, а стоимость всей
произведенной за день продукции равна
rx + 2ry = r(x + 2y).Запишем полученное выражение как функцию f(x,y) = r(x + 2y).
Она называется целевой функцией. Так как r – константа, в качестве целевой функции можно принять
f(x,y) = (x + 2y).
Слайд 14Таким образом, получение оптимального плана свелось к решению следующей математической
задачи:
Найти значения плановых показателей х и у, удовлетворяющих системе неравенств
при которых целевая функция
f(x,y) = (x + 2y)
принимает максимальное значение.
х + 4у < 1000
х + у < 700
х ≥ 0
у ≥ 0
Слайд 15Математическое программирование
Математическая дисциплина, которая посвящена решению задач оптимального планирования, называется
математическим программированием.
Если целевая функция f(x, у) линейная, то решение такой
задачи называется линейным программированием.
Слайд 16Методы линейного программирования встроены в MS Excel в виде надстройки
«Поиск решения».
Средство Excel «Поиск решения»
