Слайд 2Лютфи Аскер Заде (англ. Lotfi Asker Zadeh, р. 4 февраля
1921) — математик, основатель теории нечётких множеств и нечёткой логики.
Родился в Баку, с 1932 года жил в Иране, учился в Alborz High School и Тегеранском университете; с 1944 в Соединенных Штатах; с 1959 работает в Калифорнийском университете (Беркли).
В 1965 опубликовал основополагающую работу по теории нечётких множеств, в которой изложил математический аппарат теории нечётких множеств; в 1973 предложил теорию нечёткой логики; позднее — теорию мягких вычислений (soft computing); а также — теорию вербальных вычислений и представлений (computing with words and perceptions).
Слайд 3Основные понятия теории нечетких множеств
Пусть Е есть
множество, счетное или нет, и x — элемент Е. Тогда
нечетким подмножеством А множества Е называется множество упорядоченных пар
{(x| A(x))}, x Е,
где A(x) — степень принадлежности x в А. Таким образом, если A(x) принимает свои значения во множестве М значений функции принадлежности или, короче, во множестве принадлежностей, то можно сказать, что x принимает значение в М посредством функции A(x). Эта функция также называется функцией принадлежности.
(Определение Л. Заде)
Слайд 4Определение А. Кофмана
Пусть Е есть множество, счетное
или нет, и x — элемент Е. Тогда нечеткое подмножество
А множества Е определяется как множество упорядоченных пар
{(x| A(x))}, x Е,
где A(x) — характеристическая функция принадлежности x в А, принимающая свои значения во вполне упорядоченном множестве М, которая указывает степень или уровень принадлежности элемента x подмножеству А. Множество М будет называться множеством принадлежностей.
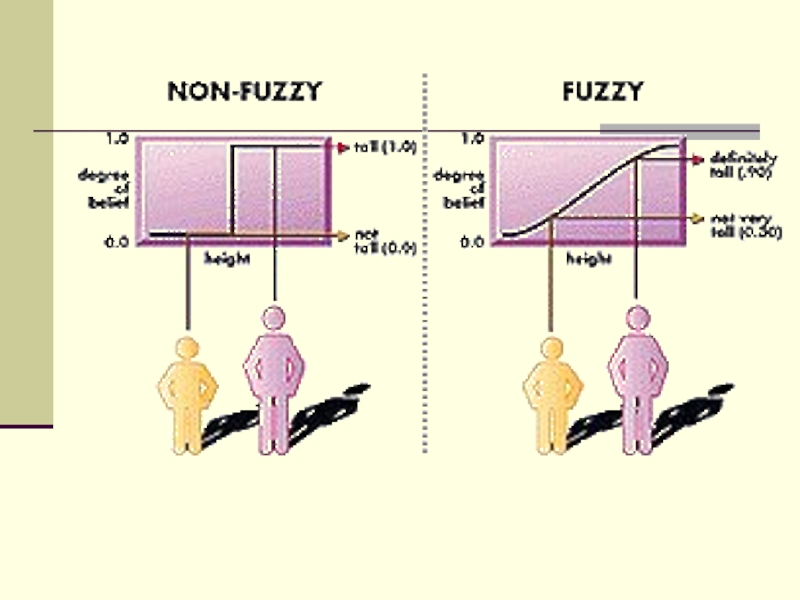
Слайд 6Что означает степень принадлежности?
В работе Заде «Fuzzy sets» предполагается, что
функция принадлежности — это некоторое «невероятностное субъективное измерение неточности», и
что она отлична от плотности вероятности и от функции распределения вероятности.
В работе Заде «Понятие лингвистической переменной и его применение к принятию приближенных решений» под значением функции принадлежности µА(u) нечеткого множества А для любого u U понимается вероятность того, что ЛПР отнесет элемент u к множеству А. В случае, когда А – некоторое понятие естественного языка, а U – множество объектов, обозначаемых этим понятием А, µА(u) – есть вероятность того, что лицо, принимающее решение, использует А в качестве имени объекта.
Такая интерпретация функции принадлежности называется вероятностной и не исключает существование других интерпретаций. Однако
− элемент u, как следует из определения, уже предъявлен ЛПР, а последний и решает задачу отнесения элемента к нечеткому множеству А;
− в приведенной интерпретации µА(u) не является ни функцией распределения вероятности, ни плотностью распределения вероятности

Слайд 7Что означает степень принадлежности?
степень соответствия понятию А,
вероятность,
возможность,
полезность,
истинность,
правдоподобность,
значение функции
и др.
Слайд 8Методы построения функции принадлежности
частотный (вероятностная интерпретация)
метод парных соотношений: есть n
экспертов, каждый определяет парные соотношения, из них определяется экспертная оценка
степени принадлежности, оценки усредняются по экспертам
на основе стандартного набора графиков, выбранный график ЛПР корректирует
Слайд 9Наиболее распространенные параметрические функции принадлежности
Треугольные
m(x) = 0, при x
m(x) = (x – a)/(b – a), при a < x
(c – x)/(c – b), при b < x <=c;
m(x) = 0, при с < x.
Трапециевидные
m(x) = 0, при x
m(x) = (x – a)/(b – a), при a < x <=b;
m(x)= 1, при b < x <=c;
m(x) = (d – x)/(d – c), при c < x <=d;
m(x) = 0, при d < x.
Слайд 10Гауссовские функции принадлежности задаются двумя параметрами (c,s):
m(x) = exp(
0.5(x c)^2/s^2).
Колоколообразные функции принадлежности задаются параметрами (a,b,c):
m(x)
= 1/(1+((x c)/a)^(2b))
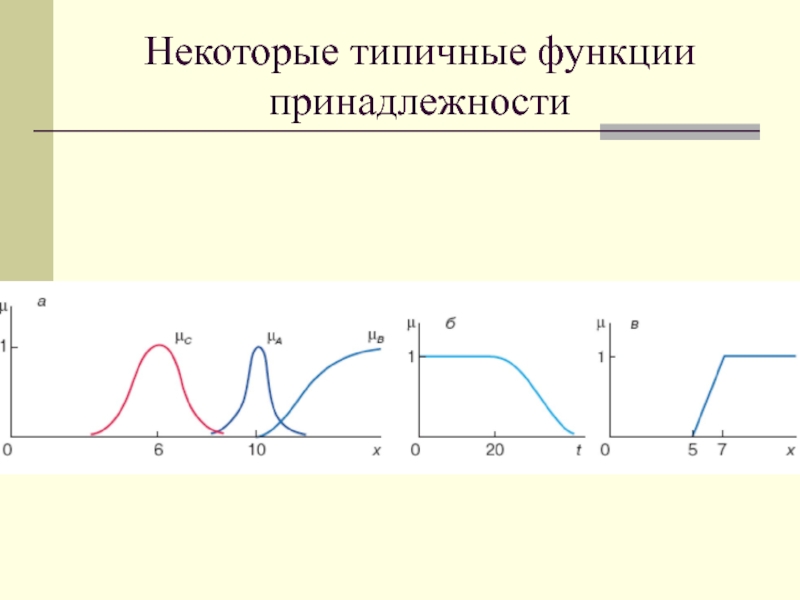
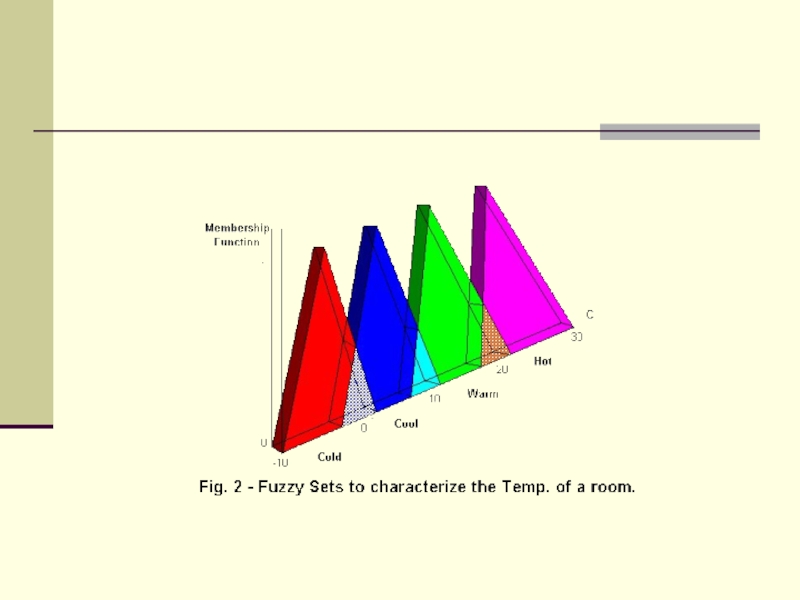
Слайд 11Некоторые типичные функции принадлежности
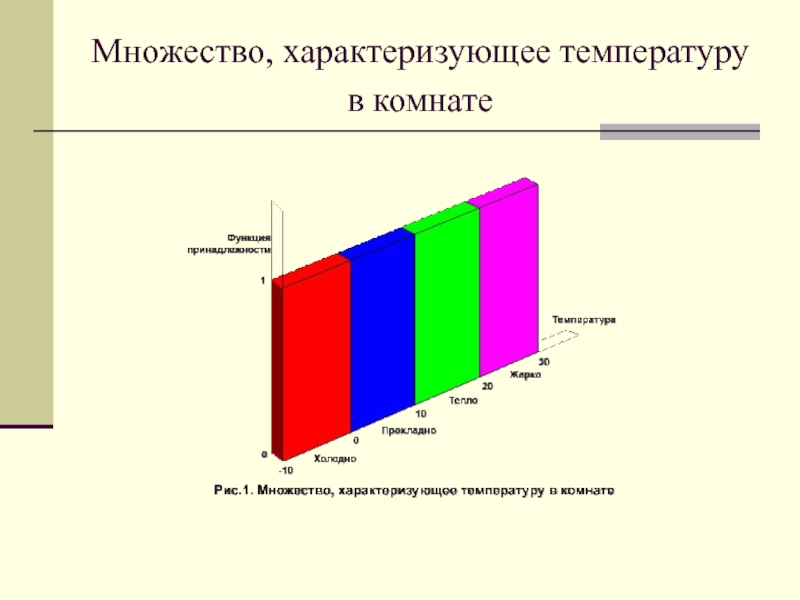
Слайд 12Множество, характеризующее температуру в комнате
Слайд 15Нечеткое множество А называется пустым, если A(x) = 0, x Е
Носителем нечеткого
множества А называется обычное подмножество таких точек Е, для
которых величина A(x) положительна. Носитель обозначается S(A) или Supp A: S(A) = {x| x Е, A(x) > 0}
Высотой h(A) нечеткого множества А называется величина h(A) = sup A(x) по всем x Е
Нечеткое множество А называется нормальным, если его высота равна единице. В противном случае нечеткое множество А субнормально.
Элементы множества Е, для которых степень принадлежности A(x) = 0.5 называются точками перехода нечеткого множества
Слайд 16Логические операции над нечеткими множествами
Операция включения (A B). Пусть
A и B — нечеткие подмножества. Будем говорить, что A
содержится в B, и обозначать A B, если x Е, A(x) B(x)
Равенство. A и B равны (A = B), если x Е, A(x) = B(x)
Слайд 17Множеством -уровня нечеткого множества А
является обычное множество А всех таких элементов универсального множества
Е,
степень принадлежности которых нечеткому множеству А больше или равна :
A = {x | x Е, A(x) }.
Множество -уровня называют иногда сечением нечеткого множества А. Причем, если A(x) , то говорят о сильном сечении, если A(x) > , то о слабом сечении.
Нечеткое множество А можно разложить по его множествам уровня следующим образом:
где A — произведение числа на множество A. Знак — знак объединения множеств A по .
Сечения нечеткого множества
Слайд 18Операции над нечеткими множествами
Функция принадлежности для объединения двух нечетких множеств
А и B с функциями принадлежности определена как максимум из
двух индивидуальных функций принадлежности. Это называется критерием максимума.
Объединением нечетких множеств А и В в Е называют наименьшее нечеткое подмножество A Y В, включающее как А, так и В, с функцией принадлежности вида: A Y B (x) = max(A(x), B(x)), x E
Слайд 19Пересечение
Функция принадлежности пересечения двух нечетких множеств А и B с
функциями принадлежности и определена как минимум из двух индивидуальных функций
принадлежности. Это называется критерием минимума.
Пересечением нечетких множеств А и В в Е называют наибольшее нечеткое подмножество А I В, содержащееся одновременно в А и В, с функцией принадлежности вида: A I B (x) = min(A(x), B(x)), x E
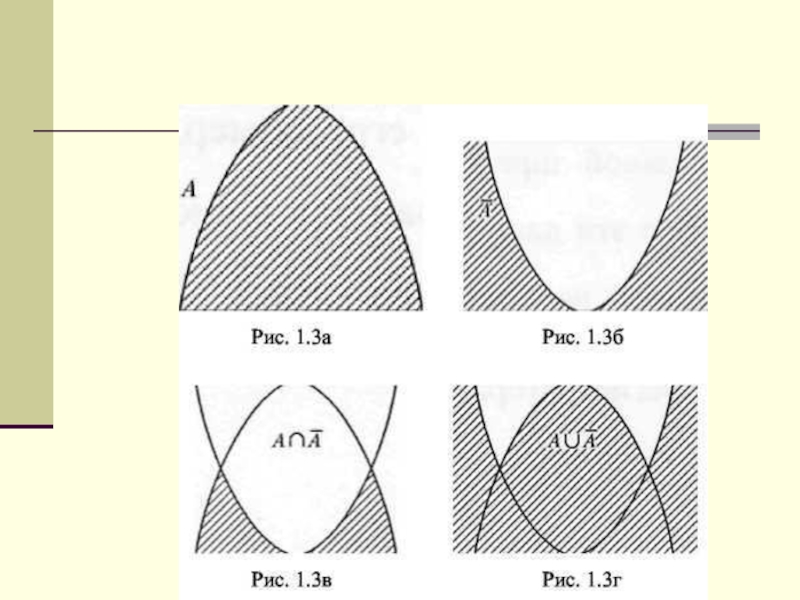
Слайд 20Дополнение
Функция принадлежности дополнения нечеткого множества А с функцией принадлежности определена
как отрицание данной функции членства. Это называется критерием отрицания
Дополнением
нечеткого множества А называют нечеткое множество A с функцией принадлежности: A (x) = 1 A(x), x E
Слайд 21Разность нечетких множеств А и В определяется по-разному, введением двух
независимых операций
или A B (x) =
min(A(x), 1 B(x)), x E
Дизъюнктивная сумма А В нечетких множеств А и В определяется как
A B (x) = max[ min(A(x), 1 B(x) ), min(B(x), 1 A(x))] x E
Слайд 26Алгебраические операции
Алгебраическое произведение А и В обозначается
определяется функцией принадлежности вида
A B (x) = A(x) B(x), x E
Алгебраическая сумма
этих множеств обозначается А+В и определяется функцией принадлежности
A+ B (x) = A(x) + B(x) — A(x) B(x), x E
Степенью нечеткого множества A называется нечеткое множество Aα с функцией принадлежности µAα (x) = µαA (x), x E, α>0.
Слайд 27Операции концентрирования, растяжения и контрастной интенсификации
При α = 2 получаем
операцию концентрирование (уплотнение) (CON):
CON(A) = A2
В результате
применения этой операции к множеству А снижается степень нечеткости описания, причем для элементов с высокой степенью принадлежности это уменьшение относительно мало, а для элементов с малой степенью принадлежности относительно велико.
При α = 0.5 получаем операцию растяжения (DIL):
DIL(A) = A0.5
Эта операция увеличивает степень нечеткости исходного нечеткого множества.
Операция контрастной интенсификации (INT) определяется с помощью функции принадлежности следующим образом:
Умножение на число.
Слайд 28Декартово (прямое) произведение. Пусть А1, А2, … Аn нечеткие подмножества
универсальных множеств U1, U2, … Un соответственно.
Декартово произведение А=А1 ×
А2 ×…× Аn является нечетким подмножеством декартового произведения U = U1 ×U2 ×…×Un c функцией принадлежности вида:
A(x) = min(A1(x1), …, An(xn)), x = (x1, …, xn) U
Слайд 29Расстояние между нечеткими множествами
неотрицательность;
симметричность;
транзитивность
Расстояние Хэмминга
Относительное расстояние Хэмминга:
Слайд 30Евклидово или квадратичное расстояние
Относительное евклидово расстояние
Слайд 31Индексы нечеткости
Обычное подмножество, ближайшее к нечеткому
Линейный индекс нечеткости
Квадратичный индекс нечеткости
Слайд 32Нечеткие отношения
Нечеткие отношения играют фундаментальную роль в теории нечетких
систем. Аппарат теории нечетких отношений используется при построении теории нечетких
автоматов, при моделировании структуры сложных систем, при анализе процессов принятия решений
Обычное неразмытое n-арное отношение R определяется как подмножество декартова произведения множеств
Нечеткое отношение можно задать с помощью его функции принадлежности
Слайд 33Бинарные нечеткие отношения
Далее мы ограничимся рассмотрением лишь бинарных нечетких отношений,
являющихся отображением на отрезок [0,1], т.е.
Если множества A и
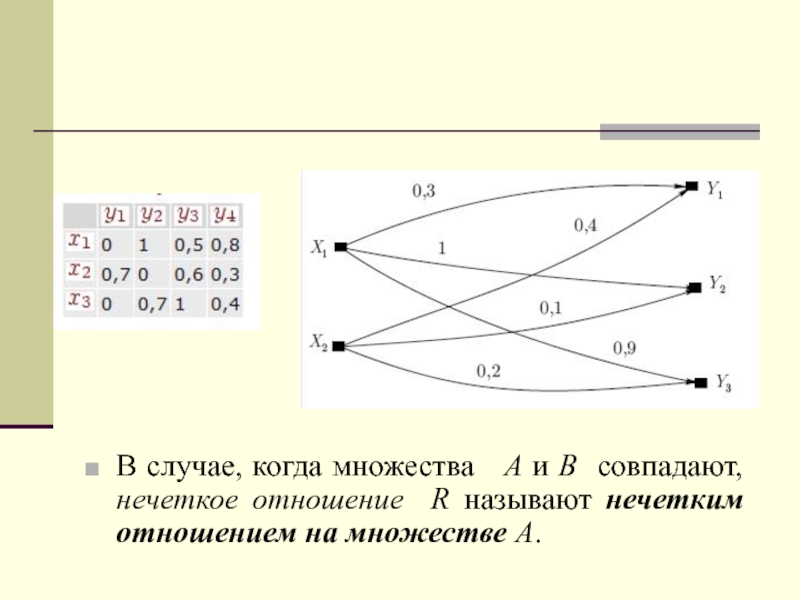
B конечны, нечеткое отношение R между A и B можно представить с помощью его матрицы отношения, первой строке и первому столбцу которой ставятся в соответствие элементы множеств A и B, а на пересечении a-той строки и b-го столбца помещается элемент
Слайд 34В случае, когда множества A и B совпадают, нечеткое
отношение R называют нечетким отношением на множестве A.


























![Нечеткие множества Бинарные нечеткие отношенияДалее мы ограничимся рассмотрением лишь бинарных нечетких отношений, являющихся Бинарные нечеткие отношенияДалее мы ограничимся рассмотрением лишь бинарных нечетких отношений, являющихся отображением на отрезок [0,1], т.е. Если](/img/thumbs/b5c2a5201ab9529ed06349c158f60d68-800x.jpg)