Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Объём геометрических тел 11 класс
Содержание
- 1. Объём геометрических тел 11 класс
- 2. Рассмотрим произвольную треугольную пирамиду SABC с высотой
- 3. hHИспользуя понятие бесконечной интегральной суммы, объем данной
- 4. На основании предыдущих рассуждений можно сделать вывод
- 5. ABCB1A1C1CA1BРассмотрим произвольную треугольную призму ABCA1B1C1.Разобьем её на
- 6. ACB1A1C1CA1BBТеперь разобьём четырёхугольную пирамиду A1BCC1B1 секущей плоскостью
- 7. ACB1A1C1CA1BBA1C1BУ треугольных пирамид A1ABC и BA1B1C1 основания
- 8. ACB1A1C1CA1BBA1C1BТогда, по свойству транзитивности, объемы всех трех
- 9. hHhЭту же формулу можно было получить непосредственным
- 10. Рассматривая произвольную n-угольную пирамиду SA1A2…An как сумму
- 11. Итак, для любой n-угольной пирамиды:,где Sосн. – площадь основания пирамиды, H – высота пирамиды.
- 12. Скачать презентанцию
Рассмотрим произвольную треугольную пирамиду SABC с высотой SO=H.ABCSOHO1hПостроим сечение пирамиды, параллельное плоскости основания и находящееся на расстоянии h от её вершины.Т.к. ΔABCA1B1C1, то по свойству площадей подобных фигур :A1C1B1h ∈[0; H
Слайды и текст этой презентации
Слайд 1Объём геометрических тел.
Урок в 11 классе
Учитель Расихина Л.В.
МБОУ СОШ №1
ст. Староминской Краснодарского края
Слайд 2
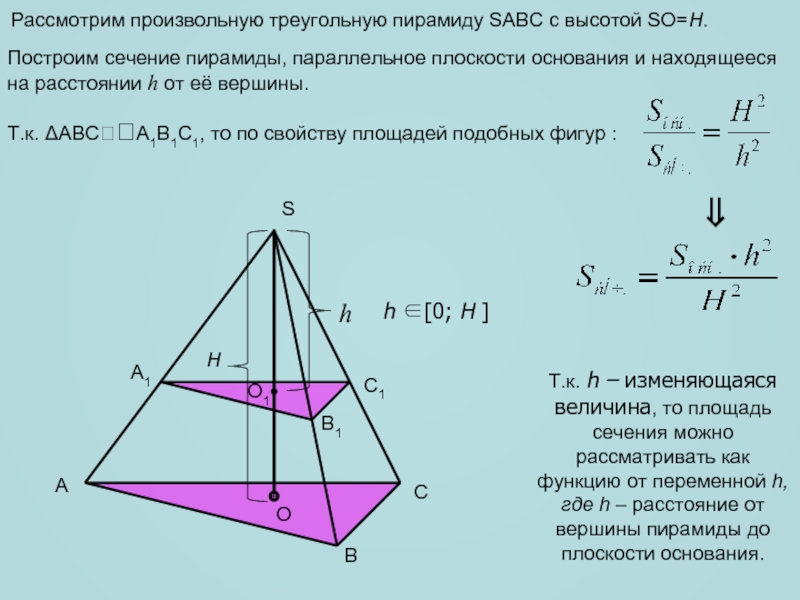
Рассмотрим произвольную треугольную пирамиду SABC с высотой SO=H.
A
B
C
S
O
H
O1
h
Построим сечение пирамиды,
параллельное плоскости основания и находящееся на расстоянии h от её
вершины.Т.к. ΔABCA1B1C1, то по свойству площадей подобных фигур :
A1
C1
B1
h ∈[0; H ]
⇒
Т.к. h – изменяющаяся величина, то площадь сечения можно рассматривать как функцию от переменной h, где h – расстояние от вершины пирамиды до плоскости основания.
Слайд 3
h
H
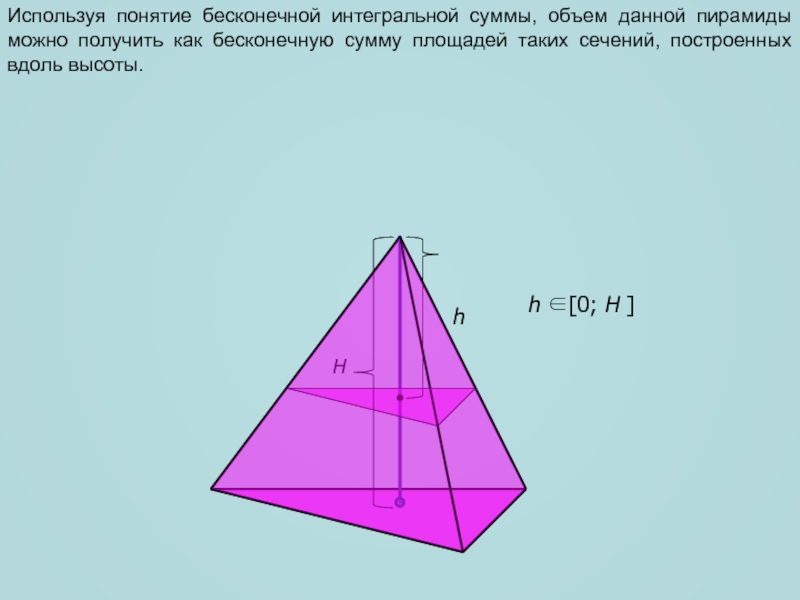
Используя понятие бесконечной интегральной суммы, объем данной пирамиды можно получить
как бесконечную сумму площадей таких сечений, построенных вдоль высоты.
h ∈[0;
H ]
Слайд 4
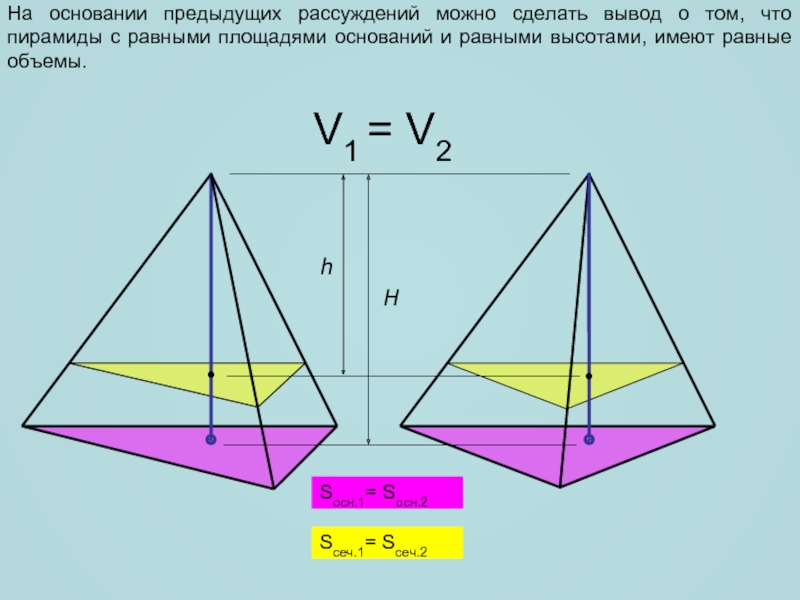
На основании предыдущих рассуждений можно сделать вывод о том, что
пирамиды с равными площадями оснований и равными высотами, имеют равные
объемы.H
Sосн.1= Sосн.2
V1 = V2
h
Sсеч.1= Sсеч.2
Слайд 5
A
B
C
B1
A1
C1
C
A1
B
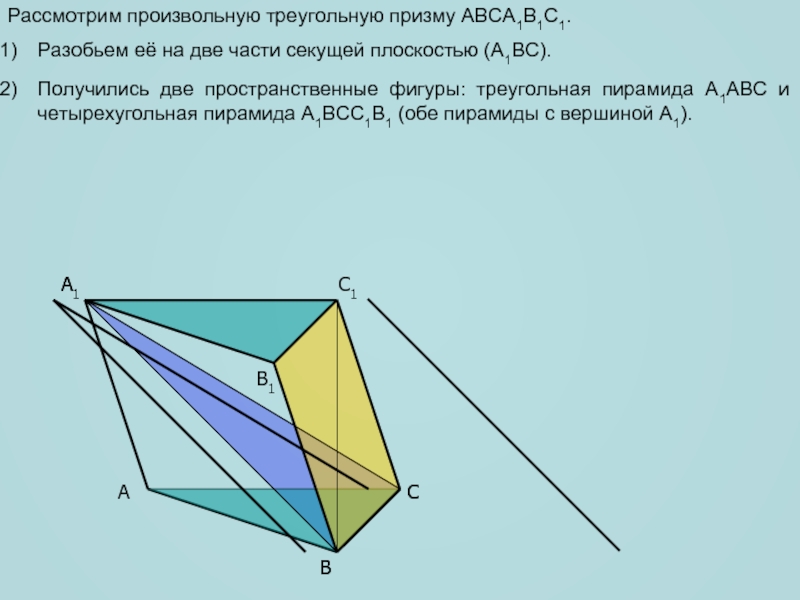
Рассмотрим произвольную треугольную призму ABCA1B1C1.
Разобьем её на две части секущей
плоскостью (A1BC).
Получились две пространственные фигуры: треугольная пирамида A1ABC и четырехугольная
пирамида A1BCC1B1 (обе пирамиды с вершиной A1).
Слайд 6
A
C
B1
A1
C1
C
A1
B
B
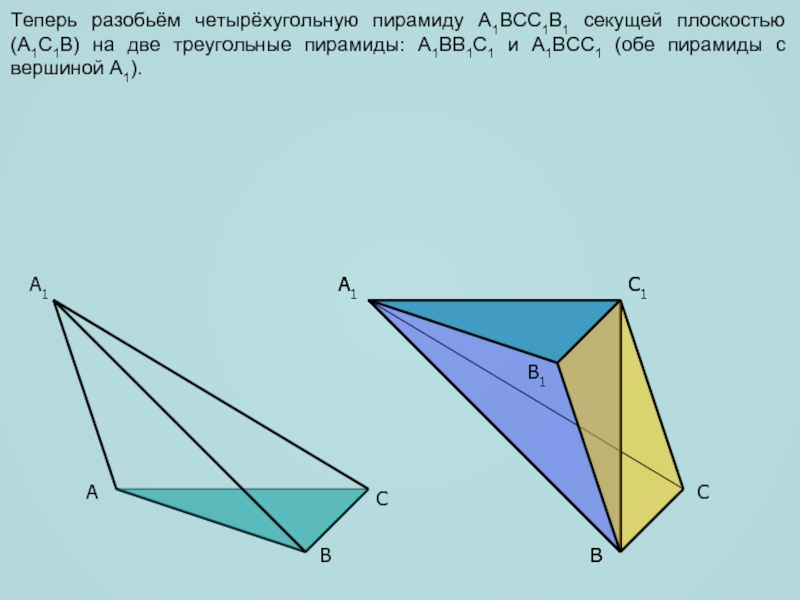
Теперь разобьём четырёхугольную пирамиду A1BCC1B1 секущей плоскостью (A1C1B) на две
треугольные пирамиды: A1BB1C1 и A1BCC1 (обе пирамиды с вершиной A1).
A1
C1
B
Слайд 7
A
C
B1
A1
C1
C
A1
B
B
A1
C1
B
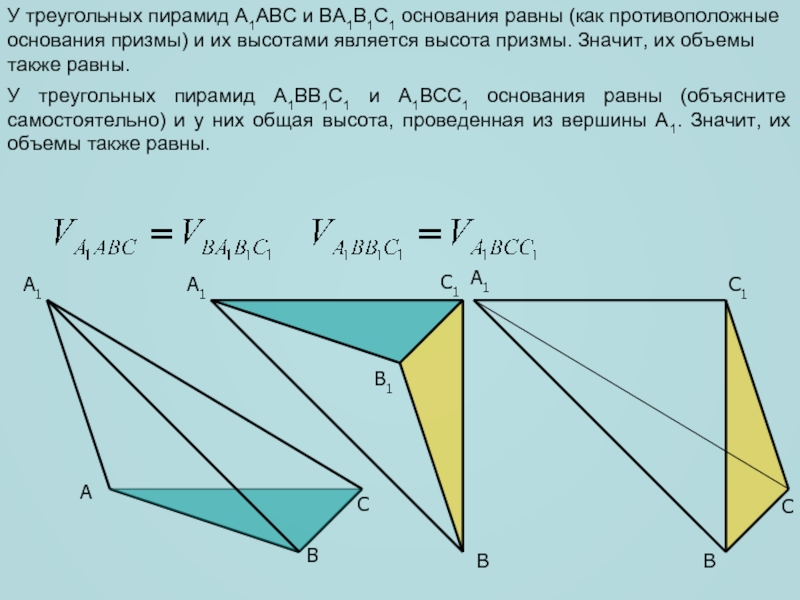
У треугольных пирамид A1ABC и BA1B1C1 основания равны (как противоположные
основания призмы) и их высотами является высота призмы. Значит, их
объемы также равны.У треугольных пирамид A1BB1C1 и A1BCC1 основания равны (объясните самостоятельно) и у них общая высота, проведенная из вершины A1. Значит, их объемы также равны.
Слайд 8
A
C
B1
A1
C1
C
A1
B
B
A1
C1
B
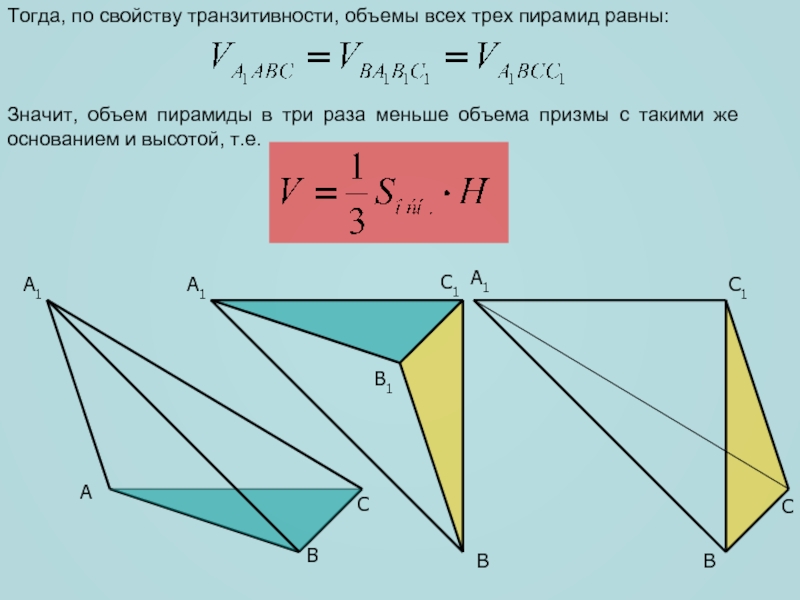
Тогда, по свойству транзитивности, объемы всех трех пирамид равны:
Значит, объем
пирамиды в три раза меньше объема призмы с такими же
основанием и высотой, т.е.
Слайд 9
h
H
h
Эту же формулу можно было получить непосредственным интегрированием площади сечения,
как функции, зависящей от расстояния h:
h ∈[0; H ]
0
Слайд 10
Рассматривая произвольную n-угольную пирамиду SA1A2…An как сумму треугольных пирамид с
общей вершиной и высотой, получим формулу для нахождения объема любой
пирамиды:S
A3
An
A2
A1
H
Слайд 11
Итак, для любой n-угольной пирамиды:
,где Sосн. – площадь основания пирамиды,
H – высота пирамиды.
Теги
