Слайд 1
Основные характеристики цифрового видео
Цифровое видео имеет пять основных характеристик:
экранное
разрешение, частота кадров, глубина цвета, битрейт , качество изображения.
Экранное
разрешение (Resolution) – обозначает количество точек (пикселей) по горизонтали и вертикали, из которых состоит изображение (видеокадр) на экране. При записи разрешения сначала указывается значение количества точек в строке (горизонтальное разрешение), а затем число строк, участвующих в построении изображения (вертикальное разрешение).
Например, для европейского видеостандарта PAL размер кадра составлял 720x576 пикселей, для североамериканского стандарта NTSC – 720x480, для видео высокой четкости (HD 720p) – 1280х720, а для новомодного стандарта HDTV (Full HD) – 1920x1080 точек.
Чем выше экранное разрешение, тем качество видео лучше.
Слайд 2Частота кадров – величина указывающая, на то, какое количество кадров сменяется
за секунду.
Глубина цвета (цветовое разрешение) – характеристика, указывающая количество цветов,
которые могут участвовать в формировании видеоизображения. Количество цветов в цифровом видео измеряется в битах. Так 1 бит может принимать два разных значения (0 или 1) и позволяет соответственно закодировать только два цвета (обычно черный и белый). С помощью двух бит можно закодировать уже 4 цвета (22 = 4), с помощью трех бит – 8 цветов (23), четырёх – 16 (24) и так далее.
Как правило, цветовое разрешение описывается с помощью специальных цветовых моделей. В компьютерной технике применяется модель RGB (красный-зеленый-синий), которая может быть представлена следующими наиболее распространенными режимами глубины цвета: 8 бит (256 цветов), 16 бит (65 536 цветов) и 24 бита (16 777 216 цветов).
Человеческий глаз, по разным источникам, может воспринять от 5 до 10 миллионов цветовых оттенков.
Слайд 3Битрейт (ширина видеопотока) – показывает количество обрабатываемых бит видеоинформации за одну
секунду времени. Иначе говоря – это скорость видеопотока, которая измеряется
в мегабитах в секунду (Мбит/с).
Чем выше скорость видеопотока, тем лучше качество.
Например, для стандарта DVD-видео ширина потока составляет около 5 Мбит/c, а для формата телевидения высокой четкости HDTV – уже 10 Мбит/с.
Наиболее часто значение битрейта используется для оценки качества передаваемого видео через Интернет
Слайд 4Качество изображения – характеристика позволяющая оценить качество обработанного видео в сравнении
с оригиналом -- определяется совокупностью значений разрешения, глубины цвета и
скорости видеопотока
Стандарты сжатия
Одна минута чистого несжатого оцифрованного звука занимает на жестком диске компьютера около 10 Мбайт, вследствие этого, музыкальные файлы хранятся в сжатом виде,
Одна минута несжатого видео.
Для размещения 60-секундного ролика с частотой 30 кадров в секунду, разрешением 720x576 пикселей и 16-битной глубиной цвета требуется около полутора гигабайт свободного дискового пространства! ( без учета звуковой дорожки).
Цифровое видео хранится в наших компьютерах исключительно в сжатом виде.
Слайд 5DV (Digital Video) – один из самых первых алгоритмов сжатия для
видеопотока, разработка которого началась в 1993 году совместно сразу несколькими
компаниями, являющимися крупнейшими производителями видеооборудования (Sony, JVC, Panasonic, Philips и Hitachi).
Формат DV обеспечивает невысокую степень сжатия данных (5:1) и характеризуется высоким битрейтом, за счет чего выходящий видеофайл получается довольно большого размера. Одна минута DV-видео занимает около 200 Мб (1 час – 12 Гб) на цифровых носителях информации.
Наиболее часто этот формат используется для сжатия при видеосъемке с помощью бытовых цифровых камер и профессиональных камкордеров. При этом из-за небольшого коэффициента сжатия отснятые материалы получаются очень высокого качества, а сама процедура компрессии, которая происходит в реальном времени, не требует мощных технических компонентов.
Слайд 6MPEG
МPEG (Moving Picture Experts Group) – целое семейство стандартов сжатия цифровой
информации, разработанное и стандартизированное одноименной экспертной группой специалистов, сформированной организацией
ISO в далеком 1988 году.
Исходный стандарт видео и аудио компрессии MPEG-1,
Использование для кодирования алгоритмов MPEG-1 позволило получать видеопоток шириной до 1,5 Мбит в секунду с разрешением кадра 352x288 точек для PAL или 352x240 для NTSC, после чего на обычном CD может уместиться 74 минуты видео со звуком качества VHS (как у обычного видеомагнитофона).
В 1993 году при участии компаний JVC и Philips, была разработана его спецификация Video CD (VCD), которая известна многим пользователям. Из названия видно, что VCD является форматом для хранения сжатого видео со звуком на обычных компакт дисках.
В 1995 году появился популярнейший стандарт MPEG-2, который впоследствии получил широкое распространение в цифровых видеодисках DVD, а так же при передаче сигнала кабельного и спутникового телевидения
Слайд 7Максимальная емкость двухслойного DVD диска (DVD-9) составляет 8,5 Гбайт, на
который можно записать до трех часов видео с полным качеством.
При этом, средняя максимальная ширина потока равна 9,8 Мбит/с, что практически в 7 раз выше, чем у Video CD. Еще одним неоспоримым преимуществом MPEG-2 является возможность сохранения пятиканальной аудиодорожки (Dolby Digital 5.1 и DTS) .
Качество картинки здесь значительно выше, чем у предшественника: при 25 кадрах в секунду, разрешение составляло 720x576 точек для системы PAL, а для системы NTSC – 720х480 при 30 кадрах/с.
Слайд 8Наконец, в 1998 году появилось новое семейство форматов сжатия видео
– MPEG-4. Разрабатывалось оно с целью улучшения качества картинки при низкой
скорости потока.
Прежний стандарт MPEG-2, рассчитанный на высокий битрейт, с этой задачей справиться не мог, так что алгоритмы сжатия пришлось серьезно модифицировать.
Так же MPEG-2 не походит и для хранения видео высокой четкости (HD) с разрешениями от 1280x720 (720p) до 1920x1080 пикселей (1080i или 1080p), которое все больше и больше набирает популярность.
На сегодняшний день MPEG-4 является основным стандартом сжатия мультимедиа контента,
Практически все современные фото и видеокамеры снимают в HD-качестве. Так что для сохранения видео с таких устройств на компьютер, в любом случае придется ориентироваться на кодеки семейства MPEG-4.
Слайд 9Кодеки
Выбор определенного алгоритма преобразования данных, позволяет сжать видео совершенно разными
инструментами или программными средствами, что дает на выходе абсолютно различные
результаты.
Разительно может отличаться качество и характеристики видео записанного на мобильный телефон, скачанного из сети видеоролика в HD-формате или фильма с Blu-Ray диска.
У одного может картинка оставлять желать лучшего, у другого хромать звук, а третий, наоборот – эталон качества. А ведь все они закодированы с использованием одного стандарта - MPEG-4.
Во многом, все эти отличия определяются кодеком – специальной программой, осуществляющей сжатие (кодирование) исходных материалов. При этом каждый из них использует свой собственный алгоритм, который влияет как на качество, так и на скорость кодирования.
Само слово «кодек» является сокращением от двух слов «кодер-декодер». Это значит, что кодек должен включать в себя не только модуль сжатия (кодер), но и просмотра (декодер).
Слайд 10MPEG-4 Part 2 ASP - один из первых алгоритмов, появившихся в
1999 году. Кодеки, построенные на его основе, обеспечивают довольно низкое
качество выходящих материалов.
Одними из самых ярких представителей кодеков, базирующихся на основе этих алгоритмов, являются знакомые многим пользователям, коммерческий DivX и его бесплатная альтернатива XviD.
MPEG-4 AVC или H.264 – один из самых последних и популярных алгоритмов, использующихся с успехом как для сжатия видео с низким разрешением, так и HD контента. Кстати, большинство высококачественных фильмов на дисках Blu-Ray кодируется именно этим кодеком. Так же он часто используется и в бытовых HD-видеокамерах (AVCHD).
У этого семейства кодеков существуют как бесплатные модификации, например, x.264, так и коммерческие варианты, входящие в состав популярных видеоредакторов (Adobe Premiere, Pinnacle Studio и другие).
VC-1 – кодек, разработанный компанией Microsoft и стандартизированный в 2006 году. В его основу положен собственный формат видеосжатия WMV (Windows Media Video) и система кодирования WMV 9.
Слайд 11H.265/HEVC
В последнее время интенсивно разгабатываются методы видеокодирования в рамках стандарта
H.265/HEVC, в которых принимаются во внимание параметры внутрикадрового и межкадрового
кодирования, анализа движения, квантования и статистического кодирования;
Особое внимание при видеокомпрессии уделяется алгоритмам многоканальной вейвлет-декомпозиции кадров видео
Для кодирования алгоритмов кодирования звуковых сигналов используются алгоритмы в рамках стандарта HE-AAC, включающие алгоритмы психоакустической звуковой модели, алгоритмы квантования, алгоритмы статистического кодирования.
Слайд 12Медиаконтейнеры и их форматы
Как и любая другая цифровая информация, видео
хранится на диске в виде файлов, или как их еще
называют, медиаконтейнеров, содержащих видео-, аудио и другие потоки, а так же метаданные.
AVI (Audio Video Interleave) – самый древний и традиционный из всех видов медиаконтейнеров.
MKV (Matroska или Матрёшка) – популярнейший формат мультимедийного контейнера, отвечающий всем современным требованиям. К его основным возможностям можно отнести:
создание экранного меню;
разбиение содержимого на главы;
быстрая перемотка по файлу;
переключение «на лету» между звуковыми и видеодорожками, а так же субтитрами.
MP4 (MPEG-4 Part 14) – еще один современный формат файлов для хранения цифровых видео и аудиопотоков, являющийся частью стандарта MPEG-4.
Слайд 13VOB (Versioned Object Base) – основной контейнер, используемый для хранения мультимедиа контента на
DVD-дисках.
FLV (Flash Video) – медиаконтейнер, использующийся для размещения и передачи видеороликов
в глобальной сети
MOV– формат файла, разработанный компанией Apple для хранения видео, графики, анимации и 3D. Своим появлением обязан технологии воспроизведения медиаконтента QuickTime.
TS и M2TS– специализированные контейнеры для хранения HD-видео. TS используется в потоковом вещании цифрового телевидения IPTV и DVB.
Слайд 14Добиться довольно значительного уровня сжатия аудио и видеоинформации удается при использовании
специальных методов, основанных на анализе структуры данных и последующим сжатием
с некоторыми потерями.
За время своего существования комитет (Moving Pictures Expert Group, группа экспертов в области движущихся изображений), выработал ряд стандартов по данному вопросу. В результате, после обобщения обширных исследований в этой области, группой был рекомендован ряд специфических форматов для хранения данных, отличных по качеству результатов и скорости потока данных.
Основанная идея, на которой основаны все методики сжатия аудио и видео сигнала с потерями, – пренебрежение тонкими деталями сигнала -оригинала, лежащие вне пределов которые воспринимает человеческое ухо и глаз..
Слайд 15Для звука
Пренебрежение тонкими деталями сигнала -оригинала
Далее деление полосы звуковых частот
на подполосы, каждая из которых в последствии обрабатывается отдельно. Программа
кодирования выделяет самые громкие звуки в каждой полосе и использует эту информацию для определения приемлемого уровня шума для этой полосы.
Звуковое сжатие базируется на простом факте – если человек находиться рядом с громко воющей сиреной, то вряд ли он услышит разговор стоящих неподалеку людей. Причем это происходит не оттого, что человек обращает большое внимание на громкий звук, а в большей степени оттого, что человеческое ухо фактически теряет звуки, лежащие в том же диапазоне частот, что и более громкий звук. Этот эффект носит название маскирующего,
Еще одним моментом кодирования звука является использование психоакустической модели, опирающейся на особенности человеческого восприятия звука. Сжатие с использованием этой модели основано на удалении заведомо неслышимых частот с более тщательным сохранением звуков, хорошо различаемых человеческим ухом
Слайд 16Видео
Все форматы сжатия семейства MPEG используют высокую избыточность информации в
изображениях, разделенных малым интервалом времени.
Между двумя соседними кадрами обычно
изменяется только малая часть сцены – например, происходит плавное смещение небольшого объекта на фоне фиксированного заднего плана. В этом случае полная информация о сцене сохраняется выборочно – только для опорных изображений.
Форматы сжатия семейства MPEG сокращают объем информации следующим образом:
-устраняется временная избыточность видео (учитывается только разностная информация);
-устраняется пространственная избыточность изображений путем подавления мелких деталей сцены;
-устраняется часть информации о цветности;
-повышается информационная плотность результирующего цифрового потока путем выбора оптимального математического кода для его описания.
Слайд 17Форматы сжатия MPEG сжимают только опорные кадры – I-кадры (Intra
frame – внутренний кадр). В промежутки между ними включаются кадры,
содержащие только изменения между двумя соседними I-кадрами – P-кадры (Predicted frame – прогнозируемый кадр). Для того чтобы сократить потери информации между I-кадром и P-кадром, вводятся так называемые B-кадры (Bidirectional frame – двунаправленный кадр).
В них содержится информация, которая берется из предшествующего и последующего кадров. При кодировании в форматах сжатия MPEG формируется цепочка кадров разных типов. Типичная последовательность кадров выглядит следующим образом:
I B B P B B I B B P B B I B B ...
Соответственно, последовательность кадров в соответствии с их номерами будет воспроизводиться в следующем порядке:
1 4 2 3 7 6 5 ...
Слайд 18
Критерии сравнения алгоритмов
Характеристики алгоритма компрессии зависят от конкретных условий, в
которые будет поставлен алгоритм.
Так, степень компрессии зависит от того, на каком классе изображений
алгоритм тестируется. Аналогично, скорость компрессии нередко зависит от того, на какой платформе реализован алгоритм. Преимущество одному алгоритму перед другим может дать, например, возможность использования в вычислениях алгоритма технологий нижнего уровня, типа ММХ, а это возможно далеко не для всех алгоритмов.
Наиболее важные критерии сравнения алгоритмов компрессии.
1. Худшая, средняя и лучшая степень сжатия.
То есть доля, на которую возрастет изображение, если исходные данные будут наихудшими; некая среднестатистическая степень для того класса изображений, на который ориентирован алгоритм; и, наконец, лучшая степень. Последняя необходима лишь теоретически, поскольку показывает степень сжатия наилучшего (как правило, абсолютно черного) изображения, иногда фиксированного размера.
Слайд 192. Класс изображений, на который ориентирован алгоритм
3. Симметричность. Отношение характеристики алгоритма кодирования к аналогичной
характеристике при декодировании. Характеризует ресурсоемкость процессов кодирования и декодирования.
4. Есть
ли потери качества? И если есть, то за счет чего изменяется степень сжатия? Дело в том, что у большинства алгоритмов сжатия с потерей информации существует возможность изменения степени сжатия.
5. Характерные особенности алгоритма и изображения, к которым его применяют. Здесь могут указываться наиболее важные для алгоритма свойства, которые могут стать определяющими при его выборе.
Слайд 20
Алгоритмы сжатия с потерями
Критерии сжатия
Одна из серьезных проблем машинной графики
заключается в том, что до сих пор не найден адекватный
критерий оценки потерь качества изображения. А теряется оно постоянно – при оцифровке, при переводе в ограниченную палитру цветов, при переводе в другую систему цветопредставления для печати, и при архивации с потерями.
1. Критерий: среднеквадратичное отклонение значений пикселей (L2 мера, или root mean square – RMS):
По нему изображение будет сильно испорчено при понижении яркости всего на 5% (глаз этого не заметит – у разных мониторов настройка яркости варьируется гораздо сильнее). В то же время изображения со “снегом” – резким изменением цвета отдельных точек, слабыми полосами или “муаром” будут признаны почти не изменившимися
Слайд 21.2. Критерий- максимальное отклонение:
Эта мера, как можно догадаться, крайне чувствительна
к биению отдельных пикселей. Т.е. во всем изображении может существенно измениться
только значение одного пикселя (что практически незаметно для глаза), однако согласно этой мере изображение будет сильно испорчено
3. Мера, которую сейчас используют на практике, называется мерой отношения сигнала к шуму (peak-to-peak signal-tо-noise ratio — PSNR):
Слайд 22JPEG
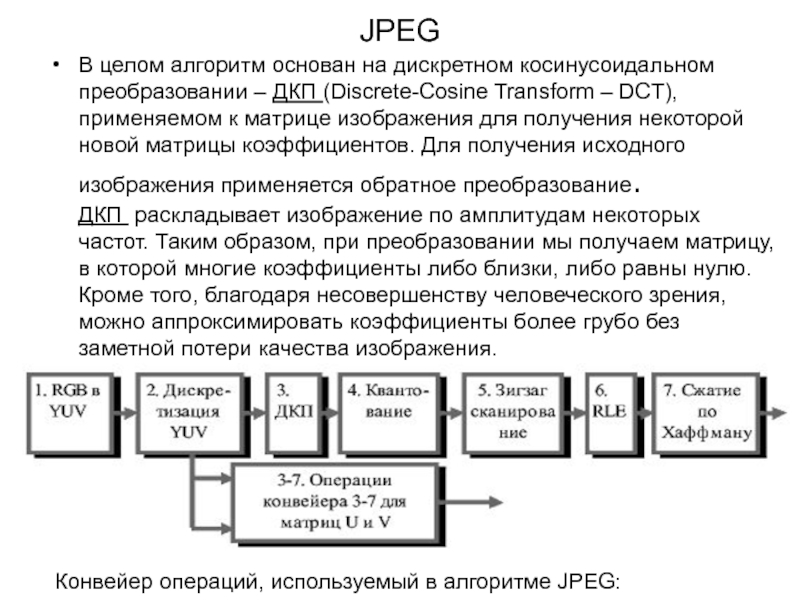
В целом алгоритм основан на дискретном косинусоидальном преобразовании – ДКП (Discrete-Cosine Transform
– DCT), применяемом к матрице изображения для получения некоторой новой
матрицы коэффициентов. Для получения исходного изображения применяется обратное преобразование. ДКП раскладывает изображение по амплитудам некоторых частот. Таким образом, при преобразовании мы получаем матрицу, в которой многие коэффициенты либо близки, либо равны нулю. Кроме того, благодаря несовершенству человеческого зрения, можно аппроксимировать коэффициенты более грубо без заметной потери качества изображения.
Конвейер операций, используемый в алгоритме JPEG:
Слайд 23Шаг 1.Перевод изображения из цветового пространства RGB, с компонентами, отвечающими
за красную (Red), зеленую (Green) и синюю (Blue) составляющие цвета
точки, в цветовое пространство YCrCb (иногда называют YUV).
Шаг 2. Разбитие исходного изображения на матрицы 8x8. Формирование из каждой три рабочие матрицы ДПК – по 8 бит отдельно для каждой компоненты.
Из исходной матрицы размером 16x16 получается только одна рабочая матрица ДКП. При этом, теряется 3/4 полезной информации о цветовых составляющих изображения и получается сразу сжатие в два раза.
Шаг 3.
В упрощенном виде ДКП при n=8 можно представить так:
Слайд 24Применяем ДКП к каждой рабочей матрице. При этом мы получаем
матрицу, в которой коэффициенты в левом верхнем углу соответствуют низкочастотной
составляющей изображения, а в правом нижнем – высокочастотной.
Шаг 4. Произведение квантования. Т.е деление рабочей матрицы на матрицу квантования поэлементно q[u,v] (МК)
.
На этом шаге осуществляется управление степенью сжатия, и происходят самые большие потери. Понятно, что, задавая МК с большими коэффициентами, мы получим больше нулей и, следовательно, большую степень сжатия.
Шаг 5. Переводим матрицу 8x8 в 64-элементный вектор при помощи "зигзаг"-сканирования, т.е. берем элементы с индексами (0,0), (0,1), (1,0), (2,0)...
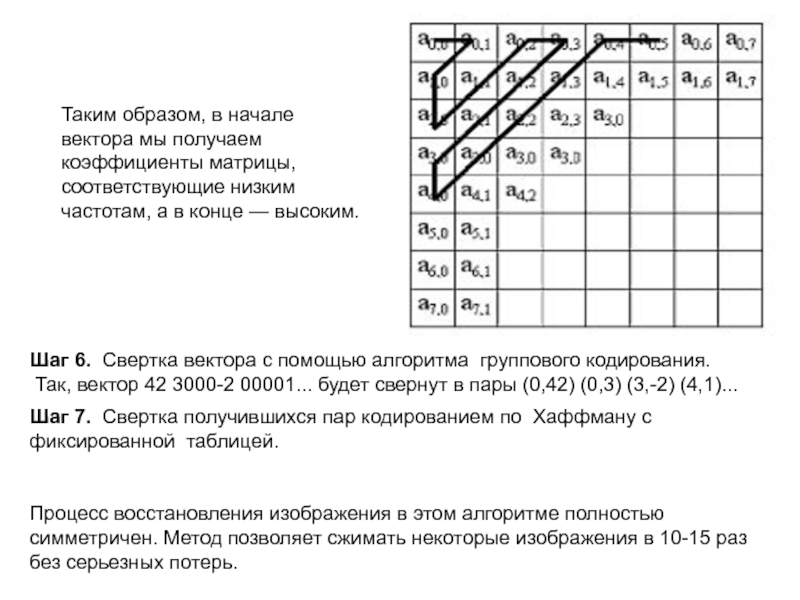
Слайд 25Таким образом, в начале вектора мы получаем коэффициенты матрицы, соответствующие
низким частотам, а в конце — высоким.
Шаг 6. Свертка вектора
с помощью алгоритма группового кодирования.
Так, вектор 42 3000-2 00001... будет свернут в пары (0,42) (0,3) (3,-2) (4,1)...
Шаг 7. Свертка получившихся пар кодированием по Хаффману с фиксированной таблицей.
Процесс восстановления изображения в этом алгоритме полностью симметричен. Метод позволяет сжимать некоторые изображения в 10-15 раз без серьезных потерь.
Слайд 26Существенными положительными сторонами алгоритма является то, что:
Задается степень сжатия.
Выходное цветное
изображение может иметь 24 бита на точку.
Отрицательными сторонами алгоритма является
то, что:
При повышении степени сжатия изображение распадается на отдельные квадраты (8x8). Это связано с тем, что происходят большие потери в низких частотах приквантовании, и восстановить исходные данные становится невозможно.
Проявляется эффект Гиббса – ореолы по границам резких переходов цветов.
Не очень приятным свойством JPEG является также то, что нередко горизонтальные и вертикальные полосы на дисплее абсолютно не видны и могут проявиться только при печати в виде муарового узора. Он возникает при наложении наклонного растра печати на горизонтальные и вертикальные полосы изображения.
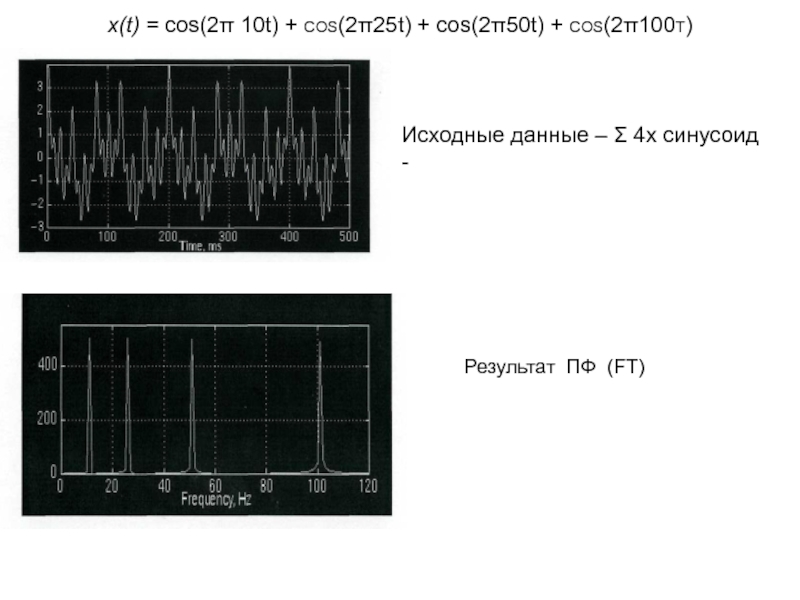
Слайд 28x(t) = cos(2π 10t) + cos(2π25t) + cos(2π50t) + cos(2π100t)
Исходные
данные – Σ 4х синусоид
-
Результат ПФ (FT)
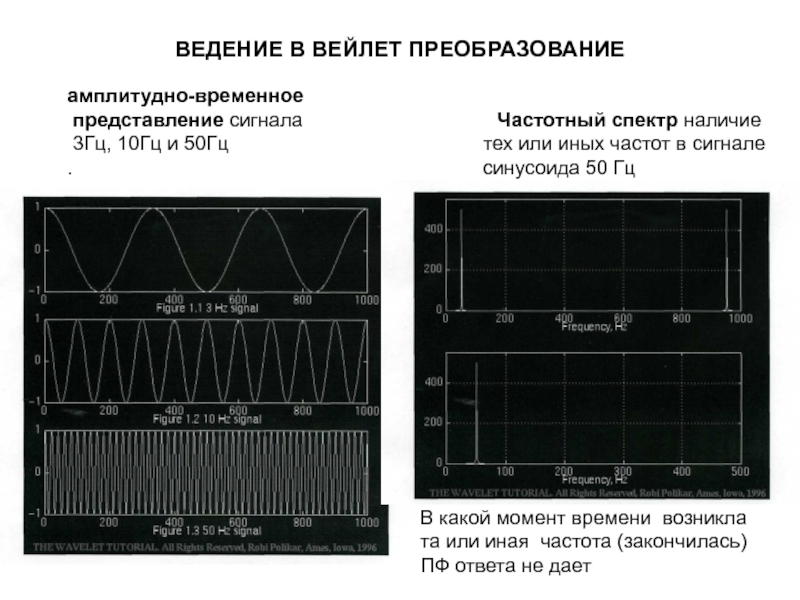
Слайд 29ВЕДЕНИЕ В ВЕЙЛЕТ ПРЕОБРАЗОВАНИЕ
амплитудно-временное
представление сигнала
Частотный спектр наличие
3Гц, 10Гц и 50Гц тех или иных частот в сигнале
. синусоида 50 Гц
В какой момент времени возникла та или иная частота (закончилась) ПФ ответа не дает
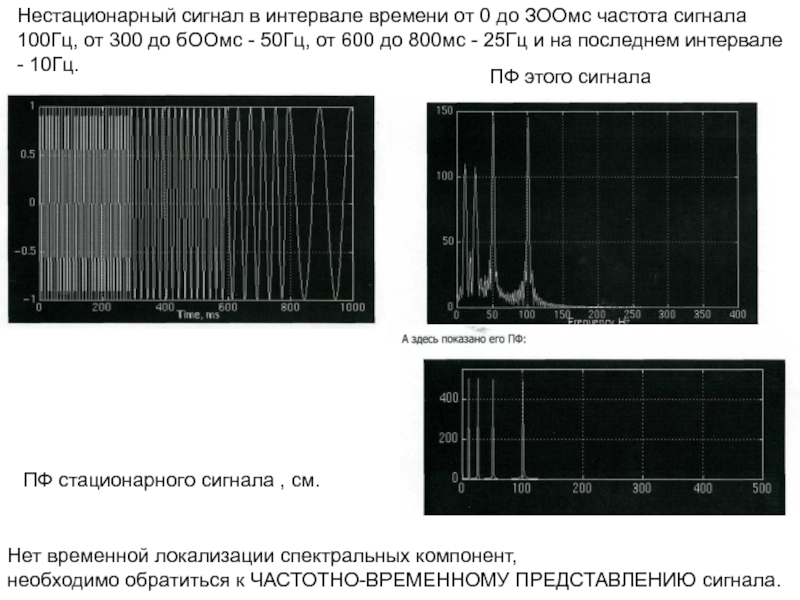
Слайд 30Нестационарный сигнал в интервале времени от 0 до ЗООмс частота
сигнала 100Гц, от 300 до бООмс - 50Гц, от 600
до 800мс - 25Гц и на последнем интервале - 10Гц.
ПФ этого сигнала
ПФ стационарного сигнала , см.
Нет временной локализации спектральных компонент,
необходимо обратиться к ЧАСТОТНО-ВРЕМЕННОМУ ПРЕДСТАВЛЕНИЮ сигнала.
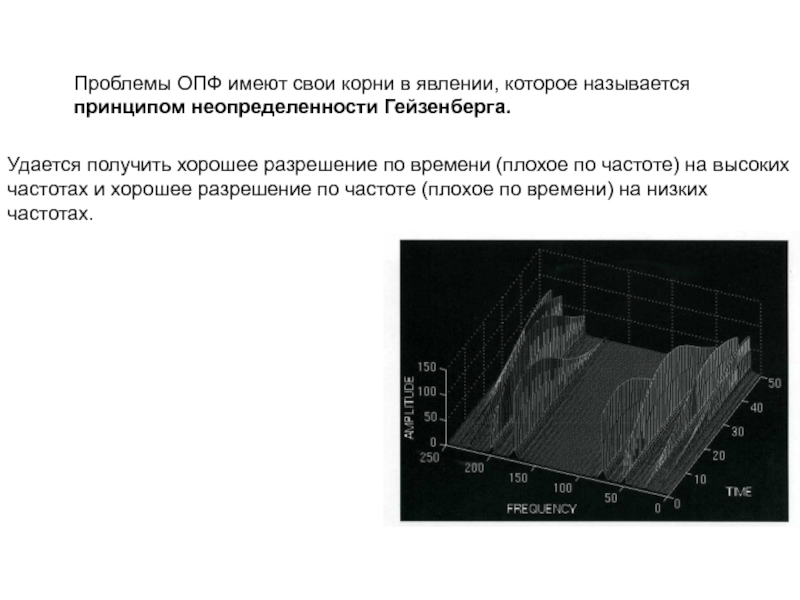
Слайд 31Проблемы ОПФ имеют свои корни в явлении, которое называется принципом
неопределенности Гейзенберга.
Удается получить хорошее разрешение по времени (плохое по
частоте) на высоких частотах и хорошее разрешение по частоте (плохое по времени) на низких частотах.
Слайд 32НЕОБХОДИМОСТЬ получить частотно- временное представление о сигнале
Уже в 1910 году
А.Хаар опубликовал полную ортонормальную систему базисных функций с локальной областью
определения (теперь они называются вейвлетами Хаара).
Первое упоминание о вейвлетах появилось в литературе по цифровой обработке и анализу сейсмических сигналов (работы А.Гроссмана и Ж.Морле). В последнее время возникло и оформилось целое научное направление,
Вейвлеты широко применяются для фильтрации и предварительной обработки данных, анализа состояния и прогнозирования ситуации на фондовых рынках, распознавания образов, при обработке и синтезе различных сигналов, например речевых, медицинских, для решения задач сжатия и обработки изображений, при обучении нейросетей и во многих других случаях, связанных с вейвлет-анализом и теорией вейвлет-преобразования
Слайд 33Главная задача
Такая Задача возникает всегда - , начиная от записи
показаний датчика и кончая оцифрованной речью или изображением, когда требуется
провести многомасштабный анализ (multiscale analysis, multiresolutional analysis) , который заключается в том, чтобы взглянуть на сигнал сначала вплотную – под микроскопом, затем через лупу, потом посмотреть на него издалека.
Это дает возможность - путем последовательного огрубления (или уточнения) сигнала выявлять его локальные особенности (ударение в речи или характерные детали изображения) и подразделять их по интенсивности.
Кроме того, таким образом, обнаруживается динамика изменения сигнала в зависимости от масштаба. Если резкие скачки (например, аварийное отклонение показаний датчика) во многих случаях видны "невооруженным глазом", то взаимодействия событий на мелких масштабах, не всегда.
Сосредоточившись только на мелких деталях, можно не заметить явлений, происходящих на глобальном уровне.
Слайд 34Введение в Вэйвлет преобразование (WT)
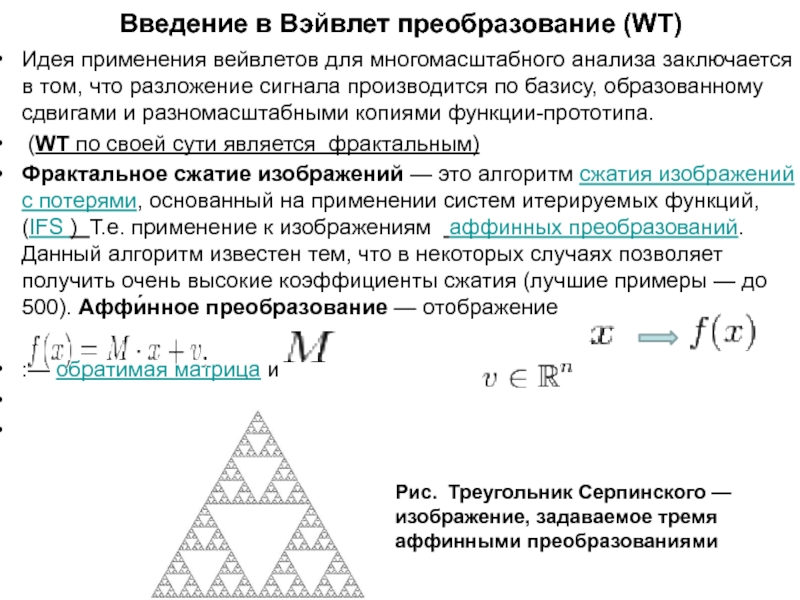
Идея применения вейвлетов для многомасштабного анализа
заключается в том, что разложение сигнала производится по базису, образованному
сдвигами и разномасштабными копиями функции-прототипа.
(WT по своей сути является фрактальным)
Фрактальное сжатие изображений — это алгоритм сжатия изображений c потерями, основанный на применении систем итерируемых функций, (IFS ) Т.е. применение к изображениям аффинных преобразований. Данный алгоритм известен тем, что в некоторых случаях позволяет получить очень высокие коэффициенты сжатия (лучшие примеры — до 500). Аффи́нное преобразование — отображение
:— обратимая матрица и
Рис. Треугольник Серпинского — изображение, задаваемое тремя аффинными преобразованиями
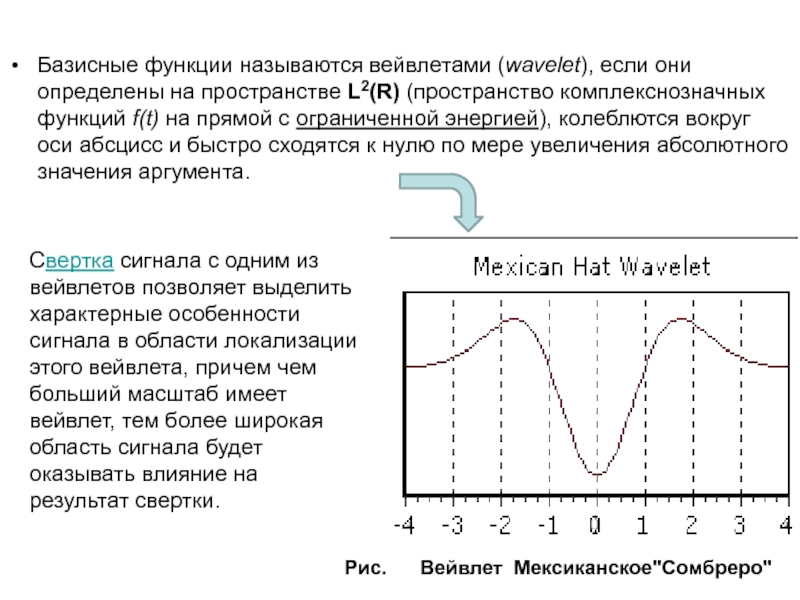
Слайд 35Базисные функции называются вейвлетами (wavelet), если они определены на пространстве
L2(R) (пространство комплекснозначных функций f(t) на прямой с ограниченной энергией),
колеблются вокруг оси абсцисс и быстро сходятся к нулю по мере увеличения абсолютного значения аргумента.
Свертка сигнала с одним из вейвлетов позволяет выделить характерные особенности сигнала в области локализации этого вейвлета, причем чем больший масштаб имеет вейвлет, тем более широкая область сигнала будет оказывать влияние на результат свертки.
Рис. Вейвлет Мексиканское"Сомбреро"
Слайд 36Чем лучше функция сконцентрирована во времени, тем больше она размазана
в частотной области (принцип неопределенности).
Вэйвлеты позволяют хорошо локализовать низкочастотные
детали сигнала в частотной области (преобладающие гармоники), а высокочастотные – во временной (резкие скачки, пики и т.п.), и решить Задачу –исследования последовательности, называмой временным или динамическим рядом (наблюдения за изменением свойств системы через одинаковые промежутки времени- например, состояние атмосферы (температура, влажность, давление), электрокардиограмма (ЭКГ) пациента в больнице, курсы валют.
Данные надо представить в каком-нибудь удобном для обработки виде
Дискретное Фурье-преобразование позволяет свернуть большое число значений временного ряда в несколько коэффициентов, но при этом пропадает временная составляющая – из зависимости амплитуды от времени мы получаем зависимость амплитуды от частоты.
Слайд 37ПРЕИМУЩЕСТВО WT
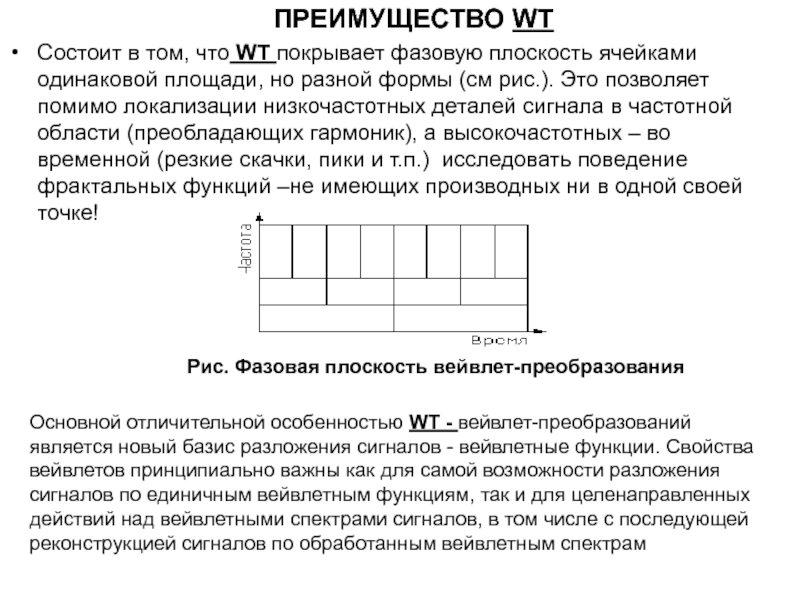
Состоит в том, что WT покрывает фазовую плоскость ячейками
одинаковой площади, но разной формы (см рис.). Это позволяет помимо
локализации низкочастотных деталей сигнала в частотной области (преобладающих гармоник), а высокочастотных – во временной (резкие скачки, пики и т.п.) исследовать поведение фрактальных функций –не имеющих производных ни в одной своей точке!
Основной отличительной особенностью WT - вейвлет-преобразований является новый базис разложения сигналов - вейвлетные функции. Свойства вейвлетов принципиально важны как для самой возможности разложения сигналов по единичным вейвлетным функциям, так и для целенаправленных действий над вейвлетными спектрами сигналов, в том числе с последующей реконструкцией сигналов по обработанным вейвлетным спектрам
Рис. Фазовая плоскость вейвлет-преобразования
Слайд 38Вейвлеты могут быть ортогональными, полуортогональными, биортогональными. Вейвлетные функции могут быть
симметричными, асимметричными и несимметричными, с компактной областью определения и не
имеющие таковой, а также иметь различную степень гладкости.
Некоторые вэйвлет функции имеют аналитическое выражение, другие – быстрый алгоритм вычисления вейвлет-преобразования. Для практики желательно было бы иметь ортогональные симметричные и асимметричные вейвлеты,
Наибольшее применение находят биортогональные вейвлеты.
Слайд 39Базисные функции вейвлет-преобразования
Различают вейвлеты по целевым задачам вейвлетных преобразований
с позиций декомпозиции – реконструкции сигналов и с позиции полной
информационной эквивалентности вейвлетного спектра сигналам временного (динамического, координатного) представления.
Определение вейвлета. К вейвлетам относятся локализованные функции, которые конструируются из одного материнского вейвлета Ψ(t) (или по любой другой независимой переменной) путем операций сдвига по аргументу (b) и масштабного изменения (а):
ψ ab(t) = (1/ ) ψ ((t-b)/a), (a, b)R, ψ(t)L2(R).
где множитель (1/ ) обеспечивает независимость нормы функций от масштабного числа 'a'.
НЕПРЕРЫВНОЕ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЕ СИГНАЛА
s(t)L2(R),
CWT применяется для качественного частотно-временного анализа, по смыслу соответствует преобразованию Фурье с заменой гармонического базиса exp(-jwt) на вейвлетный ψ((t-b)/a):
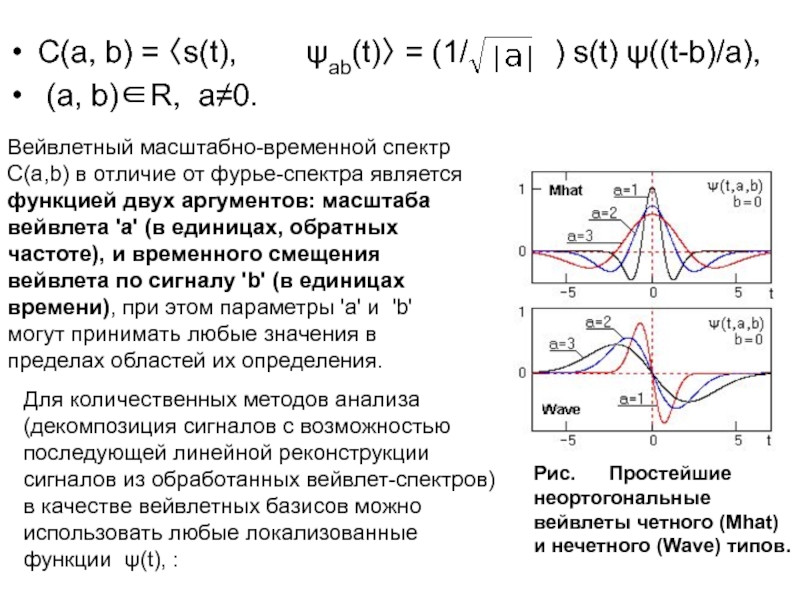
Слайд 40С(a, b) = s(t), ψab(t) = (1/
) s(t) ψ((t-b)/a),
(a, b)R,
a0.
Вейвлетный масштабно-временной спектр С(a,b) в отличие от фурье-спектра является функцией двух аргументов: масштаба вейвлета 'а' (в единицах, обратных частоте), и временного смещения вейвлета по сигналу 'b' (в единицах времени), при этом параметры 'а' и 'b' могут принимать любые значения в пределах областей их определения.
Рис. Простейшие неортогональные вейвлеты четного (Mhat) и нечетного (Wave) типов.
Для количественных методов анализа (декомпозиция сигналов с возможностью последующей линейной реконструкции сигналов из обработанных вейвлет-спектров) в качестве вейвлетных базисов можно использовать любые локализованные функции ψ(t), :
Слайд 41Если {ψ ab(t)} и {ψ #ab(t)}
функции-двойники и могут образовывать парные
базисы функционального пространства L2(R) то они позволяют представить любую произвольную функцию в пространстве L2(R) в виде ряда:
s(t) = С(a,b) Ψ#ab(t), (a, b)I,
Пара двойников формирует семейства { Ψmk(t)} и {Ψ#zp(t)}, удовлетворяющие условию биортогональности на целых числах I:
Ψmk(t), Ψ#zp(t) = dmz·dkp, m,k,z,p I,
возможно разложение сигналов на вейвлетные ряды с обратной формулой реконструкции.
СВОЙСТВА ВЕЙВЛЕТА,
Локализация. Вейвлет должен быть непрерывным, интегрируемым, иметь компактный носитель и быть локализованным как во времени (в пространстве), так и по частоте.
Слайд 42Свойства вейвлета,
Если вейвлет в пространстве сужается, то его "средняя"
частота повышается, спектр вейвлета перемещается в область более высоких частот
и расширяется. Этот процесс должен быть линейным – сужение вейвлета вдвое должно повышать его "среднюю" частоту и ширину спектра также вдвое
Вейвлетную функцию можно считать хорошо локализованной при выполнении условий:
Ψ(t) ≤ C/(1+|t|)1+e, Ψ(f) ≤ C/(1+|f|)1+e, С=const, при e > 0.
Нулевое среднее значение, т.е. выполнение условия для нулевого момента:
Ψ(t) dt = 0,
Это обеспечивает выделение локальных особенностей сигналов в пределах вейвлетного носителя на уровне региональных изменений и тренда, нулевого усиления постоянной составляющей сигналов, нулевого значеня частотного спектра вейвлета при ω=0, и локализацию спектра вейвлета в виде полосового фильтра с центром на определенной (доминирующей) частоте ω0.
.
Слайд 43Свойства вейвлета,
Ограниченность. Необходимое и достаточное условие:
||Ψ(t)||2 =
|Ψ(t)|2 dt <
Автомодельность базиса или самоподобие
Форма всех
базисных вейвлетов Ψab(t) должна быть подобна материнскому вейвлету Ψ(t), т.е. должна оставаться одной и той же при сдвигах и масштабировании (растяжении/сжатии), иметь одно и то же число осцилляций.
WT несет избыточную информацию о сигнале, так как каждая точка фазовой плоскости оказывает влияние на его результат.
Для точного восстановления сигнала достаточно знать его в WT на некоторой довольно редкой решетке в фазовой плоскости (например, только в центре каждой ячейки на Фазовой плоскости WT
Идея преобразования - масштабировать вейвлет в некоторое постоянное (например, 2) число раз, и смещать его во времени на фиксированное расстояние, зависящее от масштаба. При этом все сдвиги одного масштаба должны быть попарно ортогональны – такие вейвлеты называются ортогональными. При таком преобразовании выполняется свертка сигнала с некоторой функцией (так называемой
скейлинг-функцией)
Слайд 4414 -14
Для входного сигнала, представленного массивом 2n чисел, вейвлет-преобразование (WT)
Хаара просто группирует элементы по 2 и образует от них
суммы и разности. Группировка сумм проводится рекурсивно (в случае чётной длины последовательности сумм) для образования следующего уровня разложения. В итоге получается 2n−1 разность и 1 общая сумма..
wavelet означает маленькая волна WT А. Хаар
Термин вейвлет-анализ по смыслу аналогичен термину Фурье-анализ. В обоих случаях речь идет о представлении исследуемого процесса в виде линейной комбинации различных функций, именуемых базисом соответствующего преобразования.
Слайд 4514 -1
Слово вейвлет означает маленькая волна. Под маленькой понимается то,
что эта функция (окно) имеет конечную ширину (компактный носитель). Слово
«волна» отражает тот факт, что вейвлет-функция осциллирует.
Термин «материнский» означает, что функции с различной шириной носителя, используемые в преобразовании, порождаются одной базовой функцией - материнским вейвлетом. То есть материнский вейвлет является прототипом для всех оконных функций.
Термин сдвиг используется здесь в том же смысле, что и при ПФ: он относится к местоположению окна, и окно движется вдоль сигнала. Этот термин относится, таким образом, к временной информации, присутствующей в результате преобразования.
В случае WT мы не имеем частотного параметра, как это было при ОПФ. Вместо него здесь имеется параметр масштаба, который можно определить как величину, обратную частоте.
Слайд 4614 -15
Для преобразования Фурье базисом являются функции Wn(t), полученные из
функции FT
Ψn(t) = Ψ(nt).
w(t) имеет период 2π.
FT
широко используется для спектрального анализа
сигналов, однако имеет ряд недостатков
а) исходный сигнал заменяется на периодический, с периодом равным длительности исследуемого образца,
б) FT плохо работает при изменении параметров процесса со временем (нестационарности), поскольку дает усредненные коэффициенты для всего исследуемого образца
w(t) = e i t = cos t + i sin t,
FT WT
Слайд 4714 -1
Как для оконного Фурье преобразования (ОПФ) в случае непрерывного
(CFT) сигнал перемножается с функцией (вейвлетом), также как и с
оконной функцией при ОПФ, и преобразование выполняется раздельно для разных участков времени сигнала.
Однако существует две существенные разности между ОПФ и НВП (CFT) :
Ширина окна изменяется, так что преобразование вычисляется для каждой спектральной компоненты, что является наиболее важным свойством вейвлет-преобразования. ( в формуле a s, b τ)
Непрерывное вейвлет-преобразование определяется следующим образом Как видно из равенства, преобразованный сигнал есть функция двух переменных, tau и s, параметры сдвига и масштаба Слово вейвлет означает маленькая волна. Под маленькой понимается то, что эта функция (окно) имеет конечную ширину (компактный носитель).
Слово «волна» отражает тот факт, что вейвлет-функция осциллирует. Термин «материнский» означает, что функции с различной шириной носителя, используемые в преобразовании, порождаются одной базовой функцией - материнским вейвлетом.
Масштаб определяется как величина, обратную частоте.

Слайд 4814 -17
Вейвлет-преобразование (WT) в большой степени позволяет преодолеть перечисленные недостатки
FT, поскольку базисные функции WT обладают свойством временной локализации,
обладают
конечной энергией (нормой):
Часто используемые вейвлеты: (а)WAVE, (б)MHAT - мексиканская шляпа, (в) Morlet - Морле, (г)Paul - Пауля, (д) LMB, (е)Daubechies - Добечи. Вейвлеты (в) и (г) являются комплексными.
Временное представление некоторых вейвлетов и соответствующие им Фурье-образы.
Слайд 4914 -18
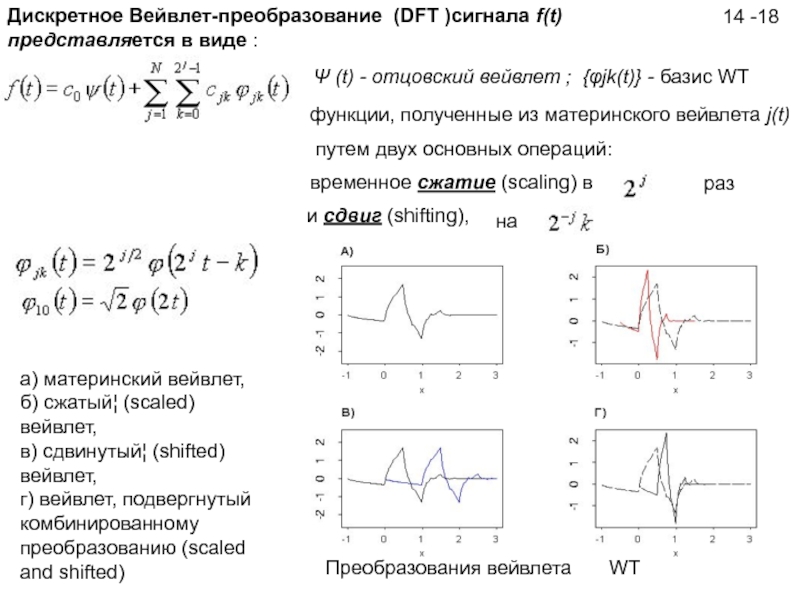
Дискретное Вейвлет-преобразование (DFT )сигнала f(t) представляется в виде :
функции,
полученные из материнского вейвлета j(t)
путем двух основных операций:
временное
сжатие (scaling) в
и сдвиг (shifting),
раз
на
Преобразования вейвлета
WT
Ψ (t) - отцовский вейвлет ; {φjk(t)} - базис WT
а) материнский вейвлет,
б) сжатый¦ (scaled) вейвлет,
в) сдвинутый¦ (shifted) вейвлет,
г) вейвлет, подвергнутый комбинированному преобразованию (scaled and shifted)
Слайд 5014 -19
Идея применения вейвлетов для многомасштабного анализа заключается в том,
что разложение сигнала производится по базису, образованному сдвигами и разномасштабными
копиями функции-прототипа
(то есть вейвлет-преобразование по своей сути является фрактальным).
Пример многомасштабного анализа изображения
Вычислительная процедура дискретного WT (DWT) состоит в вычислении временной свертки сигнала с {φjk(t)}
Длина вейвлета для каждого последующего масштаба уменьшается в 2 раза. Для DWT используется вычислительная процедура быстрого преобразования
Для масштаба j=1 определяется 2 коэффициента: c10 и c11 , для j=2 - 4 коэффициента и т.д., поэтому вычислительный алгоритм DWT называют пирамидальным алгоритмом.
Слайд 51Для удаления шума производят DWT, обрабатывают полученный образ и производят
обратное вейвлет-преобразование (IDWT). Алгоритм IDWT аналогичен алгоритму DWT
Необходимым условием для
возможности осуществить восстановление сигнала по его DWT путем обратного преобразования является ортогональность базиса. К ортогональным относится базис на основе вейвлета Добечи.
ОТОБРАЖЕНИЕ ПРЕОБРАЗОВАНИЯ
Результатом вейвлет-преобразования одномерного числового ряда (сигнала) является двумерный массив значений коэффициентов С(a,b). Распределение этих значений в пространстве (a,b) - временной масштаб, временная локализация, дает информацию об изменении во времени относительного вклада в сигнале вейвлетных компонент разного масштаба и называется спектром коэффициентов вейвлет-преобразования, масштабно-временным (частотно-временным) спектром или просто вейвлет-спектром (wavelet spectrum). Спектр C(a,b) одномерного сигнала представляет собой поверхность в трехмерном пространстве.
Способы визуализации спектра могут быть самыми различными
Слайд 52Отображение преобразования
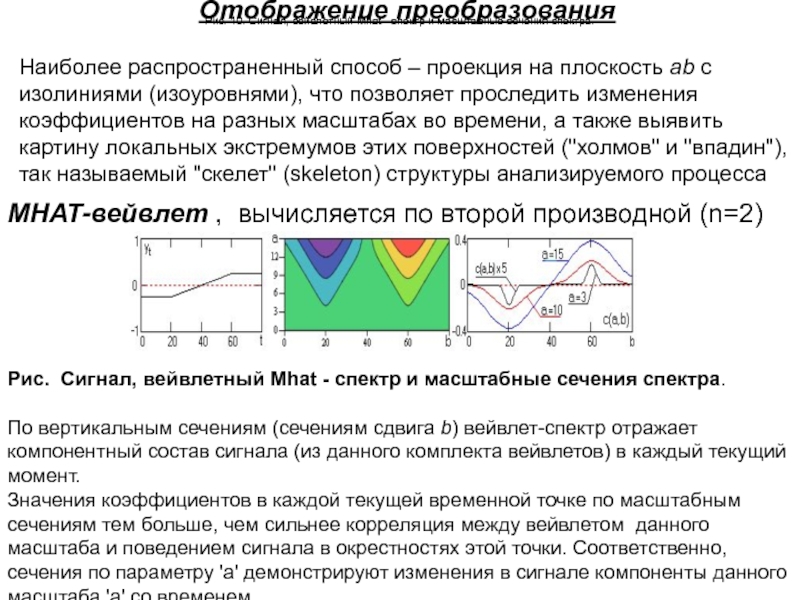
Наиболее распространенный способ – проекция на плоскость ab с
изолиниями (изоуровнями), что позволяет проследить изменения коэффициентов на разных масштабах
во времени, а также выявить картину локальных экстремумов этих поверхностей ("холмов" и "впадин"), так называемый "скелет" (skeleton) структуры анализируемого процесса
Рис. 10. Сигнал, вейвлетный Mhat - спектр и масштабные сечения спектра.
Рис. 10. Сигнал, вейвлетный Mhat - спектр и масштабные сечения спектра.
Рис. Сигнал, вейвлетный Mhat - спектр и масштабные сечения спектра.
По вертикальным сечениям (сечениям сдвига b) вейвлет-спектр отражает компонентный состав сигнала (из данного комплекта вейвлетов) в каждый текущий момент.
Значения коэффициентов в каждой текущей временной точке по масштабным сечениям тем больше, чем сильнее корреляция между вейвлетом данного масштаба и поведением сигнала в окрестностях этой точки. Соответственно, сечения по параметру 'а' демонстрируют изменения в сигнале компоненты данного масштаба 'a' со временем.
МНАТ-вейвлет , вычисляется по второй производной (n=2)
Слайд 53:
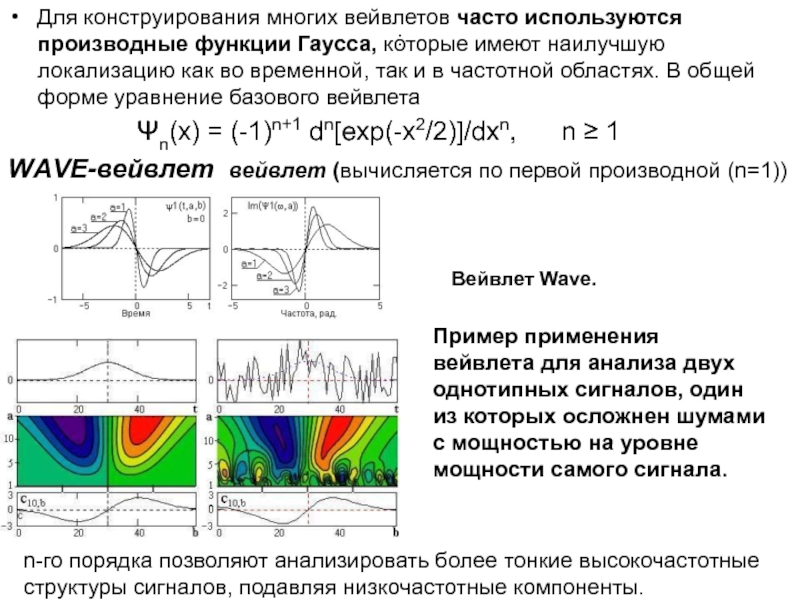
Для конструирования многих вейвлетов часто используются производные функции Гаусса,
которые имеют наилучшую локализацию как во временной, так и в
частотной областях. В общей форме уравнение базового вейвлета
Ψn(x) = (-1)n+1 dn[exp(-x2/2)]/dxn, n ≥ 1
WАVE-вейвлет вейвлет (вычисляется по первой производной (n=1))
Вейвлет Wave.
Пример применения вейвлета для анализа двух однотипных сигналов, один из которых осложнен шумами с мощностью на уровне мощности самого сигнала.
n-го порядка позволяют анализировать более тонкие высокочастотные структуры сигналов, подавляя низкочастотные компоненты.
Слайд 54
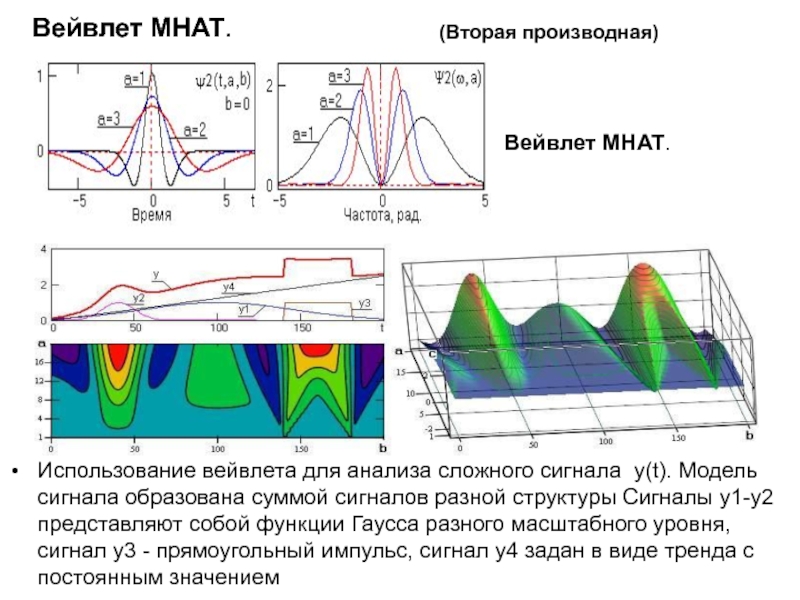
Использование вейвлета для анализа сложного сигнала y(t). Модель сигнала образована
суммой сигналов разной структуры Сигналы y1-y2 представляют собой функции Гаусса
разного масштабного уровня, сигнал y3 - прямоугольный импульс, сигнал y4 задан в виде тренда с постоянным значением
Вейвлет MHAT.
(Вторая производная)
Вейвлет MHAT.
Слайд 55 Свойства вейвлет-преобразования
Получение объективной информации о сигнале базируется на свойствах
вейвлет-преобразования, общих для вейвлетов всех типов.
Свойства WT
* Линейность TW[a·s1(t)+b·s2(t)]
= a·TW[s1(t)]+b·TW[s2(t)].
TW векторной функции есть вектор с компонентами TW
каждой из компонент анализируемого вектора в отдельности
*Инвариантность относительно сдвига
Сдвиг сигнала во времени на t0 приводит к сдвигу вейвлет-спектра также на t0: TW[s(t-to)] = C(a, b-to).
*Инвариантность относительно масштабирования
TW[s(t/аo)] = (1/ао)·C(a/ао,b/аo).
*Дифференцирование
dn{TW[s(t)]}/dtn = TW[dn(s(t))/dtn].
TW[dn(s(t))/dtn] = (-1)n s(t) [dn(y(t))/dtn] dt.
Слайд 56
Аналог теоремы Парсеваля для ортогональных и биортогональных вейвлетов
Сигнал может вычисляться
через коэффициенты вейвлет-преобразования.
s1(t)·s2*(t) = Cy-1 a-2 С(a,b) С*(a,b) da db
Вейвлет-преобразование простых сигналов.
Вейвлет-преобразование, выполняемое при анализе сигналов для выявления в них каких-либо особенностей и места их локализации без обратной реконструкции, допускает применение любых типов вейвлетов, как ортогональных, так и неортогональных.
Чаще всего для этих целей используются симметричные вейвлеты.
Результаты применения вейвлета Mhat для анализа сигналов простых форм. Вычисления выполнены с вейвлетом
(по формуле): с(a,b) = s(t) Ψ(t,a,b), с шагом Δt = Δb = Δa = 1.
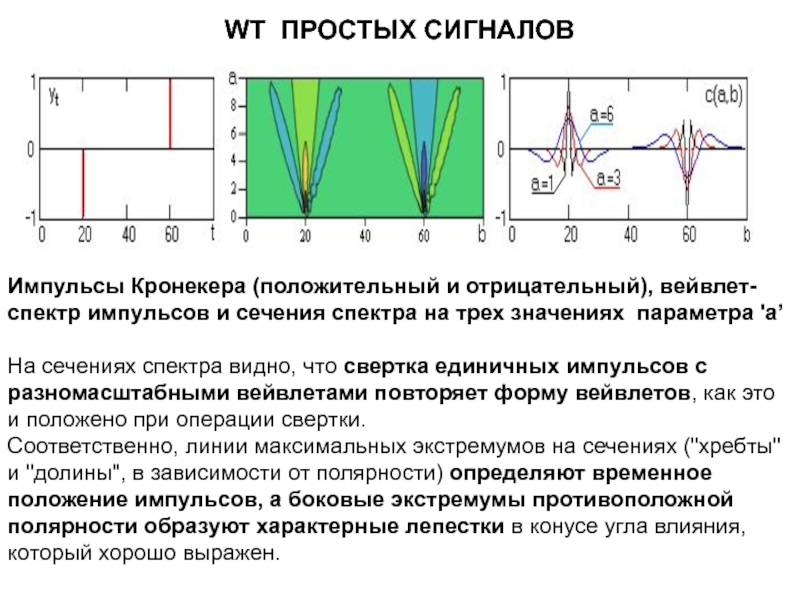
Слайд 57WT ПРОСТЫХ СИГНАЛОВ
Импульсы Кронекера (положительный и отрицательный), вейвлет-спектр импульсов и
сечения спектра на трех значениях параметра 'а’
На сечениях спектра видно,
что свертка единичных импульсов с разномасштабными вейвлетами повторяет форму вейвлетов, как это и положено при операции свертки.
Соответственно, линии максимальных экстремумов на сечениях ("хребты" и "долины", в зависимости от полярности) определяют временное положение импульсов, а боковые экстремумы противоположной полярности образуют характерные лепестки в конусе угла влияния, который хорошо выражен.
Слайд 58
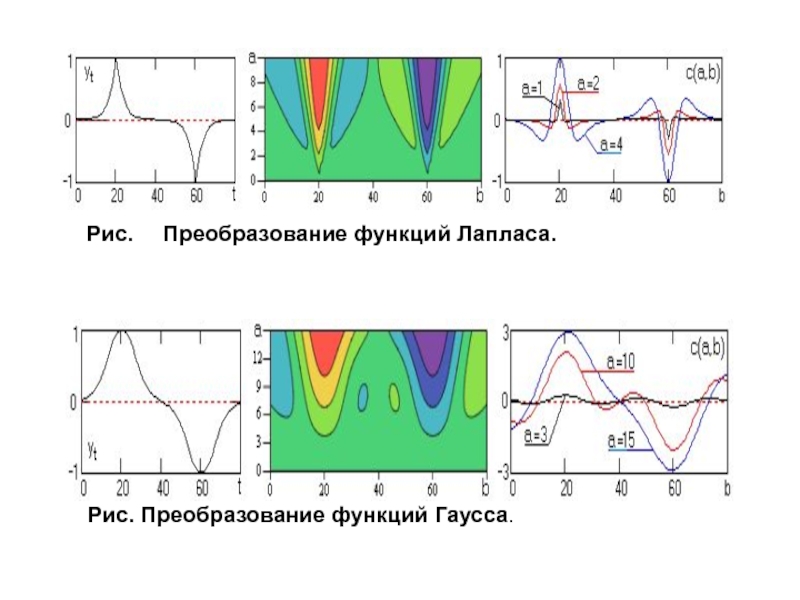
Рис. Преобразование функций Лапласа.
Рис. Преобразование
функций Гаусса.
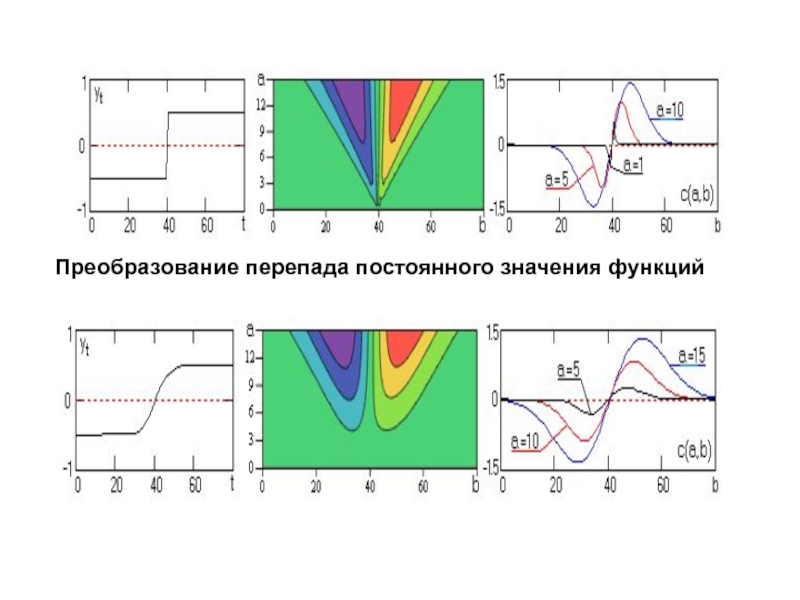
Слайд 59Преобразование перепада постоянного значения функций
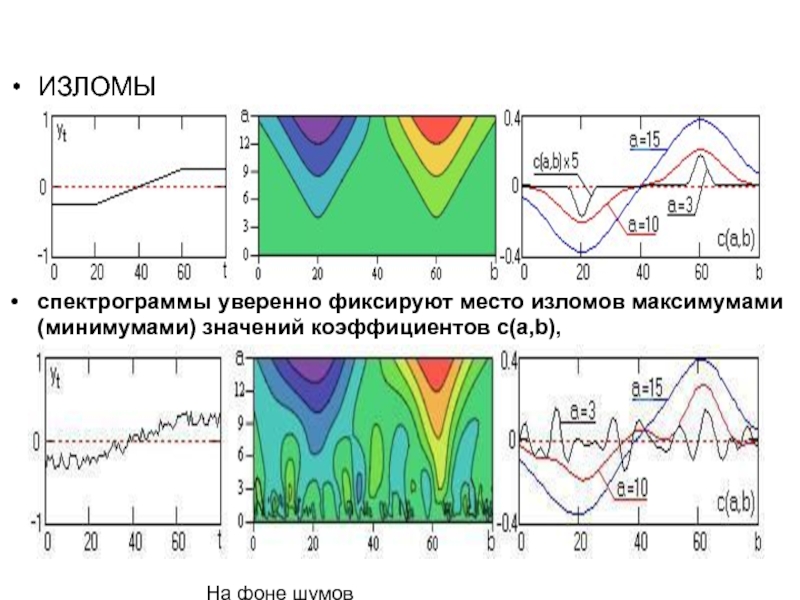
Слайд 60ИЗЛОМЫ
спектрограммы уверенно фиксируют место изломов максимумами (минимумами) значений коэффициентов c(a,b),
На фоне шумов
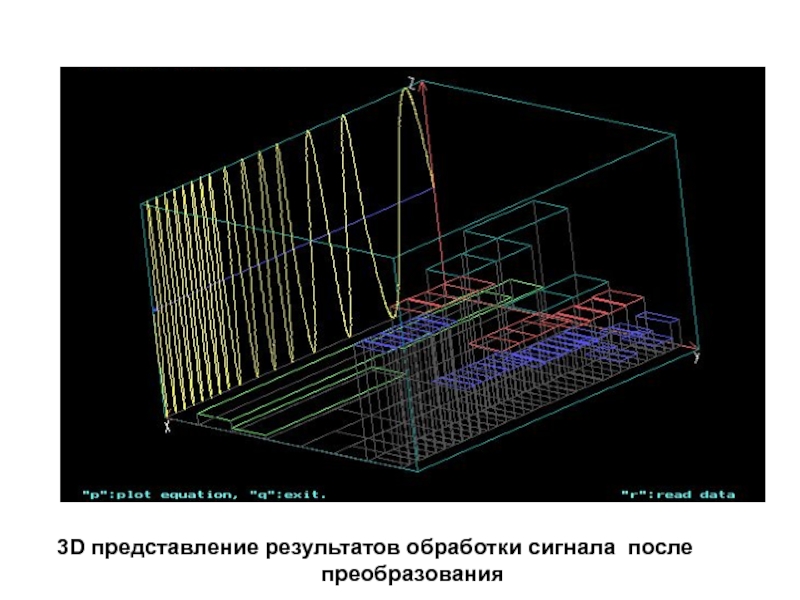
Слайд 61 3D представление результатов обработки сигнала после
преобразования
Слайд 6214 -20
Обработка экспериментальных данных. Вейвлет-преобразование дает наиболее наглядную и информативную
картину результатов эксперимента, позволяет очистить исходные данные от шумов и
случайных искажений, и даже "на глаз" подметить некоторые особенности данных и направление их дальнейшей обработки и анализа. Кроме того, вейвлеты хорошо подходят для анализа нестационарных сигналов, возникающих в медицине, анализе фондовых рынков и других областях
Обработка изображений. Используя вейвлет-преобразование, мы можем сгладить или выделить некоторые детали изображения, увеличить или уменьшить его, выделить важные детали и даже повысить его качество!
Сжатие данных. Особенностью ортогонального многомасштабного анализа является то, что для достаточно гладких данных полученные в результате преобразования детали в основном близки по величине к нулю и, следовательно, очень хорошо сжимаются обычными статистическими методами. Огромным достоинством вейвлет-преобразования является то, что оно не вносит дополнительной избыточности в исходные данные, и сигнал может быть полностью восстановлен с использованием тех же самых фильтров.
Области применения
WT

Слайд 63Фильтрацмя сигналов
DWT сигнала x получают применением набора фильтров. Сначала сигнал
пропускается через низкочастотный (low-pass) фильтр с импульсным откликом g, и
получается свёртка:
Одновременно сигнал раскладывается с помощью высокочастотного (high-pass) фильтра h. В результате получаются детализирующие коэффициенты (после ВЧ-фильтра) и коэффициенты аппроксимации (после НЧ-фильтра)
. Каждый из получившихся сигналов представляет половину частотной полосы исходного сигнала, так что частотное разрешение удвоилось.
Слайд 6414 -21
Кроме того, отделение в результате преобразования деталей от основного
сигнала позволяет очень просто реализовать сжатие с потерями – достаточно
просто отбросить детали на тех масштабах, где они несущественны!
Изображение, обработанное вейвлетами, можно сжать в 3-10 раз без существенных потерь информации (а с допустимыми потерями – до 300 раз!).
Вейвлет-преобразование положено в основу стандарта сжатия данных MPEG4.
а) DCT б)Оригинал в)DWT
Рис. Представление ДВП в частотной области
Слайд 6514 -1
Параметр масштаба в вейвлет-анализе имеет аналогию с масштабом географических
карт. Большие значения масштаба соответствуют малому количеству деталей, глобальному представлению
сигнала, а низкие значения масштаба позволяют различить детали. Аналогично, в терминах частоты, низкие частоты соответствуют глобальной информации о сигнале (которая содержится на всей его протяженности), а высокие частоты - детальной информации, скрытым особенностям, которые имеют обычно малую протяженность.
В определении вейвлет-преобразования коэффициент масштаба стоит в знаменателе. Поэтому, s > 1 расширяет сигнал, a s < 1 сжимает его.
Слайд 66Использованные источники
Астафьева Н.М. Вейвлет-анализ: Основы теории и примеры применения.
–
Успехи физических наук, 1996, т.166, № 11, стр. 1145-1170
2.
Добеши И. Десять лекций по вейвлетам. Москва, "РХД", 2001 г.
3. Дьяконов В., Абраменкова И. MATLAB. Обработка сигналов и изображений.
Специальный справочник. – СПб.: Питер, 2002, 608 с
4. Amara's Wavelet Page http://www.amara.com/current/wavelet.html
5. Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразования.
.-Петербург,
6. Mallat S. A theory for multiresolutional signal decomposition: the wavelet
representation. IEEE Trans. Pattern Analysis and Machine Intelligence, 1989,
N7, p.674-693
7. Max Fomitchev "An introduction to wavelets and wavelet transforms" http
://www.smolensk.ru/user/sgma/MMORPH/N-4-html/1.htm
8. WAVELETS Internet Sources http://www.cosy.sbg.ac.at/~uhl/wav.html
9. В.В. Геппенер, М.А. Соколов "Aдаптивные методы подавления мешающих
сигналов на основе wavelet-преобразования применительно к задачам
геолокации" http://inftech.webservis.ru
10. Широков И. Свойства вейвлет-преобразования
Частотно-временной анализ с использованием волнового преобразования
http://www.ecg.ru/pub/disser/pdima/disser/glava3_3_5.htm
8

Слайд 6714 -1
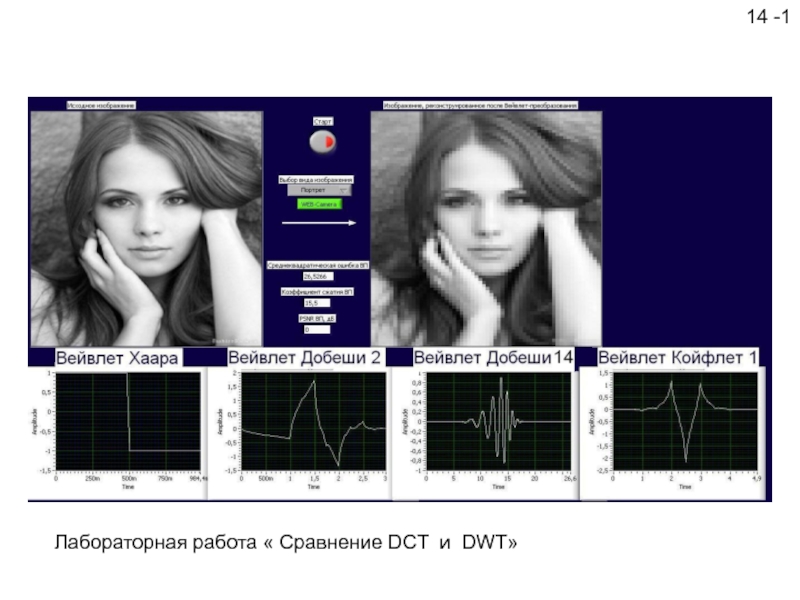
Лабораторная работа « Сравнение DCT и DWT»