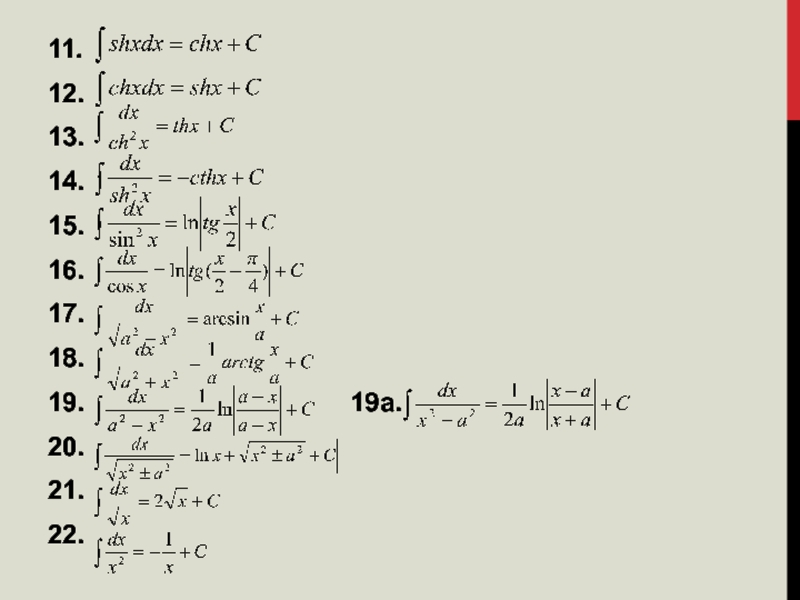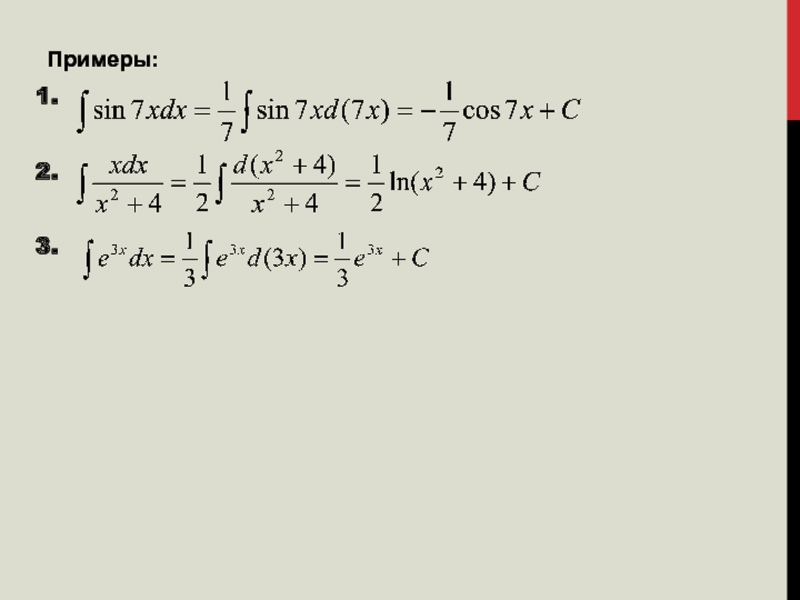Первообразная функция. Неопределенный интеграл

одной переменной является отыскание производной , или, иными словами, дифференцирование

данной функции .
К вопросу отыскание производной приводит ряд задач математики и её приложений к физики практике.
Например:
Решая задачу об отыскании скорости V, которую имеем в данный момент t точка, движущаяся по закону: мы сводим этот вопрос к отысканию производной: так что скорость v есть производная от пути до времени.
Но часто встречается необходимость в решении задачи, обратной задаче о дифференцировании функции.

функцию .
(это и есть основная задача интегрального исчисления)
К такой математической

задаче приводят многие физические, химические и другие задачи.
Например:
Задача о разыскании закона неравномерного движения материальной точки вдоль прямой по заданной скорости;
Задача о нахождении закона химической реакции по известной её скорости.

функции в этом промежутке , если для любого значения выполняется

равенство:
F'(x) = f(x)

- первообразная функции
в интервале

, поскольку для всех Х;

2) функция - первообразная функции
в интервале т.к.

3) функция - первообразная функции
, ибо .

первообразную.
Очевидно, далеко не всякая.
В дальнейшем (в разделе “Определённый интеграл”) нами

будет доказана следующая теорема:
Теорема. Любая, непрерывная на отрезке функция имеет на этом отрезке первообразную.
Далее возникает следующий вопрос:
Если некоторая функция имеет первообразную, то единственна ли эта первообразная?
Ответ и здесь будет отрицательным.

первообразной будет не только функция

, но и
, , и вообще всякая функция вида , где С – произвольная постоянная.
Функции такого вида исчерпывают все первообразные данной функции.
Справедлива следующая теорема, которая подтвердит это утверждение для любых функций.

, то

, где С - постоянная, так же является её первообразной.
Доказательство. 1)Если - первообразная функции, то . (1)
2)Но При заданной постоянной С функция также является первообразной функции f(x).
3)Покажем, что первообразных, не входящих в выражение , у функции быть уже не может.

, тогда

(2)
Из равенств (1) и (2) следует: , или
, см. следствие 2
Таким образом, выражение определяет
множество всех первообразных данной функции
в заданном промежутке .

называется множество всех её первообразных:

, где
Знак называется знаком неопределённого интеграла; функция подынтегральной функцией; выражение
- подынтегральным выражением; - переменная интегрирования.
Операция нахождения первообразной данной функции называется интегрирование.
Таким образом, чтобы найти неопределенный интеграл от данной функции , достаточно найти какую - либо её первообразную , и составить сумму , где С – произвольная постоянная.
Например. ,

равна под интегральной функции; дифференциал неопределённого интеграла равен подынтегральному выражению:

- по определению
2) -


2. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого:

Доказательство. Пусть .
.
По определению, Тогда

В частности, .

(к = const)

Доказательство. Сравним производные от обеих частей доказываемого равенства:
; .
Отсюда следует доказываемое равенства (при доказательстве учитывается, что неопределённый интеграл определён с точностью постоянного слагаемого).
Неопределённый интеграл от суммы нескольких слагаемых функции.
так, для 2-х слагаемых:
(*)

(*):

, т.е. для доказательства достаточно установить, что производные от обеих частей равны.
При вычислении неопределенных интегралов полезно знать следующее правило:
Если то . (1)
Дано, ;

правило (1) есть весьма частный случай замены переменной в неопределённом

интеграле).
Пример.
Проверка:

(Следовательно, равенство выполняется.)

более трудная, чем задача нахождения по данной функции её производной.
Для

некоторых часто встречающихся интегралов составлены таблицы.
Таблицу простейших неопределённых интегралов нетрудно получить, воспользовавшись тем, что интегрирование является операцией, обратной дифференцированию.
Будем исходить из следующего: если ,
то .
Например; поскольку то

следующую таблицу простейших неопределённых интегралов:

, ,

(а>0) 4а.

19а.
20.
21.
22.

тех промежутках, в которых определены соответствующие функции. Например, формула 3

справедлива для любого промежутка, не содержащего точку х=0, формула 9 – для интервала и т.п.

интегрирования получаются путем обращения формул для производных, поэтому перед изучением

настоящей темы необходимо повторить основные формулы дифференцирования функций.
Сравнивая операции дифференцирования и интегрирования функций, видим:
Если для дифференцируемости функции непрерывность функции является условием необходимым, но не достаточным, то для интегрируемости функции непрерывность функции на данном отрезке является только условием достаточным, но необходимым.
В то время как операция дифференцирования однозначна, операция интегрирования многозначна, ибо если функция имеет первообразную на отрезке, то она имеет и бесчисленное множество первообразных на этом отрезке.
Однако задача отыскания совокупности всех первообразных сводится к задаче отыскания только одной первообразной, так как все первообразные данной функции отличаются друг от друга на постоянное слагаемое.

опирается на:
таблицу интегралов;
основные свойства неопределенных интегралов.
Рассмотрим несколько примеров на применение

метода непосредственного интегрирования:
Пример 1. Найти неопределенный интеграл
I = (использовать свойства 4 и 3; формулы 2, 4а, 6 таблицы
простейших интегралов.) =

сумма производных постоянных есть также производная постоянная, которую и пишут

в конце.
Правильность выполненного интегрирования проверяется дифференцированием полученного результата, которое должно дать под интегральную функцию.
Проверка:

Пример 2.


Пример 3.

сложное на первый взгляд выражение, стоящее под знаком интеграла, удается

преобразовать и свести к простейшим формулам интегрирования:
Пример 5.


Замечание. В таблице основных интегралов предполагалось, что х является независимой переменной.

, где

- любая дифференцируемая функция новой переменной t.
Доказано, пусть (*) , , и пусть - дифференцируемая функция х.
В силу инвариантности формы первого дифференциала
, откуда
(**)

Итак, из справедливости формулы (*) следует справедливость формулы (**), которая получается из первой формулы формальной заменой х на U.
На основании этого свойства получаем обобщенную таблицу простейших интегралов.
и т.д.,
где u – любая дифференцируемая функция х.