Первообразная и интеграл

Содержание

1. Первообразная и интеграл
2. ПервообразнаяФункция F(x) называется первообразной для функции f(x)
3. Основное свойство первообразныхЕсли F(x) – первообразная функции
4. Неопределенный интегралСовокупность всех первообразных данной функции f(x)
5. Правила интегрирования
6. Определенный интегралВ декартовой прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми x=a, x=b (a
7. Определенный интегралВычислим площадь криволинейной трапеции. Разобьем отрезок
8. Связь между определенным интегралом и первообразной (Формула
9. Основные свойства определенного интеграла
10. Основные свойства определенного интеграла
11. Геометрический смысл определенного интегралаПлощадь криволинейной трапеции, ограниченной
12. Геометрический смысл определенного интегралаПлощадь криволинейной трапеции, ограниченной
13. Геометрический смысл определенного интегралаЗамечание: Если функция изменяет знак на промежутке [a;b] , то
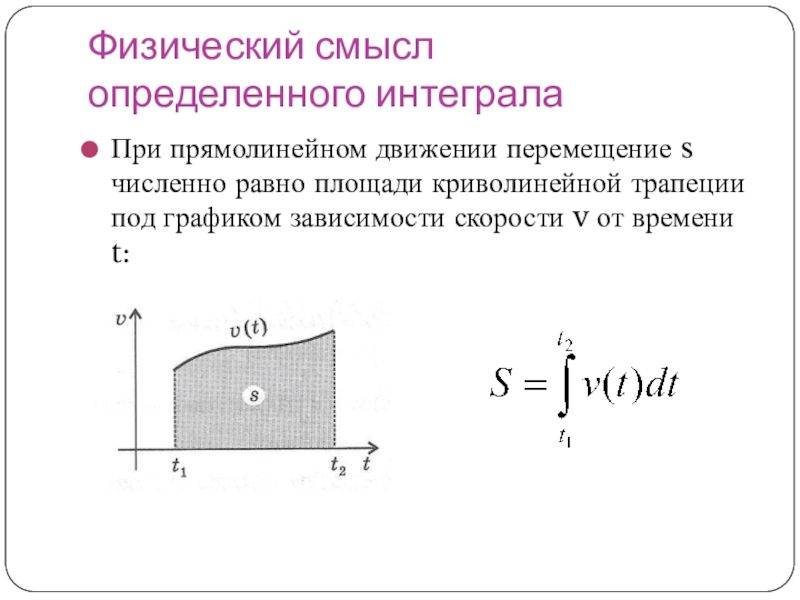
14. Физический смысл определенного интегралаПри прямолинейном движении перемещение
15. с помощью определенного интегралаВычисление площадей и объемов
16. Площадь фигуры,Ограниченной графиками непрерывных функций y=f(x) и
17. Объем тела,полученного в результате вращения вокруг оси
18. Скачать презентанцию

ПервообразнаяФункция F(x) называется первообразной для функции f(x) на данном промежутке, если для любого x из этого промежутка F’(x) = f(x).Пример: Первообразной для функции f(x)=x на всей числовой оси является F(x)=x2/2, поскольку (x2/2)’=x.

Главная
Разное
Первообразная и интеграл

Слайды и текст этой презентации

Слайд 1Учитель: Истлеупова А.А.
Первообразная и интеграл

Слайд 2Первообразная
Функция F(x) называется первообразной для функции f(x) на данном промежутке,

если для любого x из этого промежутка F’(x) = f(x).
Пример:
Первообразной

для функции f(x)=x на всей числовой оси является F(x)=x2/2, поскольку (x2/2)’=x.

ПервообразнаяФункция F(x) называется первообразной для функции f(x) на данном промежутке, если для любого x из этого промежутка

Слайд 3Основное свойство первообразных
Если F(x) – первообразная функции f(x), то и

функция F(x)+C, где C – произвольная постоянная, также является первообразной

функции f(x).

Графики всех первообразных данной функции f(x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси y.

Геометрическая интерпретация

Основное свойство первообразныхЕсли F(x) – первообразная функции f(x), то и функция F(x)+C, где C – произвольная постоянная,

Слайд 4Неопределенный интеграл
Совокупность всех первообразных данной функции f(x) называется ее неопределенным

интегралом и обозначается :

,

где C – произвольная постоянная.

Слайд 5Правила интегрирования

Слайд 6Определенный интеграл
В декартовой прямоугольной системе координат XOY фигура, ограниченная осью

OX, прямыми x=a, x=b (a

отрезке [a;b] функции y=f(x), называется криволинейной трапецией

Слайд 7Определенный интеграл
Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n

равных частей. Проведем через полученные точки прямые, параллельные оси OY.

Заданная криволинейная трапеция разобьется на n частей. Площадь всей трапеции приближенно равна сумме площадей столбиков.

по определению , его называют
определенным интегралом от функции
y=f(x) по отрезку [a;b] и обозначают так:

Определенный интегралВычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные точки прямые,

Слайд 8Связь между определенным интегралом и первообразной (Формула Ньютона - Лейбница)
Для непрерывной

функции

где F(x) – первообразная функции f(x).

Слайд 9Основные свойства определенного интеграла

Слайд 10Основные свойства определенного интеграла

Слайд 11Геометрический смысл определенного интеграла
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на

промежутке [a;b] функции f(x), осью x и прямыми x=a и

x=b:

Геометрический смысл определенного интегралаПлощадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x

Слайд 12Геометрический смысл определенного интеграла
Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на

промежутке [a;b] функции f(x), осью x и прямыми x=a и

x=b:

Геометрический смысл определенного интегралаПлощадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x), осью x

Слайд 13Геометрический смысл определенного интеграла
Замечание: Если функция изменяет знак на промежутке [a;b]

, то

Слайд 14Физический смысл определенного интеграла
При прямолинейном движении перемещение s численно равно площади

криволинейной трапеции под графиком зависимости скорости v от времени t:

Физический смысл определенного интегралаПри прямолинейном движении перемещение s численно равно площади криволинейной трапеции под графиком зависимости скорости

Слайд 15с помощью определенного интеграла
Вычисление площадей и объемов

Слайд 16Площадь фигуры,
Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что
для

любого x из [a;b], где a и b – абсциссы

точек пересечения графиков функций:

Площадь фигуры,Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b], где a и

Слайд 17Объем тела,
полученного в результате вращения вокруг оси x криволинейной трапеции,

ограниченной графиком непрерывной и неотрицательной функции y=f(x) на отрезке [a;b]:

Объем тела,полученного в результате вращения вокруг оси x криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной функции y=f(x)

Скачать презентацию

Разделы презентаций