Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Побудова епюр M, Q та N у балках та рамах. Визначення розмірів перерізу
Содержание
- 1. Побудова епюр M, Q та N у балках та рамах. Визначення розмірів перерізу
- 2. Для заданных балок, закрепленных и нагруженных как
- 3. Задача 1.2 м4 м1,5 мP =40 кНABCRD=24.533кН=24.533
- 4. zy2. Определяем значения поперечных сил и изгибающих
- 5. zy2 м4 м1,5 мP =40 кНABCRD=24.533кН=24.533 кНRAМ
- 6. zy2 м4 м1,5 мP =40 кНABCRD=24.533кН=24.533 кНRAМ
- 7. 3. Построение эпюр поперечных сил Qy и изгибающих моментов Mx .Qy, кНMx, кНм24,53324,53324,53324,533-+15,66715,667+49,067+25,06736,8+--
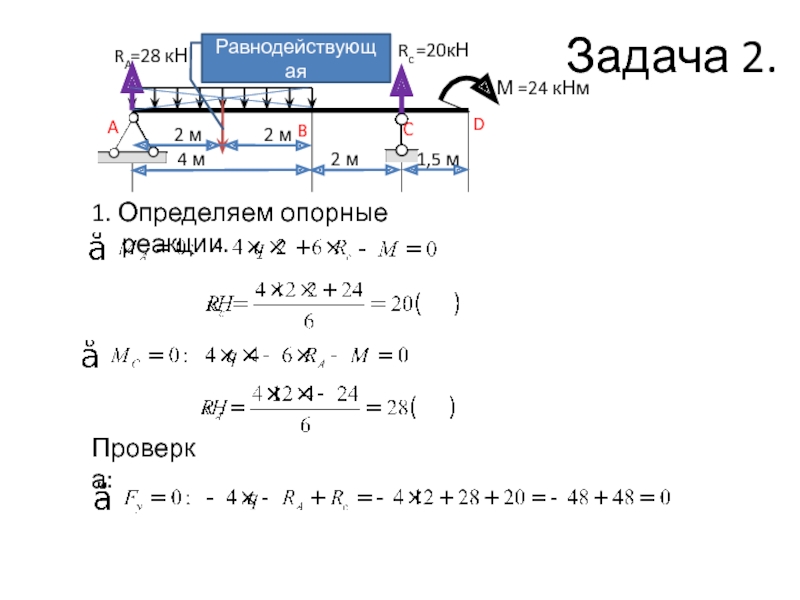
- 8. ABCDМ =24 кНмRc=20кН=28 кНRAq =12 кН/м2 м4 м1,5 м1. Определяем опорные реакции.Проверка:Равнодействующая2 м2 мЗадача 2.
- 9. 1z110 ≤ z1 ≤ 4мMx(z1) = RA∙z1
- 10. 1z2z112233z30 ≤ z2 ≤ 2мMx(z2) = RС∙z2
- 11. ABCDМ =24 кНмRc=20кН=28 кНRAq =12 кН/м2 м4
- 12. 2 м4 м1,5 мq =12 кН/мq =12 кН/мP =40 кНABCDRaRc1. Определяем опорные реакции.М =24 кНмПроверка:
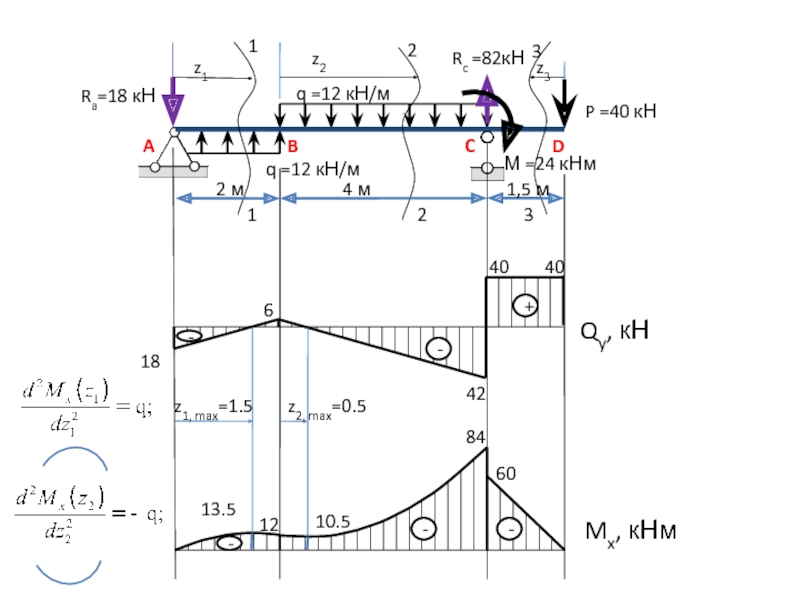
- 13. Балка имеет 3 участка: АВ, ВС, СD.1q
- 14. 1z2q =12 кН/мq =12 кН/мP =40 кНABCDRc=82кНz11220
- 15. 1z2z3q =12 кН/мq =12 кН/мP =40 кНABCDRc=82кНz1122330
- 16. 123Qy, кНMx, кНм1260186424040--+8413.510.5z1, max=1.5z2, max=0.5---М =24 кНм
- 17. Скачать презентанцию
Для заданных балок, закрепленных и нагруженных как показано на рисунке, требуется:определить опорные реакции;построить эпюры поперечных сил и изгибающих моментов, определив их значения во всех характерных точках, При этом для каждого участка
Слайды и текст этой презентации
Слайд 2Для заданных балок, закрепленных и нагруженных как показано на рисунке,
требуется:
определить опорные реакции;
построить эпюры поперечных сил и изгибающих моментов, определив
их значения во всех характерных точках, При этом для каждого участка записать аналитические выражения Мх и Qy с полным их исследованием.
Слайд 3Задача 1.
2 м
4 м
1,5 м
P =40 кН
A
B
C
RD
=24.533кН
=24.533 кН
RA
М =24 кНм
P
=40 кН
1. Определяем опорные реакции.
Проверка:
D
z
y
Рисуем расчетную схему, заданной балки.
HA
Слайд 4z
y
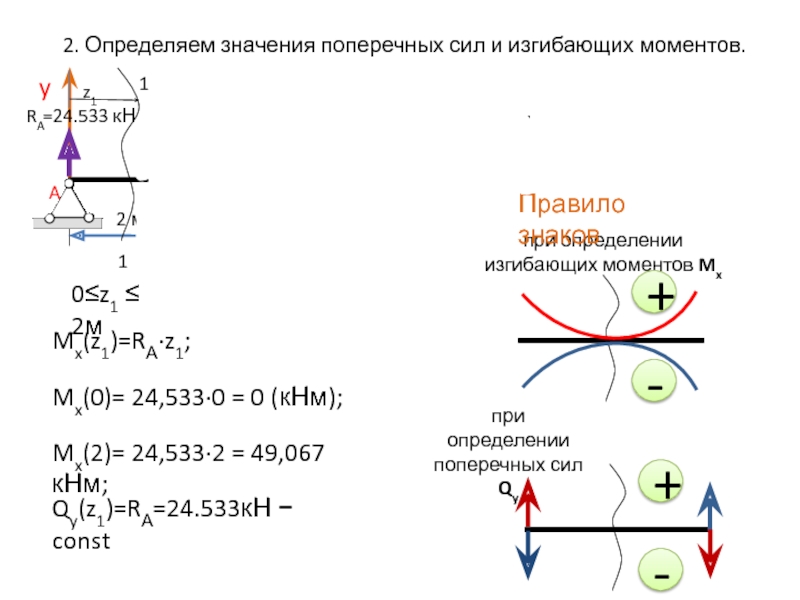
2. Определяем значения поперечных сил и изгибающих моментов.
2 м
4 м
1,5
м
P =40 кН
A
B
C
RD
=24.533кН
=24.533 кН
RA
М =24 кНм
P =40 кН
1
z1
1
D
0≤z1 ≤ 2м
Mx(z1)=RА∙z1;
Mx(0)=
24,533∙0 = 0 (кНм);Mx(2)= 24,533∙2 = 49,067кНм;
Qy(z1)=RА=24.533кН − const
при определении изгибающих моментов Mx
+
-
Правило знаков
при определении поперечных сил Qy
+
-
Слайд 5z
y
2 м
4 м
1,5 м
P =40 кН
A
B
C
RD
=24.533кН
=24.533 кН
RA
М =24 кНм
P =40
кН
z2
2
2
D
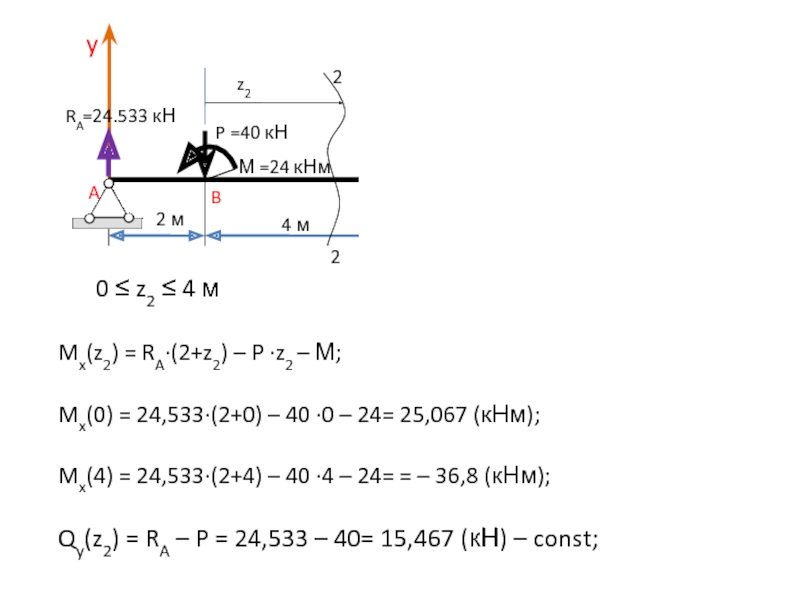
0 ≤ z2 ≤ 4 м
Mx(z2) = RA∙(2+z2) – P
∙z2 – М;Mx(0) = 24,533∙(2+0) – 40 ∙0 – 24= 25,067 (кНм);
Mx(4) = 24,533∙(2+4) – 40 ∙4 – 24= = – 36,8 (кНм);
Qy(z2) = RA – P = 24,533 – 40= 15,467 (кН) – const;
Слайд 6z
y
2 м
4 м
1,5 м
P =40 кН
A
B
C
RD
=24.533кН
=24.533 кН
RA
М =24 кНм
P =40
кН
1
z2
z3
z1
2
3
D
1
3
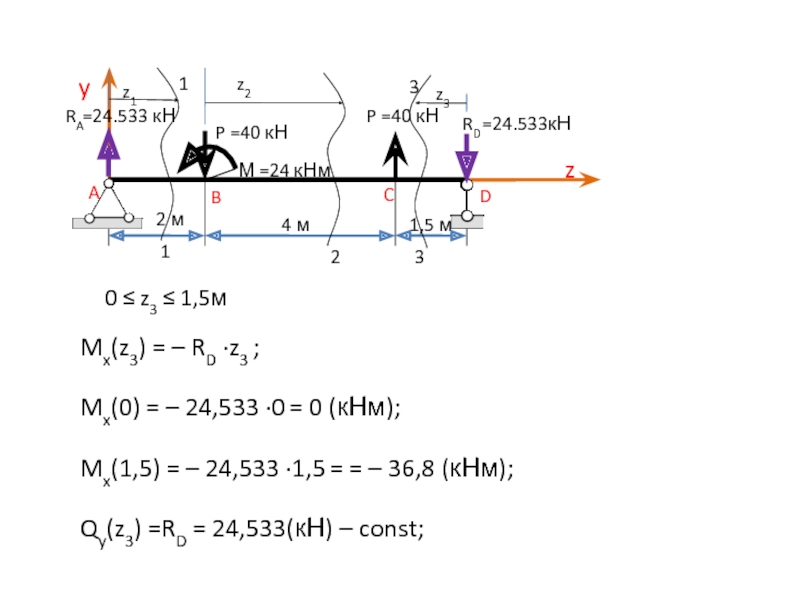
0 ≤ z3 ≤ 1,5м
Mx(z3) = – RD ∙z3 ;
Qy(z3)
=RD = 24,533(кН) – const;Mx(0) = – 24,533 ∙0 = 0 (кНм);
Mx(1,5) = – 24,533 ∙1,5 = = – 36,8 (кНм);
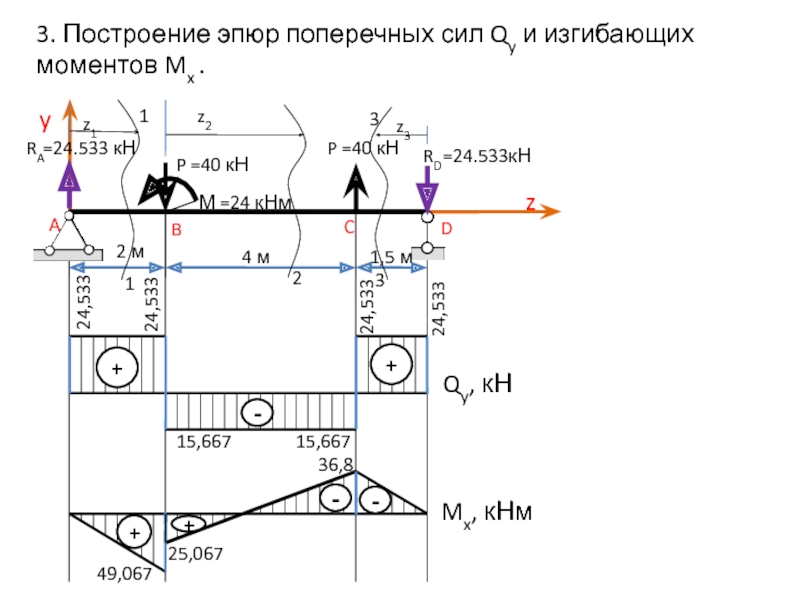
Слайд 73. Построение эпюр поперечных сил Qy и изгибающих моментов Mx
.
Qy, кН
Mx, кНм
24,533
24,533
24,533
24,533
-
+
15,667
15,667
+
49,067
+
25,067
36,8
+
-
-
Слайд 8A
B
C
D
М =24 кНм
Rc
=20кН
=28 кН
RA
q =12 кН/м
2 м
4 м
1,5 м
1. Определяем
опорные реакции.
Проверка:
Равнодействующая
2 м
2 м
Задача 2.
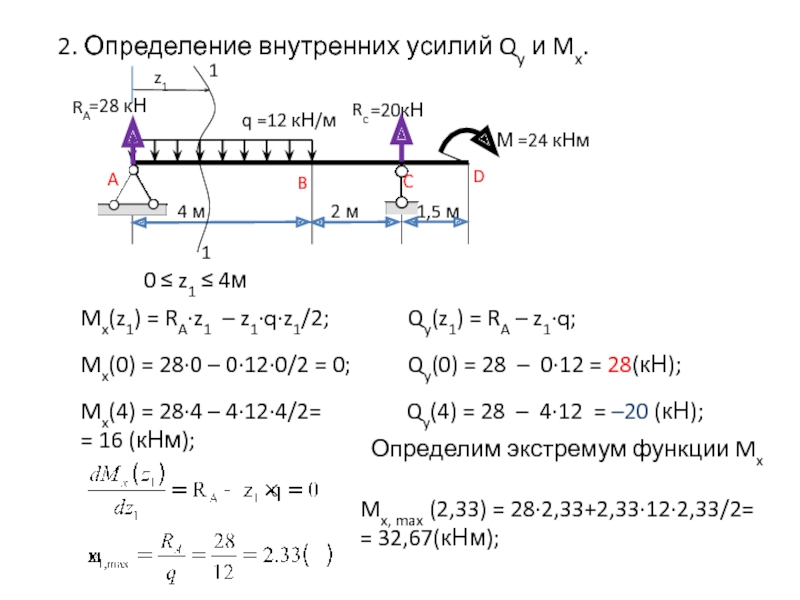
Слайд 91
z1
1
0 ≤ z1 ≤ 4м
Mx(z1) = RA∙z1 – z1∙q∙z1/2;
Mx(0) =
28∙0 – 0∙12∙0/2 = 0;
Mx(4) = 28∙4 – 4∙12∙4/2=
=
16 (кНм);Qy(z1) = RA – z1∙q;
Qy(0) = 28 – 0∙12 = 28(кН);
Qy(4) = 28 – 4∙12 = –20 (кН);
Mx, max (2,33) = 28∙2,33+2,33∙12∙2,33/2=
= 32,67(кНм);
2. Определение внутренних усилий Qy и Mx.
Определим экстремум функции Mx
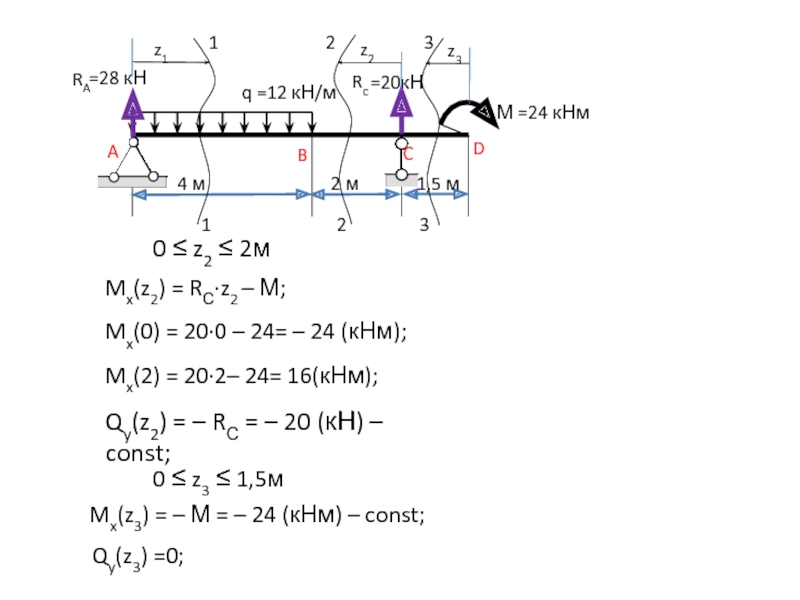
Слайд 101
z2
z1
1
2
2
3
3
z3
0 ≤ z2 ≤ 2м
Mx(z2) = RС∙z2 – М;
Mx(0) =
20∙0 – 24= – 24 (кНм);
Mx(2) = 20∙2– 24= 16(кНм);
Qy(z2)
= – RС = – 20 (кН) – const;0 ≤ z3 ≤ 1,5м
Mx(z3) = – М = – 24 (кНм) – const;
Qy(z3) =0;
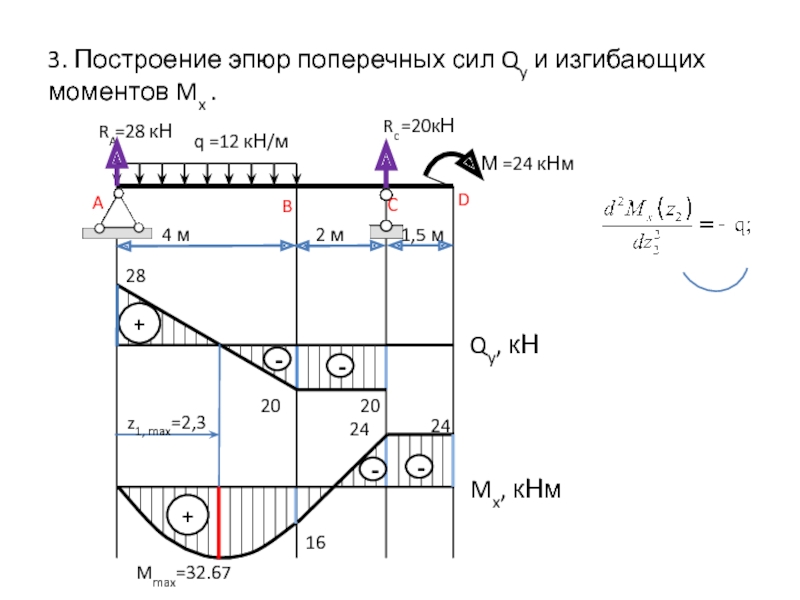
Слайд 11A
B
C
D
М =24 кНм
Rc
=20кН
=28 кН
RA
q =12 кН/м
2 м
4 м
1,5 м
3. Построение
эпюр поперечных сил Qy и изгибающих моментов Mx .
Qy, кН
Mx,
кНм20
28
-
+
20
-
16
z1, max=2,3
Mmax=32.67
+
24
-
24
-
Слайд 122 м
4 м
1,5 м
q =12 кН/м
q =12 кН/м
P =40 кН
A
B
C
D
Ra
Rc
1.
Определяем опорные реакции.
М =24 кНм
Проверка:
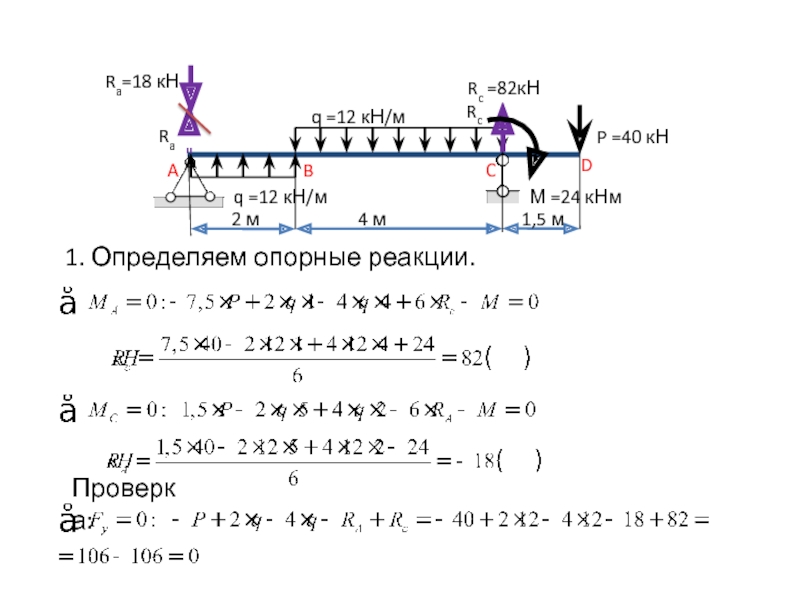
Слайд 13Балка имеет 3 участка: АВ, ВС, СD.
1
q =12 кН/м
q =12
кН/м
P =40 кН
A
B
C
D
Rc
=82кН
z1
1
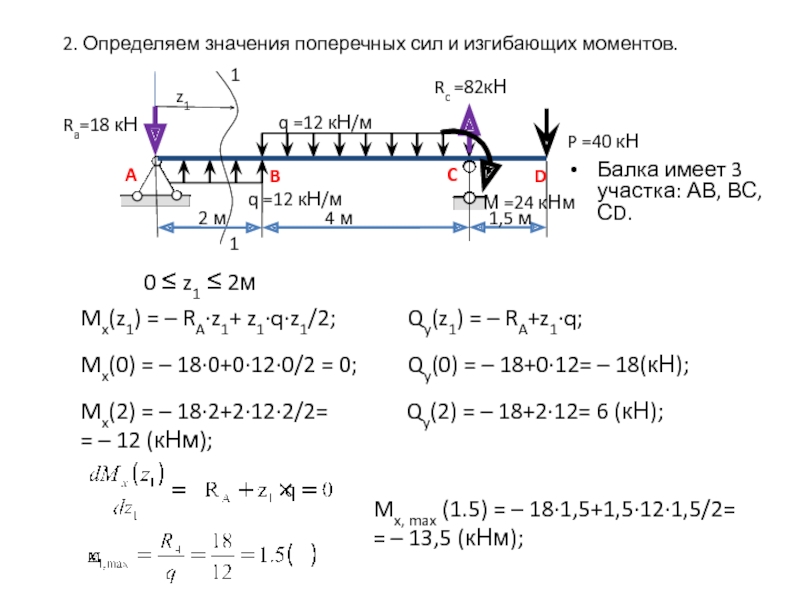
0 ≤ z1 ≤ 2м
Mx(z1) = – RA∙z1+
z1∙q∙z1/2;Mx(0) = – 18∙0+0∙12∙0/2 = 0;
Mx(2) = – 18∙2+2∙12∙2/2=
= – 12 (кНм);
Qy(z1) = – RA+z1∙q;
Qy(0) = – 18+0∙12= – 18(кН);
Qy(2) = – 18+2∙12= 6 (кН);
Mx, max (1.5) = – 18∙1,5+1,5∙12∙1,5/2=
= – 13,5 (кНм);
2. Определяем значения поперечных сил и изгибающих моментов.
М =24 кНм
Слайд 141
z2
q =12 кН/м
q =12 кН/м
P =40 кН
A
B
C
D
Rc
=82кН
z1
1
2
2
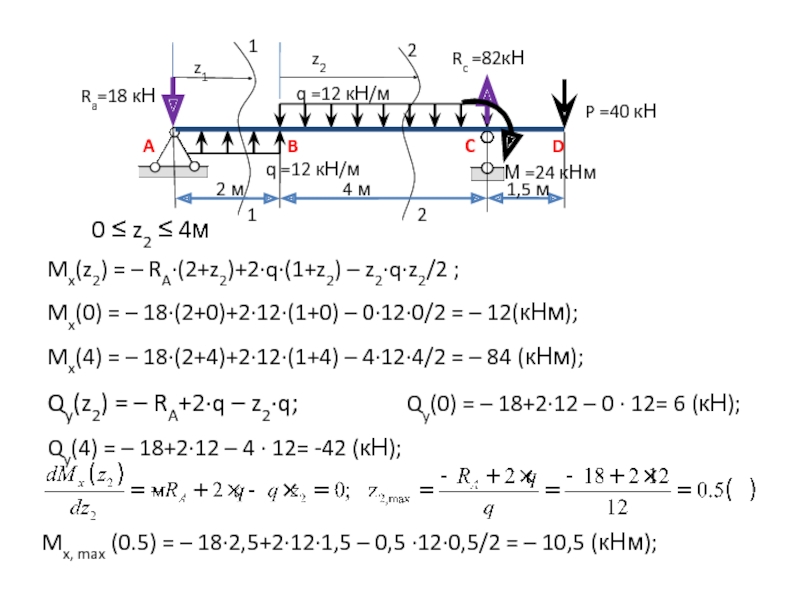
0 ≤ z2 ≤
4м
Mx(z2) = – RA∙(2+z2)+2∙q∙(1+z2) – z2∙q∙z2/2 ;
Mx(0) = – 18∙(2+0)+2∙12∙(1+0)
– 0∙12∙0/2 = – 12(кНм);Mx(4) = – 18∙(2+4)+2∙12∙(1+4) – 4∙12∙4/2 = – 84 (кНм);
Qy(z2) = – RA+2∙q – z2∙q;
Qy(0) = – 18+2∙12 – 0 ∙ 12= 6 (кН);
Qy(4) = – 18+2∙12 – 4 ∙ 12= -42 (кН);
Mx, max (0.5) = – 18∙2,5+2∙12∙1,5 – 0,5 ∙12∙0,5/2 = – 10,5 (кНм);
М =24 кНм
Слайд 151
z2
z3
q =12 кН/м
q =12 кН/м
P =40 кН
A
B
C
D
Rc
=82кН
z1
1
2
2
3
3
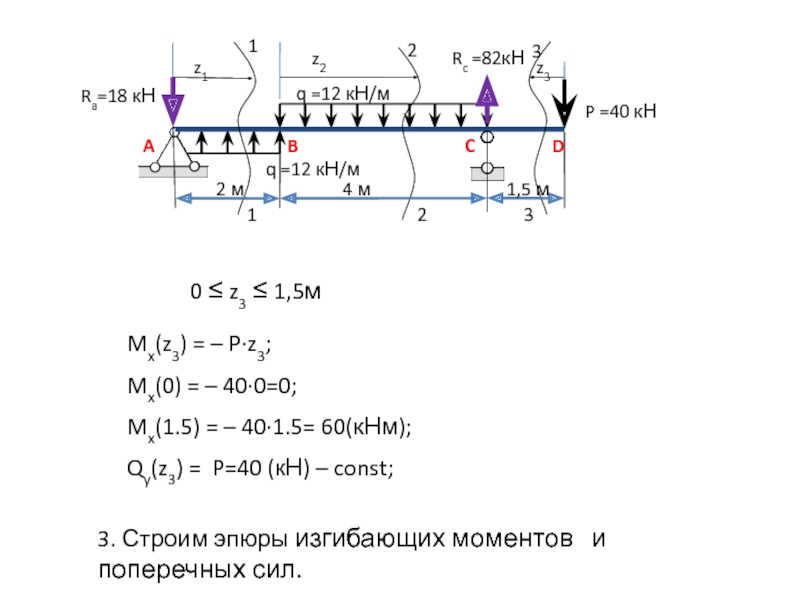
0 ≤ z3 ≤
1,5м
Mx(z3) = – P∙z3;
Mx(0) = – 40∙0=0;
Mx(1.5) = – 40∙1.5=
60(кНм);Qy(z3) = P=40 (кН) – const;
3. Строим эпюры изгибающих моментов и поперечных сил.
