показательной?
Показательной функцией называют функцию вида y=аx , где а>0, а≠1
2)
Какова область определения функции y=2x? x ∊ R 3) Какова область значения функции y=0,2x? y>0
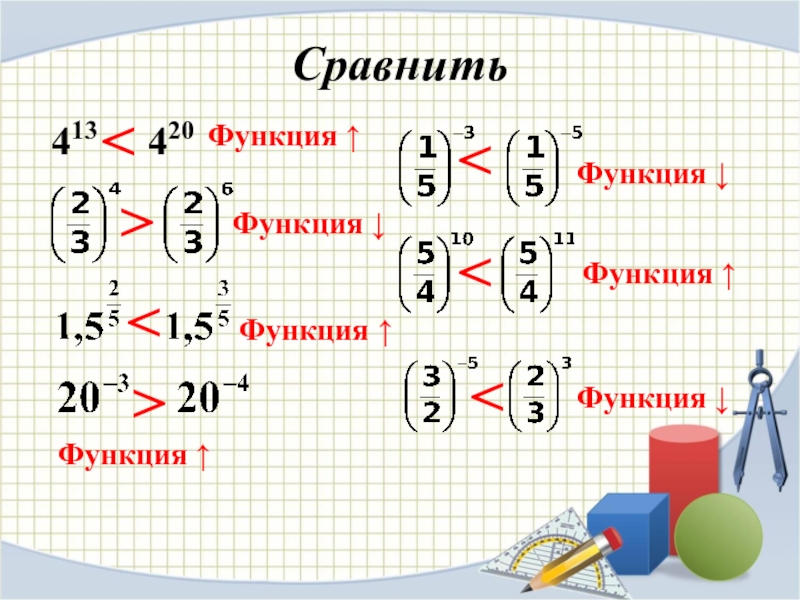
4) При каком условии показательная функция является возрастающей? a>1
5) При каком условии показательная функция является убывающей? a <1