Поверхности 2 порядка

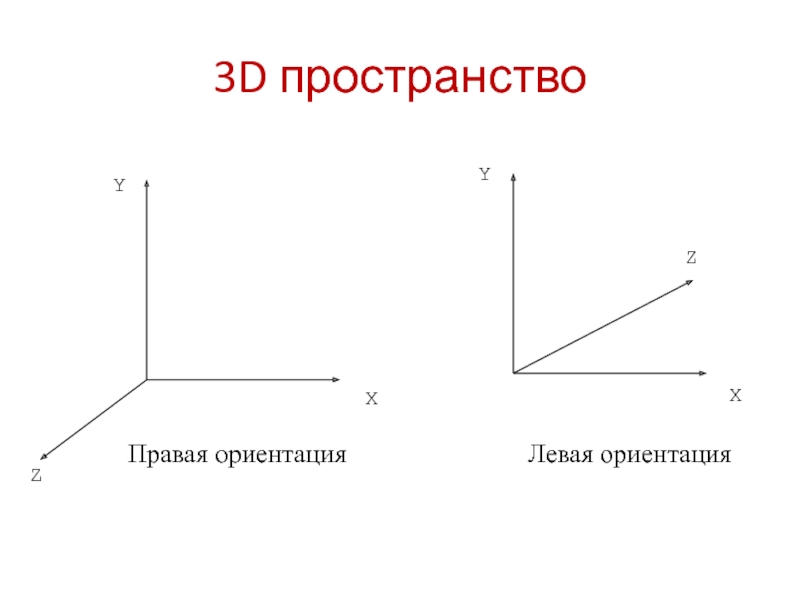
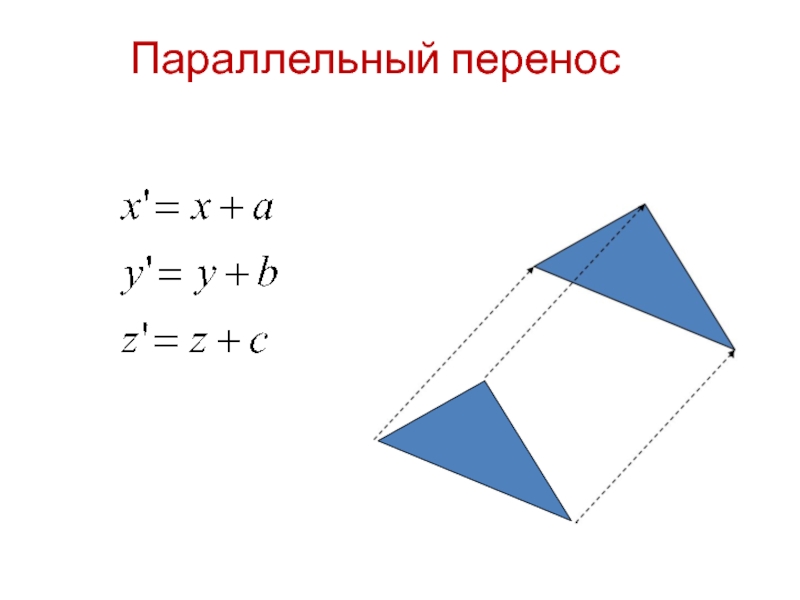
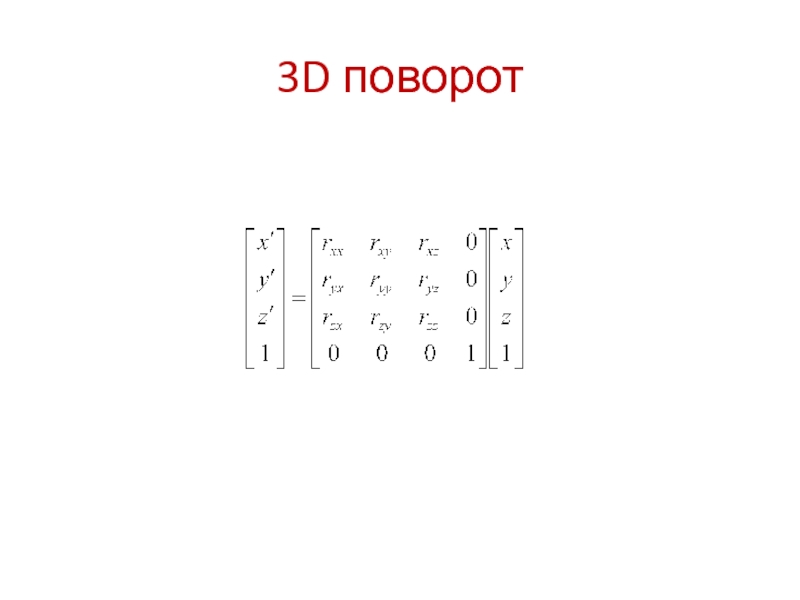
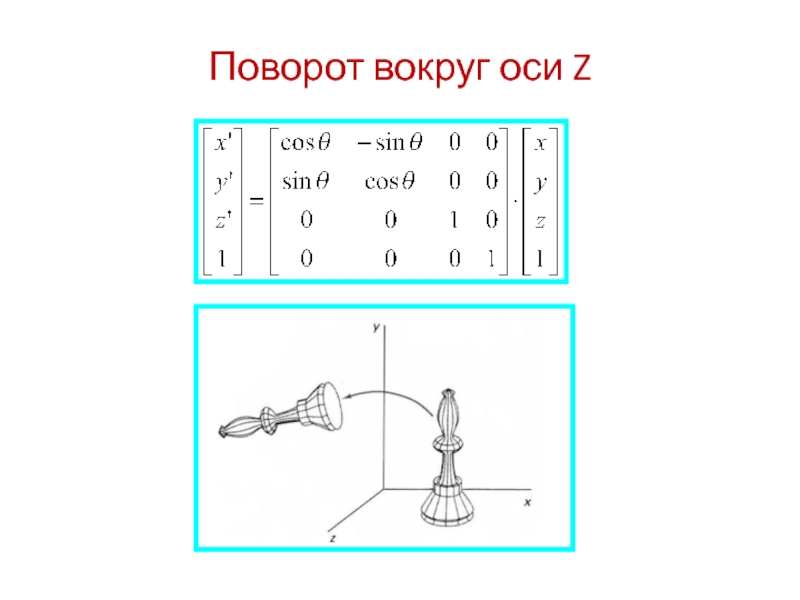
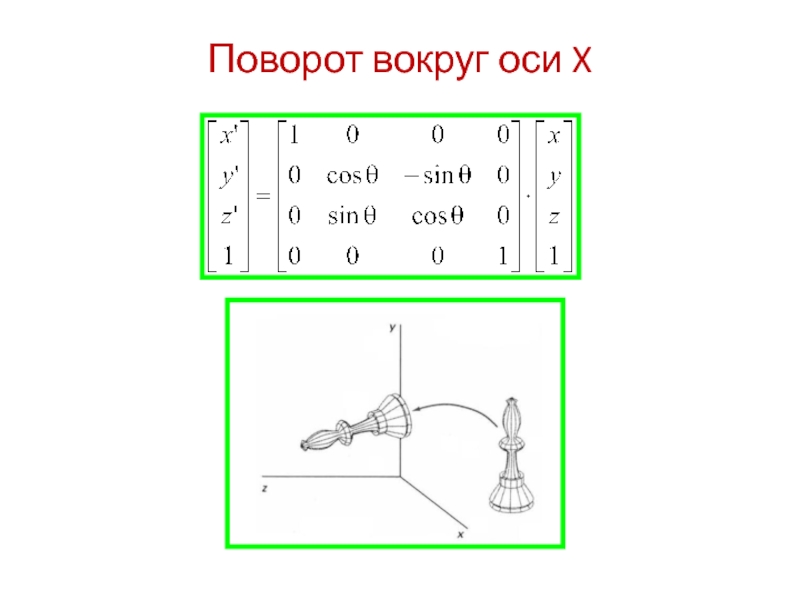
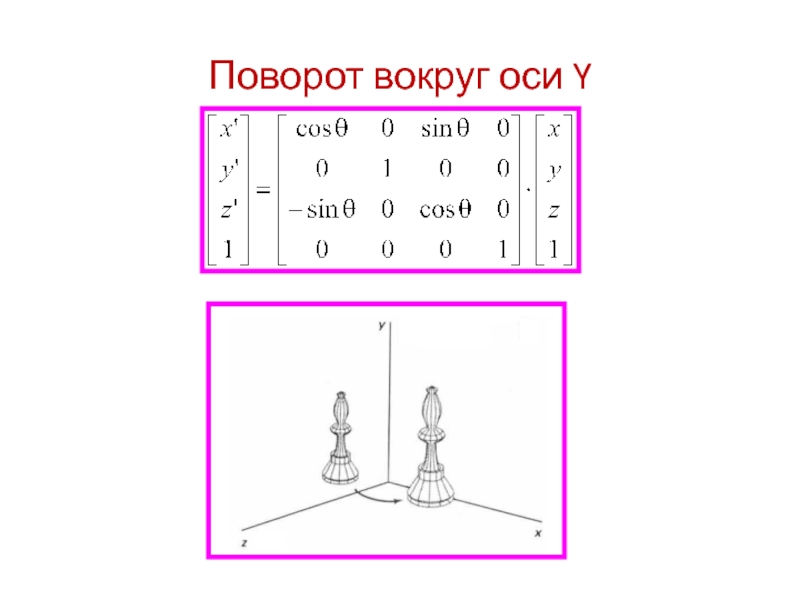
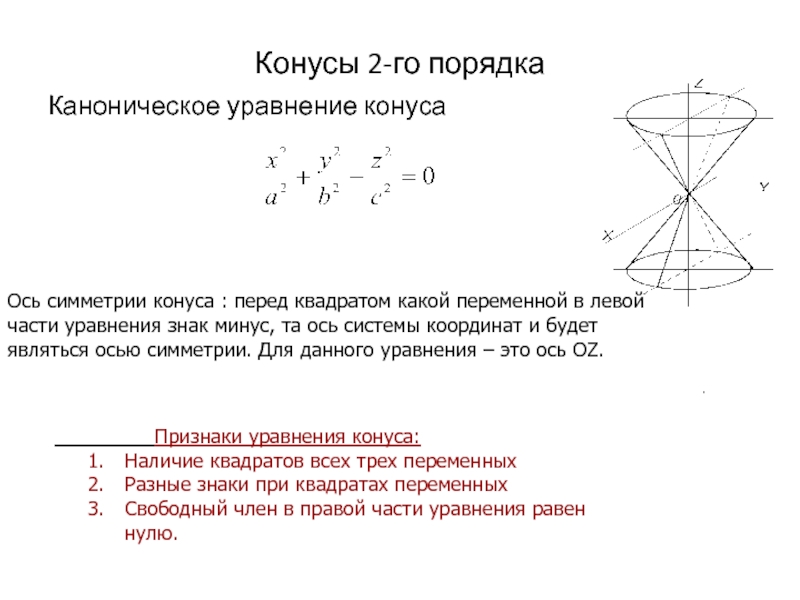
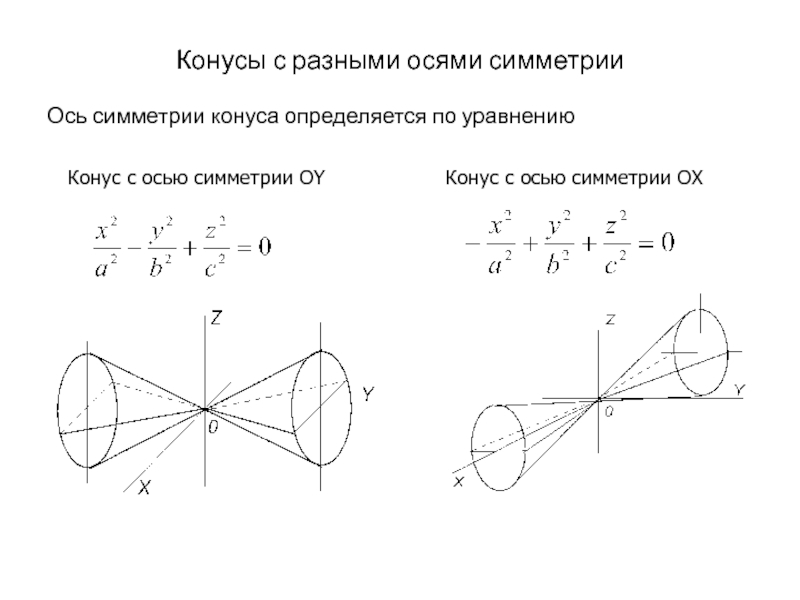
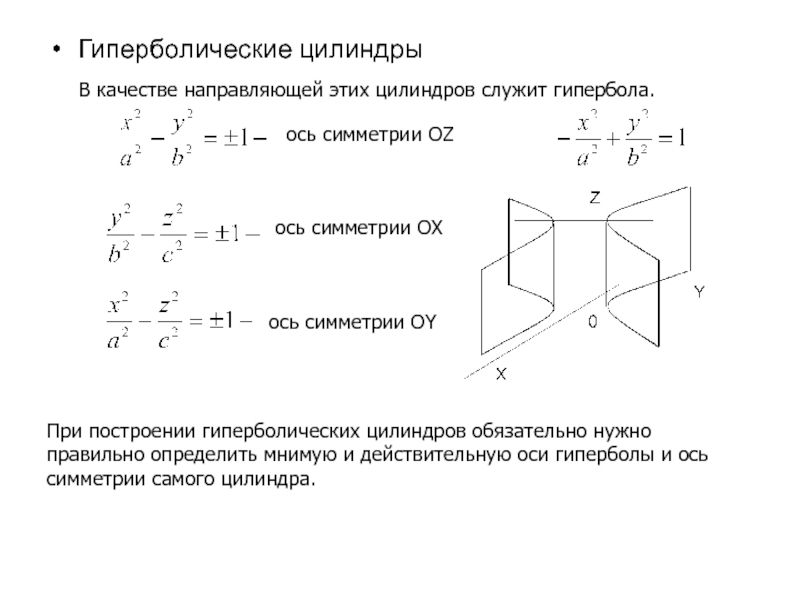
всякая ортогональная 3х3 матрица задает поворот:
Строки и столбцы образуют ортонормированную

линейная часть
.
Основная задача состоит в умении по уравнению определить

(поворот), приводящее главную часть к главным осям, так что преобразованное уравнение

Хотя бы один из коэффициентов при квадратах отличен от нуля, иначе матрица A была бы нулевой. Рассмотрим три случая.

параллельный перенос

получим

одинаковы

полуоси эллипсоида.
Центр этого эллипсоида находится
в начале координат.

Признаки уравнения эллипсоида:
Наличие

Признаки уравнения конуса:
Наличие квадратов всех трех переменных
Разные знаки

Ось симметрии конуса : перед квадратом какой переменной в левой части уравнения знак минус, та ось системы координат и будет являться осью симметрии. Для данного уравнения – это ось OZ.

с осью симметрии OY
Конус с осью симметрии OX

Признаки уравнения однополостного гиперболоида:
Наличие квадратов всех

полуоси

В зависимости от знака перед единицей в правой части гиперболоиды делятся на одно и двуполостные.

перед какой переменной в каноническом уравнении стоит знак минус.

Однополостный

Однополостный гиперболоид
с осью симметрии OX

Признаки уравнения двуполостного гиперболоида:
Наличие квадратов всех трех

полуоси

Если из уравнения выразить z, то получим

Т.к.

, то получается, что

Двуполостный гиперболоид на проходит через начало координат.

два знака минус в уравнении.
Один знак минус

).

Выделим полные квадраты


2.1.

).

2.1.1. с=0, знаки

).

2.1.3. ,

цилиндра строим эллипс с полуосями a и b в плоскости

Направляющей кривой являются эллипсы

).

2.1.4. с=0, знаки

цилиндров обязательно нужно
правильно определить мнимую и действительную оси гиперболы

В качестве направляющей этих цилиндров служит гипербола.

).

2.2.
Выделим полные квадраты


выполним параллельный перенос



получим

).

Преобразуем



Получим каноническое уравнение параболоида

отсутствует квадрат одной переменной.
В зависимости от знака между квадратами

Признаки уравнения эллиптического или кругового параболоида:
Отсутствие квадрата одной из переменных
Одинаковые знаки при квадратах переменных в левой части уравнения

Эллиптический
параболоид

параболоида:
Отсутствие квадрата одной из переменных
Разные знаки при квадратах переменных в

Отличительным признаком уравнения гиперболического параболоида
является то что в левой части уравнения между квадратами
переменных знак минус.

Эта поверхность имеет форму седла.

).

Выделим полный квадрат


выполним параллельный

).

3.1.

).
3.2. хотя бы один

симметрии OX
ось симметрии OY
ось симметрии OY
При построении цилиндра нужно определить

Направляющей этих цилиндров является парабола.