Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Представление информации в цифровых автоматах
Содержание
- 1. Представление информации в цифровых автоматах
- 2. Система счисления – совокупность приемов и правил
- 3. Древний Восток: (СС)12 вилки, ложки, тарелки;Английская система
- 4. Все системы счисления можно разделить на позиционные
- 5. Слайд 5
- 6. Слайд 6
- 7. Система счисления, в которой значение цифры определяется
- 8. (СС)10Алфавит – 0123456789, а основание р =
- 9. Слайд 9
- 10. Слайд 10
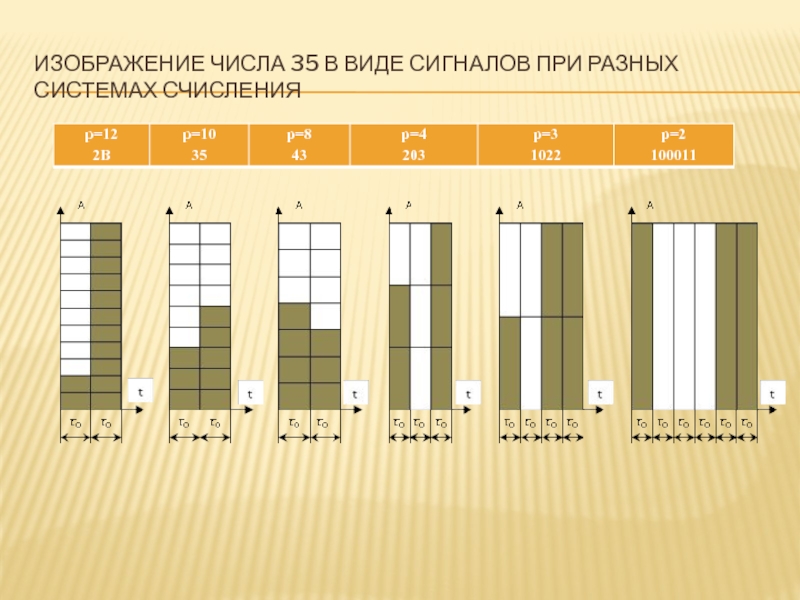
- 11. Например, десятичное число 35 в СС с основанием р=12,10,8,4,3,2 будет иметь вид:2В12 =2*121 +11*1203510=3*101+5*100438=4*81+3*802034=2*42+0*41+3*4010223=1*33+0*32+2*31+2*301000112=1*25+0*24+0*23+0*22+1*21+1*20
- 12. Из приведенных примеров видно, что с уменьшением
- 13. СС используются для построения на их основе
- 14. Слайд 14
- 15. Изображение числа 35 в виде сигналов при разных системах счисления
- 16. Анализ СС и построенных на их основе
- 17. Однако с ростом основания существенно повышаются требования
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Для перевода десятичного числа в двоичную систему
- 22. Для перевода десятичного числа в восьмеричную систему
- 23. Для перевода десятичного числа в шестнадцатеричную систему
- 24. Таблица 1. Наиболее важные системы счисления.
- 25. Чтобы перевести число из двоичной системы в
- 26. Чтобы перевести число из двоичной системы в
- 27. Для перевода восьмеричного числа в двоичное необходимо
- 28. При переходе из восьмеричной системы счисления в
- 29. Арифметические действия над числами в любой позиционной
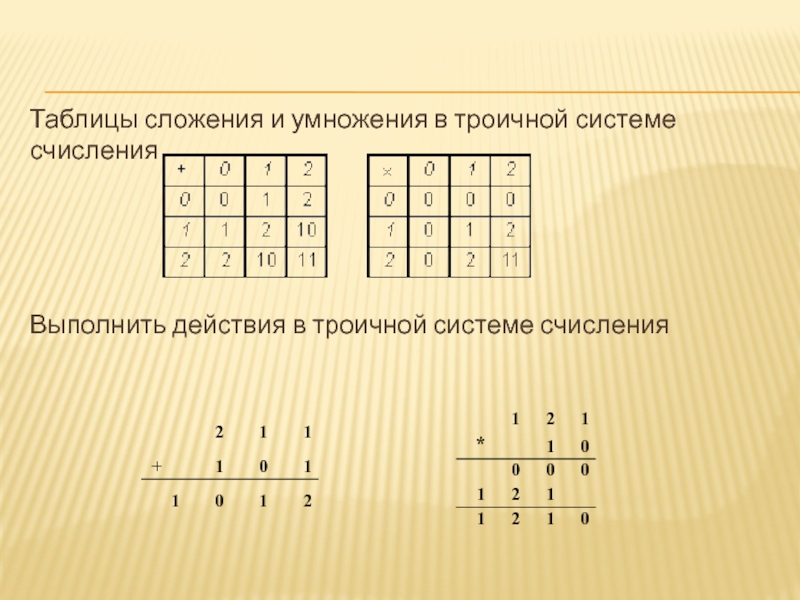
- 30. Таблицы сложения и умножения в троичной системе счисленияВыполнить действия в троичной системе счисления
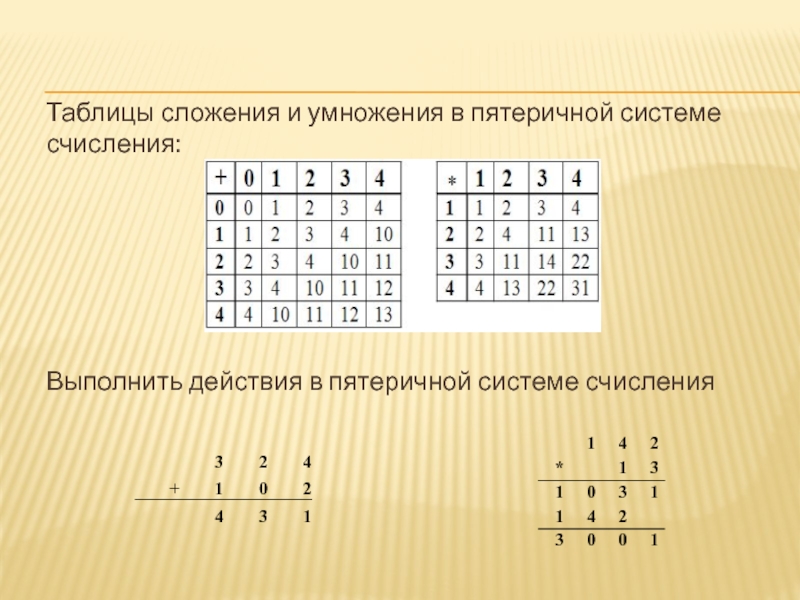
- 31. Таблицы сложения и умножения в пятеричной системе счисления: Выполнить действия в пятеричной системе счисления
- 32. Скачать презентанцию
Система счисления – совокупность приемов и правил наименования и обозначения чисел, позволяющих установить взаимно однозначное соответствие между любым числом и его представлением в виде конечного числа символов.В любой системе счисления выбирается
Слайды и текст этой презентации
Слайд 1Представление информации в цифровых автоматах
Системы счисления.
Позиционные и непозиционные СС.
Перевод
из одной СС в другую.
Слайд 2
Система счисления – совокупность приемов и правил наименования и обозначения
чисел, позволяющих установить взаимно однозначное соответствие между любым числом и
его представлением в виде конечного числа символов.В любой системе счисления выбирается алфавит, представляющий собой совокупность некоторых символов (или знаков).
Слайд 3Древний Восток: (СС)12
вилки, ложки, тарелки;
Английская система мер – 1
фут-12 дюймов;
1 шиллинг – 12 пенсов;
12 мес в году; дюжина.
Древний
Вавилон : (СС)601 час = 60м мин.
1 мин = 60 сек.
Слайд 4Все системы счисления можно разделить на позиционные и непозиционные.
Непозиционная система
счисления – система, в которой символы, обозначающие то или иное
количество, не меняют своего значения в зависимости от местоположения (позиции) в изображении числа.Слайд 7Система счисления, в которой значение цифры определяется местоположением (позицией) в
изображении числа, называется позиционной.
Упорядоченный набор символов (цифр) (a0, a1, …,
an), используемый для представления любых чисел в заданной позиционной СС, называют ее алфавитом, число символов (цифр) алфавита p=n+1 – ее основанием, а саму СС называют р-ричной.Основание позиционной СС – количество различных цифр, используемых для изображения чисел в данной СС.
Слайд 8(СС)10
Алфавит – 0123456789, а основание р = 10.
В 10-чной
СС каждый разряд имеет вес, равный степени 10. Следовательно, значение
одной и той же цифры определяется ее местоположением в изображении числа, характеризуемым степенью числа 10.Например:
222,22 = 2*102+2*101+2*100+2*10-1+2*10-2
Слайд 11 Например, десятичное число 35 в СС с основанием
р=12,10,8,4,3,2 будет иметь вид:
2В12 =2*121 +11*120
3510=3*101+5*100
438=4*81+3*80
2034=2*42+0*41+3*40
10223=1*33+0*32+2*31+2*30
1000112=1*25+0*24+0*23+0*22+1*21+1*20
Слайд 12Из приведенных примеров видно, что с уменьшением основания системы счисления
уменьшается число используемых цифр, но возрастает количество разрядов.
Все известные позиционные
СС являются аддитивно-мультипликативными. (числительные русского языка- 568 пять сотен плюс шесть десятков плюс восемь)
Слайд 13СС используются для построения на их основе различных кодов в
системах передачи, хранения и преобразования информации.
Код – система условных знаков
(символов ) для представления различной информации.Слайд 16Анализ СС и построенных на их основе кодов с позиций
применения в системах передачи, хранения и преобразования информации показывает, что
чем больше основание системы, тем меньше число разрядов требуется для представления данного числа, а следовательно и меньшее время для его передачи.Слайд 17Однако с ростом основания существенно повышаются требования к аппаратуре формирования
и распознавания элементарных сигналов, соответствующих различным символам. Логические элементы вычислительных
устройств в этом случае должны иметь большее число устойчивых состояний.С точки зрения минимальных затрат условного оборудования наиболее экономичной является СС с основанием 3.
Незначительно ей уступают ей двоичная и четверичная. СС с основанием 10 и более существенно менее эффективны.
Сравнивая эти системы с точки зрения удобства физической реализации соответствующих им логических элементов и простоты выполнения в них арифметических и логических действий, предпочтение в настоящее время отдается двоичной СС.
Действительно логические элементы, соответствующие этой СС должны иметь всего два устойчивых состояния. Задача различения сигналов сводится к задаче обнаружения (есть импульс или его нет), что значительно проще.
Арифметические и логические действия также легче осуществляются в двоичной системе.
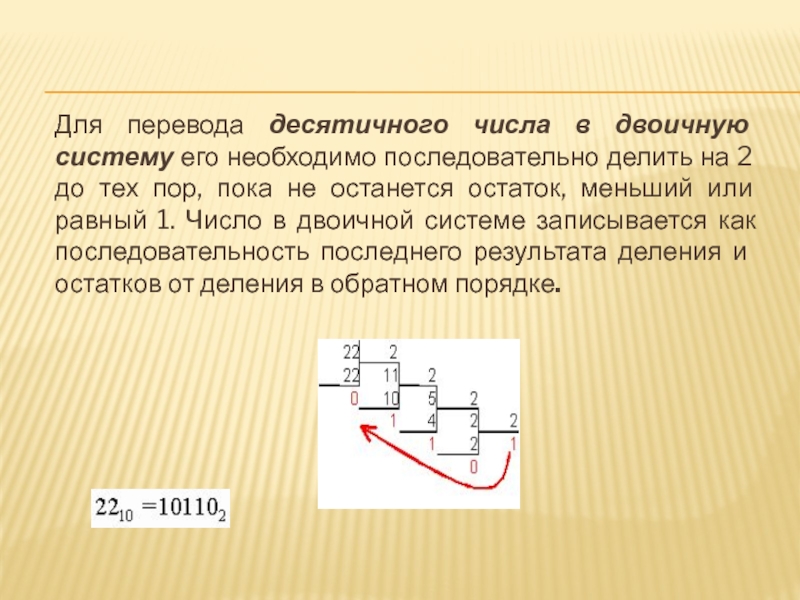
Слайд 21Для перевода десятичного числа в двоичную систему его необходимо последовательно
делить на 2 до тех пор, пока не останется остаток,
меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.Слайд 22Для перевода десятичного числа в восьмеричную систему его необходимо последовательно
делить на 8 до тех пор, пока не останется остаток,
меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.Пример. Число перевести в восьмеричную систему счисления.
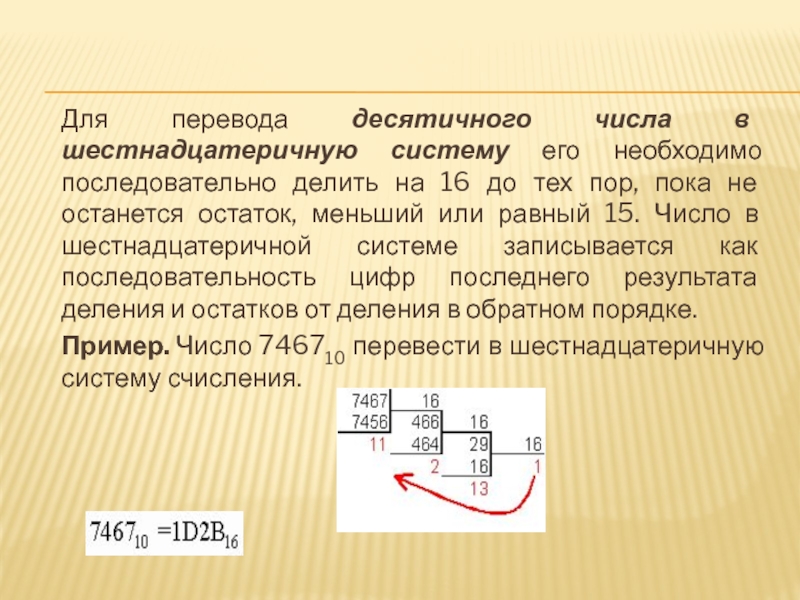
Слайд 23Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно
делить на 16 до тех пор, пока не останется остаток,
меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.Пример. Число 746710 перевести в шестнадцатеричную систему счисления.
Слайд 25Чтобы перевести число из двоичной системы в восьмеричную, его нужно
разбить на триады (тройки цифр), начиная с младшего разряда, в
случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифройПример. Число 10010112 перевести в восьмеричную систему счисления.
Слайд 26Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно
разбить на тетрады (четверки цифр), начиная с младшего разряда, в
случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифройПример. Число 10111000112 перевести в шестнадцатеричную систему счисления
Слайд 27Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить
эквивалентной ей двоичной триадой.
Пример. Число 5318 перевести в двоичную систему счисления.
Для перевода
шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.Пример. Число ЕЕ816 перевести в двоичную систему счисления.
Слайд 28При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно,
необходим промежуточный перевод чисел в двоичную систему.
Пример 1. Число FEA16 перевести в
восьмеричную систему счисленияПример 2. Число 66358 перевести в шестнадцатеричную систему счисления.