Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение векторов при решении задач и доказательстве теорем
Содержание
- 1. Применение векторов при решении задач и доказательстве теорем
- 2. ВВЕДЕНИЕ
- 3. Учёные всегда стремились упростить себе жизнь –
- 4. Интерес к векторам и векторному исчислению пробудился
- 5. 2.2. ВЕКТОРЫ Вектор-это отрезок, для которого указано,
- 6. ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫРисунок 2 - Изображение
- 7. Если через некоторую точку пространства проведены три
- 8. 4.2 Доказательство некоторых теоремПусть точки А, В, С
- 9. 4.3 Нахождение расстояний и угловНа рёбрах DA,DB,AC тетраэдра
- 10. 5.2 Задачи на построенияВершина В прямоугольного параллелепипеда АВСDA1B1C1D1
- 11. Аналогично если плоскость α пересекает ось Ву
- 12. 5.3 Задачи на вычисления расстояний и угловВ основании
- 13. векторов ВС и ВМ. Получаем B(-1;0;0;), K(-1/2;0;1/2),
- 14. Обобщая вышеизложенные доводы, мы удостоверились, что использование
- 15. 1. В.Б. Некрасов, Б.М. Беккер, «Применение векторов для
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2ВВЕДЕНИЕ
3
1 КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА 4
2 ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ 5
2.2. ВЕКТОРЫ 5
3 КООРДИНАТЫ 7
4 РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ВЕКТОРОВ И СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 8
4.2 ДОКАЗАТЕЛЬСТВО НЕКОТОРЫХ ТЕОРЕМ 8
4.3 НАХОЖДЕНИЕ РАССТОЯНИЙ И УГЛОВ 9
5 РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ 10
5.2 ЗАДАЧИ НА ПОСТРОЕНИЯ 10
5.3 ЗАДАЧИ НА ВЫЧИСЛЕНИЯ РАССТОЯНИЙ И УГЛОВ 12
ЗАКЛЮЧЕНИЕ 14
СПИСОК ЛИТЕРАТУРЫ 15
Содержание
Слайд 3Учёные всегда стремились упростить себе жизнь – придумывали новые, простые
методы решения, универсальные для множества задач, позволяющие быстро решить даже
самую трудную задачу. Именно таким методом и является векторно-координатный.«Векторный» путь построения геометрии предложил в 1918 году известный немецкий математик Герман Вейль. Векторы можно использовать как для решения планиметрических задач, так и для стереометрических.
Векторно-координатный метод решения задач позволяет с лёгкостью решать даже самые большие и сложные задачи, избегать долгих доказательств теорем. С помощью векторов можно вычислять расстояния и углы, доказывать теоремы, строить перпендикулярные и параллельные прямые и отрезки, строить сечения, доказывать равенство геометрических фигур и многое другое.
В настоящее время векторно-координатный метод используется в алгебре, геометрии, физике, механике; понятие векторного пространства используется в теории вероятностей, математической экономике, биологии, лингвистике и т.д.
3
ВВЕДЕНИЕ
Слайд 4Интерес к векторам и векторному исчислению пробудился у математиков в
XIX веке в связи с потребностями механики и физики. Однако
истоки исчисления с направленными отрезками возникли в далеком прошлом. В Древней Греции пифагорейцы, открыв иррациональные числа, которые нельзя выразить дробями (например:√2, √5), не решились ввести более широкое толкование числа. Математики того времени попытались свести вопросы арифметики и алгебры к решению задач геометрическим путем. Таким образом, было положено начало геометрической теории отношений Евдокса (408-355 гг. до н.э.), а позднее «геометрической алгебре». В геометрическом исчислении, изложенном, а труде Евклида «Начала», сложения и вычитания сводились к сложению и вычитанию отрезков, а умножение - к построению прямоугольников на отрезках, соответствующих по длине множителям.Термин «вектор» происходит от латинского слова vector, что означает несущий или ведущий, влекущий, переносящий
В современной математике раздел, в котором излагается учение о действиях над векторами, называют векторной алгеброй, так как эти действия имеют много общих свойств с алгебраическими действиями. 4
КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА
Слайд 52.2. ВЕКТОРЫ
Вектор-это отрезок, для которого указано, какой из его
концов считается началом, а какой – концом. Направление вектора на
рисунке (от начала к концу) отмечается стрелкой.(рисунок 1)5
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
Рисунок 1 - Изображение вектора
Любая точка пространства также может считаться вектором. В таком случае вектор называется нулевым. Начало и конец этого вектора совпадают.
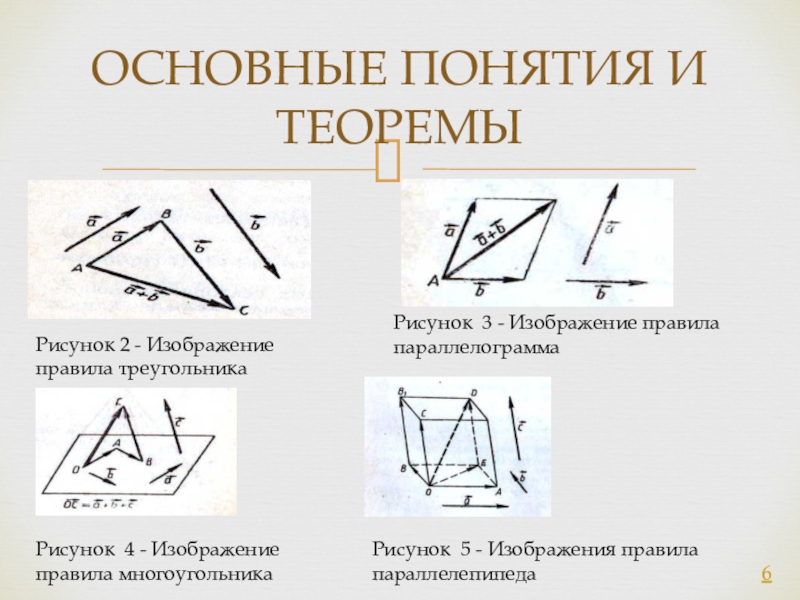
Слайд 6ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
Рисунок 2 - Изображение правила треугольника
Рисунок 3
- Изображение правила параллелограмма
Рисунок 4 - Изображение правила многоугольника
Рисунок 5
- Изображения правила параллелепипеда 6 Слайд 7Если через некоторую точку пространства проведены три попарно перпендикулярные прямые,
на каждой из них выбрано направление (оно обозначается стрелкой) и
выбрана единица измерения отрезков, то говорят, что выбрана прямоугольная система координат в пространстве. Прямые с выбранными направлениями называются осями координат, а их общая точка – началом координат. Она обычно обозначается буквой О. Оси обозначаются так: Ох, Оу, Оz – и имеют названия: «ось абсцисс», «ось ординат», «ось аппликат». Вся система координат называется Oxyz. Три плоскости, проходящие через оси координат называются координатными плоскостями. Точка О разделяет каждую из осей координат на на два дополнительных луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а дополнительный к нему луч – отрицательной полуосью.7
КООРДИНАТЫ
Слайд 84.2 Доказательство некоторых теорем
Пусть точки А, В, С и Р такие,
что ОР=mOA+nOB+рОС (OА, ОС и ОВ линейно независимы).Тогда необходимое и
достаточное условие их принадлежности одной прямой состоит в следующем: m+n+р=1. (рис 7)8
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ВЕКТОРОВ
Пусть точки А, В, С и Р лежат в одной плоскости, тогда векторы
АР=ОР-ОА, АВ=ОВ-ОА, АС=ОС-ОА будут линейно зависимыми, следовательно
ОР-ОА=n(OB-OA)+p(OC-OA),
OP=(1- n- p)OA+nOB+pOC. И в силу единственности разложения вектора OP по векторам ОА, ОВ, ОС получим
m=1- n –p или m+ n+ p=1
Доказательство достаточности:
Пусть m+n+p=1, тогда
OP-OA=mOA+nOB+pOC-OA=mOA+nOB+pOC-(m+n+p)*OA=n(OB-OA)+p(OC-OA)
Отсюда АР=nAB+pAС и по определению P принадлежит плоскости АВС.
Рисунок 7 - Изображение фигуры
Слайд 94.3 Нахождение расстояний и углов
На рёбрах DA,DB,AC тетраэдра DABC взяты соответственно
точки L, N, F так, что DL=1/2DA,DN=1/3DB,AF=1/4AC. В каком отношении
плоскость, проходящая через точки L,N,F делит ребро BC? (рис 8)РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ВЕКТОРОВ
Решение:
Пусть М – точка пересечения рассматриваемой плоскости с ребром BC и
DA=a, DB=b, DC=c.
Так как точки M,N,L,F лежат в одной плоскости, причём последние три точки не лежат на одной прямой, то по формуле
DM=kDL+lDN+(1 – k – l)DF=ka/2+lb/3+(1 – k – l)(3/4a+1/4c).
С другой стороны, по формуле (1)
DM=(1-m)b+mc
где m – отношение ВМ:ВС. Так как векторы а,b,с не компланарны, то на основании утверждения о разложении вектора по трём некомпланарным, мы получим систему:
k/2+(1 – k – l)3/4=0, l/3=1 – m,
(1 – k – l)1/4=m. 9
Отсюда m=2/5 и ВМ:МС=2/3.
Рисунок 8 - Изображение фигуры
Слайд 105.2 Задачи на построения
Вершина В прямоугольного параллелепипеда АВСDA1B1C1D1 с отношением рёбер
AB:DA:AA1=1:2:3 принята за начало прямоугольной системы координат, а
векторы ВА,
1/2ВС и 1/3ВВ1 приняты соответственно за единичные векторы i, j, k.Построить сечение параллелепипеда плоскостью α , заданной в этой системе координат уравнением 4x + y - 2z - 2=0. (рис 9)
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ
Рисунок 9 - Изображение фигуры
Для построения данного сечения найдём три точки, принадлежащие плоскости α, но не лежащие на одной прямой, например, точки пересечения плоскости α с осями координат. Так, если плоскость α пересекает ось Вх в точке К, то точка К имеет координаты (к;0;0). Подставляя эти координаты в уравнение плоскости α ,получим к=1/2. Таким образом, плоскость α пересекает ось Вх в точке К(1/2;0;0). Построим эту точку.
10
Слайд 11Аналогично если плоскость α пересекает ось Ву в точке L,
то точка L имеет координаты (0;l;0). Подставляя эти координаты в
уравнение плоскости α , найдем, что L(0;2;0). Построим точку L (она совпала с точкой С).Точно так же находим, что плоскость α пересекает ось Вz в точке М(0;0;-построим эту точку и затем построим сечение призмы плоскостью α, проходящей через точки К,L,M. Получаем четырёхугольник КСD2A2.
11
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ
Слайд 125.3 Задачи на вычисления расстояний и углов
В основании пирамиды МАВС лежит
равнобедренный треугольник с прямым углом при вершине С. каждое боковое
ребро образует с плоскостью основания угол, равный 45 гр. На ребре МВ взята точка К – середина этого ребра. Найдём угол между прямой АК и плоскостью МВС. (рис 10)РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ
Установив, что медианно МО грани МАВ является высотой пирамиды, т.е. МО┴АВ и МО┴ОС, и что ОА =ОС=ОМ, зададим в пространстве прямоугольную систему координат Охуz, как показано на рисунке.
OA=i ; OC=j ; OM=k
В этой системе координат O(0;0;0), A(1;0;0), C(0;1;0), M(0,0,1)
Находим далее координаты точек В и К, вектора АК, коллинеарного прямой АК, и
12
Слайд 13векторов ВС и ВМ. Получаем B(-1;0;0;), K(-1/2;0;1/2), AK(-3/2;0;1/2), BC(1;1;0), BM
(1;0;1).
Если вектор n(k;l;m) перпендикулярен плоскости МВС, то n┴BC и
n┴BM, или в координатах:k*1+l*1+m*0=0
k*1+l*0+m*1=0
откуда, полагая, например, что k=1, находим, что l=-1, m=-1, т.е. n(1;-1;-1).
Пусть φ – это искомый угол. Тогда
13
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ
Рисунок 11 - продолжение решения задачи
Таким образом, угол между прямой АК и плоскостью МВС равен arcsin (2√30)/15 Содержание
Слайд 14Обобщая вышеизложенные доводы, мы удостоверились, что использование векторно-координатного метода позволяет
с лёгкостью решать множество задач самых разных видов, избегать больших
доказательств теорем. Решение таким методом задачи, помогает сэкономить время и силы. Такое решение задач хорошо тем, что человек не механически действует по образцу решения задач данного типа, повторяя одни и те же действия, а творчески подходит к работе.14
ЗАКЛЮЧЕНИЕ
Слайд 151. В.Б. Некрасов, Б.М. Беккер, «Применение векторов для решения задач», СПб,
СМИО Пресс 2002г.
2. В.Н. Литвиненко «Сборник задач по стереометрии с методами
решений» М., изд. «Просвещение», 1998г3. Н.М. Рогановский, А.А. Столяр «Векторное построение стереометрии» изд. «Народная асвета»,1974г.
4. Ионин Ю.И., Некрасов В.Б. «Векторы в геометрических задачах»
5. Болтянский В.Г., Ягиом И.Н. «Векторы и их применение в геометрии в книге: Энциклопедия элементарной математики», том 4 М., Главное издательство физмат литературы, 1963г.
6. Журнал «Математика», №39, 2001г.
7. Зив Б.Г. «Задачи к урокам геометрии 7-11»СПб, МПО «Мир и семья – 95», изд. ООО «Акация», 1996г.
8. Атанасян Л.С., Бутузов В.Ф. и др. учебник «Геометрия 9-10»Изд. «Просвещение», 1982г. 15
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ