Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признаки параллельности прямых
Содержание
- 1. Признаки параллельности прямых
- 2. I признак параллельностиЕсли при пересечении двух прямых
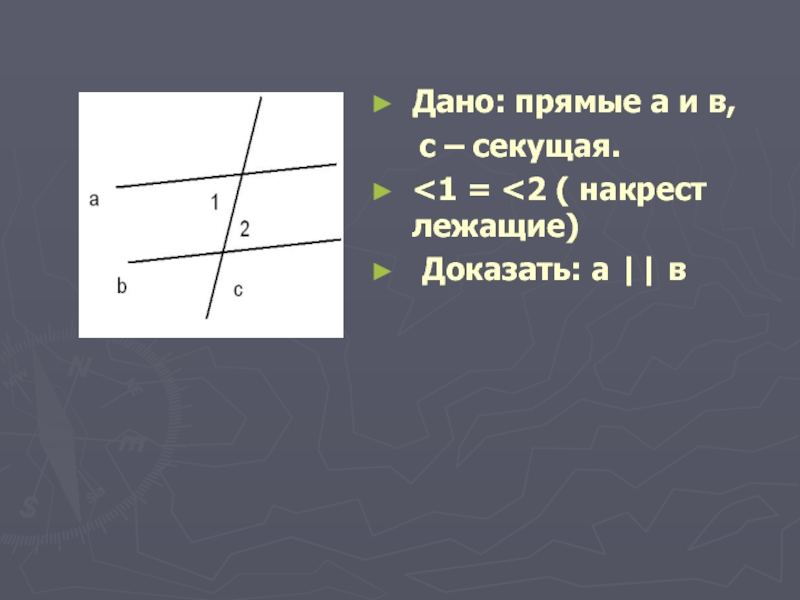
- 3. Дано: прямые а и в, с – секущая.
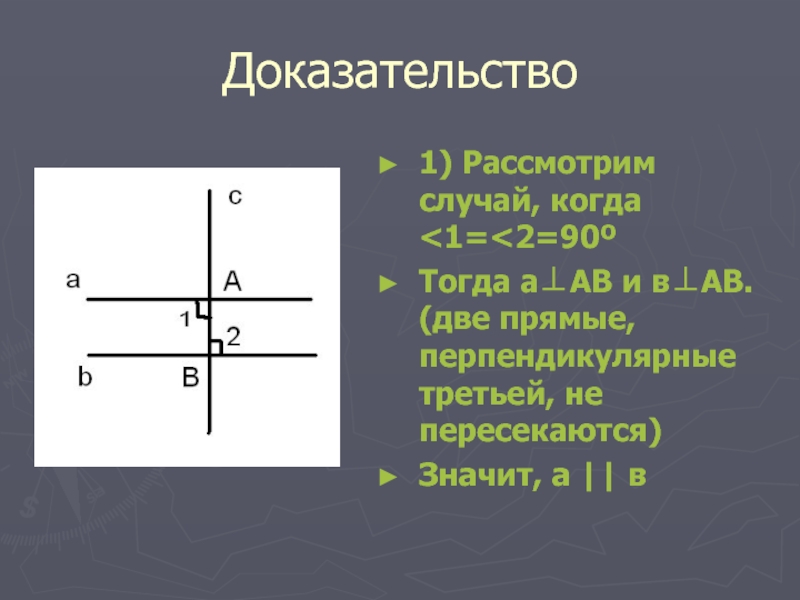
- 4. Доказательство1) Рассмотрим случай, когда
- 5. 2случай)
- 6. II признак параллельности. Если при пересечении двух
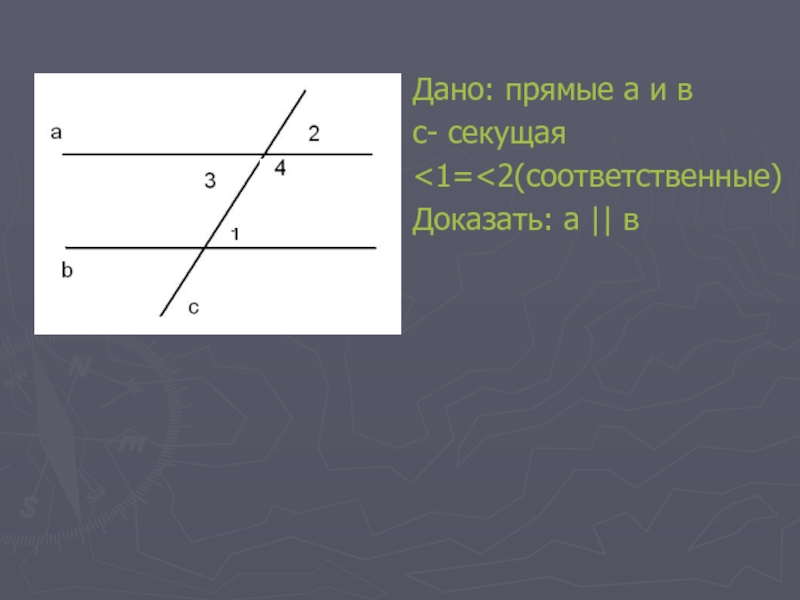
- 7. Дано: прямые а и вс- секущая
- 8. Доказательство
- 9. III признак параллельностиЕсли при пересечении двух прямых секущей сумма односторонних углов равна 180º, то прямые параллельны.
- 10. Доказательство
- 11. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2I признак параллельности
Если при пересечении двух прямых секущей накрест лежащие
углы равны, то такие прямые параллельны.
Слайд 4Доказательство
1) Рассмотрим случай, когда
перпендикулярные третьей, не пересекаются)
Значит, а || в
Слайд 52случай)
построению)
АН=ВН₁ ( по построению)
так, что АО=ВО. Проведем ОН⊥а.Отложим ВН₁ = АН, соединим О с Н₁
а
в
с
А
В
О
Н
Н₁
1
2
3
4
⇒∆ОНА = ∆ОН₁В ( по 2 сторонам м углу между ними) Так как <3=<4 ,то точка Н₁∊ на продолжении луча ОН. Значит, точки О,Н и Н₁ лежат на одной прямой.
⇒<3=<4 и
Так как
( две прямые, перпендикулярные третьей, не пересекаются) : а || в
Слайд 6II признак параллельности
. Если при пересечении двух прямых
секущей соответственные углы равны, то прямые параллельны.
Слайд 9III признак параллельности
Если при пересечении двух прямых секущей сумма односторонних
углов равна 180º, то прямые параллельны.
Слайд 10Доказательство
в , секущая с
они накрест лежащие при пересечении прямых
а и в и секущей с
⇒ по первому признаку параллельности
а || в