РАСЧЕТЫ НА ЖЕСТКОСТЬ ПРИ ПРЯМОМ ПЛОСКОМ ИЗГИБЕ. Перемещения при

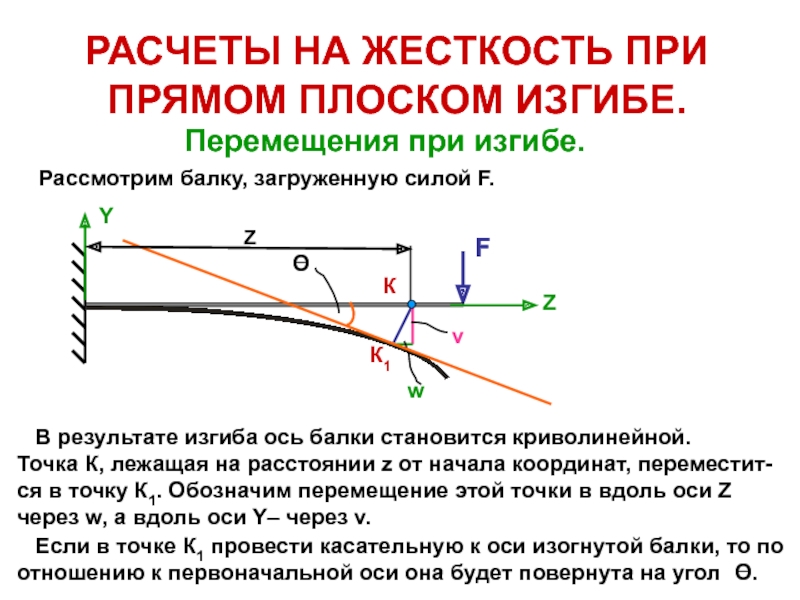
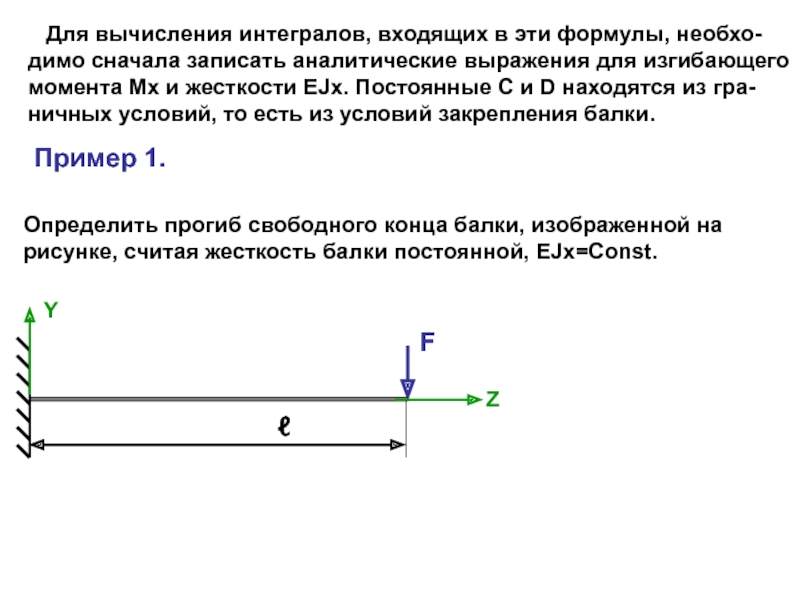
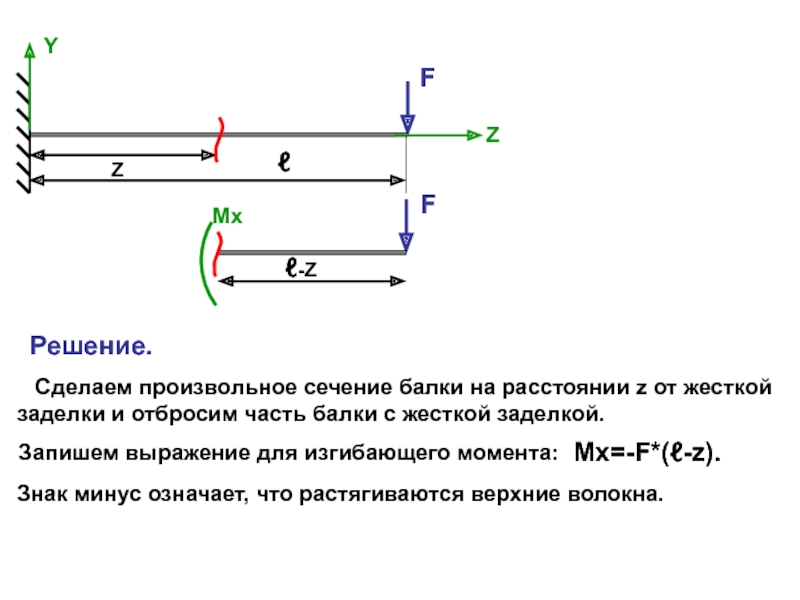
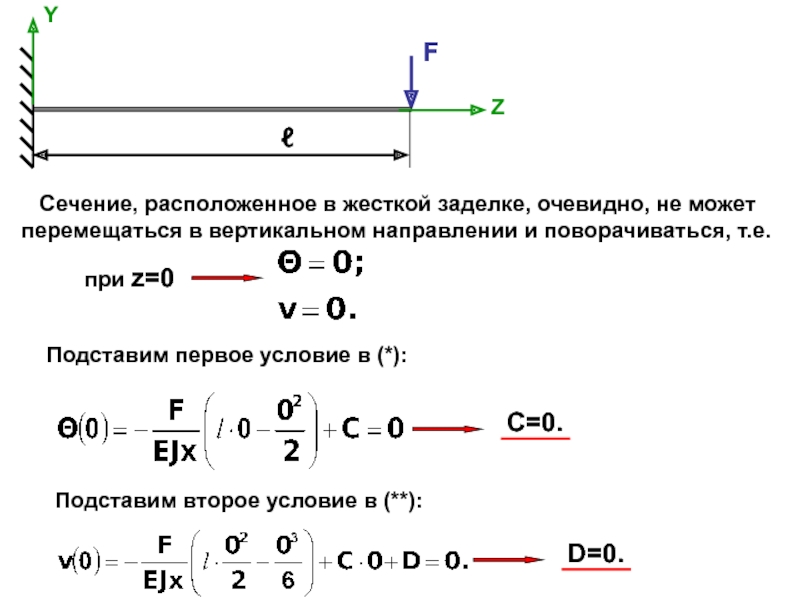
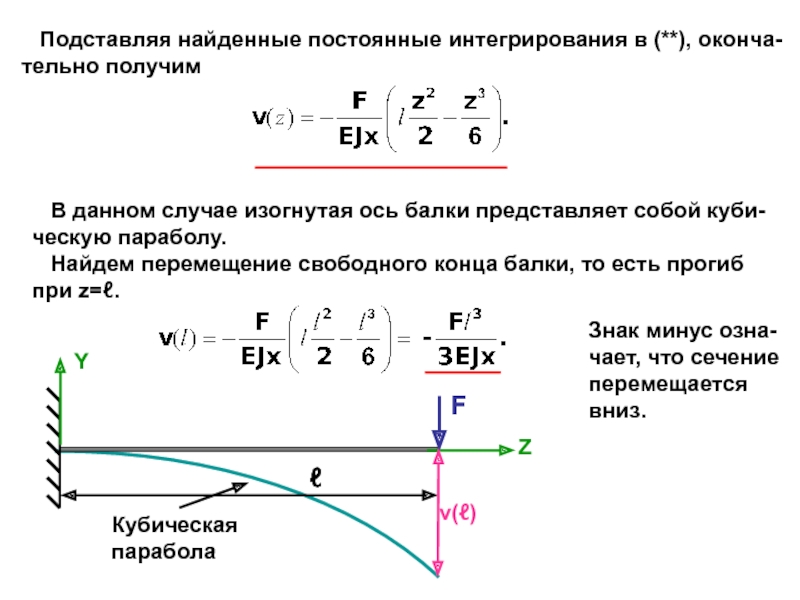
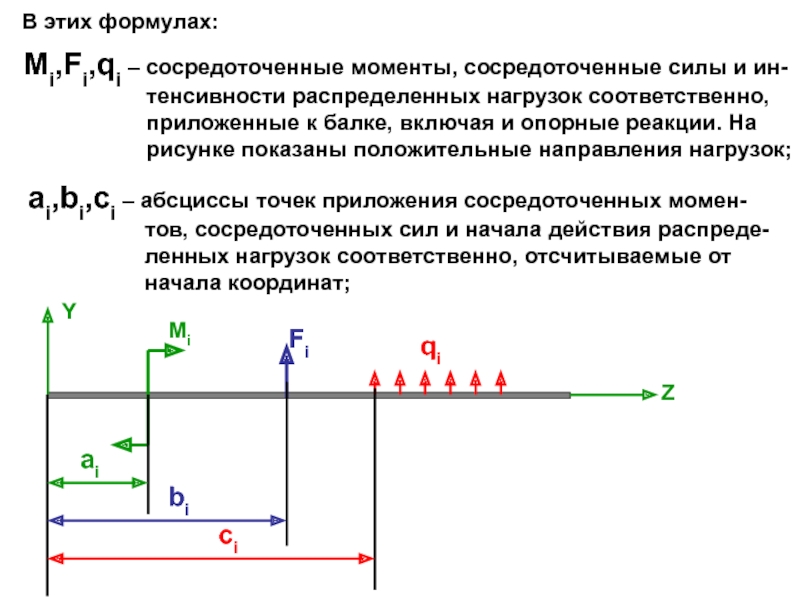
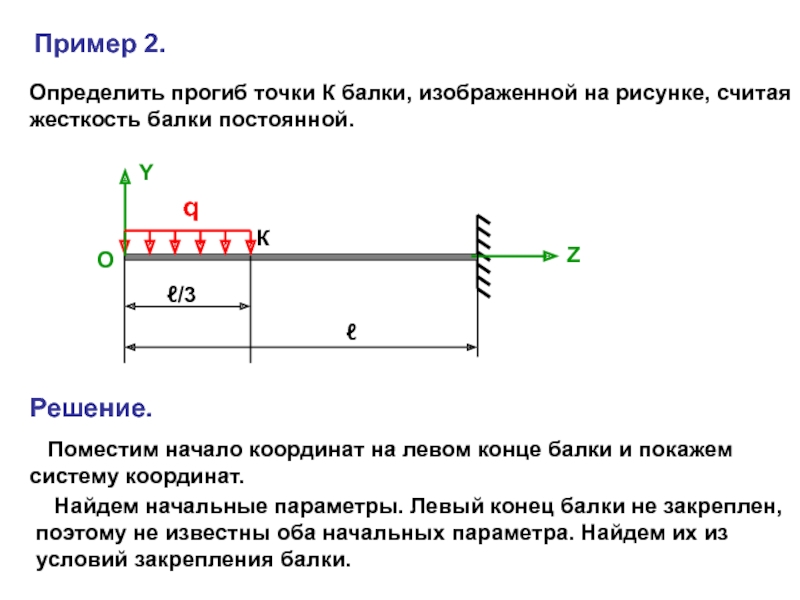
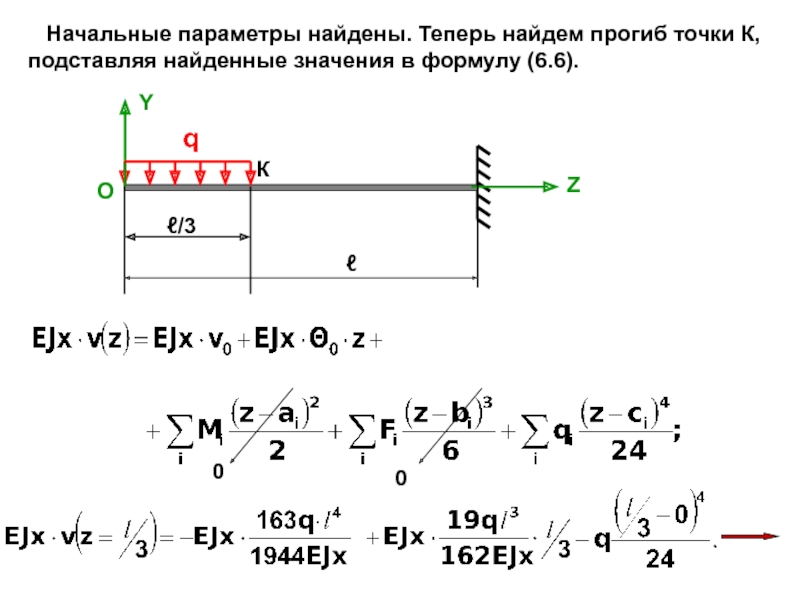
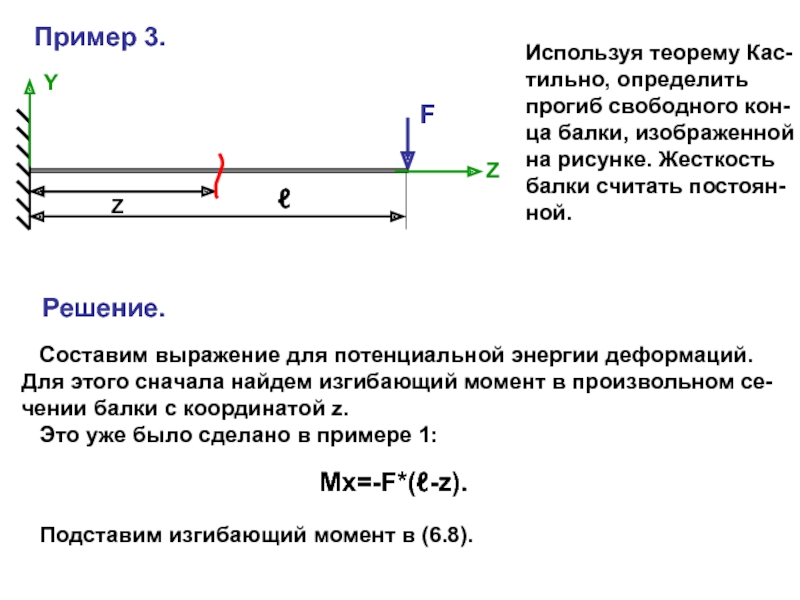
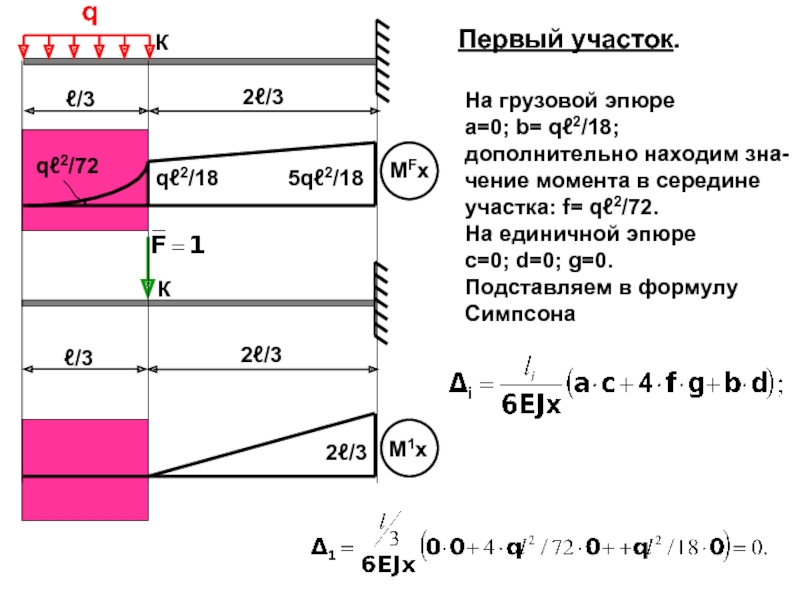
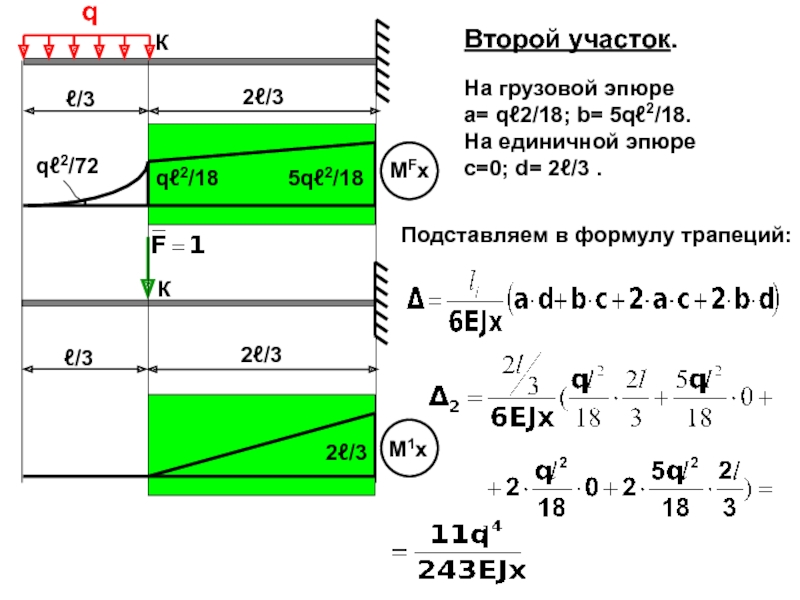
Рассмотрим балку, загруженную силой F.
w
В результате изгиба

ось балки становится криволинейной.
Точка К, лежащая на расстоянии z от начала координат, переместит-
ся в точку К1. Обозначим перемещение этой точки в вдоль оси Z
через w, а вдоль оси Y– через v.

Если в точке К1 провести касательную к оси изогнутой балки, то по
отношению к первоначальной оси она будет повернута на угол .

F

Z

К

К1

Y

v

Z

изги-
бе весьма малы по сравнению с размерами балки; обычно
Это позволяет

ввести некоторые упрощения:
1) при малых вертикальных перемещениях v горизонтальными пе-
ремещениями w пренебрегаем, так как можно показать, что они бу-
дут малыми второго порядка. Тогда можно считать, что точки оси
балки перемещаются только по вертикали;
ось изогнутой балки является графиком функции v(z), и, согласно

геометрическому смыслу производной, ;

F

Z

К

К1

Y

w

v

ℓ

F

Z

К

Y

v

v(z)

К1

оси изогнутого бруса также очень мал и тогда
(6.1)
v(z)

будет
равен углу Θ( они будут равны, как углы между взаимно

перпе-
дикулярными прямыми).
В дальнейшем угол Θ будем называть углом поворота. Верти-
кальное перемещение v принято называть прогибом. Эти две ве-
личины являются компонентами перемещения точек при изгибе.

К

К1

Сделаем еще один чертеж балки, показав на этот раз ее толщину.
В процессе деформации сечение, проведенное через точку К по-
вернется.

напряжений при чистом
изгибе была получена связь между кривизной и изгибающим

мо-
ментом:

(6.2)

Из этой формулы следует, что кривизна балки изменяется по тому
же закону, что и величина Mx/EJx. Так, если сечение балки постоян-
но, балка выполнена из одного и того же материала, то при чистом
изгибе

ρ=const, то есть при чистом из-
гибе балка изгибается по окружности.

Однако в общем случае поперечного изгиба пользоваться форму-
лой (6.2) для определения прогибов весьма затруднительно. В этом
случае применяют известное из математического анализа выраже-
ние для кривизны:

уранение от-
носительно прогибов:
По допущению (2) угол
тогда окончательно

получим

(6.3)

Выражение (6.3) называется дифференциальным уравнением оси
изогнутого бруса. Если ось Y направлена вверх, то в уравнении
выбирают знак плюс. Произведение EJx называется жесткостью
при изгибе.

интегрирования.
Этот метод основан на интегрировании уравнения (6.3). Проинте-
грировав

это уравнение один раз, получим выражение для угла по-
ворота:

(6.4)

Проинтегрировав (6.4), получим выражение для прогибов:

(6.5)

Если результат вычислений оказывается положительным, то про-
гиб направлен вверх, то есть совпадает с положительным напра-
влением оси Y.

сначала записать аналитические выражения для изгибающего
момента Mx и жесткости EJx.

Постоянные C и D находятся из гра-
ничных условий, то есть из условий закрепления балки.

Пример 1.

F

Y

ℓ

Z

Определить прогиб свободного конца балки, изображенной на
рисунке, считая жесткость балки постоянной, EJx=Const.

жесткой
заделки и отбросим часть балки с жесткой заделкой.

Запишем выражение для

изгибающего момента:

Знак минус означает, что растягиваются верхние волокна.

Mx

еще раз:
(*)
(**)
Найдем постоянные интегрирования из граничных условий.

перемещаться в вертикальном направлении и поворачиваться, т.е.
при z=0
Подставим первое условие

в (*):

С=0.

Подставим второе условие в (**):

D=0.

В данном случае изогнутая ось балки представляет собой куби-
ческую

параболу.
Найдем перемещение свободного конца балки, то есть прогиб
при z=ℓ.

Кубическая
парабола

ℓ

Z

Y

F

v(ℓ)

Знак минус озна-
чает, что сечение
перемещается
вниз.

функцию прогибов балки, что позволя-
ет при необходимости, построив график этой

функции, изобразить
изогнутую ось балки. Недостатком же этого метода является трудо-
емкость вычислений при увеличении количества участков загруже-
ния балки. Так, если балка имеет, например, три участка загружения,
то при интегрировании образуется шесть постоянных интегрирова-
ния, для определения которых надо решать систему шести уравне-
ний. Именно вследствие этого недостатка метод непосредственного
интегрирования редко применяется в инженерной практике.

Метод начальных параметров.

Этот метод был разработан группой советских ученых на основе
метода непосредственного интегрирования, но, в отличие от него,
здесь, независимо от количества участков загружения, необходимо
будет определять только две постоянных интегрирования – прогиб
и угол поворота в начале координат. Перемещения в этом методе
находятся с помощью двух формул (даны без вывода).

ин-

тенсивности распределенных нагрузок соответственно,
приложенные к балке, включая и опорные реакции. На
рисунке показаны положительные направления нагрузок;

ai,bi,ci – абсциссы точек приложения сосредоточенных момен-
тов, сосредоточенных сил и начала действия распреде-
ленных нагрузок соответственно, отсчитываемые от
начала координат;

В этих формулах:

координат, называемые
начальными

параметрами.

z– координата сечения, в котором определяется перемещение.

При использовании этих формул необходимо соблюдать следую-
щие правила:
1). Начало координат всегда выбирается на левом конце балки;

О

распо-
ложены слева от рассматриваемого сечения;

3). В

случае, если действие распределенной нагрузки заканчива-
ется раньше рассматриваемого сечения, ее продлевают до этого
сечения, а для восстановления действительных грузовых условий
вводят «компенсирующую» нагрузку обратного направления. До-
полнительную и компенсирующую нагрузку на расчетной схеме
обычно показывают пунктиром;

qi

Y

Z

qi

Дополнительная
нагрузка

Компенсирующая
нагрузка

4). Если результат вычислений оказывается положительным, то
прогиб направлен вверх, то есть совпадает с положительным на-
правлением оси Y.

самих начальных параметров. При этом могут встре-
титься следующие случаи:

1). Левый конец балки жестко защемлен. Тогда заданы оба на-
чальных параметра:

v0=0;
Θ0=0.

2). Левый конец балки шарнирно оперт. Тогда задан один на-
чальный параметр:

а

v0=0;
Θ0 находим из условия
v(а)=0.

3). Левый конец балки свободен. Тогда неизвестны оба началь-
ных параметра:

а

с

v0,Θ0 находим из условий
v(a)=0;
v(c)=0.

жесткость балки постоянной.
Решение.
q
Y
Z
ℓ
Поместим начало координат на левом конце

балки и покажем
систему координат.

О

Найдем начальные параметры. Левый конец балки не закреплен,
поэтому не известны оба начальных параметра. Найдем их из
условий закрепления балки.

К

ℓ/3

опре-
деления начальных параметров запишутся в виде:
v(ℓ)=0;

Θ(ℓ)=0.
(*)
(**)
Подставим условие (**) в

формулу (6.7), при этом учтем, что распре-
деленная нагрузка не доходит до сечения z=ℓ и необходимо ввести
дополнительную и компенсирующую нагрузку той же интенсивности.

К

ℓ/3

найденные значения в формулу (6.6).
0
0

К
перемещается вниз.
q
К
vK

формулы потенциаль-
ной энергии деформаций. По аналогии с осевым растяжением-сжа-
тием запишем

формулу для определения потенциальной энергии
при изгибе:

Как показывают расчеты, при изгибе балок вклад поперечной си-
лы в величину U пренебрежимо мал по сравнению с вкладом изги-
бающего момента, поэтому в дальнейшем будем определять потен-
циальную энергию по упрощенной формуле:

(6.8)

Для вывода теоремы
Кастильяно рассмотрим
упругую систему в виде
однопролетной балки,
загруженной двумя не-
зависимыми

силами F1
и F2.

1

2

V1

V2

Под действием этих сил балка прогибается , при этом сечение 1 прогибается на величину V1, а сечение 2 – на величину V2 (рис.1).
Потенциальная энергия деформации этой балки определяется
окончательными значениями внешних сил и не зависит от порядка
их приложения. Найти эту энергию можно путем сложения работ сил при любой последовательности их приложения (на основании
гипотезы о независимости действия сил).

рис.1

F1 сечения 1 и 2
перемещаются на вели-
чины V11 и V21

соответст-
венно (рис.2).

F1

F2

V11

V21

F1

F2

2

V1

V2

F2

2

рис.1

рис.2

Работу силы F1 на пе-
ремещении V11 найдем
по формуле (2.22):

Приложим теперь к уже
изогнутой балке силу
F2. Сечения 1 и 2 полу-
чат дополнительные
перемещения V12 и V22
соответственно (рис.3).
Из рисунков следует,
что V1=V11+V12 и
V2=V21+V22.

рис.3

1

1

V12

V22

2

формуле
(2.22),
Сила F1 в процессе нагружения балки силой

F2 остается неизмен-
ной, поэтому ее работу вычисляем по обычной формуле теорети-
ческой механики:

Потенциальная энергия деформаций будет равна сумме этих
работ:

В теме «Осевое растяжение-сжатие» было показано, что в зоне
упругих деформаций, перемещения прямо пропорционально вы-
зывающей их силе:

перепишется в виде:
V11=k*F1.
(*)
Продифференцируем это выражение по силе F1.

При этом учтем,
что перемещения V12, V22 не зависят от этой силы.

С учетом (*) получим

силы F2, то получим
Если нагрузить балку вместо сосредоточенной

силы сосредото-
ченным моментом, то, продифференцировав выражение для поте-
нциальной энергии по этому моменту, получим величину угла по-
ворота. Таким образом, можно сформулировать теорему Кастиль-
яно следующим образом:
« Частная производная от потенциальной энергии деформаций по
сосредоточенной нагрузке равна перемещению сечения, в котором
эта нагрузка приложена».
Если результат вычислений положителен, то направление пере-
мещения совпадает с направлением соответствующей нагрузки.

на рисунке. Жесткость
балки считать постоян-
ной.
Решение.
Составим выражение для потенциальной

энергии деформаций.
Для этого сначала найдем изгибающий момент в произвольном се-
чении балки с координатой z.
Это уже было сделано в примере 1:

Подставим изгибающий момент в (6.8).

Знак плюс указывает на то, что направление перемещения совпа-
дает с

направлением действующей силы, то есть прогиб напра-
влен вниз ( сравни с результатом примера 1).

сечения, к которому не приложена нагрузка. Однако из этого затруд-
нения

есть простой выход. Чтобы определить прогиб или угол пово-
рота в точке, где по условию задачи сила отсутствует, в этой точке
следует приложить соответствующую фиктивную нагрузку. Далее,
написав выражение для потенциальной энергии от системы сил,
включая фиктивную нагрузку, следует взять производную от этого
выражения по фиктивной нагрузке и в полученном выражении для
перемещения положить фиктивную нагрузку равной нулю.
Рассмотрим этот процесс применительно к изгибу балки.

в которой не приложены никакие нагрузки.
Приложим в точке К

фиктивную силу Ф.

Ф

Запишем выражение для изгибающего момента в произвольном сечении балки. На основании принципа независимости действия
сил

-- изгибающий момент от заданных нагрузок;

-- изгибающий момент от фиктивной нагрузки.

Последний, очевидно, можно переписать в виде:

где

-- изгибающий момент от фиктивной нагрузки, равной
единице, Ф=1, который называется единичным моментом.

для потенциальной энергии деформаций:
Теперь «вспомним», что на самом деле нагрузки

Ф нет, и в полу-
ченное выражение подставим Ф=0.

(6.9)

можно определять и прогиб, и угол поворота.
При определении прогиба в

качестве фиктивной нагрузки берут
безразмерную сосредоточенную силу, равную единице, а при оп-
ределении угла поворота фиктивной нагрузкой является безраз-
мерный сосредоточенный момент, также равный единице.

Знак плюс результата указывает на то, что направление переме-
щения совпадает с направлением единичной фиктивной нагрузки.

Метод Мора по сравнению с другими рассмотренными методами
обладает одним очень важным преимуществом – он является уни-
версальным в смысле выбора вида деформации и объекта приме-
нения, то есть его можно использовать при определении перемеще-
ний не только при изгибе, но и при растяжении, сжатии, кручении;
и не только балок,но и рам, арок, ферм, пространственных брусь-
ев и т.д.

на рисунке.
Жесткость балки счи-
тать постоянной.
Решение.

Найдем

изгибающий момент в произвольном сечении балки с координатой z от заданной нагрузки, то есть от силы F.
Это уже было сделано в примере 3:

К

М=1

а

Поскольку по условию задачи требуется найти угол поворота в
точке К, приложим в этой точке безразмерный фиктивный момент
М=1.

Теперь запишем момент от единичной нагрузки:

при

при

Знак плюс результата указывает на то, что направление переме-
щения совпадает

с направлением единичного момента, то есть се-
чение К поворачивается по часовой стрелке.

для изгибающих моментов
MF и M1. Это особенно неудобно при определении

перемещений в
брусе, имеющим большое количество участков загружения. Однако,
если брус состоит из участков с постоянной в пределах каждого
участка жесткостью EJx, операцию вычисления интеграла Мора мож-
но значительно упростить, применяя для этого формулы численного
интегрирования – формулу трапеций или формулу Симпсона.
В этом случае для определения перемещений какого-либо сечения
балки необходимо выполнить следующие операции:
1) построить так называемую грузовую эпюру, то есть эпюру изги-
бающих моментов MF от заданной нагрузки;
2) построить единичную балку, то есть снять с рассматриваемой
балки все нагрузки, и к сечению, перемещение которого надо опре-
делить, приложить фиктивную силу, равную единице, если надо оп-
ределить прогиб, или фиктивный момент, равный единице, если оп-
ределяется угол поворота;
3) построить так называемую единичную эпюру, то есть эпюру из-
гибающих моментов M1 от фиктивной нагрузки;
4) разбить обе эпюры на участки перемножения;

используя формулу трапеций, если на грузовая эпюра на
участке ограничена прямой

линией, или формулу Симпсона, кото-
рая применима и для прямолинейных, и для криволинейных участ-
ков (см. ниже).
6) сложить полученные результаты.

a,b и c,d– значения изгиба-
ющих моментов на границах участка перемножения

на грузовой и
единичной эпюрах соответственно; f,g – значения моментов в сере-
динах участков.

Участок грузовой
эпюры

Участок единичной
эпюры

плюс, если соответ-
ствующие отрезки на эпюрах моментов лежат по одну

сторону от
осей, и со знаком минус, если по разные.

ac>0; ad>0; bc>0; bd>0.

ac>0; ad>0; bc<0; bd<0.

рисунке, считая жесткость балки постоянной.
Решение.
q
ℓ

К
ℓ/3

требуется определить
прогиб т.К, приложим на еди-
ничной балке в т.К безразме-
рную

единичную силу.

ℓ/3

2ℓ/3

К

3). Построим единичную эпю-
ру, то есть эпюру изгибаю-
щих моментов M1x для еди-
ничной балки.

qℓ2/18

5qℓ2/18

2ℓ/3

1). Построим эпюру изги-бающих моментов для дан-ной балки, то есть грузо-вую эпюру MFx. В дальней-шем эпюры, предназна-ченные для определения перемещений, штриховать не будем.

обоим участ-
кам формулы численного
интегрирования. На первом
участке грузовая эпюра кри-
волинейна,

поэтому там
необходимо применить
формулу Симпсона; на вто-
ром участке можно приме-
нять любую формулу.

зна-
чение момента в середине
участка: f= qℓ2/72.
На единичной эпюре
с=0; d=0; g=0.
Подставляем

в формулу
Симпсона

единичной эпюре
с=0; d= 2ℓ/3 .

Подставляем в формулу трапеций:

Знак плюс результата указывает на то, что направление переме-
щения

совпадает с направлением единичной фиктивной нагрузки,
то есть сечение К перемещается вниз (сравни результаты
примера 2).