Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Раздел № 3 Солодухин Е.А
Содержание
- 1. Раздел № 3 Солодухин Е.А
- 2. Слайд 2
- 3. Плоскость
- 4. Плоскость это один из видов поверхности – плоская поверхность.
- 5. Способы задания плоскостиГ(А,В,С)Т(А,l )Σ(mn)Ω(n II m)(ΔABC)
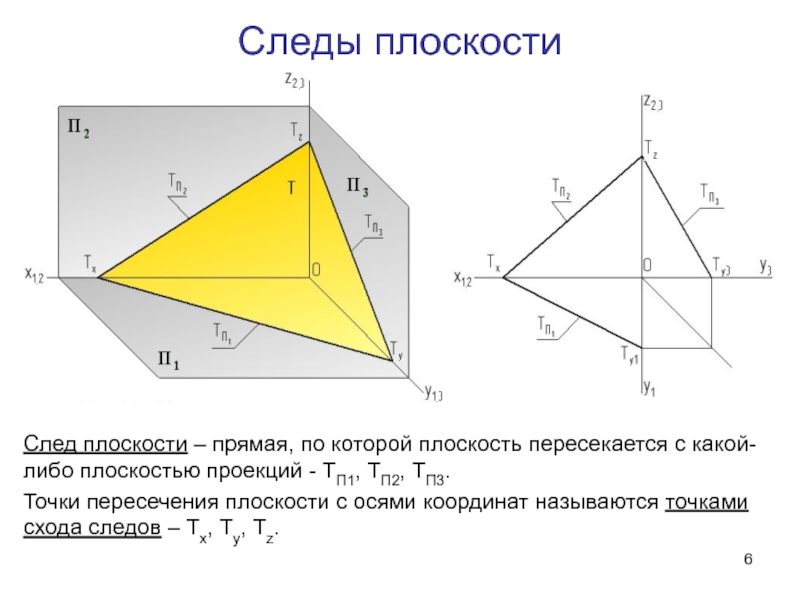
- 6. Следы плоскостиСлед плоскости – прямая, по которой
- 7. Положение плоскости относительно плоскостей проекций
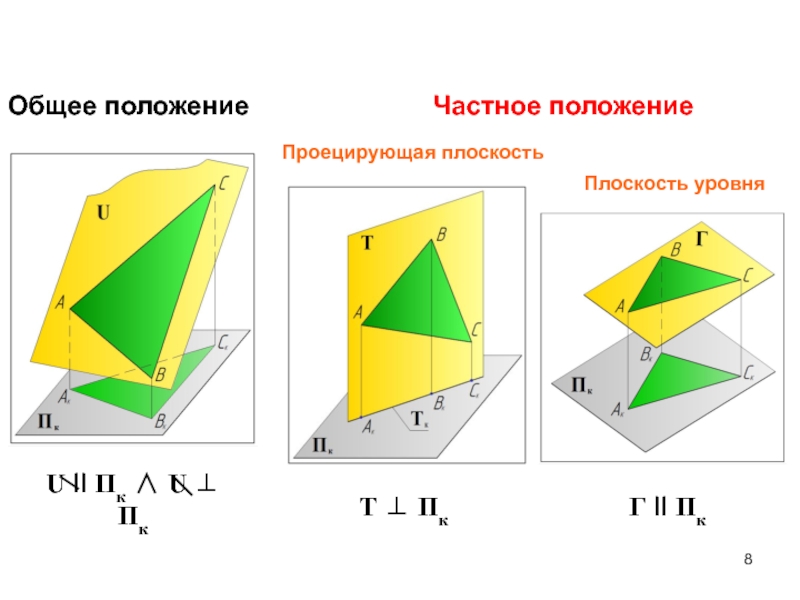
- 8. U II Пк U ПкОбщее положениеЧастное положениеТ ПкГ II Пк Проецирующая плоскостьПлоскость уровня
- 9. Плоскость общего положенияПлоскость непараллельная и неперпендикулярная плоскостям
- 10. Плоскости частного положения
- 11. Это плоскости перпендикулярные одной из плоскостей проекцийГоризонтально-проецирующаяФронтально-проецирующаяТ1
- 12. Это плоскости параллельные одной из плоскостей проекцийГоризонтальная
- 13. У плоскости частного положения одна из проекций обязательно имеет форму прямой линии. Вывод:
- 14. Прямая на плоскости Прямая принадлежит
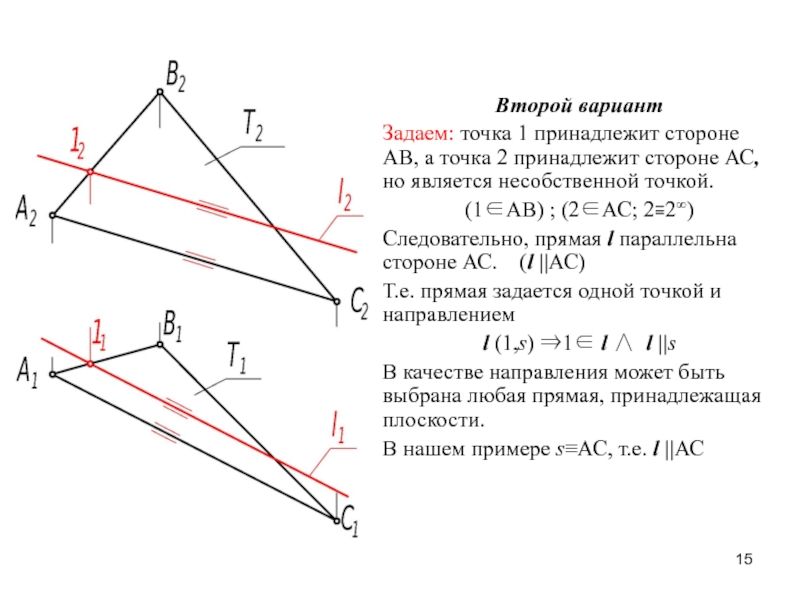
- 15. Второй вариантЗадаем: точка 1 принадлежит стороне АВ,
- 16. Главные линии плоскостиК главным линиям плоскости относятся
- 17. Прямые уровня плоскости
- 18. Горизонталь плоскостиПлоскость ТАВСПостроить h Тh 1
- 19. Фронталь плоскостиПлоскость ТАВСПостроить f Тf 2
- 20. Линии наибольшего наклона плоскостиДанные линии применяются для
- 21. Линия наибольшего ската плоскостиТ – плоскость общего
- 22. Плоскость ТАВСПостроить проекции линии наибольшего ската l
- 23. Точка на плоскости
- 24. Точка принадлежит плоскости, если она
- 25. А l ; l (1,2)
- 26. Взаимное положение двух плоскостей
- 27. Параллельные плоскости
- 28. Две плоскости параллельны, если две пересекающиеся прямые
- 29. Пересекающиеся плоскости
- 30. Т ∩ P(∆АВС)= l
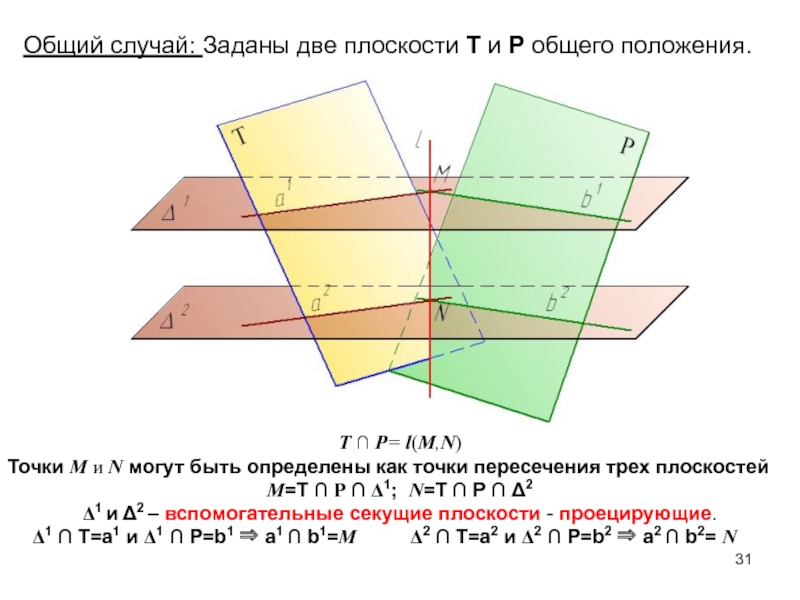
- 31. Т ∩ P= l(M,N)Точки M и N
- 32. Слайд 32
- 33. Взаимное положение прямой линии и плоскости
- 34. Прямая по отношению к плоскости может занимать следующие положения:Принадлежать;Быть параллельной;Пересекать;Быть перпендикулярной.
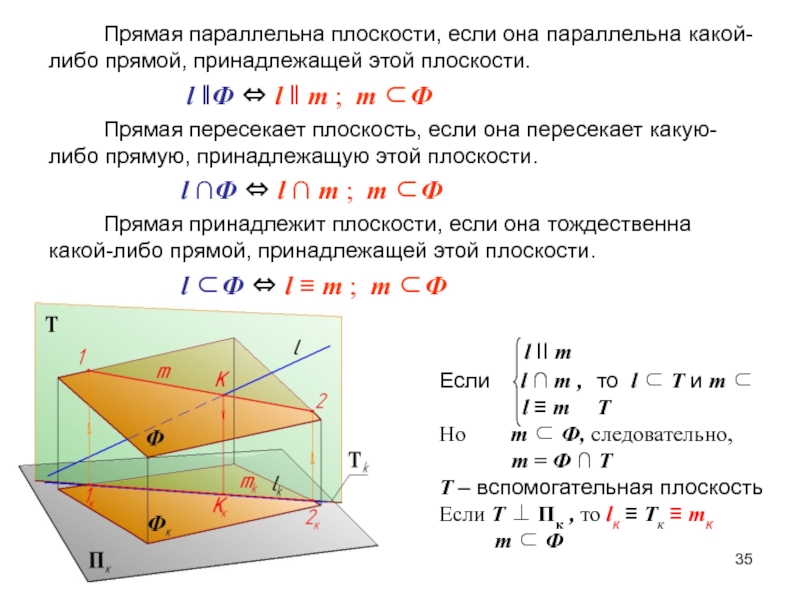
- 35. Прямая параллельна плоскости, если она параллельна какой-либо
- 36. Последовательность действий при определении взаимного положения прямой
- 37. Пример 11.Выбрано l1≡ m12. m(1,2); 1=m∩АВ; 2=m
- 38. Пример 21.Выбрано l1≡ m12. m(1,2); 1=m∩АВ; 2=m
- 39. Пример 31.Выбрано l2≡ m22. m(1,2); 1=m∩АВ; 2=m
- 40. Прямая перпендикулярная плоскости
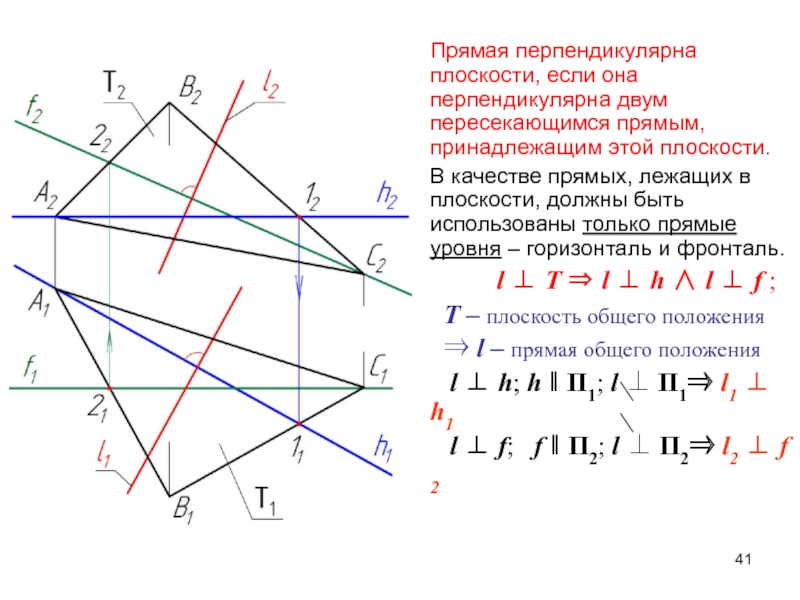
- 41. Прямая перпендикулярна плоскости, если она перпендикулярна двум
- 42. Взаимно перпендикулярные плоскости
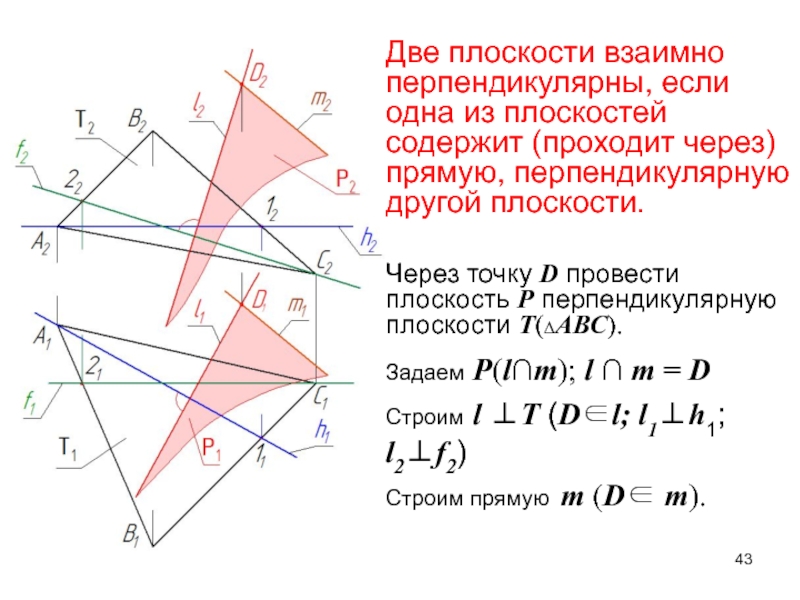
- 43. Две плоскости взаимно перпендикулярны, если одна из
- 44. Скачать презентанцию
Слайды и текст этой презентации
Слайд 6Следы плоскости
След плоскости – прямая, по которой плоскость пересекается с
какой-либо плоскостью проекций - ТП1, ТП2, ТП3.
Точки пересечения плоскости с
осями координат называются точками схода следов – Тх, Ту, Тz.Слайд 8U II Пк U Пк
Общее положение
Частное положение
Т
Пк
Г II Пк
Проецирующая плоскость
Плоскость уровня
Слайд 9Плоскость общего положения
Плоскость непараллельная и неперпендикулярная плоскостям проекций
Ни одна из
проекций плоскости не имеет форму прямой линии
Слайд 11Это плоскости перпендикулярные одной из плоскостей проекций
Горизонтально-проецирующая
Фронтально-проецирующая
Т1 – прямая и
Т1≡ ТП1
Т2 – прямая и Т2≡ ТП2
Проецирующие плоскости
Т П1
Т
П2Слайд 12Это плоскости параллельные одной из плоскостей проекций
Горизонтальная плоскость
Фронтальная плоскость
Плоскости уровня
Г
II П1
Т II П2
Г2 – прямая и Г2≡ ГП2
и Г2II x1,2Т1 – прямая и Т1≡ ТП1
и Т1 II x1,2
АВСТ АВС II П1А1В1С1 АВС
АВСТ АВС II П2А2В2С2 АВС
Слайд 13У плоскости частного положения одна из проекций обязательно имеет форму
прямой линии.
Вывод:
Слайд 14Прямая на плоскости
Прямая принадлежит плос-кости, если две
точки прямой принадлежат этой плоскости.
l (1,2) Т ⇔ (1Т )
(2Т)Принимаем: плоскость ТАВС.
Построить l Т.
Первый вариант
Задаем:
точка 1 принадлежит стороне АВ,
точка 2 принадлежит стороне ВС.
(1АВ) (2ВС)
Слайд 15
Второй вариант
Задаем: точка 1 принадлежит стороне АВ, а точка 2
принадлежит стороне АС, но является несобственной точкой.
(1АВ) ; (2АС;
2≡2∞)Следовательно, прямая l параллельна стороне АС. (l ||АС)
Т.е. прямая задается одной точкой и направлением
l (1,s) 1 l l ||s
В качестве направления может быть выбрана любая прямая, принадлежащая плоскости.
В нашем примере sАС, т.е. l ||АС
Слайд 16Главные линии плоскости
К главным линиям плоскости относятся прямые уровня -
горизонталь, фронталь, профильная прямая, и линии наибольшего наклона плоскости.
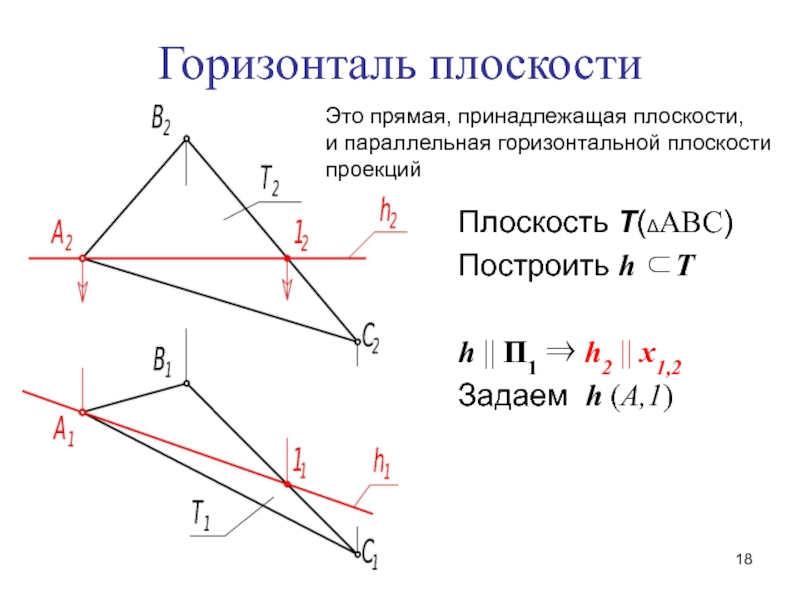
Слайд 18Горизонталь плоскости
Плоскость ТАВС
Построить h Т
h 1 h2
x1,2
Задаем h (А,1)
Это прямая, принадлежащая плоскости,
и параллельная горизонтальной плоскости
проекций
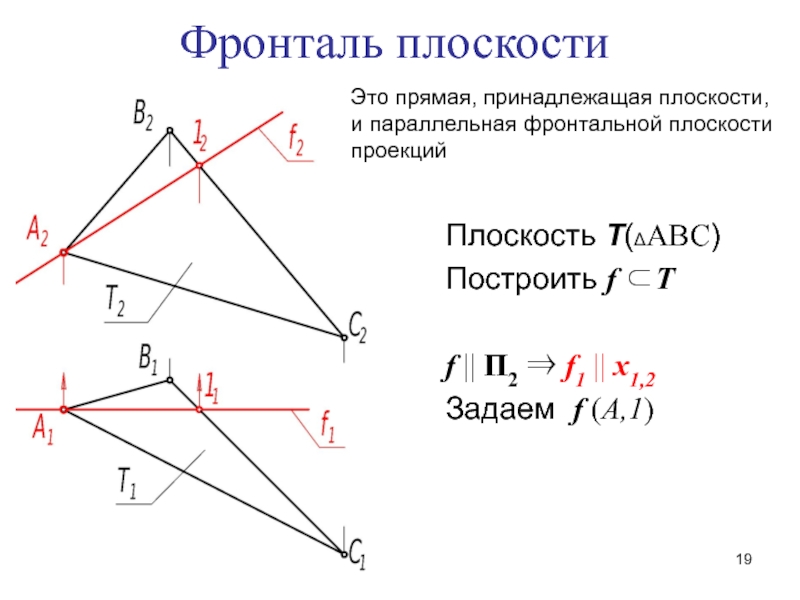
Слайд 19Фронталь плоскости
Плоскость ТАВС
Построить f Т
f 2 f1
x1,2
Задаем f (А,1)
Это прямая, принадлежащая плоскости,
и параллельная фронтальной плоскости
проекций
Слайд 20Линии наибольшего наклона плоскости
Данные линии применяются для опреде-ления величины угла
наклона плоскости к какой-либо плоскости проекций.
В частности, линия наибольшего наклона
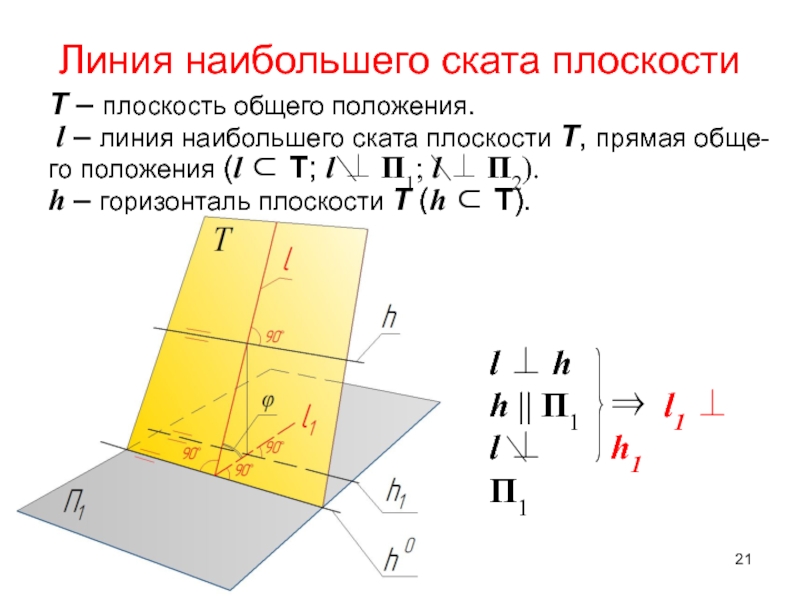
плоскости, используемая для определения угла наклона к горизонтальной плоскости проекций, получила название линии наибольшего ската плоскости.Слайд 21Линия наибольшего ската плоскости
Т – плоскость общего положения.
l –
линия наибольшего ската плоскости Т, прямая обще-го положения (l ⊂
Т; l П1; l П2).h – горизонталь плоскости Т (h ⊂ Т).
l h
h П1
l П1
l1 h1
Слайд 22Плоскость ТАВС
Построить проекции линии наибольшего ската l плоскости Т.
Так как
l Т, то задаем
l(В,2) ;
2 АССтроим l1 h1
Слайд 24 Точка принадлежит плоскости, если она принадлежит прямой, принадлежащей
этой плоскости
А Ф А l , l
Ф Слайд 28Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости.
Т(a∩b);
P(c∩d);
aIIc;
bIId; T II P
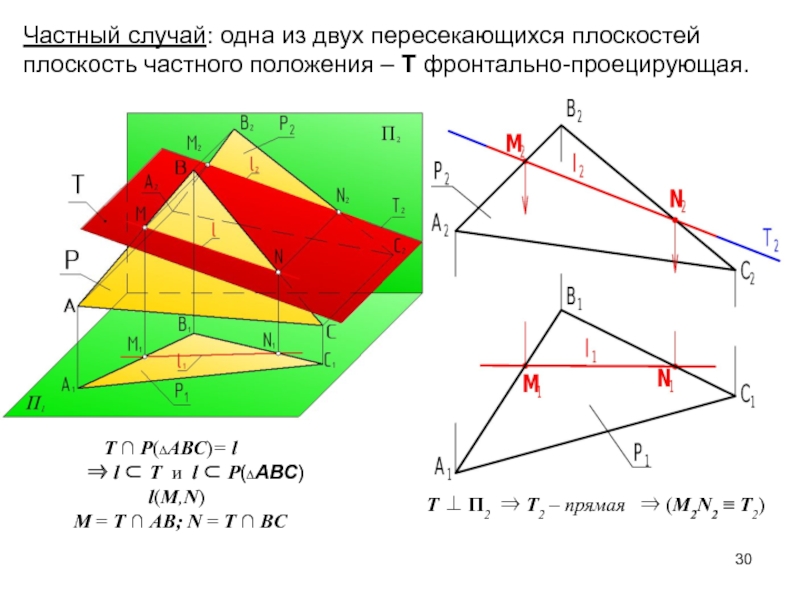
Слайд 30 Т ∩ P(∆АВС)= l
l
Т и l P(∆АВС)
l(M,N)M = Т ∩ AB; N = Т ∩ BC
Т П2 Т2 – прямая (M2N2 ≡ Т2)
Частный случай: одна из двух пересекающихся плоскостей плоскость частного положения – Т фронтально-проецирующая.
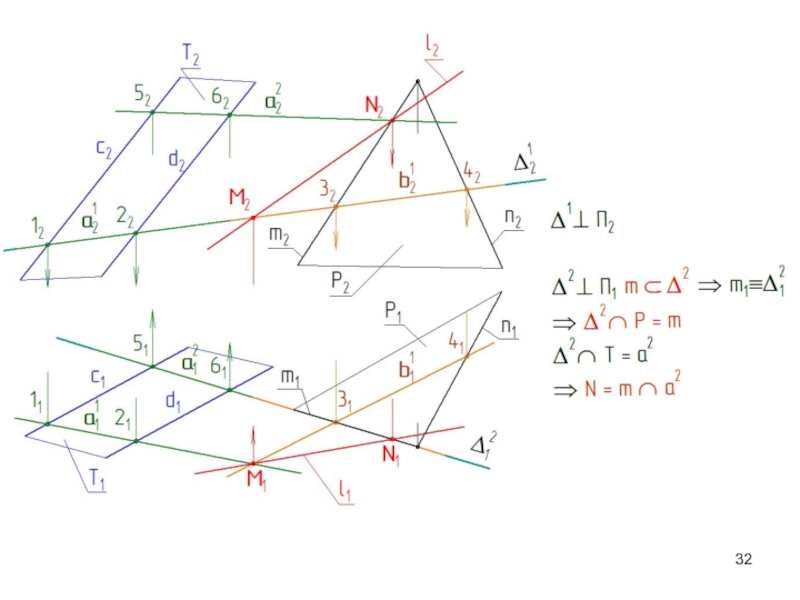
Слайд 31Т ∩ P= l(M,N)
Точки M и N могут быть определены
как точки пересечения трех плоскостей
М=Т ∩ Р ∩
Δ1; N=Т ∩ Р ∩ Δ2 Δ1 и Δ2 – вспомогательные секущие плоскости - проецирующие.
Δ1 ∩ Т=a1 и Δ1 ∩ Р=b1 a1 ∩ b1=М Δ2 ∩ Т=a2 и Δ2 ∩ Р=b2 a2 ∩ b2= N
Общий случай: Заданы две плоскости Т и Р общего положения.
Слайд 34Прямая по отношению к плоскости может занимать следующие положения:
Принадлежать;
Быть параллельной;
Пересекать;
Быть
перпендикулярной.
Слайд 35Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой
плоскости.
l ‖Ф
l ‖ m ; m ФПрямая пересекает плоскость, если она пересекает какую-либо прямую, принадлежащую этой плоскости.
l ∩Ф l ∩ m ; m Ф
Прямая принадлежит плоскости, если она тождественна какой-либо прямой, принадлежащей этой плоскости.
l Ф l ≡ m ; m Ф
l II m
Если l ∩ m ,
l ≡ m
Но m Ф, следовательно,
m = Ф ∩ T
T – вспомогательная плоскость
Если T Пк , то lк ≡ Tк ≡ mк
m Ф
то l T и m T
Слайд 36Последовательность действий при определении взаимного положения прямой линии и плоскости
Пример.
Заданы прямая l и плоскость Ф(АВС).
Одну из проекций заданной прямой
l, которую условно будем называть первой, совместить с одноименной проекцией вспомогательной прямой, например m. Прямую m нужно рассматривать как принадлежащую заданной плоскости Ф( АВС).lk≡ mk ; k =1, 2; m Ф ( АВС)
На рисунке l1≡ m1
Построить недостающую (условно вторую) проекцию вспомогательной прямой m.
если (m1≡ l1) то строиться m2;
если (m2≡ l2) то строиться m1.
3. На построенной (условно второй) проекции определить взаимное положение прямой l и вспомогательной прямой m.
если (m≡ l), то l Ф,
если (m ‖ l), то l ‖Ф,
если (m ∩ l), то l ∩Ф
На примере (l ∩ m=К, К= l ∩Ф ).
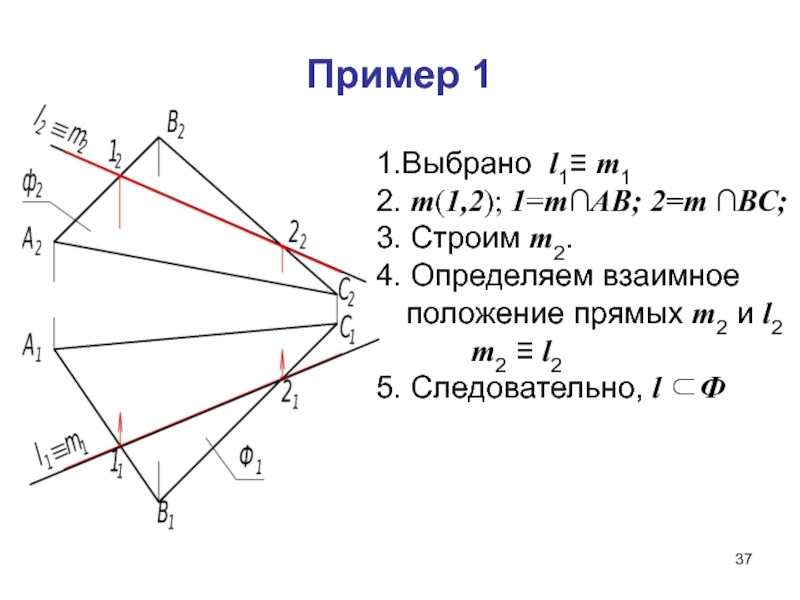
Слайд 37Пример 1
1.Выбрано l1≡ m1
2. m(1,2); 1=m∩АВ; 2=m ∩ВС;
3. Строим m2.
4.
Определяем взаимное положение прямых m2 и l2
m2 ≡ l25. Следовательно, l Ф
Слайд 38Пример 2
1.Выбрано l1≡ m1
2. m(1,2); 1=m∩АВ; 2=m ∩ВС;
3. Строим m2.
4.
Определяем взаимное положение прямых m2 и l2
m2 ∩ l2 = К25. Следовательно, l ∩Ф=К
Слайд 39Пример 3
1.Выбрано l2≡ m2
2. m(1,2); 1=m∩АВ; 2=m ∩ВС;
3. Строим m1.
4.
Определяем взаимное положение прямых m1 и l1
m1 ‖ l15. Следовательно, l ‖ Ф
Слайд 41Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим
этой плоскости.
В качестве прямых, лежащих в плоскости, должны быть использованы
только прямые уровня – горизонталь и фронталь.l T l h l f ;
Т – плоскость общего положения
l – прямая общего положения
l h; h ‖ П1; l П1 l1 h1
l f; f ‖ П2; l П2 l2 f 2
Слайд 43Две плоскости взаимно перпендикулярны, если одна из плоскостей содержит (проходит
через) прямую, перпендикулярную другой плоскости.
Через точку D провести плоскость Р
перпендикулярную плоскости Т(АВС).Задаем Р(l∩m); l ∩ m = D
Строим l T (Dl; l1h1; l2f2)
Строим прямую m (D m).