Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач на нахождение объемов и площадей поверхностей тел
Содержание
- 1. Решение задач на нахождение объемов и площадей поверхностей тел
- 2. Домашнее задание
- 3. Найдите объём многогранника, изображённого на рисунке (все
- 4. Конус вписан в цилиндр. Объем конуса равен
- 5. Ответ: 8
- 6. 2. Если каждое ребро куба увеличить на
- 7. 3. Гранью параллелепипеда является ромб со стороной
- 8. 4. Через среднюю линию основания треугольной призмы,
- 9. 5. Стороны основания правильной шестиугольной пирамиды равны
- 10. 6. Найдите объем пирамиды, изображенной на рисунке.
- 11. 7. Основанием пирамиды служит прямоугольник, одна боковая
- 12. 8. От треугольной пирамиды, объем которой равен
- 13. 9. Во сколько раз объем конуса, описанного
- 14. Скачать презентанцию
Домашнее задание
Слайды и текст этой презентации
Слайд 3 Найдите объём многогранника, изображённого на рисунке
(все двугранные углы многогранника прямые).
Найдите
объем пространственного креста, изображенного на рисунке и составленного из единичных
кубов.Ответ: 28
Ответ: 7
Слайд 4Конус вписан в цилиндр. Объем конуса равен 5. Найдите объем
цилиндра.
Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус
сферы.Ответ: 15
Ответ: 3
Слайд 62. Если каждое ребро куба увеличить на 1, то его
площадь поверхности увеличится на 30. Найдите ребро куба и его
объем.
Слайд 73. Гранью параллелепипеда является ромб со стороной 1 и острым
углом 60о. Одно из ребер параллелепипеда составляет с этой гранью
угол в 60о и равно 2. Найдите объем параллелепипеда
Слайд 84. Через среднюю линию основания треугольной призмы, объем которой равен
32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной
призмыРешение: Площадь основания отсеченной призмы равна четверти площади основания исходной призмы. Высота отсеченной призмы равна высоте исходной призмы. Следовательно, объем отсеченной призмы равен четверти объема исходной призмы, т.е. равен 8
Ответ: 8
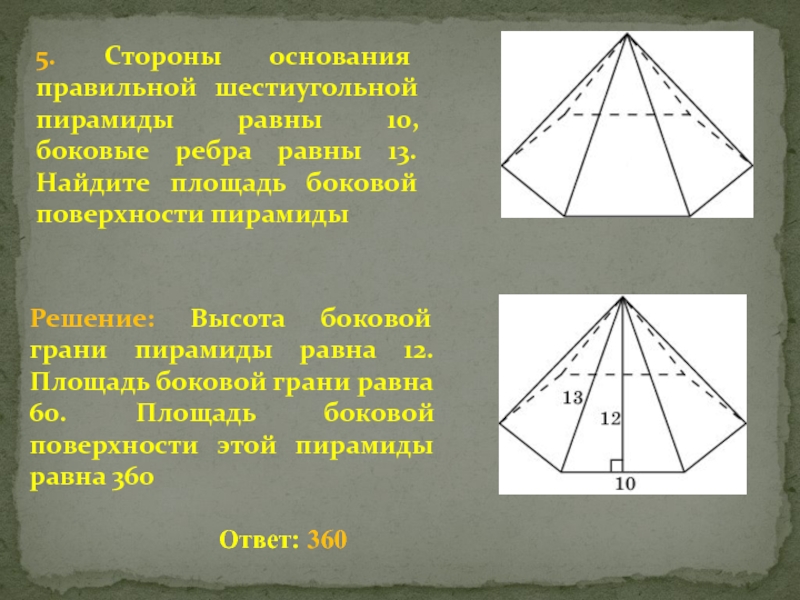
Слайд 95. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра
равны 13. Найдите площадь боковой поверхности пирамиды
Решение: Высота боковой
грани пирамиды равна 12. Площадь боковой грани равна 60. Площадь боковой поверхности этой пирамиды равна 360 Ответ: 360
Слайд 106. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является
многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер
перпендикулярно плоскости основания и равно 3Решение: Площадь основания пирамиды равна 27, высота равна 3. Следовательно, объем пирамиды равен 27.
Ответ: 27
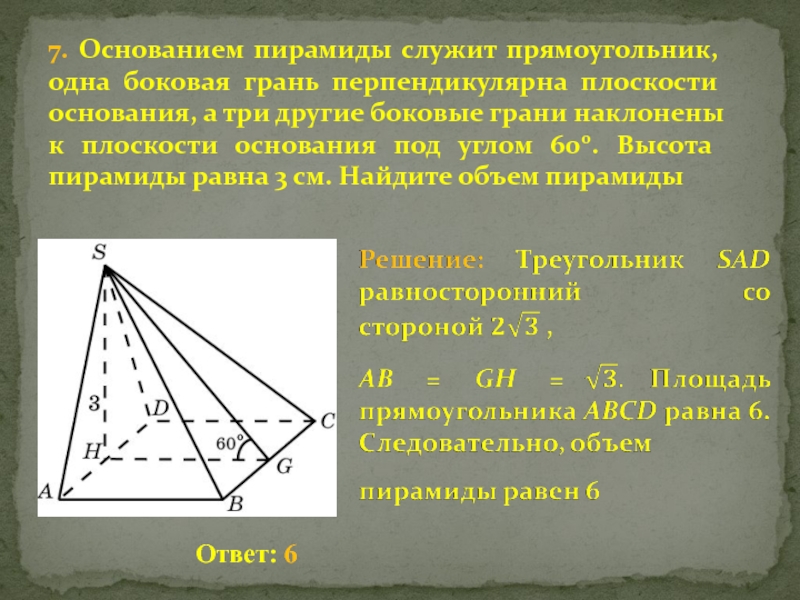
Слайд 117. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости
основания, а три другие боковые грани наклонены к плоскости основания
под углом 600. Высота пирамиды равна 3 см. Найдите объем пирамидыОтвет: 6
Слайд 128. От треугольной пирамиды, объем которой равен 12, отсечена треугольная
пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания.
Найдите объем отсеченной треугольной пирамиды.Ответ: 3
Слайд 139. Во сколько раз объем конуса, описанного около правильной четырехугольной
пирамиды, больше объема конуса, вписанного в эту пирамиду?
Ответ: 2
