Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ,
Содержание
- 1. САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ,
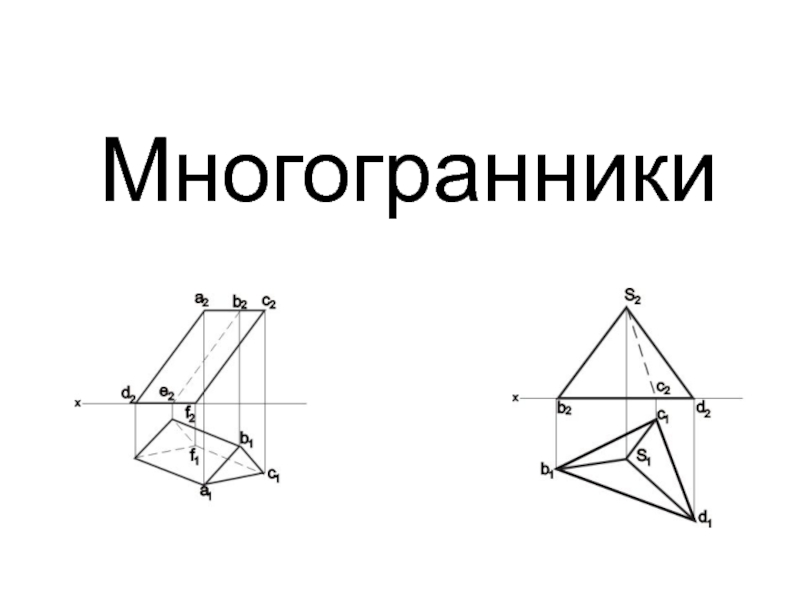
- 2. Многогранники
- 3. МногогранникиМногогранник в трехмерном пространстве - совокупность конечного
- 4. Виды многогранников Пирамида - это многогранник, одна
- 5. Виды многогранниковПризма - многогранник, две грани которого
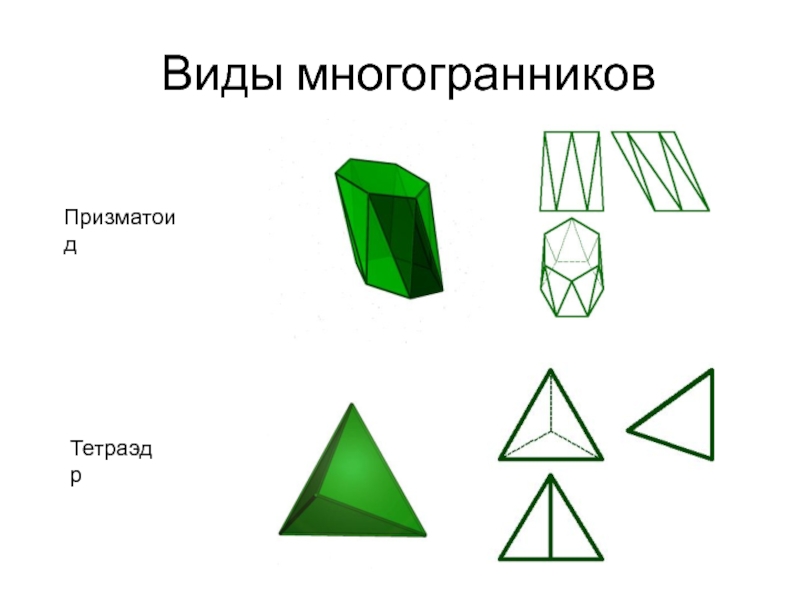
- 6. Виды многогранниковПризматоидТетраэдр
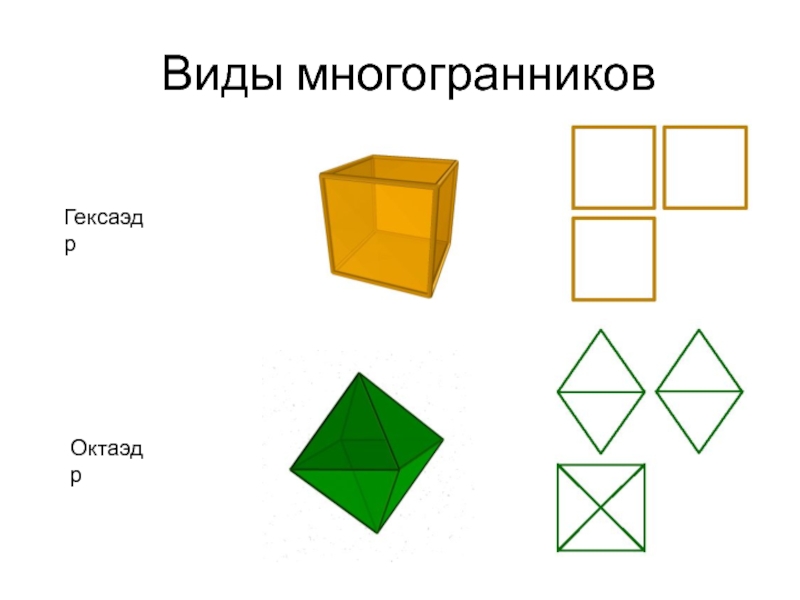
- 7. Виды многогранниковГексаэдрОктаэдр
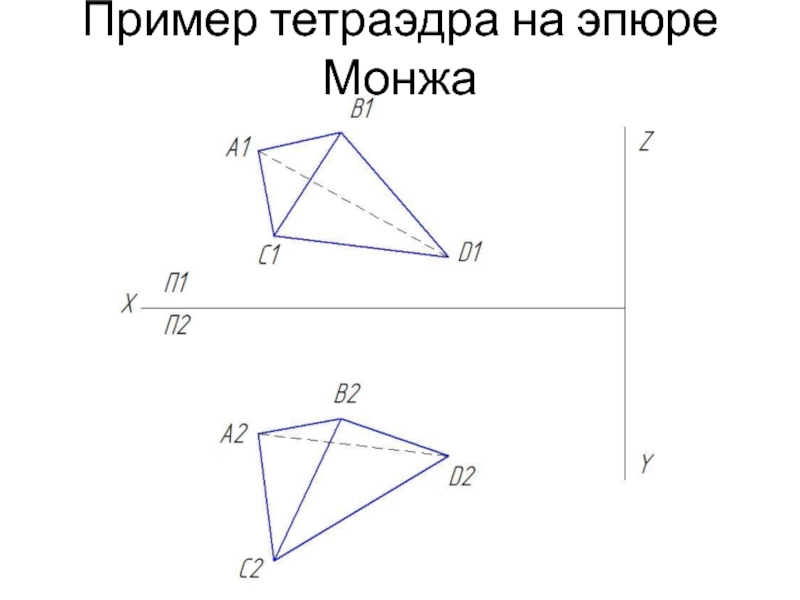
- 8. Пример тетраэдра на эпюре Монжа
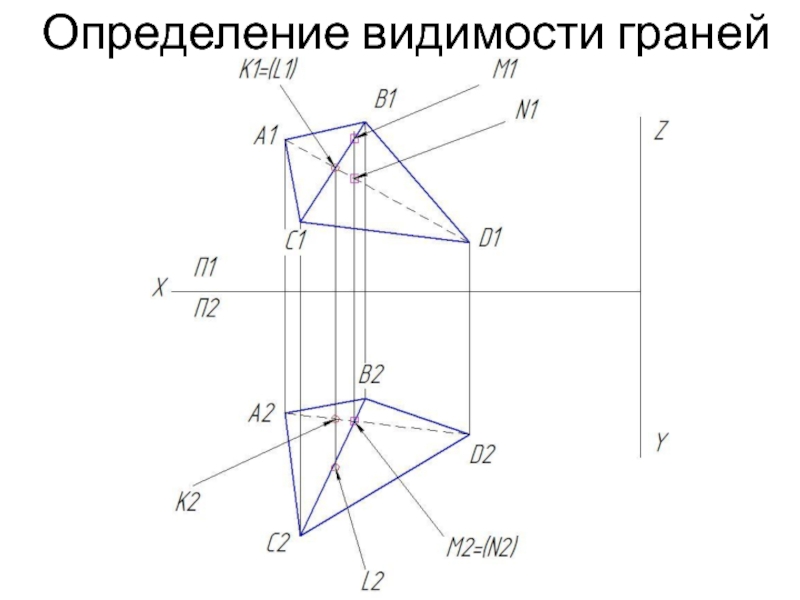
- 9. Определение видимости граней
- 10. Краткий экскурс в теорию Определение длины
- 11. Метод прямоугольного треугольникаДлину отрезка АВ и a
- 12. Метод прямоугольного треугольникаДлину отрезка АВ и b-угол
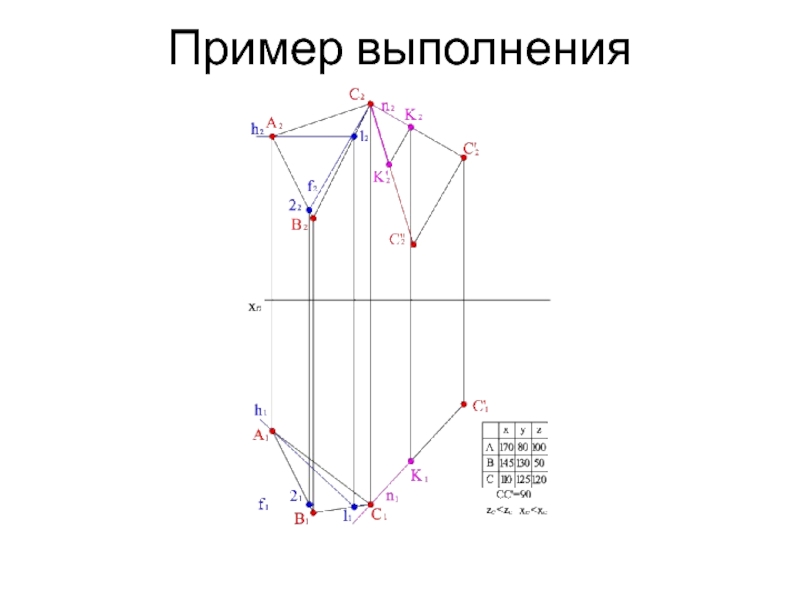
- 13. Лабораторная работа «Призма»Задание. По координатам трех точек,
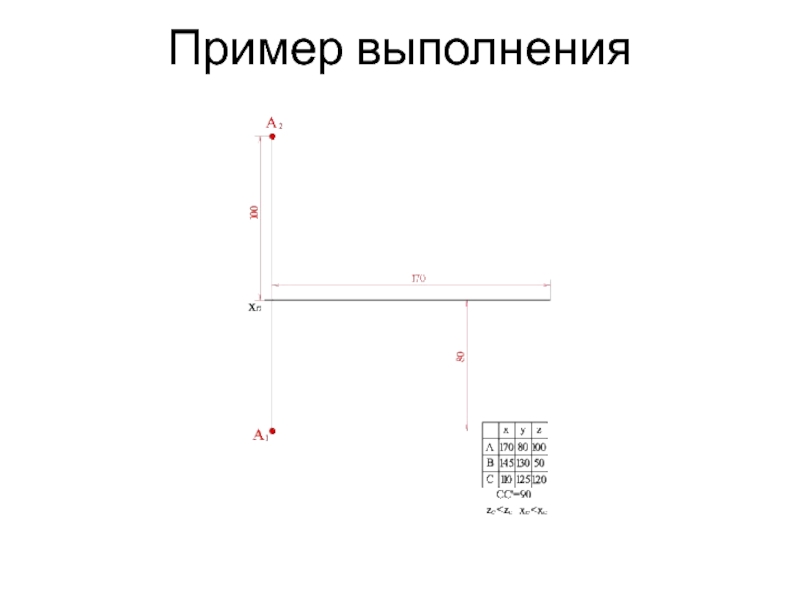
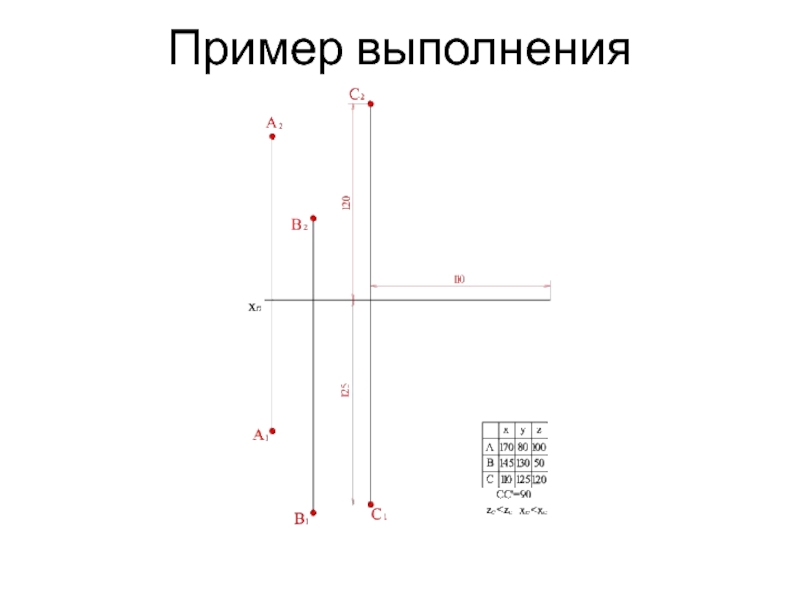
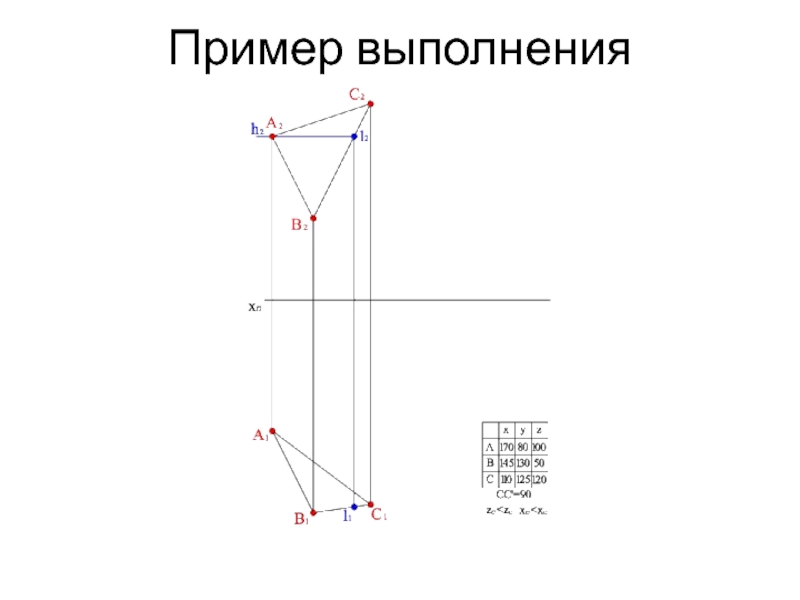
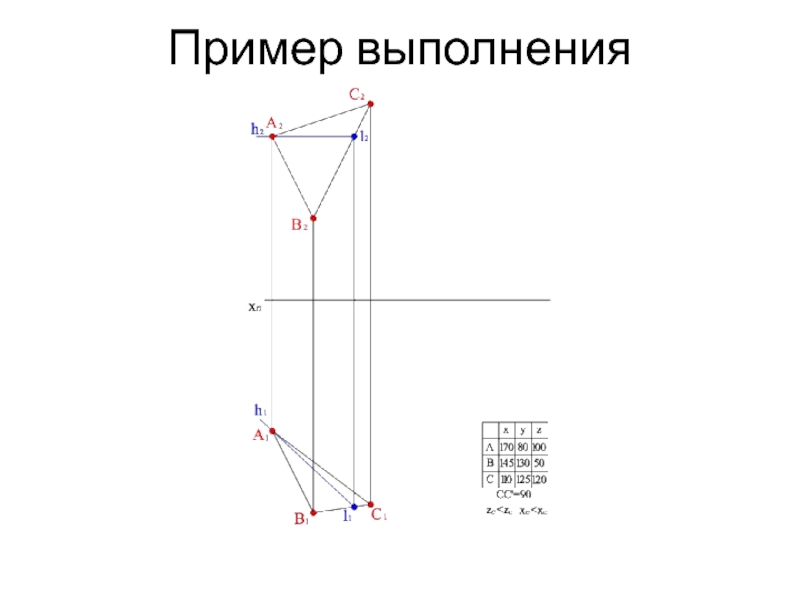
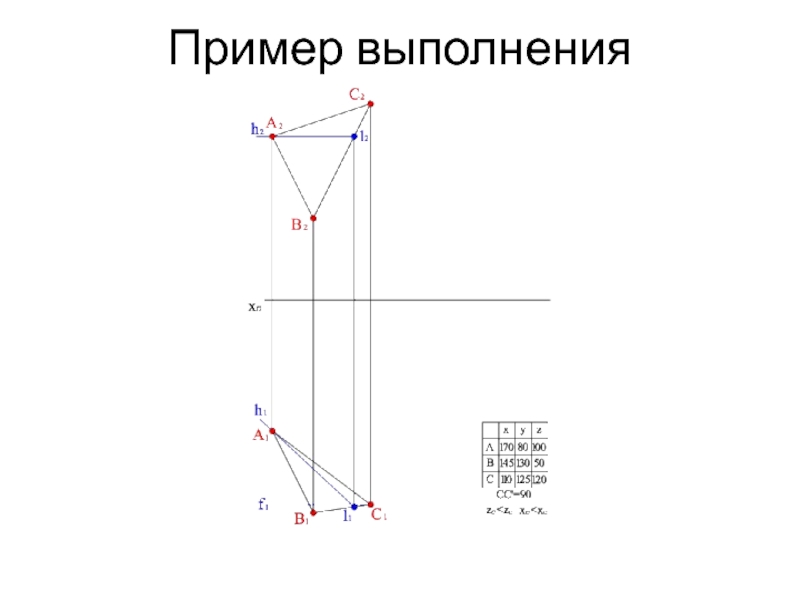
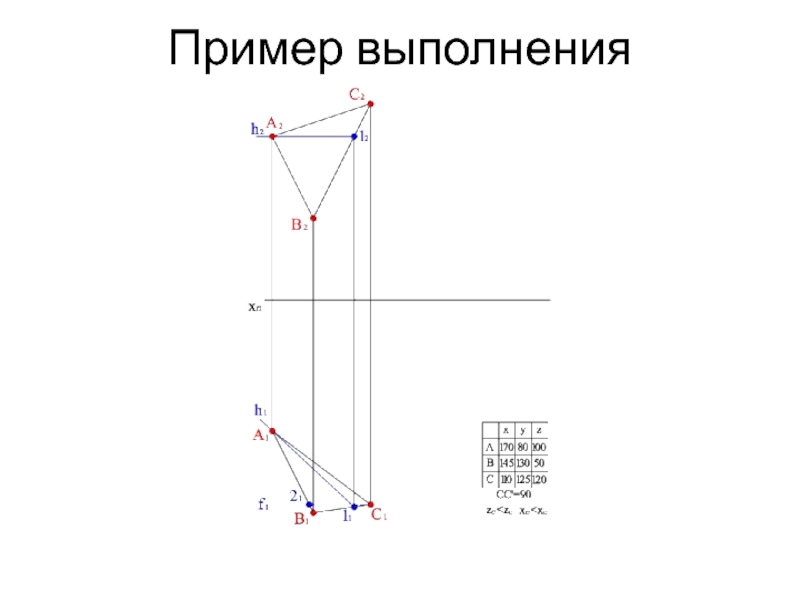
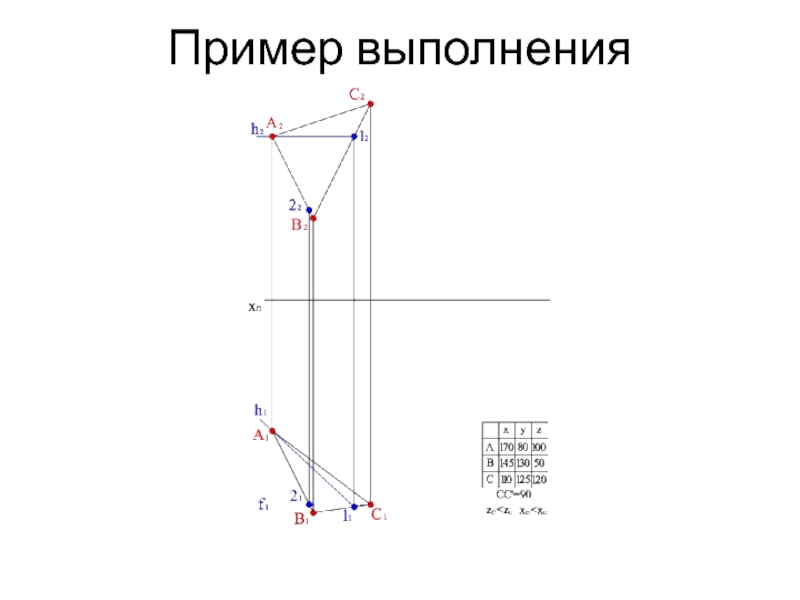
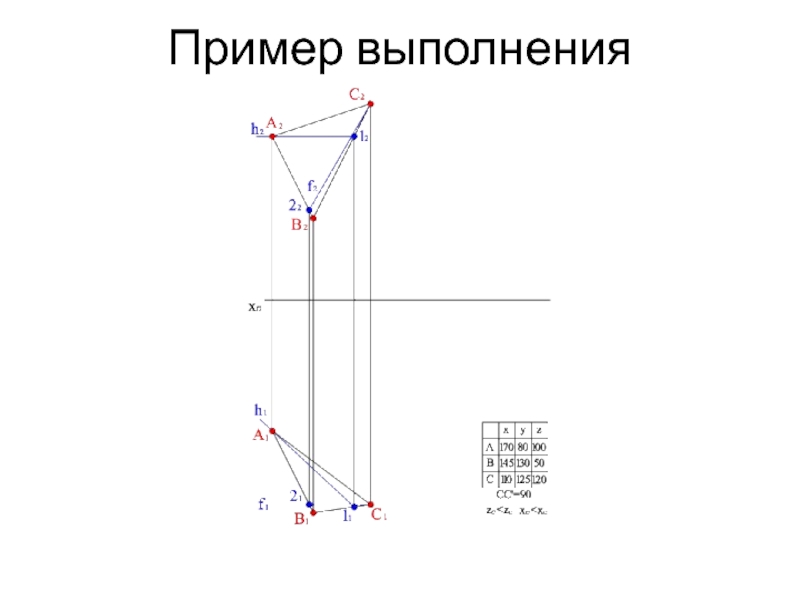
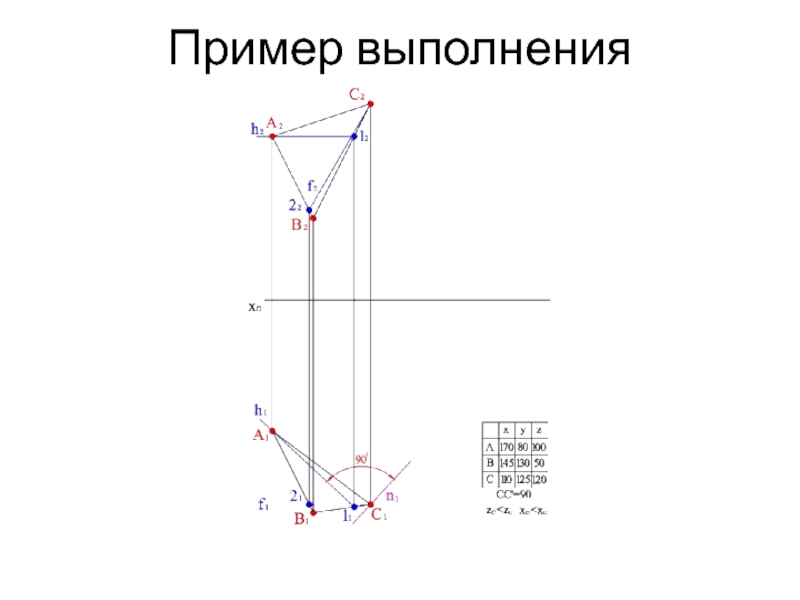
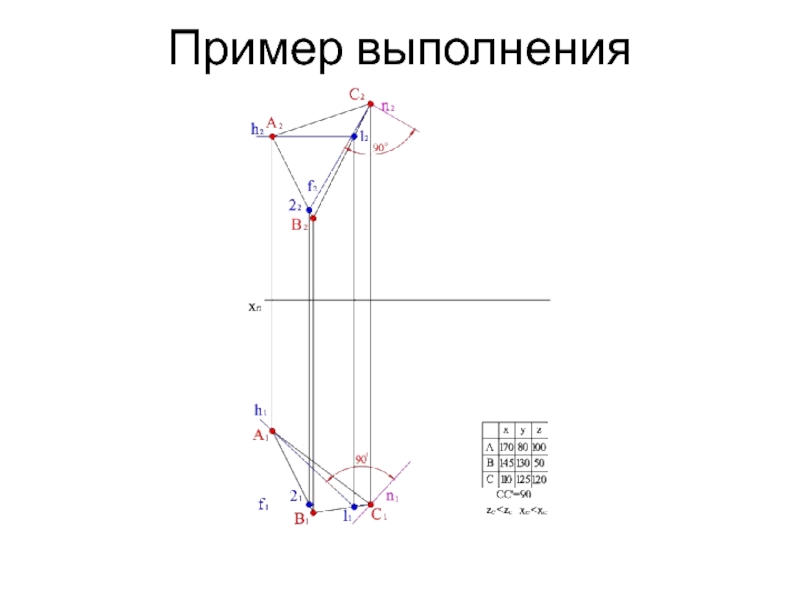
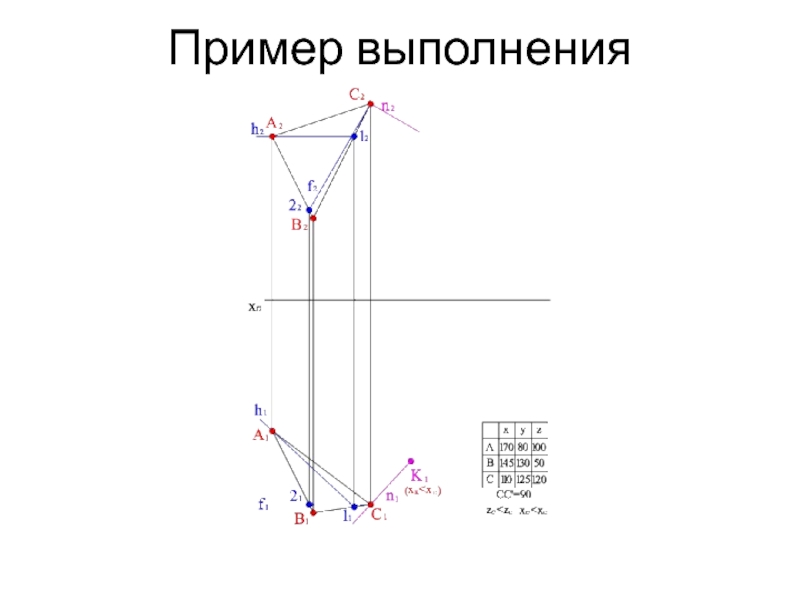
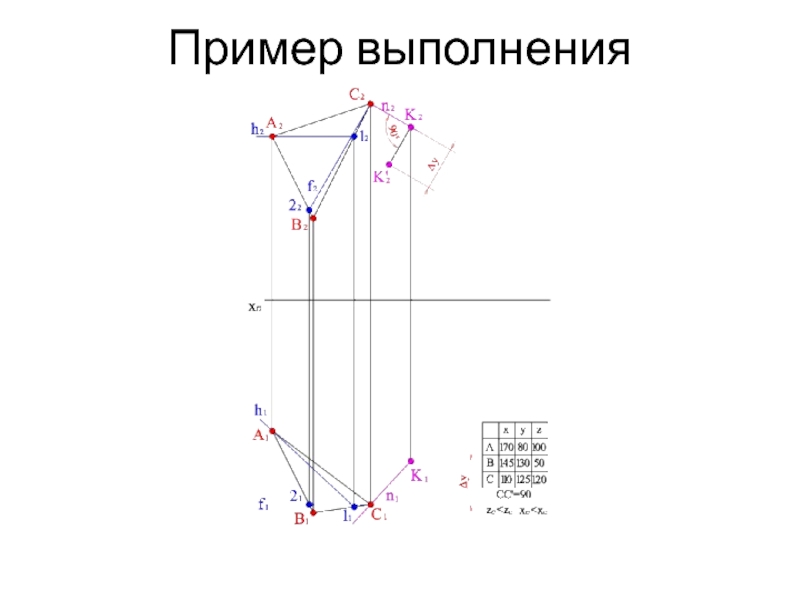
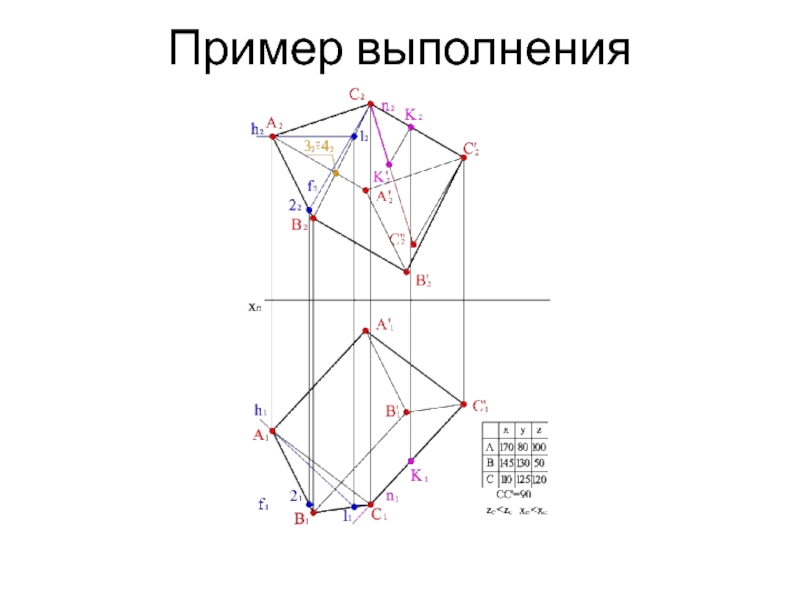
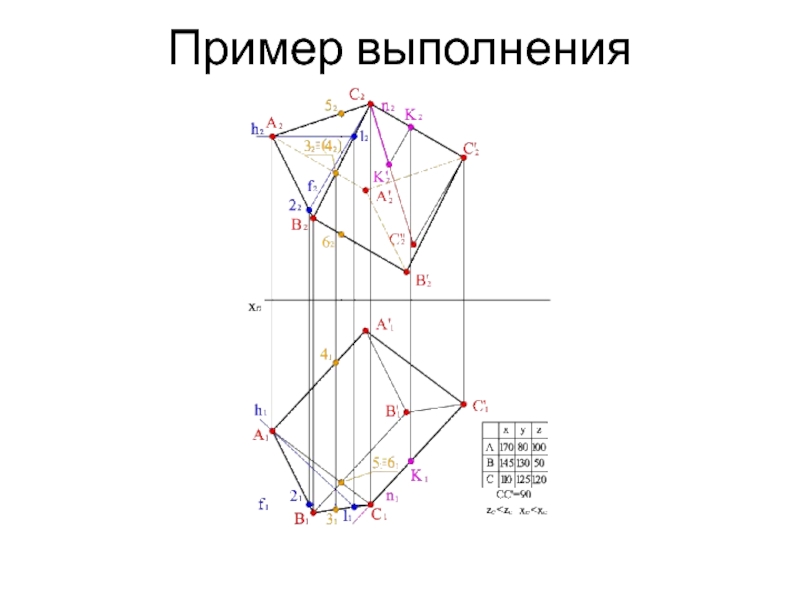
- 14. Пример выполнения
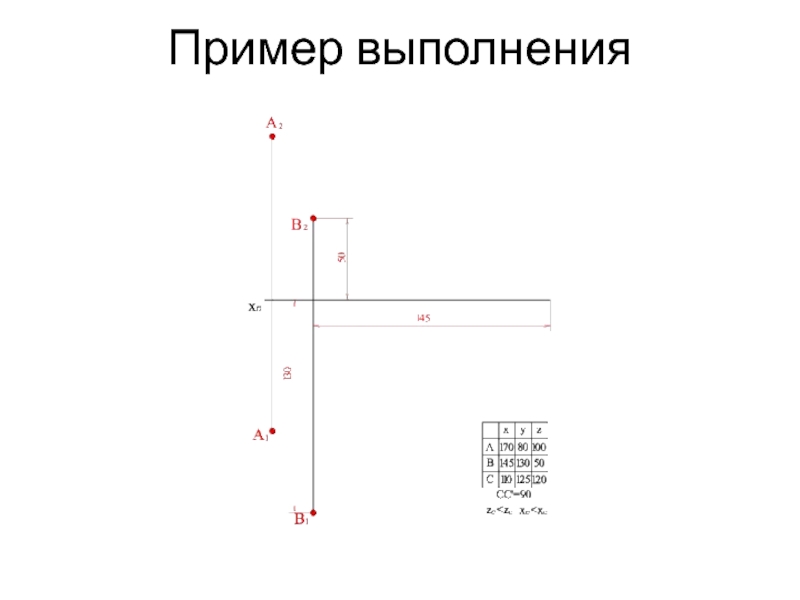
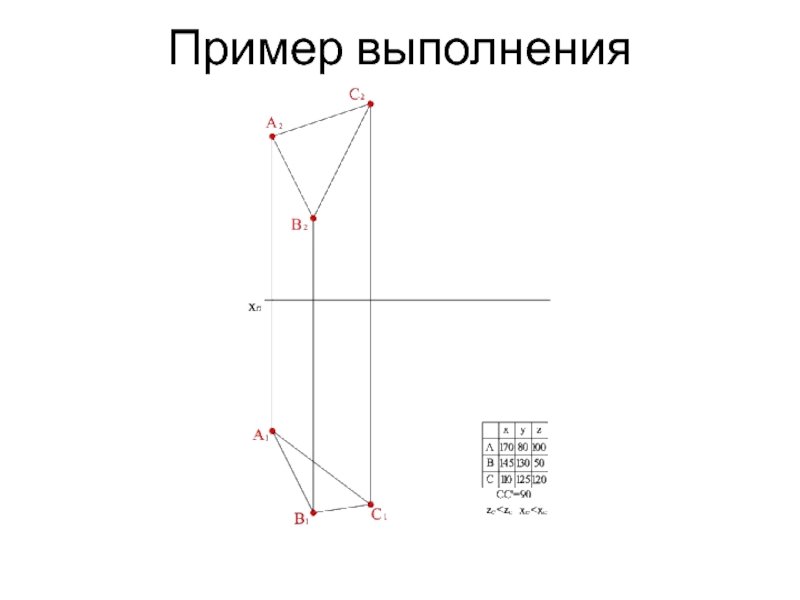
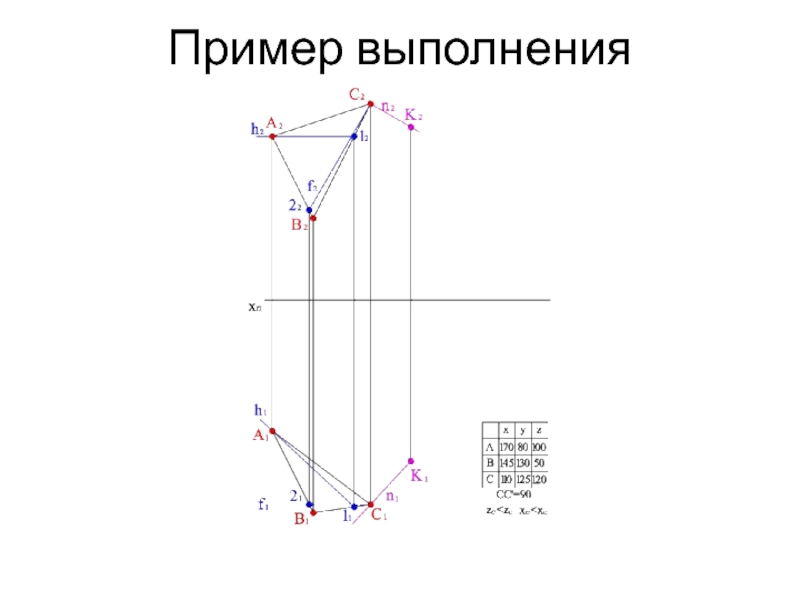
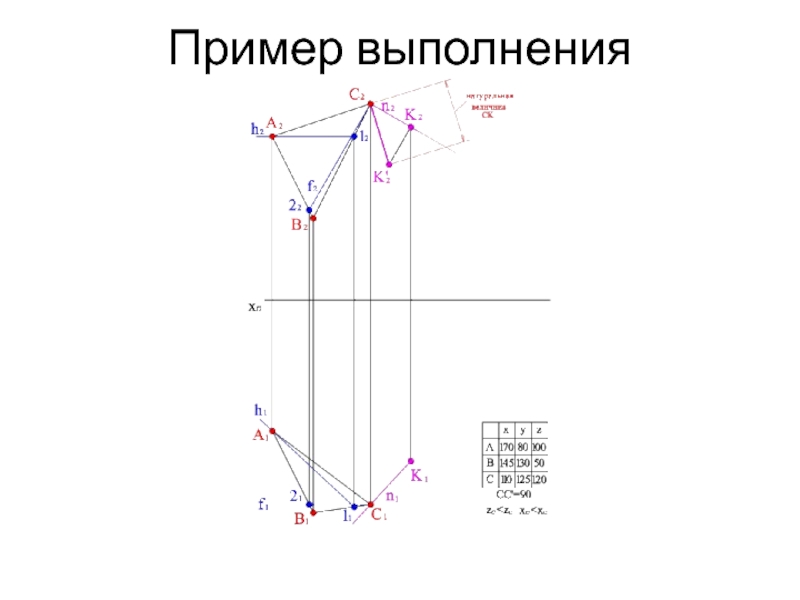
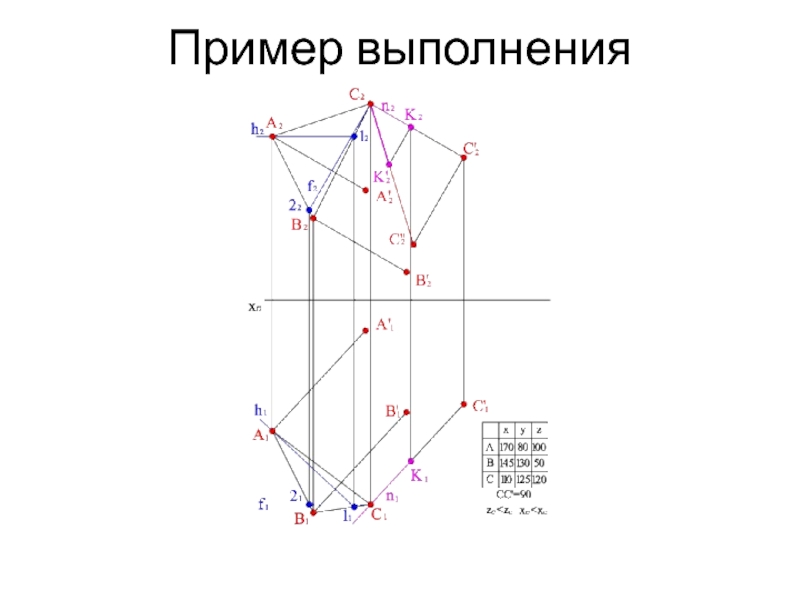
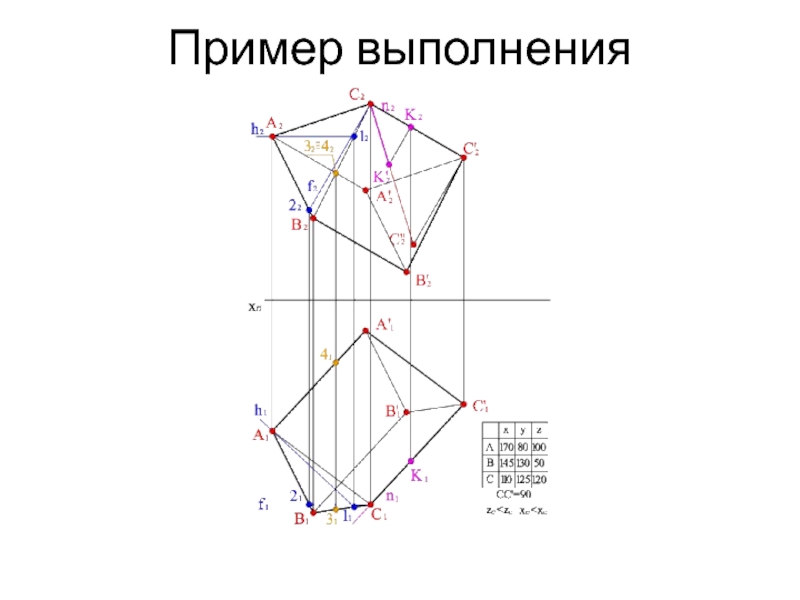
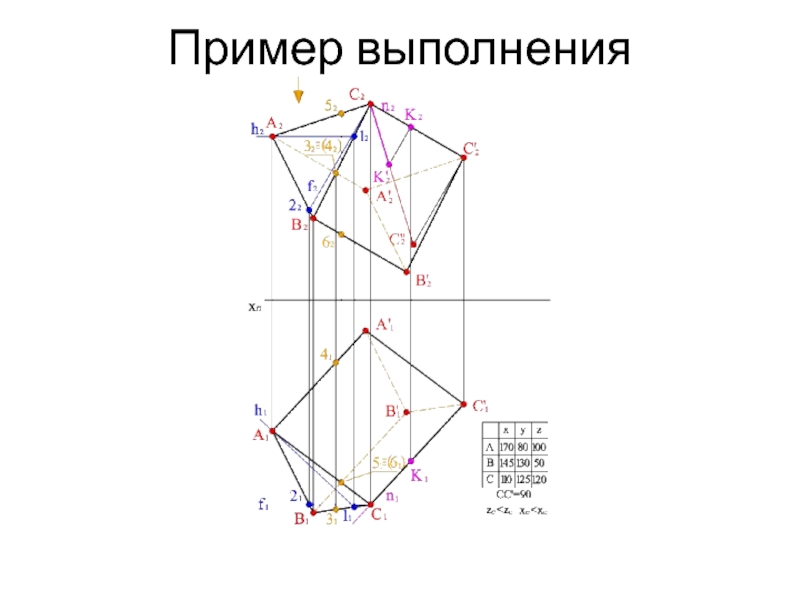
- 15. Пример выполнения
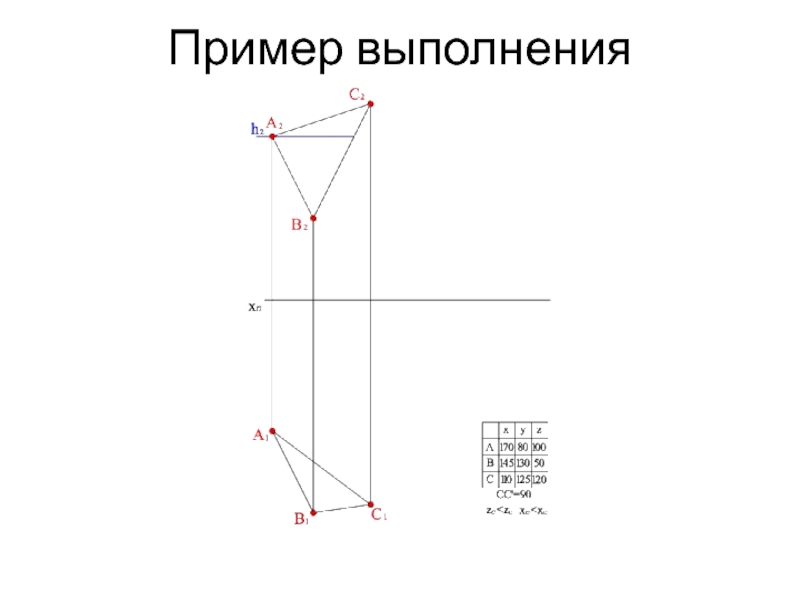
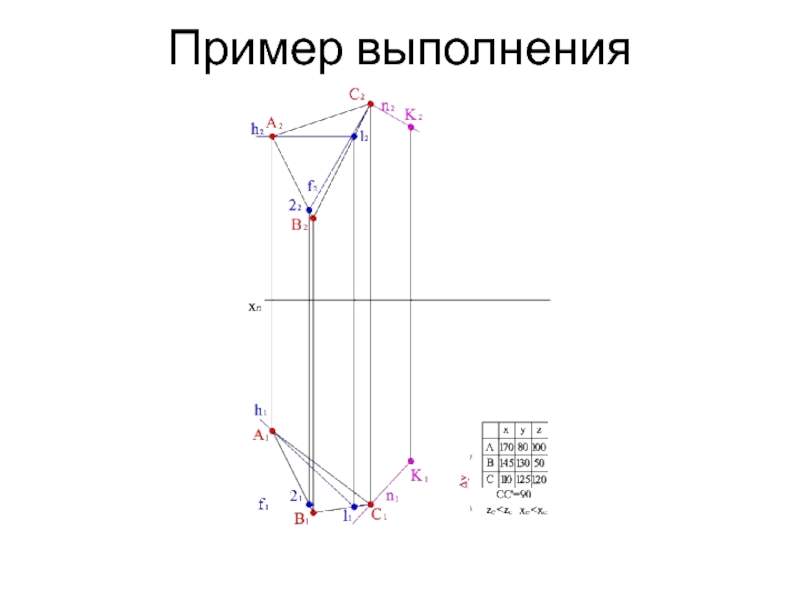
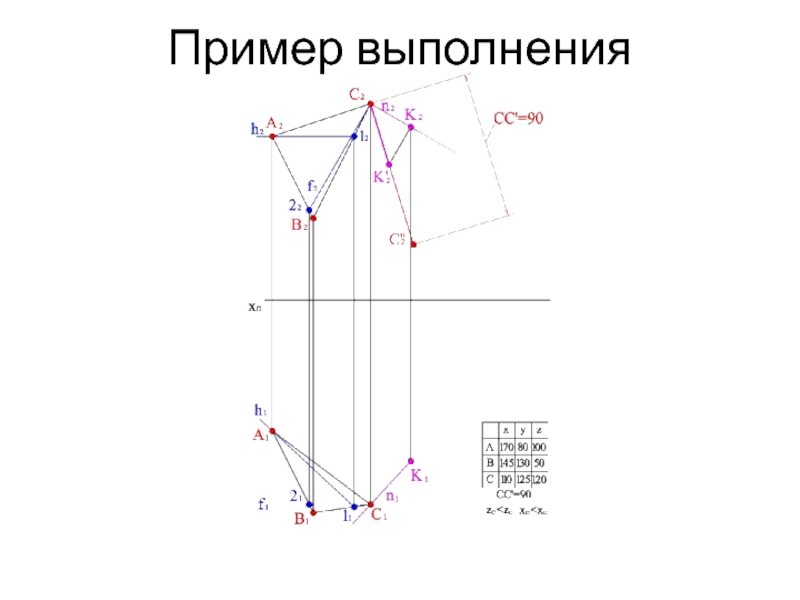
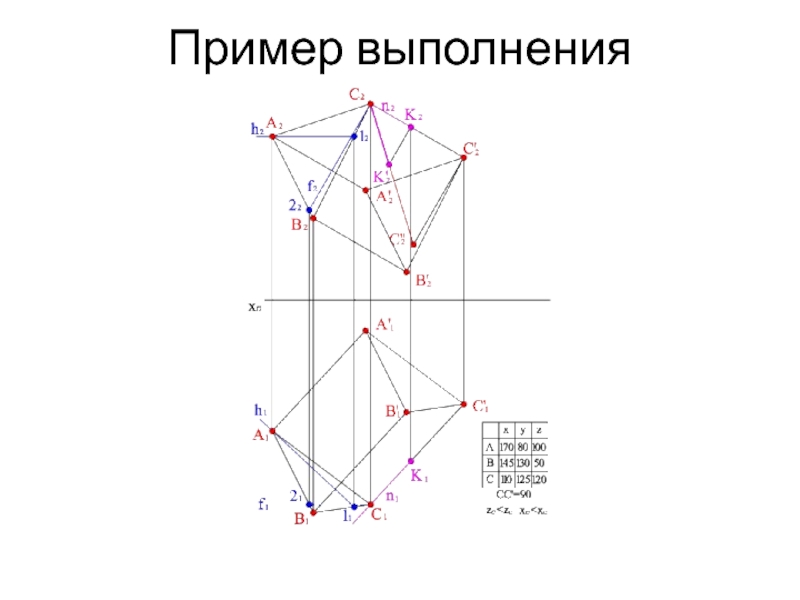
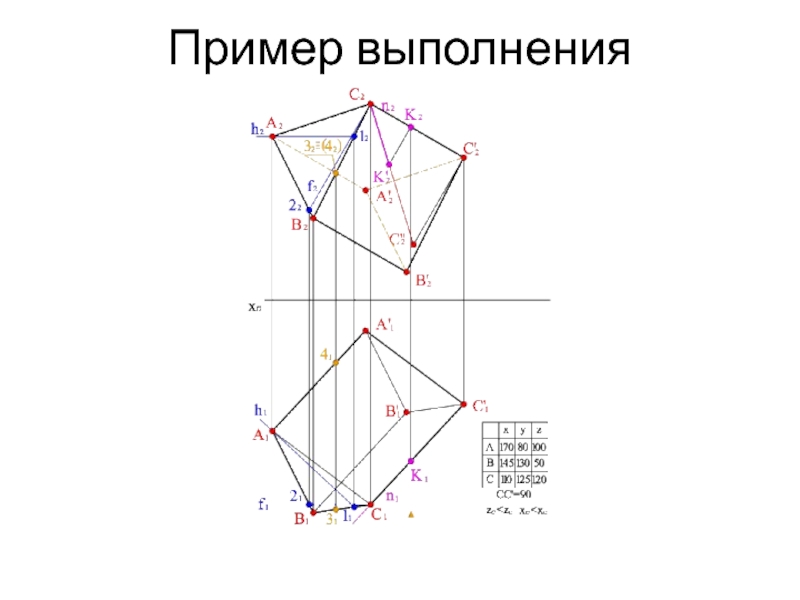
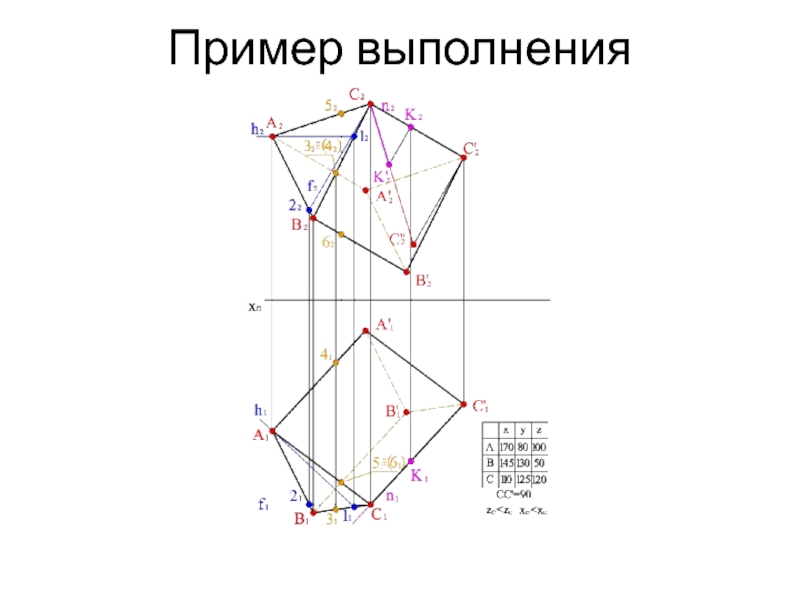
- 16. Пример выполнения
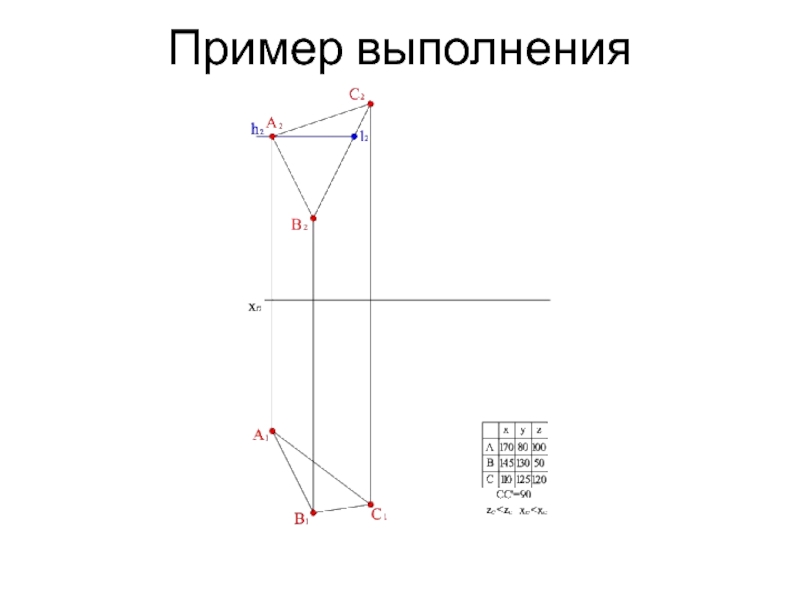
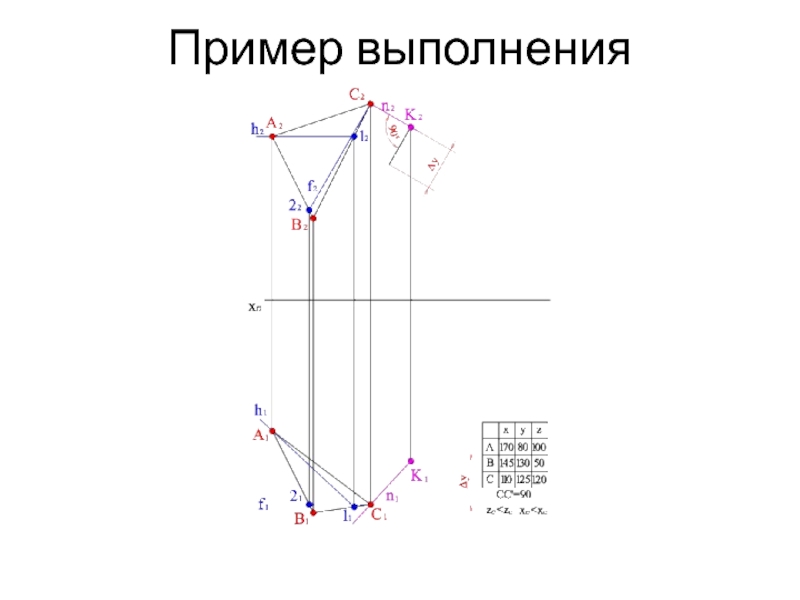
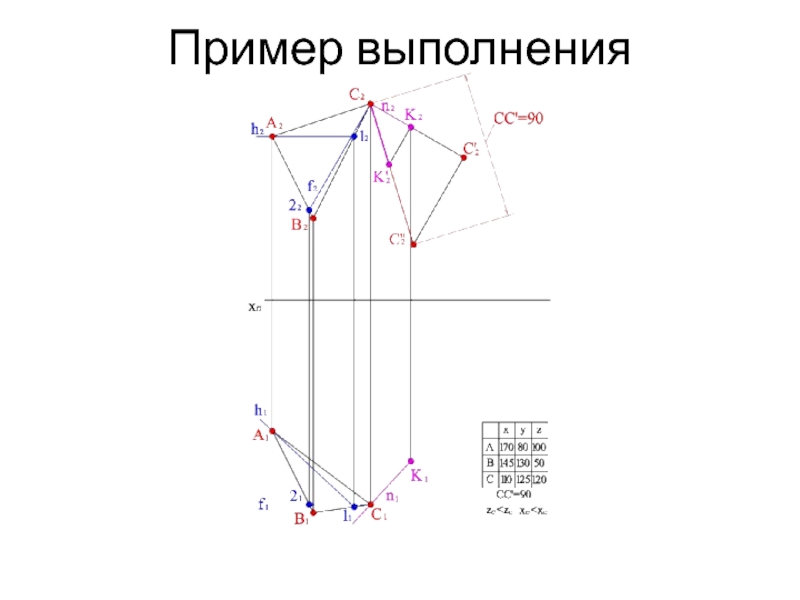
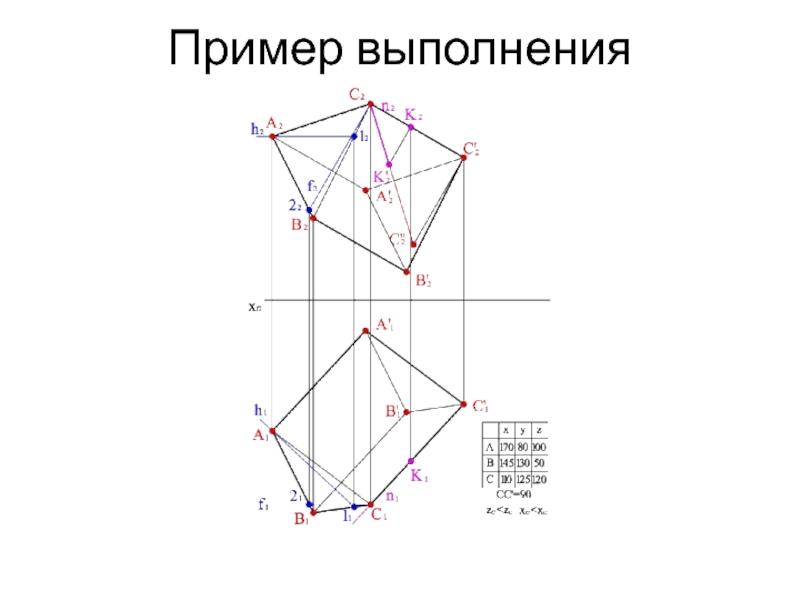
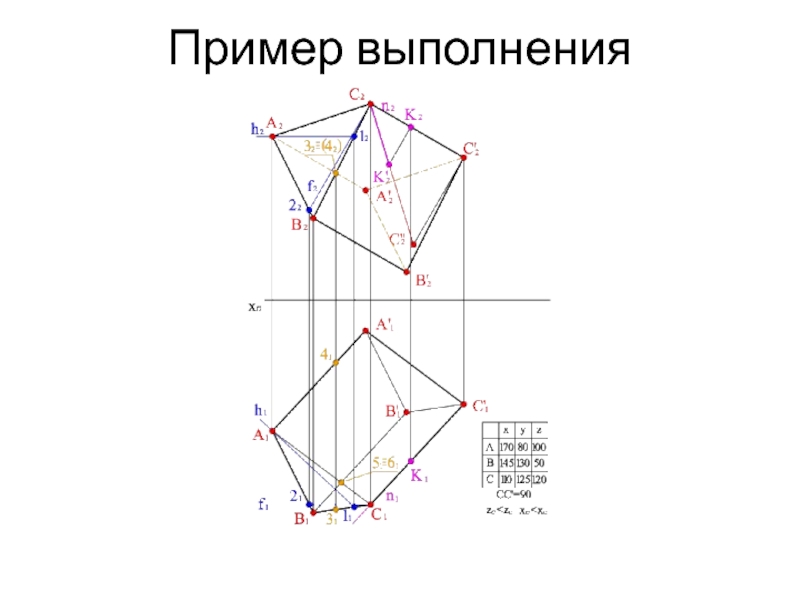
- 17. Пример выполнения
- 18. Пример выполнения
- 19. Пример выполнения
- 20. Пример выполнения
- 21. Пример выполнения
- 22. Пример выполнения
- 23. Пример выполнения
- 24. Пример выполнения
- 25. Пример выполнения
- 26. Пример выполнения
- 27. Пример выполнения
- 28. Пример выполнения
- 29. Пример выполнения
- 30. Пример выполнения
- 31. Пример выполнения
- 32. Пример выполнения
- 33. Пример выполнения
- 34. Пример выполнения
- 35. Пример выполнения
- 36. Пример выполнения
- 37. Пример выполнения
- 38. Пример выполнения
- 39. Пример выполнения
- 40. Пример выполнения
- 41. Пример выполнения
- 42. Пример выполнения
- 43. Пример выполнения
- 44. Пример выполнения
- 45. Пример выполнения
- 46. Пример выполнения
- 47. Пример выполнения
- 48. Пример выполнения
- 49. Скачать презентанцию
Многогранники
Слайды и текст этой презентации
Слайд 1САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
КАФЕДРА ПРИКЛАДНОЙ И КОМПЬЮТЕРНОЙ
ОПТИКИ
Слайд 3Многогранники
Многогранник в трехмерном пространстве - совокупность конечного числа плоских многоугольников
такая, что :
которых каждая сторона одного является одновременно стороной другого
(но только одного), называемого смежным с первым (по этой стороне);
2) от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого в свою очередь - к смежному с ним, и т.д.
Эти многоугольники называются гранями, их стороны ребрами, а их вершины - вершинами
многогранника.
Многогранник, полиэдр, - геометрическое тело, ограниченное со всех сторон плоскими
многоугольниками - гранями. Стороны граней называются ребрами, а концы ребер - вершинами.
По числу граней различают 4-гранники, 5-гранники и т.д.
Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой
его грани. Многогранник называется правильным, если его грани правильные многоугольники
(т.е. такие, у которых все стороны и углы равны) и все многогранные углы при вершинах равны.
Слайд 4Виды многогранников
Пирамида - это многогранник, одна грань которого многоугольник,
а остальные грани - треугольники с общей вершиной. Пирамида называется
правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостьюСлайд 5Виды многогранников
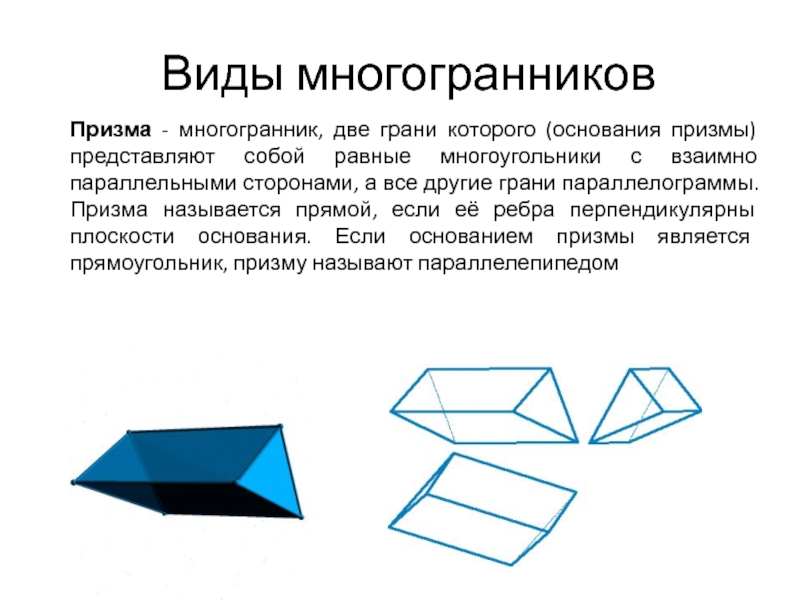
Призма - многогранник, две грани которого (основания призмы) представляют
собой равные многоугольники с взаимно параллельными сторонами, а все другие
грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедомСлайд 10Краткий экскурс в теорию Определение длины отрезка прямой линии и углов
наклона прямой к плоскостям проекций
(метод прямоугольного треугольника)
Слайд 11Метод прямоугольного треугольника
Длину отрезка АВ и a - угол наклона
отрезка к плоскости П1 можно определить из прямоугольного треугольника АВС
|AС|=|A1B1|, |BС|=DZ. Для этого на эпюре из точки B1 под углом 900 проводим отрезок |B1B1*|=DZ, полученный в результате построений отрезок A1B1* и будет натуральной величиной отрезка АВ, а угол B1A1B1*=a. Рассмотренный метод называется методом прямоугольноготреугольника.