Спектральные характеристики непериодических сигналов

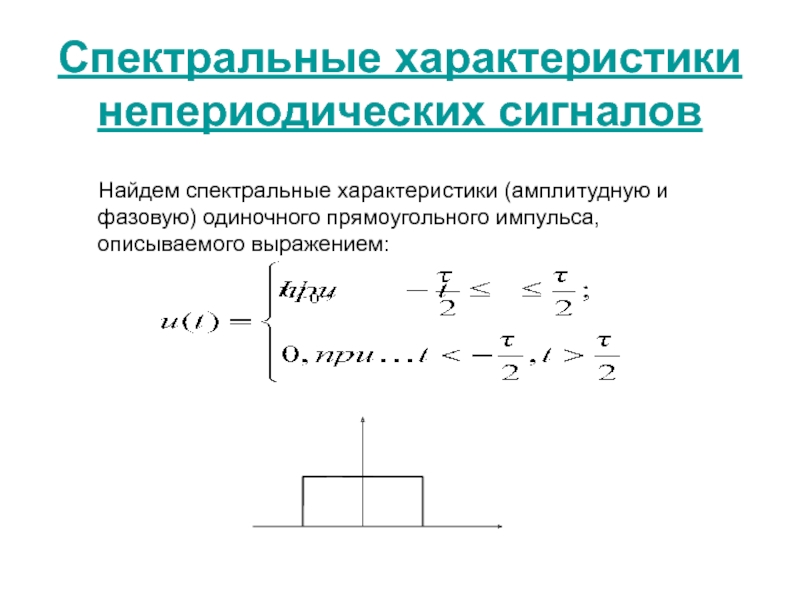
, отображающая реальный сигнал, абсолютно интегрируема,

то ее спектральная плотность определяется интегралом:


Величину называют комплексной спектральной плотностью или спектральной характеристикой. Она имеет размерность [амплитуда/частота]. Используя обратное преобразование Фурье для сигнала , можно записать:

величина, может быть записана в виде модуля и аргумента:


где модуль

называют спектральной плотностью амплитуд или просто амплитудным спектром непериодического сигнала, а аргумент спектральной плотности – фазовым спектром этого сигнала.

спектральной плотности могут быть вычислены по формулам:

, где




является четной функцией частоты, а – нечетной функцией частоты. Так как составляющие расположены на всех частотах, то спектр непериодического сигнала является непрерывным или сплошным.

Фурье нетрудно привести к тригонометрической форме:


Преимущество

тригонометрической формы записи Фурье-преобразования заключается в возможности некоторого физического толкования с использованием идеализаций, не очень далеких от реальности.

(амплитудную и фазовую) одиночного прямоугольного импульса, описываемого выражением:

Произведение , равное

площади импульса, определяет значение спектральной плотности импульса
при . Более того, это выражение справедливо для импульсов произвольной формы:

амплитуд) одиночного прямоугольного импульса описывается выражением:

Графически спектр амплитуд этого импульса представлен на рисунке (приведена правая часть спектральной характеристики, соответствующая положительным значениям ).

зависимости, характеризующей спектр амплитуд прямоугольного импульса, следует, что при увеличении

длительности импульса расстояние между нулями функции сокращается, что равносильно сужению спектра амплитуд. При этом значение возрастает.
При укорачивании (сжатии) импульса расстояние между нулями функции , напротив, увеличивается (спектр расширяется), а значение убывает.
В пределе при значение стремится к бесконечности, а модуль спектральной плотности, бесконечно малый по величине при постоянном значении , становится равномерным в полосе частот от до .

непериодического сигнала.
Рассмотрим импульсный сигнал

, физическим представлением которого будем считать электрическое напряжение на резисторе номиналом 1 Ом. Тогда энергия, выделяемая на этом резисторе, равна:


Выразим энергию через модуль спектральной характеристики этого сигнала . Для этого квадрат модуля запишем в виде:

После преобразований получим равенство Парсеваля.

Из него следует, что каждое из бесконечно малых

слагаемых , соответствующих бесконечно малым участкам спектра, характеризует энергию, приходящуюся на спектральные составляющие сигнала, сосредоточенные в полосе частот от до .
Равенство может быть записано в виде:


где - энергетический спектр сигнала.