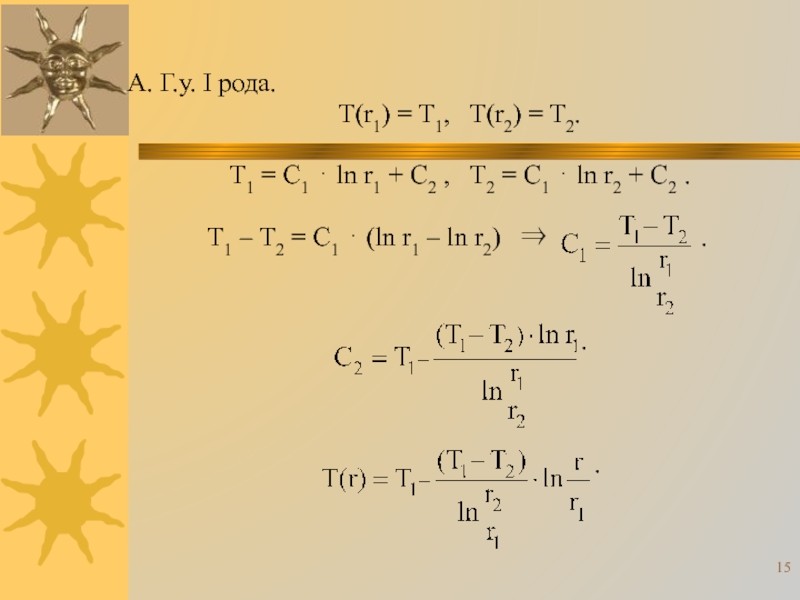Слайд 1Тема 4. Теплопроводность
Лекции 14, 15
Слайд 2§ 1. Основные положения
теории теплопроводности
Когда
не учитывают зависимость коэффициента теплопроводности от температуры, (или, что то же самое, используют среднее для данного температурного интервала значение ), то говорят о линейной теории теплопроводности.
Основной задачей теории теплопроводности является определение распределения температуры в объеме тела, поскольку согласно постулату Фурье, величина и направление теплового потока однозначно определяется температурным полем. Распределение температуры можно найти путем решения уравнения теплопроводности.
Слайд 3Поскольку для твердого тела конвективная производная температуры по времени равна
нулю, субстанциальная производная сводится к локальной:
, –
дифференциальное уравнение теплопроводности в декартовых координатах при отсутствии в объеме тела внутренних источников теплоты и при постоянном .
В § 3 было получено дифференциальное уравнение энергии для несжимаемой жидкости:
.
Слайд 4Линейное дифференциальное уравнение теплопроводности в цилиндрических координатах:
.
Наиболее общая форма уравнения теплопроводности для изотропного тела:
, –
дифференциальное уравнение теплопроводности в декартовых координатах при наличии внутренних источников теплоты и зависящем от температуры ,
Здесь с – объемная теплоемкость материала, Дж/(м3 К); qV – мощность внутренних источников теплоты, Вт/м3.
Слайд 5Чтобы из множества решений выбрать одно, соответствующее единичному явлению данного
класса, необходимо задать условия однозначности:
геометрические условия, определяющие форму
и размеры тела;
физические параметры материала , , с;
начальные условия, т.е. распределение температуры в объеме тела в начальный момент времени;
граничные условия, характеризующие тепловое взаимодействие окружающей среды с поверхностью тела.
Последние два типа условий объединяются термином «краевые условия».
Слайд 6Граничные условия (г.у.) можно задать разными способами:
А. Г.у. I рода
TW = TW (x, y, z, t), т.е. задается распределение
температуры по всей поверхности тела и изменение его во времени.
Б. Г.у. II рода qW = qW (x, y, z, t) = –
известна плотность теплового потока на поверхности и ее изменение во времени.
В. При г.у. III рода задается температура окружающей среды или внешнего источника (стока) теплоты T0 (x, y, z, t) и закон теплообмена между средой и поверхностью тела. То есть задается связь между известной температурой окружающей среды и неизвестной температурой поверхности тела (градиентом температуры на поверхности).
Слайд 7Стационарное линейное дифференциальное уравнение теплопроводности в декартовых координатах при отсутствии
внутренних источников теплоты имеет вид:
.
Для задач стационарной теплопроводности начальные условия не имеют смысла, задают лишь граничные условия.
Рассмотрим бесконечную пластину, имеющую конечную толщину вдоль оси х. Уравнение принимает вид:
.
§ 2. Стационарная теплопроводность в неограниченной пластине (тепловые потери через стены печей)
Слайд 8Интегрируя один раз, получим:
.
Вторично интегрируя, получим:
Т(х) = С1 х + С2 .
А. Г.у. I рода.
Расположив начало координат на одной из поверхностей, имеем:
Т(0) = Т1, Т() = Т2 .
Следовательно,
С2 = Т1, .
.
,
где – внутреннее тепловое сопротивление.
Б. Г.у. II рода.
qW(0) = qW () = q = const.
.
Константа С2 может принимать любые значения. Для нахождения С2 необходимо задать ТW(0) (ТW ()) либо Т0 и с любой стороны.
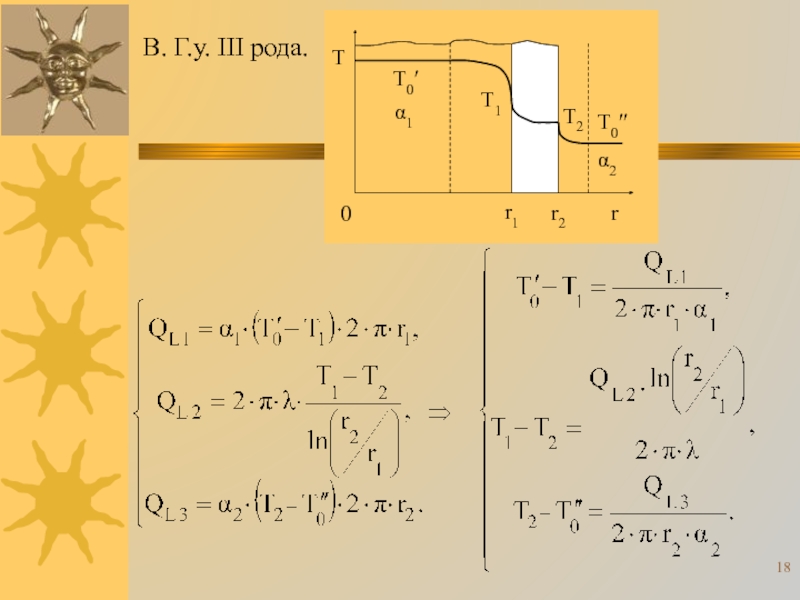
Слайд 10В. Г.у. III рода.
Рассмотрим случай конвективной теплоотдачи:
Дано:
,
1, 2.
Ввиду стационарности процесса q1 = q2
= q3 = q .
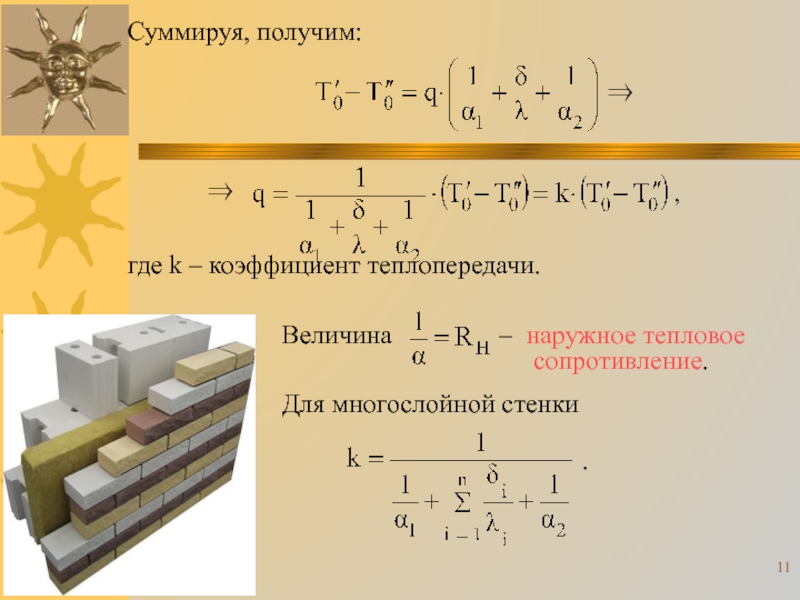
Слайд 11Величина – наружное
тепловое сопротивление.
Суммируя, получим:
,
где k – коэффициент теплопередачи.
Для многослойной стенки
.
Слайд 12 Многослойные теплоизоляционные системы в строительстве:
А – утеплитель – внутри ограждающей
конструкции (ISOVER);
Б – система «мокрого» типа («Опытный завод сухих
смесей»);
В – вентилируемый фасад (PAROC).
Слайд 13§ 3. Стационарная теплопроводность
в цилиндрической стенке
(изоляция трубопроводов)
Для цилиндрической стенки, неограниченно простирающейся вдоль
оси х, в осесимметричном случае, (т.е. при неизменных по граничным поверхностям стенки условиям) уравнение теплопроводности принимает вид:
.
Используя подстановку , получим уравнение
с разделяющимися переменными:
.
Слайд 14Интегрируя, имеем:
ln u + ln r = ln C1 .
После
потенцирования получаем:
u r = C1 .
Переходя к
переменной Т и выполняя разделение переменных, имеем уравнение:
,
интегрируя которое, находим искомое решение:
Т(r) = С1 ln r + С2 .
.
Слайд 15А. Г.у. I рода.
T(r1) = T1, T(r2) = T2.
Т1
= С1 ln r1 + С2 , Т2
= С1 ln r2 + С2 .
Т1 – Т2 = С1 (ln r1 – ln r2) .
.
.
Слайд 16Плотность теплового потока, проходящего через
любую цилиндрическую поверхность внутри стенки
с текущим радиусом r:
,
откуда тепловой поток, проходящий через трубу длиной L, получается постоянным по толщине и равным, Вт:
.
Слайд 17Тепловой поток, проходящий через цилиндрическую стенку единичной длины, называется линейной
плотностью теплового потока, Вт/м:
,
где RL ВН – внутреннее линейное тепловое сопротивление цилиндрической стенки.
.
Б. Г.у. II рода.
Как и для плоской стенки, задача не имеет единственного решения.
Слайд 19Для сохранения стационарного режима необходимо, чтобы
QL 1 = QL 2
= QL 3 = QL .
Суммируя уравнения системы, получим:
.
где kL – линейный коэффициент теплопередачи.
– наружное линейное тепловое сопротивление.
При
теплопередаче через многослойную стенку
,
Зная и определив QL, можно найти Т1, Т2 и Т(r).
Слайд 21Рассмотрим влияние наружного диаметра однородной цилиндрической стенки на ее суммарное
линейное тепловое сопротивление.
.
Считаем, что d1 = const, тогда при увеличении наружного диаметра d2 увеличивается внутреннее линейное тепловое сопротивление
,
а наружное
–
уменьшается.
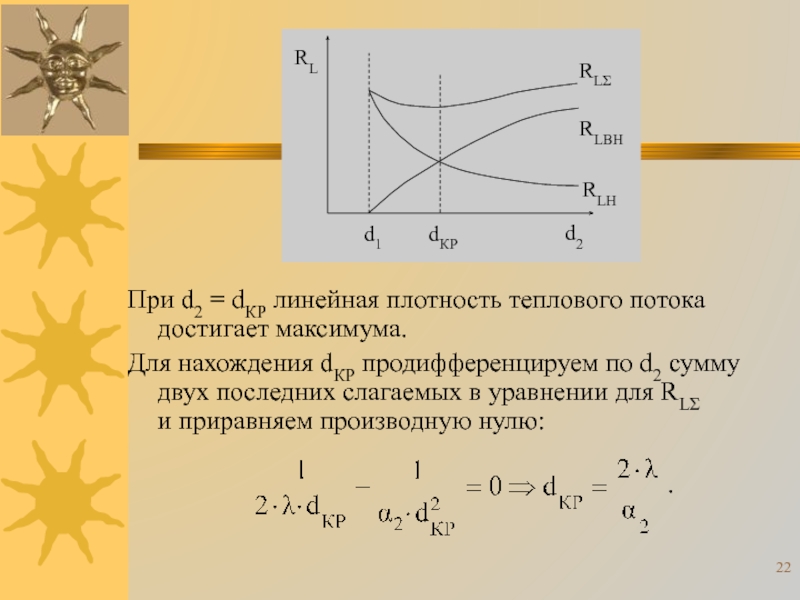
Слайд 22При d2 = dКР линейная плотность теплового потока достигает максимума.
Для
нахождения dКР продифференцируем по d2 сумму двух последних слагаемых в
уравнении для RLΣ и приравняем производную нулю:
.