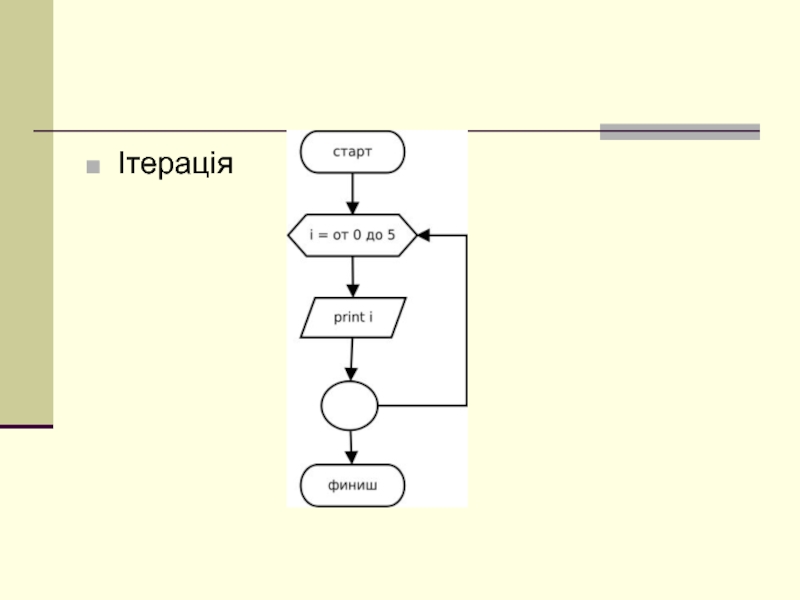
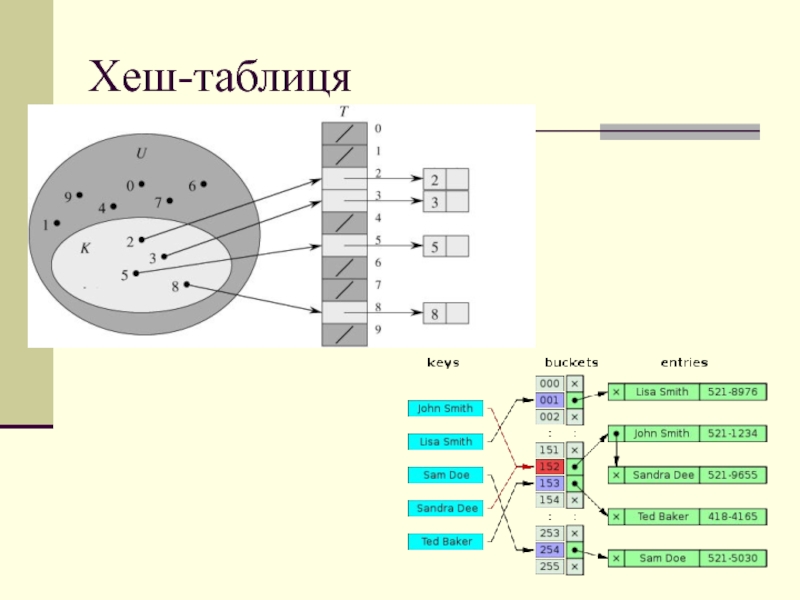
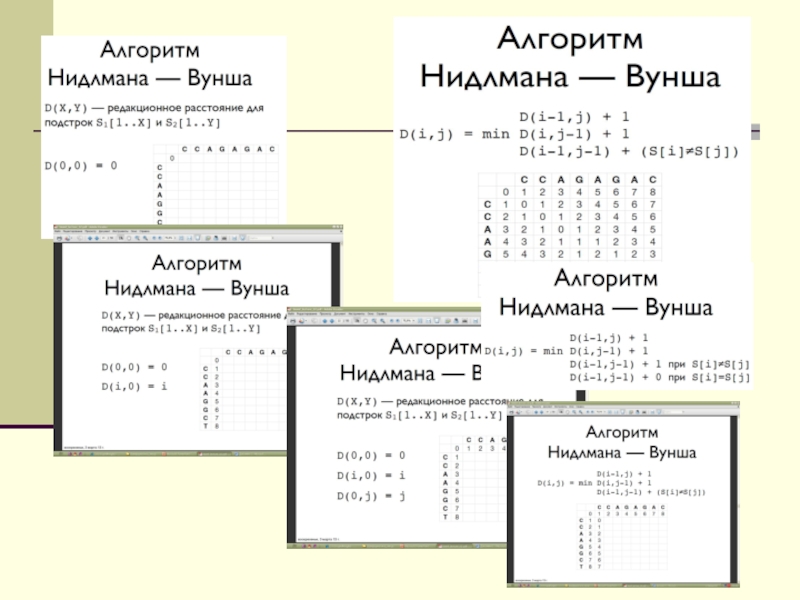
Слайд 1Тема: Вирівнювання послідовностей
Слайд 2План:
Типи вирівнювань послідовностей;
Методи вирівнювання;
Алгоритми розпізнавання доменів у білкових структурах.
Слайд 3Література:
Игнасимуту С. Основы биоинформатики. – М. – Ижевск: НИЦ «Регулярная
и хаотическая динамика», Институт компьютерных исследований, 2007. – 320 с.
Гриценко
В.І., Котова А.Б., Вовк М.І. та ін.Інформаційні технології в біології та медицині. Навчальний посібник. – Київ: Наукова думка, 2007. – 381 с.
David W.Moumt. «Bioinformatics», 2006. – 565 p.
Слайд 4Інформаційні ресурси:
http://www.bioinformatix.ru
http://www.matbio.org
http://bioinformatics.ru
Слайд 5
Попарне вирівнювання
augaguucucuaaagcuccagaagaggcucgcagccuccgugcugcgaugcggcaagaag
aaggucugguuggaucccaaugaaaucaacgagaucgcuaacacaaacucgcgucagaac
Множинне вирівнювання
Слайд 7Типи вирівнювань:
Глобальне
Локальное
Слайд 8Попарне вирівнювання – вставка проміжків
AKWTNLK----WAKV-ADVAGH-G
AK-TNVKAKLPWGKVGAHVAGEYG
- вставка\видалення проміжка
- видовження проміжка
Слайд 9Для аналізу порівняння обраховують:
Відсоток ідентичності;
Відсоток схожості.
Слайд 10Попарне вирівнювання
Людський гемоглобін (HH):
VLSPADKTNVKAAWGKVGAHAGYEG
Міоглобін кашалота (SWM):
VLSEGEWQLVLHVWAKVEADVAGHG
Слайд 11Попарне вирівнювання - ідентичність
(HH) VLSPADKTNVKAAWGKVGAHAGYEG
||| |
| || | |
(SWM) VLSEGEWQLVLHVWAKVEADVAGHG
Відсоток ідентичності:
36 %
Слайд 12Попарне вирівнювання - схожість
(HH) VLSPADKTNVKAAWGKVGAHAGYEG
||| . |
| || | |
(SWM) VLSEGEWQLVLHVWAKVEADVAGHG
Відсоток схожості: 40
%
Відсоток ідентичності: 36 %
Слайд 13Попарне вирівнювання – вставка проміжків (gaps)
(HH) VLSPADKTNVKAAWGKVGAH-AGYEG
.
(SWM) VLSEGEWQLVLHVWAKVEADVAGH-G
Gaps:
2
Відсоток схожості: 56
Відсоток ідентичності: 44
Слайд 14Попарне вирівнювання - підрахунок
Фінальна оцінка вирівнювання – це сума сум
позитивних балів і штрафних балів:
+ Кількість ідентичних
+ Кількість схожих
- Кількість
вставлених проміжків
- Кількість видовжених проміжків
Оцінка вирівнювання
Слайд 15Які задачі розв'язує вирівнювання?
Нуклеотиди
Вивчення еволюційних зв'язків.
Пошук генів, доменів, сигналів …
Білки
Вивчення еволюційних зв'язків.
Класифікація білкових сімейств за функцією або структурою.
Ідентифікація загальних
доменів за функцією або структурою.
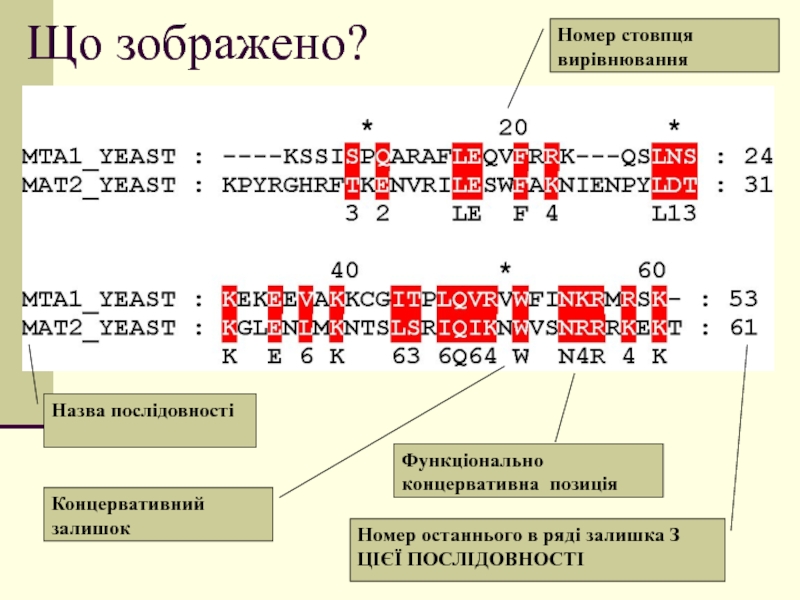
Слайд 16Що зображено?
Назва послідовності
Номер стовпця вирівнювання
Номер останнього в ряді залишка З
ЦІЄЇ ПОСЛІДОВНОСТІ
Концервативний залишок
Функціонально концервативна позиція
Слайд 17Види матриць:
Матриці ВТМ (відсотка точкових мутацій,
PAM).
Матриці БЛОЗАМ (блокових замін).
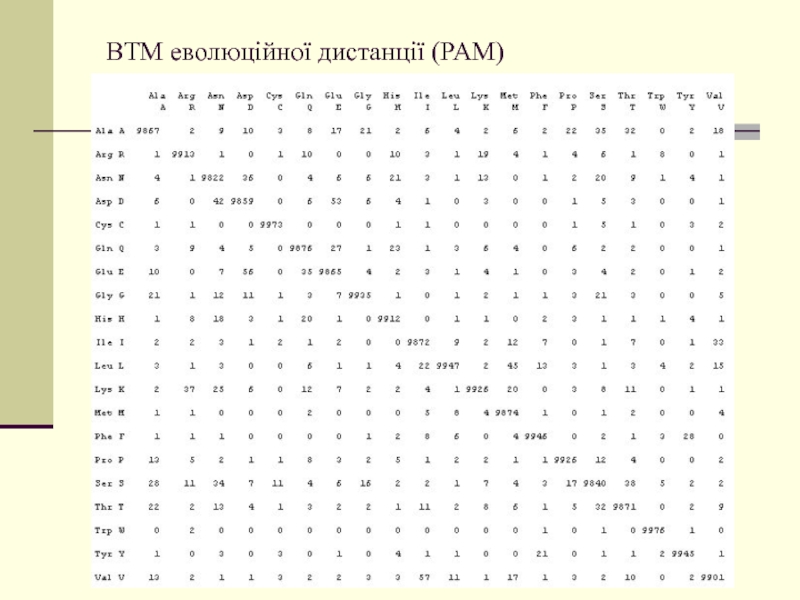
Слайд 18 ВТМ еволюційної дистанції (PAM)
Слайд 21Методи для попарного вирівнювання:
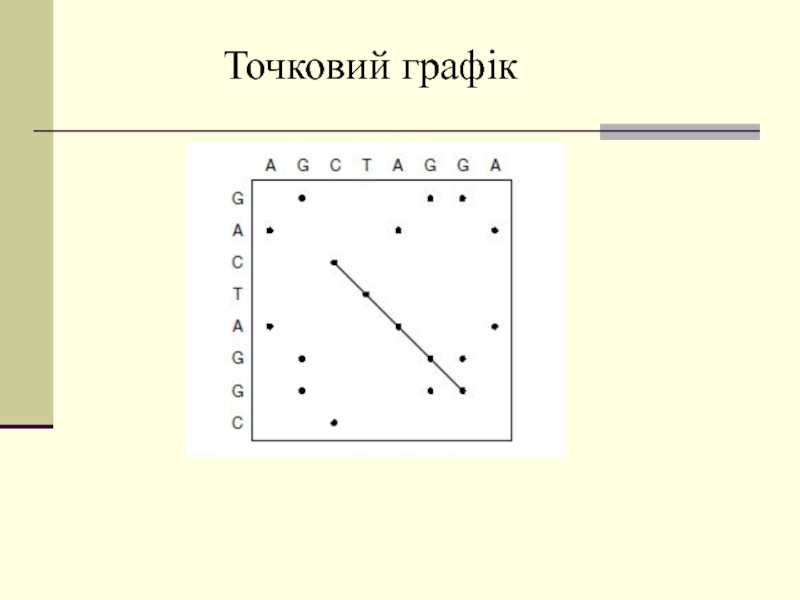
Точковий графік;
Динамічне програмування;
Метод “слів”, або k-кортежів.
Слайд 23Точкова матриця (співпадіння між коротким і повним іменами)
Слайд 24Точкова матриця (співпадіння повторюваної послідовності з самою собою (ABRACADA
BRACADABRA)
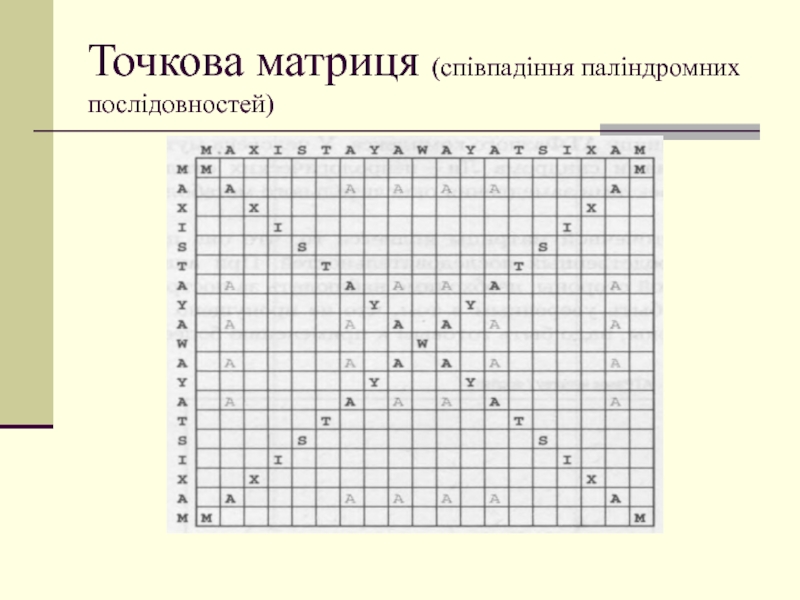
Слайд 25Точкова матриця (співпадіння паліндромних послідовностей)
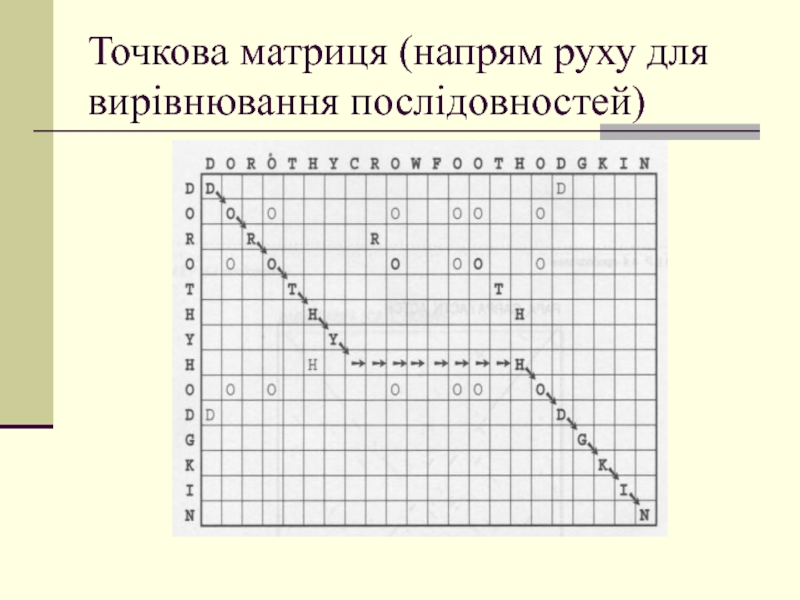
Слайд 26Точкова матриця (напрям руху для вирівнювання послідовностей)
Слайд 27Динамічне програмування
Послідовність Фібоначчі, числа Фібоначчі — числова послідовність задана
рекурентним співвідношенням другого порядку
Слайд 28
Окремі операції редагування включають в себе:
Заміна bj на ai відображається записом (ai,bj);
Делеція ai з послідовності А відображається записом (ai,Ø);
Делеція bj з послідовності В відображається записом (Ø, bj).
Слайд 29Функція ваги d:
d(ai,bj) = ціна мутації у вирівнюванні, де позиція
і послідовності А відповідає позиції j послідовності В, і мутація
проводить заміну ai↔bj, d(ai,Ø) або d(Ø, bj) = ціна делеції або вставки.
Слайд 30Відстань мінімальної ваги між послідовностями А і В:
D(A,B)=min∑d(x,y)
A→B
де х,у Є А+ і мінімум
береться з усієї послідовності операції редагування, які перетворюють А і В в загальну послідовність.
Слайд 31Значення D(i,j) відповідає перетворенню першопочаткових послідовностей Аi=а1а2…аi і
Вj=b1 b2… bj в загальну послідовність шляхом L операцій
редагування Sk, k=1, …, L, які можуть бути розглянуті в порядку зростання позицій в рядках.
Слайд 32Відміна останньої операції редагування:
Утворена в результаті вкорочена послідовність операцій редагування
Sk, k=1, …, L-1, являє собою послідовність операцій конвертування підрядка
Аi і підрядка Вj в загальний результат.
Слайд 33Відповідність між індивідуальними операціями редагування і кроками між суміжними комірками
матриці:
(i-1, j-1) → (i, j) відповідає заміні аi → bj
.
(i-1, j) → (i, j) відповідає делеції аi з А.
(i, j-1) → (i, j) відповідає вставці bj в А в позицію i.
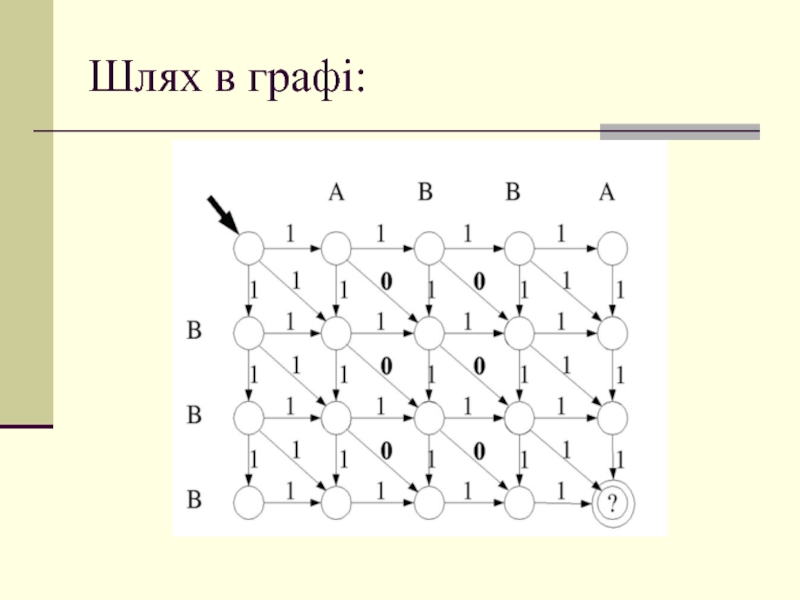
Слайд 34Послідовності операцій редагування відповідають сходинчастому шляху по матриці
(io, jo) =
(0, 0) → (i1, j1) → … (n, m)
де 0
≤ ik+1-ik ≤ 1, (для 0 ≤ k ≤ n-1),
0 ≤ jk+1- jk ≤ 1, (для 0 ≤ k ≤ m -1).
Слайд 35Отже, кінцевий алгоритм:
Обрахувати матрицю D розміром (m+1)x(n+1), застосовуючи: 1) початкові
умови на верхній ряд і ліву колонку
і
D(i, 0)=∑d(ak, Ø)
k=0
j
D(0, j)=∑d(Ø, bk)
k=0
Слайд 362) рекурентні співвідношення:
D(i, j)= min {D(i-1, j)+d(ai,Ø), D(i-1, j-1)+d(ai,bj), D(i,
j-1)+d(Ø, bj)}
де i=1, …, n; j=1, …, m.
Слайд 37Це означає, що ми враховуємо всі три можливих кроки для
D(i, j):
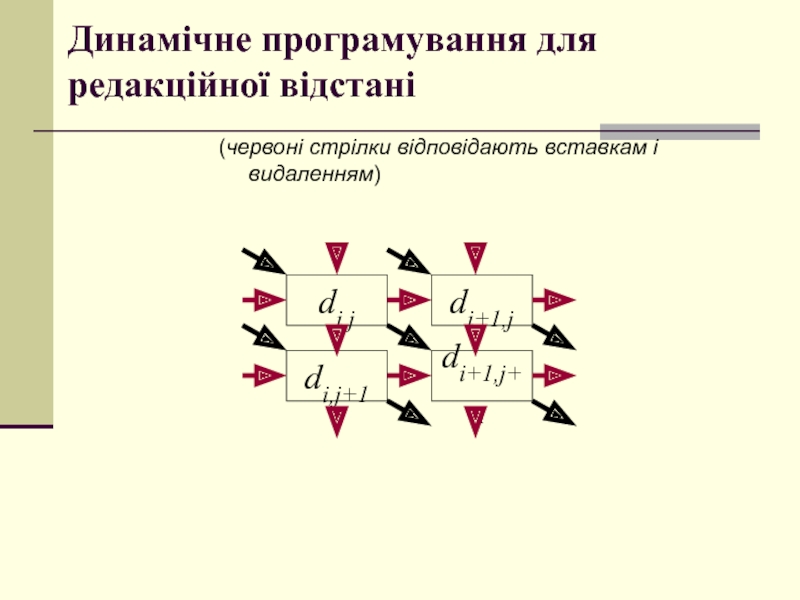
Слайд 38Динамічне програмування для редакційної відстані
(червоні стрілки відповідають вставкам і видаленням)
di,j
di+1,j
di,j+1
di+1,j+1
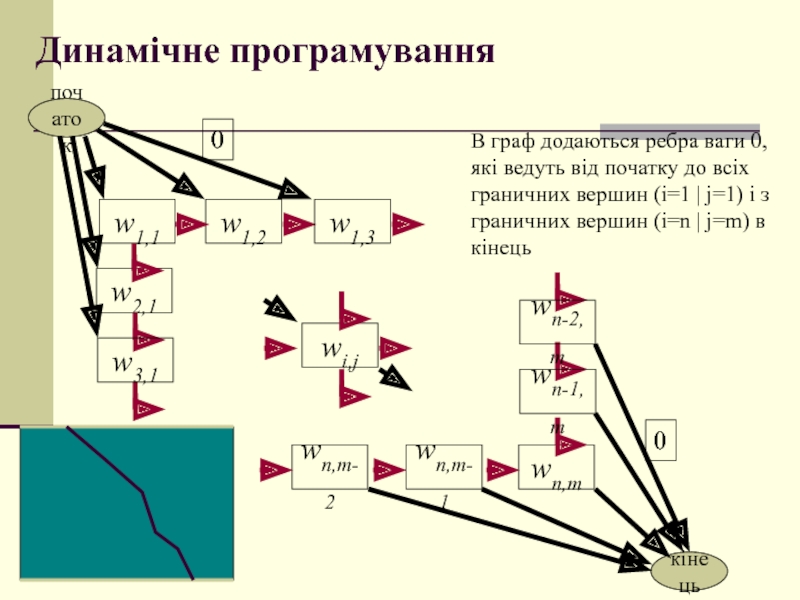
Слайд 39Динамічне програмування
wi,j
w1,1
початок
w1,2
w2,1
wn,m-1
wn,m
w3,1
wn-1,m
кінець
wn,m-2
wn-2,m
w1,3
0
0
В граф додаються ребра ваги 0, які ведуть від
початку до всіх граничних вершин (i=1 | j=1) і з
граничних вершин (i=n | j=m) в кінець
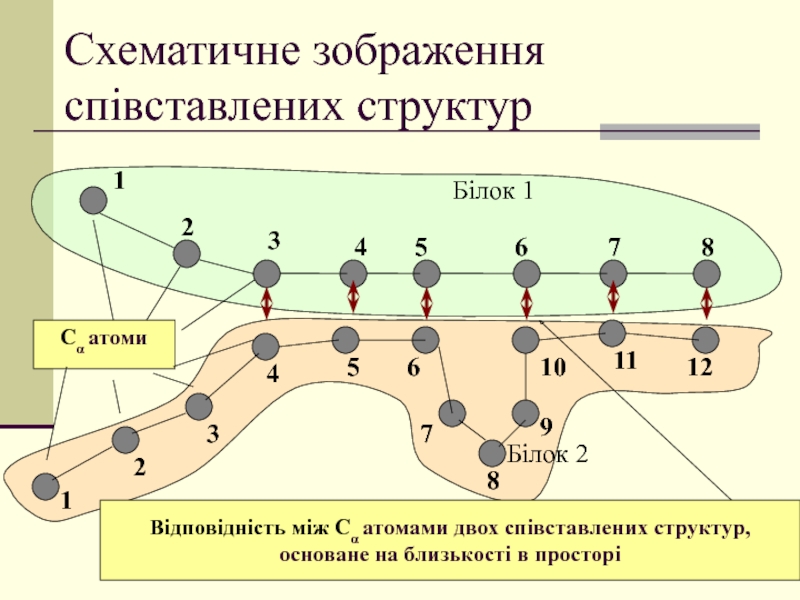
Слайд 43Схематичне зображення співставлених структур
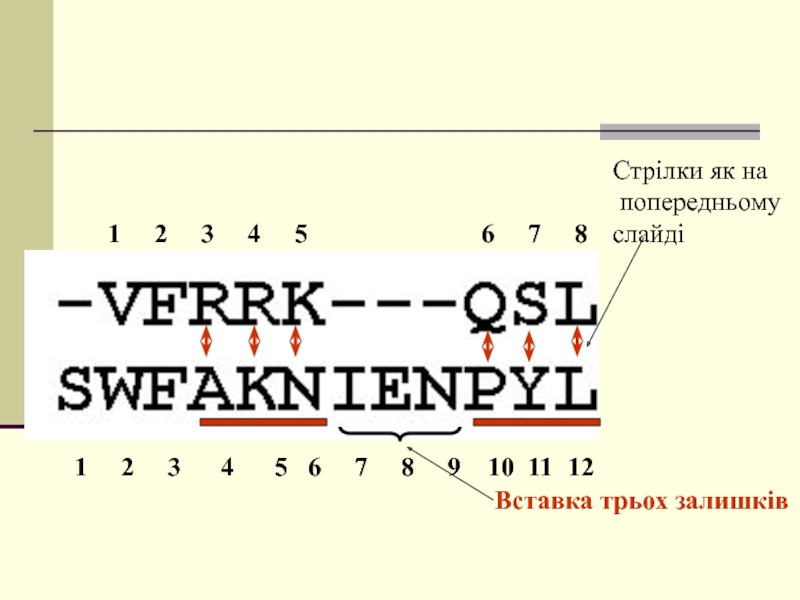
Слайд 44Стрілки як на
попередньому
слайді
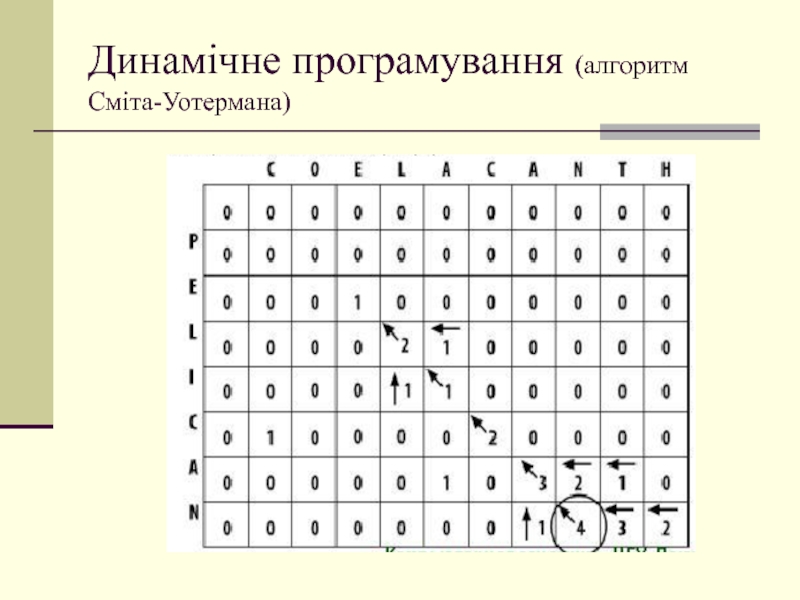
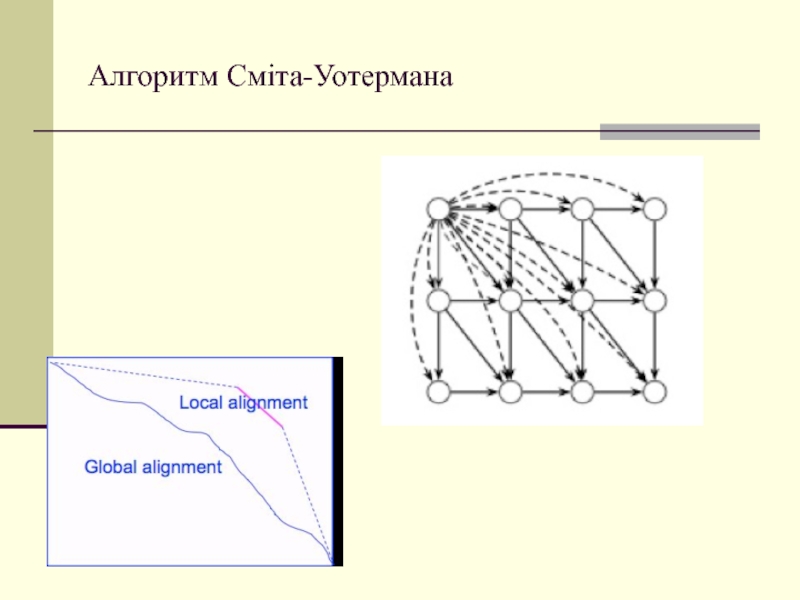
Слайд 45Динамічне програмування (алгоритм Сміта-Уотермана)
Слайд 48Значимість вирівнювань:
1.
Z-score=0 – схожість послідовностей випадкова;
Z-score≥5 – наявна
значимість вирівнювання.
2. P-value;
E-value.
Слайд 49Значимість вирівнювань:
P-value:
P≤10-100 – точне співпадіння;
P між 10-100 – 10-50 – послідовності майже ідентичні (наприклад, алелі чи поліморфізми);
P між 10-50 – 10-10 – близькоспоріднені послідовності (гомологія очевидна);
P між 10-5 – 10-1 – зазвичай далекоспоріднені послідовності;
P>10-1 – відповідність незначна.
Слайд 50Значимість вирівнювань: E-value
B-перетворюючий показних;
P-система підрахунку;
K-розмір області пошуку;
S-показник схожості послідовності.
m- довжина
досліджуваної послідовності;
n-довжина послідовності з бази даних.
Слайд 51Значимість вирівнювань:
Е-value:
Е≤0,02 – послідовності є гомологічними;
Е між 0,02 і 1
– гомологія не очевидна;
Е>1 – випадкове співпадіння.
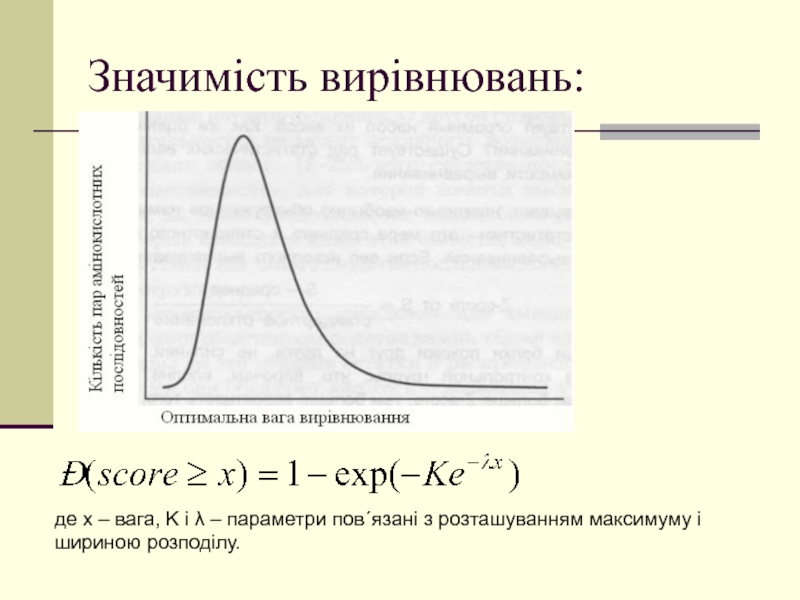
Слайд 52Значимість вирівнювань:
де х – вага, K і λ – параметри
пов´язані з розташуванням максимуму і шириною розподілу.
Слайд 53
Потребує параметр W (довжина слова).
Білки
W = 3
ДНК W = 11.
Алгоритм BLAST
(Basic Local
Alignment Search Tool)
Слайд 541. Пошук ідентичних\подібних ділянок
2. Спроба «видовжити» ці ділянки наскільки можливо
(тобто поки score росте)
В результаті: High-scoring Segment Pairs (HSPs)
THEFIRSTLINIHAVEADREAMESIRPATRICKREAD
INVIEIAMDEADMEATTNAMHEWASNINETEEN
Алгоритм BLAST (крок 1)
Слайд 55Спроба зєднати сусідні HSPs шляхом вирівнювання послідовностей між ними:
THEFIRSTLINIHAVEADREA____M_ESIRPATRICKREAD
INVIEIAMDEADMEATTNAMHEW___ASNINETEEN
Алгоритм BLAST (крок 2)
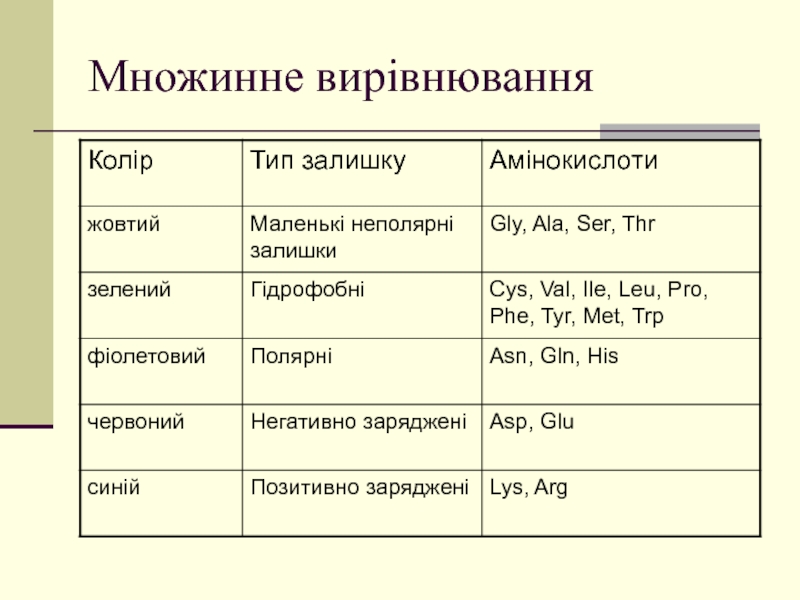
Слайд 56Методи для множинного вирівнювання:
Профілі;
Блоки;
Індикатори;
Закриті марківські моделі.
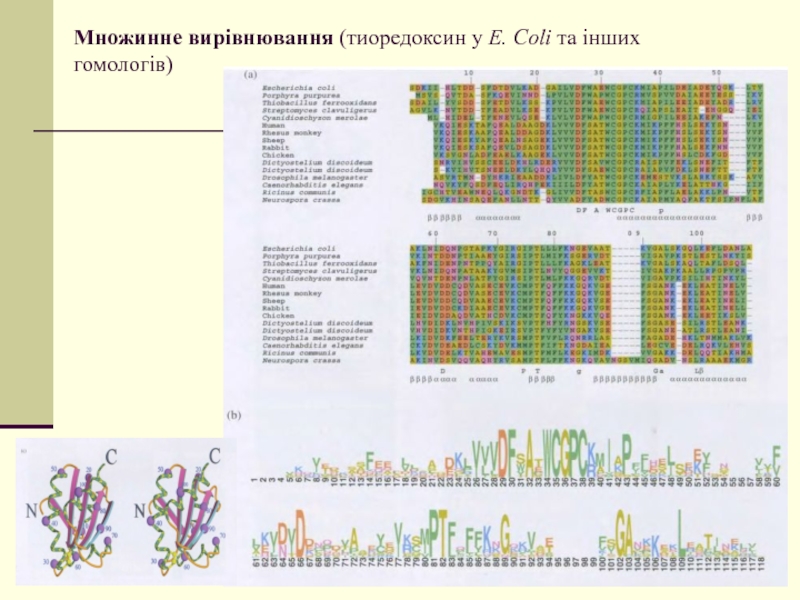
Слайд 58Множинне вирівнювання (тиоредоксин у E. Coli та інших гомологів)
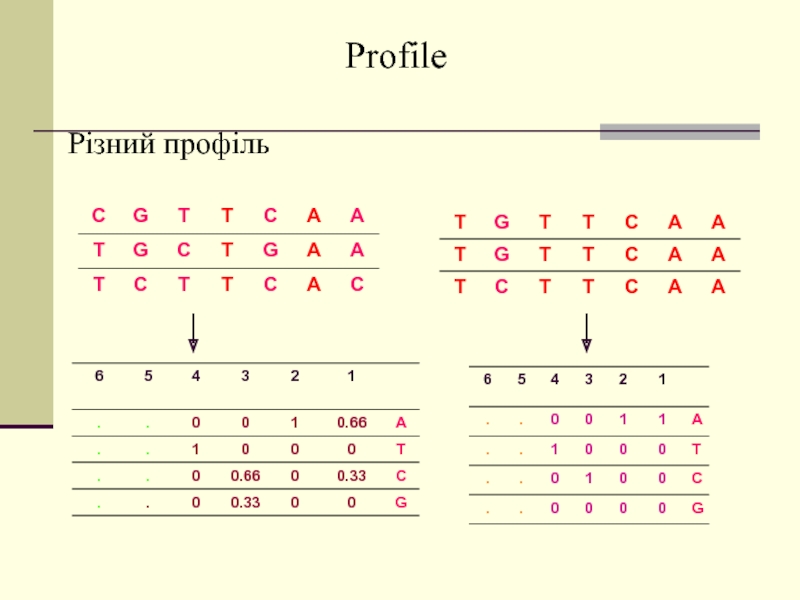
Слайд 59Профіль (Profile)
Профіль містить інформацію про символи в кожному стовпці вирівнювання.
Слайд 63Приховані марківські моделі
HMM (Hidden Markov Models)
Рис. 1. Структура Прихованої
марківської моделі. Кожній позиції у множинному вирівнюванні HMM відповідають стану
співставлення (m) і делеції (d). Стани вставки (і) з’являються між позиціями залишків, на початку і в кінці.
Слайд 64Дві дослідницькі групи, що спеціалізуються на біологічному застосуванні НММ, мають
Web-сервери і пропонують свої програми:
Слайд 65Алгоритми на основі компактності доменів:
САРОБ (Синтаксичний аналізатор розгорнутих одиниць білка)
– намагається максимізувати взаємодію в межах кожної структурної одиниці (домену)
і при цьому мінімізувати взаємодію між самими одиницями.
Домак – багатократно розділяє білок на дві довільні частини і обраховує “величину розщеплення” за кількістю контактів при кожному довільному розділенні.
Детектив – основана на допущенні про те, що кожний домен повинен містити гідрофобне ядро.
Слайд 66 Алгоритм “Струдл”
Використовує графову евристику Кернігана-Ліня
і розбиває білок на групи залишків, які показують мінімальну міжгрупову
взаємодію. Граф визначає зв'язки між вузлами і представлений матрицею. Починаючи з відповідного розбиття, “Струдл” мінімізує функцію вартості, яка залежить від взаємодій між вузлами. Для цього алгоритм виконує перестановку пар вузлів до тих пір, поки не буде отримано оптимального розбиття. Міжвузлові взаємодії визначаються за вирівняною діаграмою Вороного.
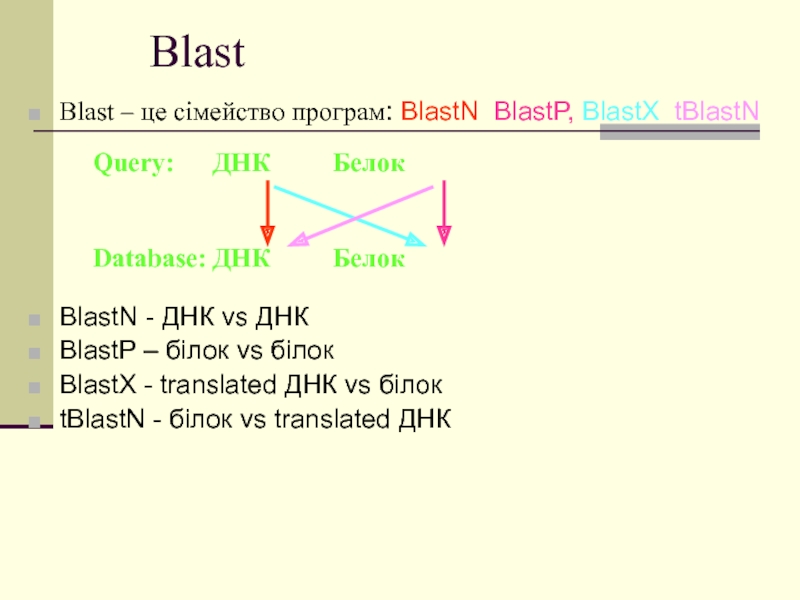
Слайд 73Blast
Blast – це сімейство програм: BlastN, BlastP, BlastX, tBlastN
BlastN -
ДНК vs ДНК
BlastP – білок vs білок
BlastX - translated ДНК
vs білок
tBlastN - білок vs translated ДНК
Query: ДНК Белок
Database: ДНК Белок