Тема Функции и структура программы Лекция 23.09.13г. 1

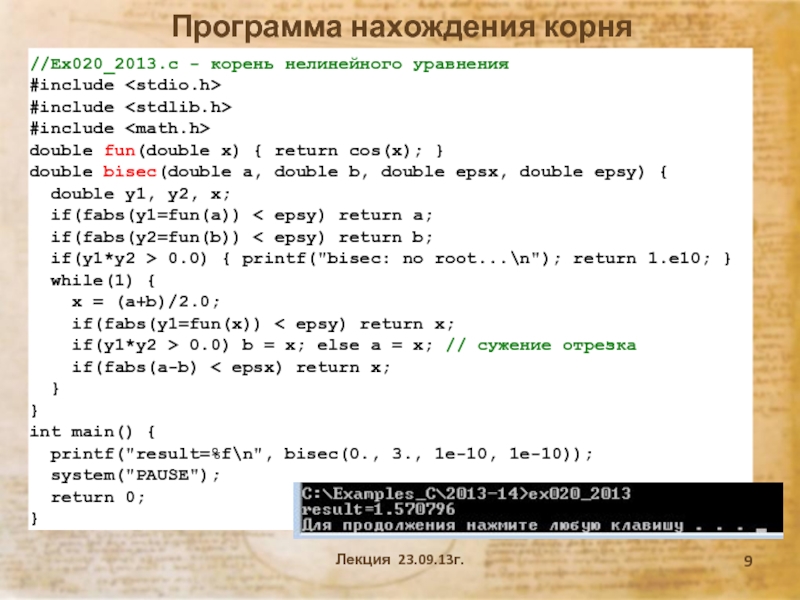
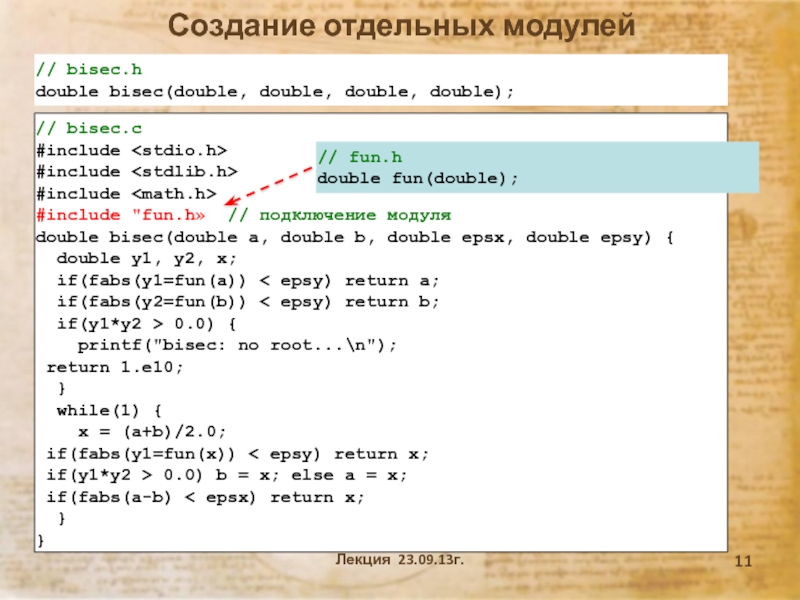
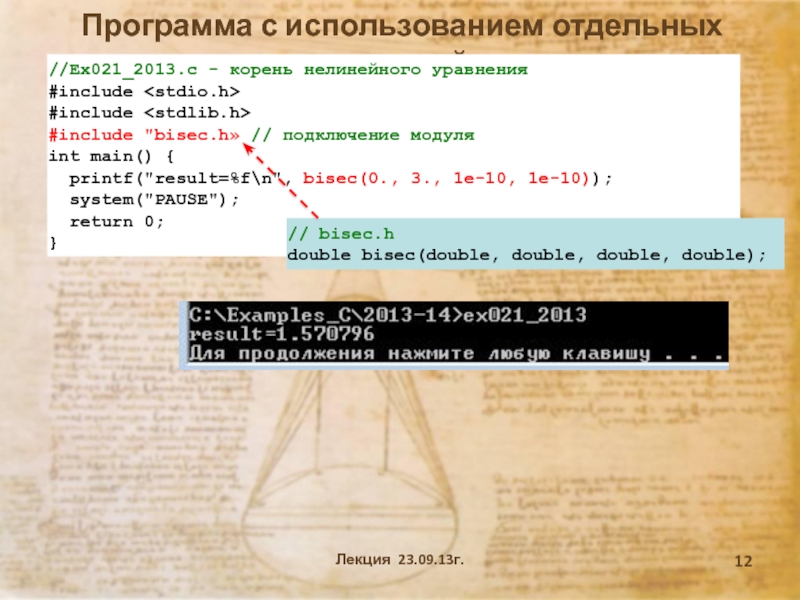
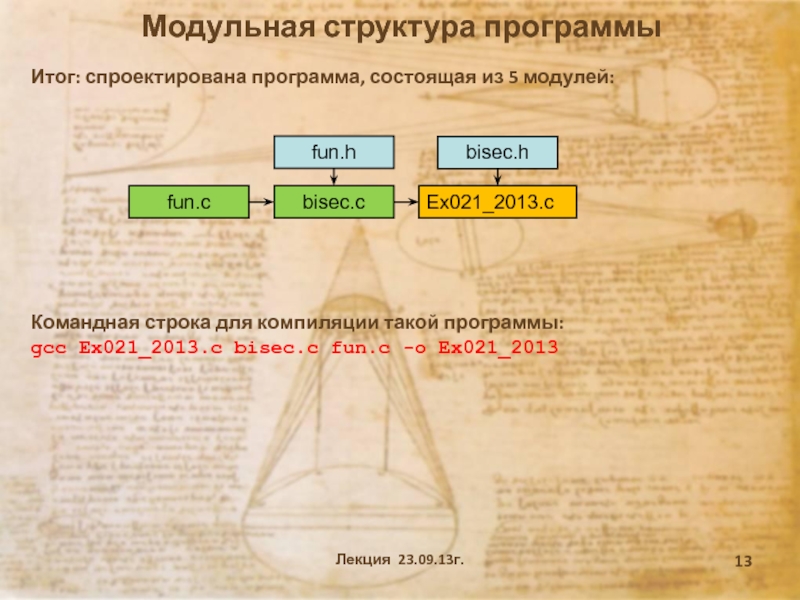
согласно которому программное средство (ПС) – программа, библиотека, web-приложение и

др. разделяется на отдельные сущности, называемые модулями. Модульность позволяет упростить задачи проектирования ПС и распределения процесса разработки ПС между группами разработчиков, а также позволяет реализовать методологию повторного использования кода.
При разбиении ПС на модули для каждого модуля указывается реализуемая им функциональность, а также связи с другими модулями. Роль модулей могут играть структуры данных, библиотеки функций, классы, сервисы и другие программные единицы, реализующие некоторую функциональность и предоставляющие интерфейс к ней.
В языке С модульность поддерживается функциями, препроцессоными командами, многофайловой структурой программы и заголовочными файлами.

более мелкие и позволяют инкапсулировать («упрятать» в оболочку) детали реализации

некоторой функциональности, предоставив пользователям («клиентам») формат обращения к этой функциональности (интерфейс). Это делает программу в целом более ясной и облегчает внесение в нее изменений.
Пример: функция, преобразующая символьное изображение числа, записанное в строке, в само число.

//atoi_.c
#include
int atoi_(char s[]) {
int i, n, sign;
for (i = 0; isspace(s[i]); i++) ;
sign = (s[i] == '-') ? -1 : 1;
if (s[i] == '+' || s[i] == '-')
i++;
for (n = 0; isdigit(s[i]); i++)
n = 10 * n + (s[i] - '0');
return sign * n;
}

//Ex025.c
#include
#include
int atoi_(char[]);
int main() {
int n = atoi_(" -347ab");
printf("n = %d\n", n);
system("PAUSE");
return 0;
}

интерфейс

реализация

т.е. описать её интерфейс (объяснить, как функцией можно воспользоваться) и

привести программный код, раскрывающий, как функция работает (записать реализацию функции на языке программирования).
Определение любой функции имеет следующую форму:
тип_возвращ_знач имя_функции(список_объявлений_арг) {
объявления и операторы
}
Различные части этого определения могут отсутствовать, но обязательными являются: имя_функции, пара круглых скобок и пара фигурных скобок, т.е. «минимальная» функция определяется так: fun(){} Это – «пустышка», которая не принимает никаких аргументов и ничего не делает (имеет пустое «тело»). Подобные функции могут использоваться в качестве «заглушек» при разработке программ.

Если при объявлении функции не указан тип возвращаемого значения, то по умолчанию подразумевается тип int.

и
функций.
Функции обмениваются данными посредством передачи аргументов и возвращения

значений, а также через внешние переменные.
Функции могут следовать друг за другом в файле исходного кода в любом порядке, и текст программы можно разбивать на любое количество файлов, но при этом запрещается разбивать текст функции между файлами.
Функция не может быть определена внутри другой функции
В результате своей работы функция может возвратить в вызывающую ее функцию результат – некоторое значение, тип которого объявлен перед именем функции. Для этого в теле функции должен присутствовать хотя бы один оператор возврата вида: return выражение; Вызывающая функция может игнорировать (т.е. не использовать) возвращаемое значение.
Существует еще одна форма оператора возврата: return; В этом случае в вызывающую функцию ничего не передается, а при определении функции в качестве типа возвращаемого значения указывается void.
Тело функции может не содержать оператора возврата return ; при этом возврат из функции происходит при достижении конца блока (закрывающей скобки } ).

значению, т.е. функция получает значения своих аргументов в виде временных

переменных, а не оригиналов. Следовательно, все действия функции со своими аргументами никак не отражаются на переменных, переданных функции при вызове. Исправить это положение можно с помощью указателей.
Пример: функция, производящая «обмен значениями» двух переменных.

//Ex026_err.c – Err!!!
#include
#include
void swap(int a, int b) {
int c = a;
a = b; b = c;
}
int main() {
int x = 5, y = 7;
printf("x = %d, y = %d\n",x,y);
swap(x, y);
printf("x = %d, y = %d\n",x,y);
system("PAUSE");
return 0;
}

//Ex026_ok.c – Ok!!!
#include
#include
void swap(int *a, int *b) {
int c = *a;
*a = *b; *b = c;
}
int main() {
int x = 5, y = 7;
printf("x = %d, y = %d\n",x,y);
swap(&x, &y);
printf("x = %d, y = %d\n",x,y);
system("PAUSE");
return 0;
}

условии: в программе обязательно должна присутствовать в точности одна функция

с именем main («главная» функция), т.к. запуск программы на выполнение операционной системой производится всегда через эту функцию (т.е. main начинает выполняться первой).
Функция main всегда имеет тип возвращаемого значения int, через это значение ОС уведомляется об успешности или не успешности завершения программы (т.н. «код завершения»). А т.к. int подразумевается «по умолчанию», то тип возвращаемого значения для main часто не указывают.
Существует две формы main:
без аргументов – main() и
с аргументами – main(int argc, char *argv[])
Вторая форма main позволяет при вызове программы из командной строки передать в нее произвольное количество строковых аргументов (об этом позже).

уравнения f(x)=0 методом деления отрезка пополам:
Даны: отрезок [a, b], на

котором предположительно находится корень; точность определения нуля функции – epsy и точность определения корня – epsx.

double fun(double x) { return cos(x); }
double bisec(double a, double

b, double epsx, double epsy) {
double y1, y2, x;
if(fabs(y1=fun(a)) < epsy) return a;
if(fabs(y2=fun(b)) < epsy) return b;
if(y1*y2 > 0.0) { printf("bisec: no root...\n"); return 1.e10; }
while(1) {
x = (a+b)/2.0;
if(fabs(y1=fun(x)) < epsy) return x;
if(y1*y2 > 0.0) b = x; else a = x; // сужение отрезка
if(fabs(a-b) < epsx) return x;
}
}
int main() {
printf("result=%f\n", bisec(0., 3., 1e-10, 1e-10));
system("PAUSE");
return 0;
}

bisec() в отдельных файлах и создадим для них заголовочные (интерфейсные)

файлы:

// fun.c
#include
double fun(double x) {
return cos(x);
}

// fun.h
double fun(double);

подключение модуля
double bisec(double a, double b, double epsx, double epsy)

{
double y1, y2, x;
if(fabs(y1=fun(a)) < epsy) return a;
if(fabs(y2=fun(b)) < epsy) return b;
if(y1*y2 > 0.0) {
printf("bisec: no root...\n");
return 1.e10;
}
while(1) {
x = (a+b)/2.0;
if(fabs(y1=fun(x)) < epsy) return x;
if(y1*y2 > 0.0) b = x; else a = x;
if(fabs(a-b) < epsx) return x;
}
}

// bisec.h
double bisec(double, double, double, double);

// fun.h
double fun(double);

#include
#include "bisec.h» // подключение модуля
int main() {
printf("result=%f\n", bisec(0.,

3., 1e-10, 1e-10));
system("PAUSE");
return 0;
}

// bisec.h
double bisec(double, double, double, double);

строка для компиляции такой программы:
gcc Ex021_2013.c bisec.c fun.c -o Ex021_2013
fun.h

отражения, производимые двумя точно параллельными друг другу зеркалами, являются одной

из форм бесконечной рекурсии.
Наиболее общее применение рекурсия находит в математике и информатике. Здесь она является методом определения функций, при котором определяемая функция применена в теле своего же собственного определения. При этом бесконечный набор случаев (значений функции) описывается с помощью конечного выражения, которое для некоторых случаев может ссылаться на другие случаи, если при этом не возникает циклов или бесконечной цепи ссылок. Фактически это способ определения множества объектов через самого себя с использованием ранее заданных частных определений.

так :
n! = n * (n-1)! , 0! = 1.
Числа

Фибоначчи: Fn = Fn-1 + Fn-2, F1 = F2 = 1.
Практически все геометрические фракталы задаются в форме бесконечной рекурсии, например, треугольник Серпинского:

неё же самой, непосредственно (простая рекурсия) или через другие функции

(сложная или косвенная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы возможно описать бесконечное вычисление, причём без явных повторений частей программы.

// генератор чисел Фибоначчи
#include
#include
int fib(int i) {
if (i < 3) return 1;
return fib(i-1)+fib(i-2);
}
int main() {
int i;
for (i=1; i<11; i++) printf("F(%d) = %d\n", i, fib(i));
system("PAUSE");
return 0;
}

числа:
// рекурсия (факториал)
#include
#include
int fact(int n) {
return (n>2)

? n * fact(n-1) : n;
}
main() {
int n;
for(n = 0; n < 10; n++)
printf("%2d! = %10d\n", n, fact(n));
system("PAUSE");
return 0;
}

под названием Ханойской башни. Игра начинается, когда n дисков разного

диаметра расположены по возрастанию диаметров на одном из трех стержней. Цель игры — по одному перенести диски, чтобы они в конечном счете были расположены в том же порядке на другом стержне. Не разрешается класть диск большего диаметра на диск меньшего диаметра. Разработать алгоритм, который проделывает эту процедуру за 2n-1 операций, где под операцией подразумевается перемещение диска с одного стержня на другой.

A

B

C

1

2

3

4

A

B

C

5

6

7

8

A

B

C

9

10

11

12

A

B

C

13

14

15

C

задачу.
#include
#include
int k;
void mov(int n, char a, char c,

char b) {
if (n < 1) return;
mov(n-1, a, b, c);
printf("%2d: %c -> %c\n", ++k, a, c);
mov(n-1, b, c, a);
}
int main() {
int m;
while (1) {
printf("Input m: "); scanf("%d", &m);
if (m == 0) break;
k = 0;
mov(m, 'A', 'C', 'B');
printf("------------\n");
}
system("PAUSE");
return 0;
}

количество единиц в двоичном представлении заданного числа n. Если да

– то программа выдает 1, в противном случае – 0.

true};
int g0 (int);
int g1 (int);
int main() {
int n;
while(1)

{
printf("enter the number (>0): "); scanf("%d", &n);
if( n == 0) break;
printf("result=%d\n", g0(n));
}
system("PAUSE");
return 0;
}
int g0 (int n) {
if( n == 0) return true;
if( n & 01 == 0) return g0(n >> 1);
return g1(n >> 1); }
int g1 (int n) {
if( n == 0) return false;
if( n & 01 == 0) return g1(n >> 1);
return g0(n >> 1); }