Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРИЯ ЭКОНОМИЧЕСКОГО АНАЛИЗА
Содержание
- 1. ТЕОРИЯ ЭКОНОМИЧЕСКОГО АНАЛИЗА
- 2. Экономический анализ НаукаСистема специальных знанийОснова - законы
- 3. Предмет и объект экономического анализаПредметом экономического анализа
- 4. Принципы экономического анализа:научность;системность;комплексность;объективность и конкретность;действенность;оперативность;массовость;государственный подход;эффективность.
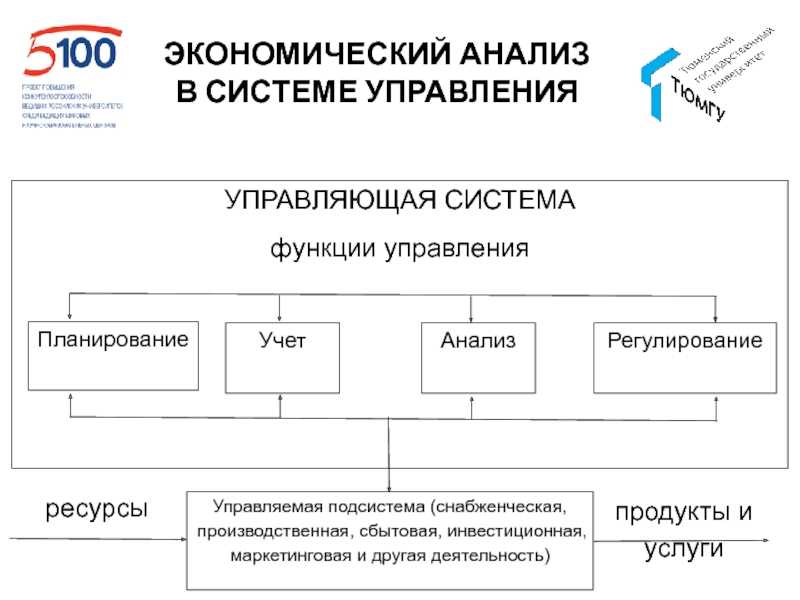
- 5. ЭКОНОМИЧЕСКИЙ АНАЛИЗ В СИСТЕМЕ УПРАВЛЕНИЯ
- 6. Метод экономического анализа
- 7. Методика экономического анализаМетодика экономического анализа - совокупность
- 8. КЛАССИФИКАЦИЯ АНАЛИТИЧЕСКИХ ПОКАЗАТЕЛЕЙ
- 9. По содержанию:количественные; качественные.
- 10. По содержанию:количественные; Чр, МЗ, ОПФсркачественные.
- 11. По содержанию:количественные; Чр, МЗ, ОПФсркачественные.Вг = ТП/ЧрМО(материалоотдача)= ТП/МЗФО=ТП/ОПФср
- 12. По способу выражения:абсолютные;относительные.
- 13. По способу выражения:абсолютные;относительные.
- 14. Абсолютные показателиВ зависимости от применяемых измерителей абсолютные показатели могут быть:натуральными;стоимостными;трудовыми.
- 15. Абсолютные показателиВ зависимости от порядка исчисления абсолютные показатели могут быть: интервальными;моментными;среднехронологическими.
- 16. Относительные показателиВ зависимости от характера используемых в расчетах абсолютных показателей различают следующие относительные показатели:коэффициенты; удельные; структурные.
- 17. Относительные показателиВ зависимости от характера используемых в
- 18. Относительные показателиВ зависимости от характера используемых в
- 19. Относительные показателиВ зависимости от характера используемых в
- 20. По широте использования: общие;специфические.
- 21. По характеру использования:показатели-характеристики;показатели-факторы.ТП = Чр * Вг
- 22. СРАВНЕНИЕ КАК ЭЛЕМЕНТ МЕТОДИКИ АНАЛИЗА
- 23. СРАВНЕНИЕСущность сравнения – сопоставление однородных объектов с целью выявления сходства либо различий между ними.
- 24. ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗАгоризонтальный сравнительный анализ;вертикальный сравнительный анализ;трендовый анализ;динамические (временные) сравнения;статические (пространственные) сравнения;одномерный сравнительный анализ;многомерный сравнительный анализ.
- 25. ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗАгоризонтальный сравнительный анализ – применяется
- 26. ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗАвертикальный сравнительный анализ – предполагает
- 27. ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗАтрендовый анализ – используется при
- 28. ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗАдинамические (временные) сравнения – применяются для изучения изменения явлений во времени.
- 29. ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗАстатические (пространственные) сравнения – используются
- 30. ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗАодномерный сравнительный анализ – проводится
- 31. ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗАмногомерный сравнительный анализ – сопоставляются результаты деятельности нескольких предприятий по широкому спектру показателей.
- 32. МНОГОМЕРНЫЙ СРАВНИТЕЛЬНЫЙ АНАЛИЗЭтап 1.Обосновывается система показателей, по
- 33. МНОГОМЕРНЫЙ СРАВНИТЕЛЬНЫЙ АНАЛИЗЭтап 2.Определяется максимальный элемент, который
- 34. МНОГОМЕРНЫЙ СРАВНИТЕЛЬНЫЙ АНАЛИЗЭтап 3. Все элементы матрицы
- 35. МНОГОМЕРНЫЙ СРАВНИТЕЛЬНЫЙ АНАЛИЗЭтап 4.Полученные значения рейтинговой оценки (Rj) ранжируются и определяется рейтинг каждого предприятия.
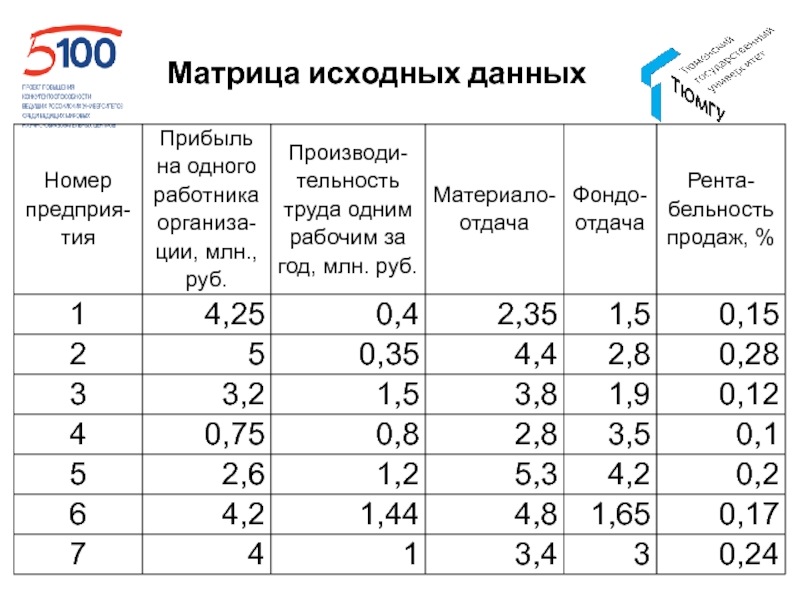
- 36. Матрица исходных данных
- 37. Группировка и детализация как элементы методики анализа
- 38. Детализация – аналитический прием расчленения общих показателей на составные части.
- 39. Детализация по времени
- 40. Детализация по времени позволяет проследить за равномерностью совершения хозяйственных процессов.
- 41. Детализация по месту
- 42. Детализация по месту означает разделение общих по предприятию показателей в разрезе цехов, участков, бригад.
- 43. Детализация показателей по составным частям
- 44. Детализация показателей по составным частям необходима для
- 45. Группировка – деление массы изучаемой совокупности объектов на количественно однородные группы по соответствующим признакам.
- 46. Типологические группировки
- 47. Типологические группировки предназначены для расчленения всей совокупности первичных данных на однокачественные группы и классы.
- 48. Структурные группировки.
- 49. Структурные группировки применяются при изучении состава предприятий и структуры выпускаемой продукции.
- 50. Аналитические группировки
- 51. Аналитические группировки предназначены для выявления взаимосвязи между анализируемыми экономическими явлениями.
- 52. ВЗАИМОСВЯЗЬ ЭЛЕМЕНТОВ ХОЗЯЙСТВЕННОГО ПРОЦЕССА
- 53. Виды взаимосвязейдетерминированные (функциональные);вероятностные (стохастические).
- 54. Виды взаимосвязейдетерминированные (функциональные)Функциональные связи характеризуются строгим соответствием
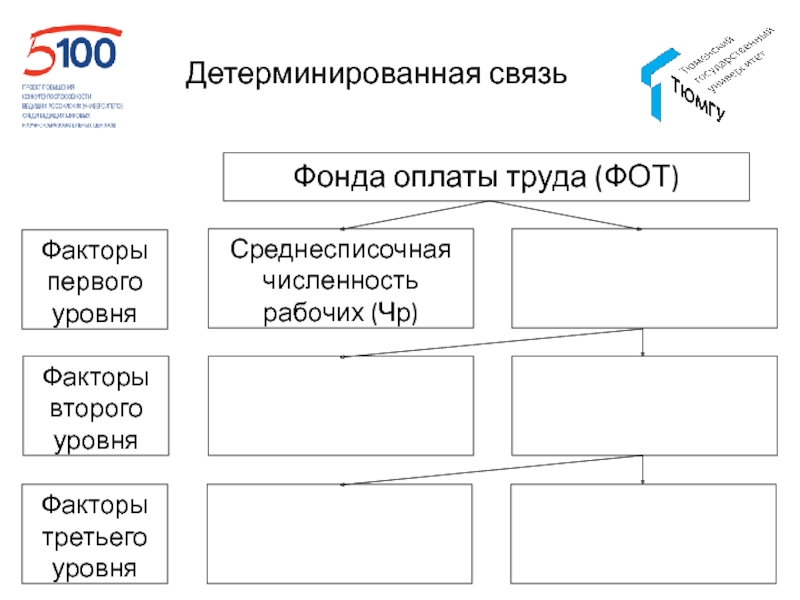
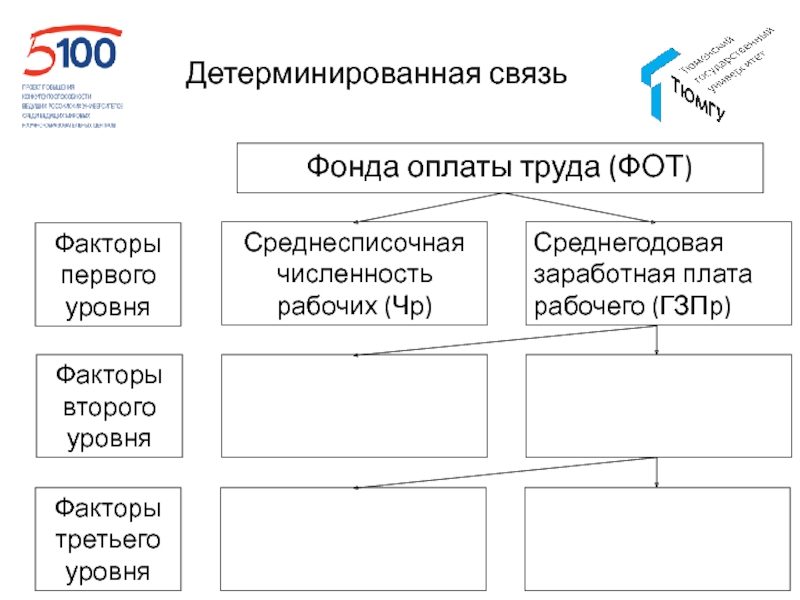
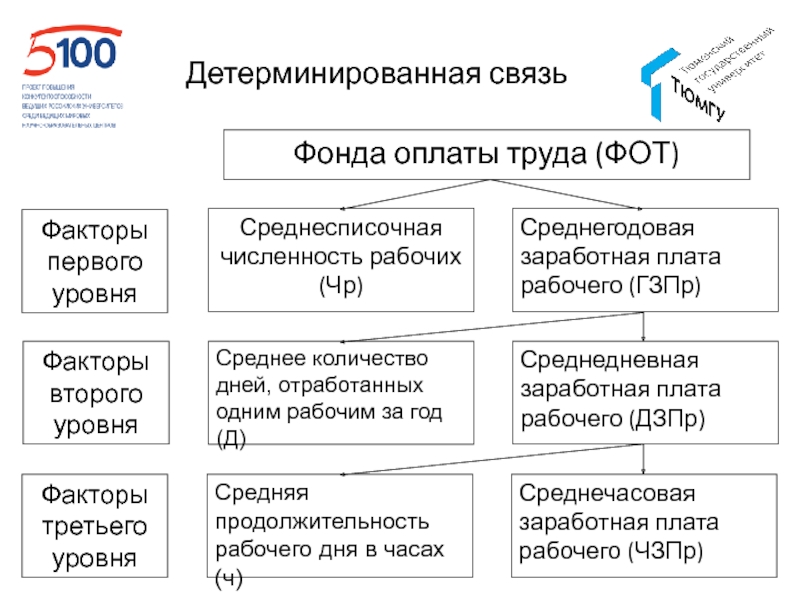
- 55. Детерминированная связь
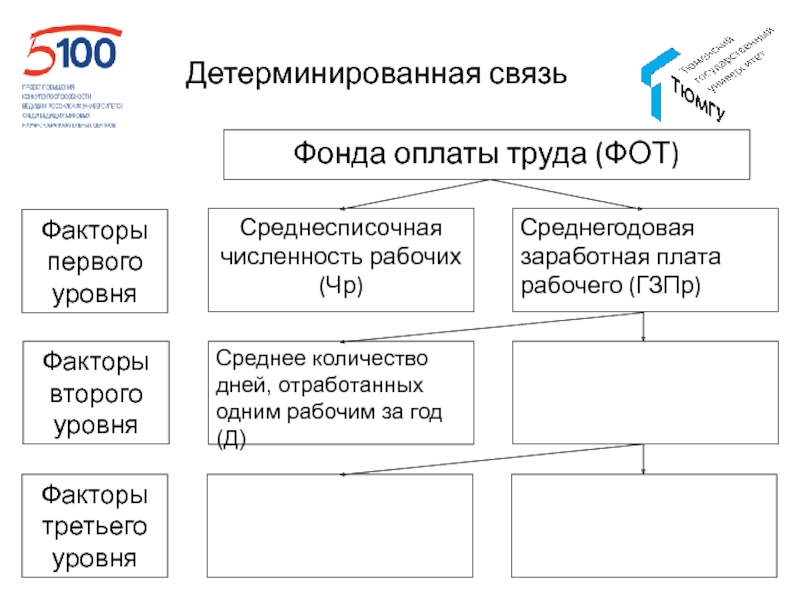
- 56. Детерминированная связь
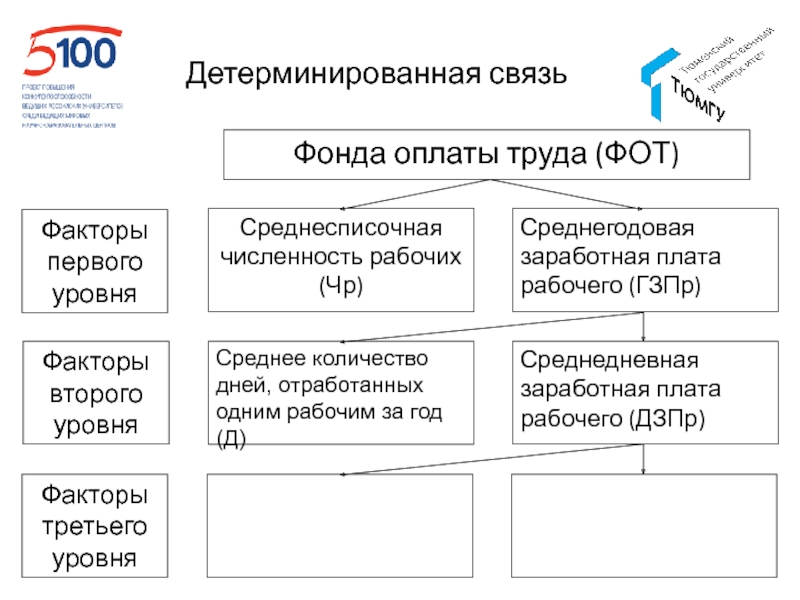
- 57. Детерминированная связь
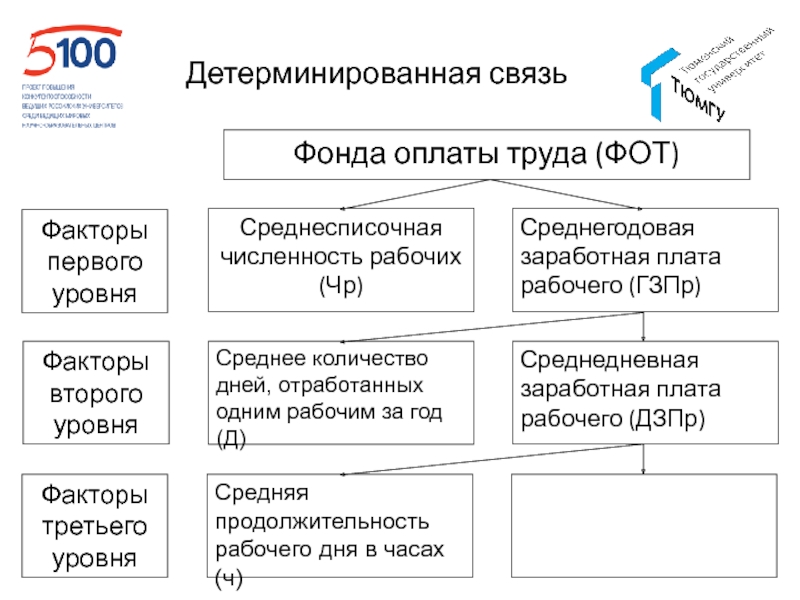
- 58. Детерминированная связь
- 59. Детерминированная связь
- 60. Детерминированная связь
- 61. Виды взаимосвязейвероятностные (стохастические)При вероятностных связях между причиной
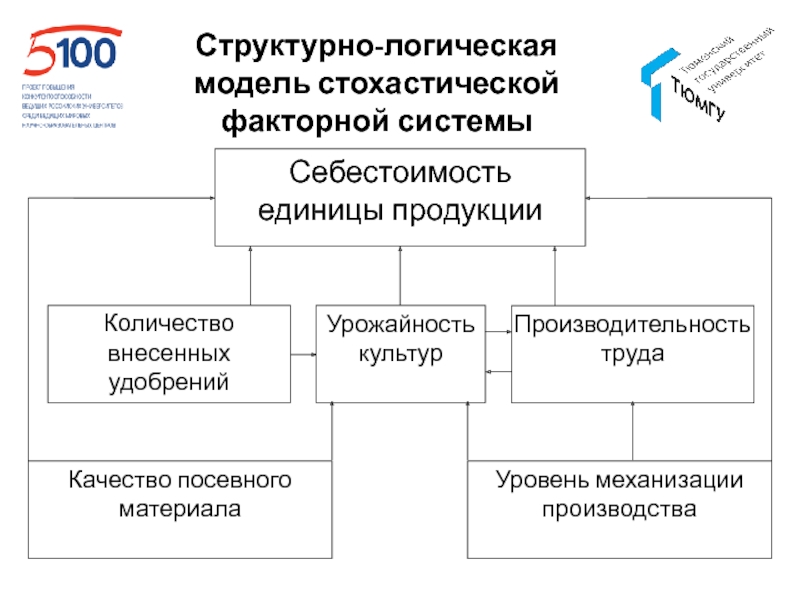
- 62. Структурно-логическая модель стохастической факторной системы
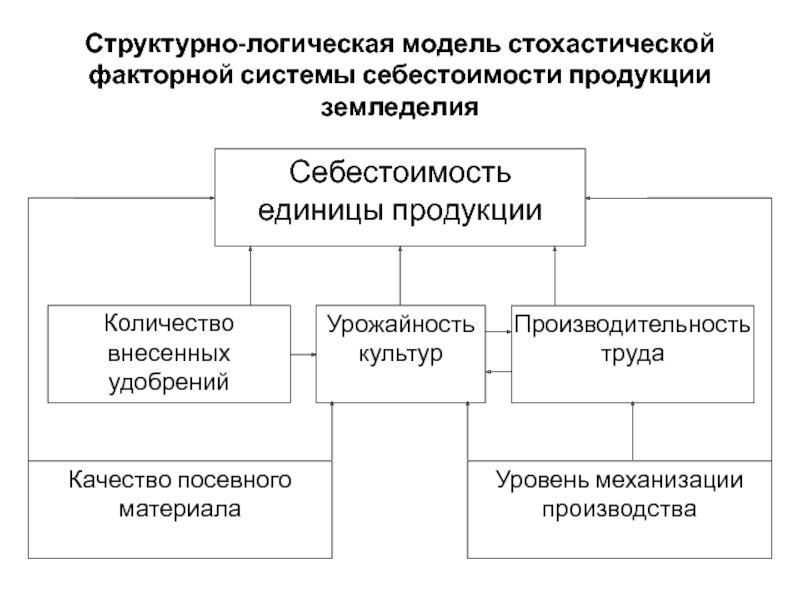
- 63. Структурно-логическая модель стохастической факторной системы себестоимости продукции земледелия
- 64. Виды функциональных зависимостей- аддитивные;мультипликативные;кратные- комбинированные.
- 65. Аддитивная функциональная зависимость РП = ВП +
- 66. Мультипликативная функциональная зависимость ТП= Чр • Д
- 67. Кратная функциональная зависимость
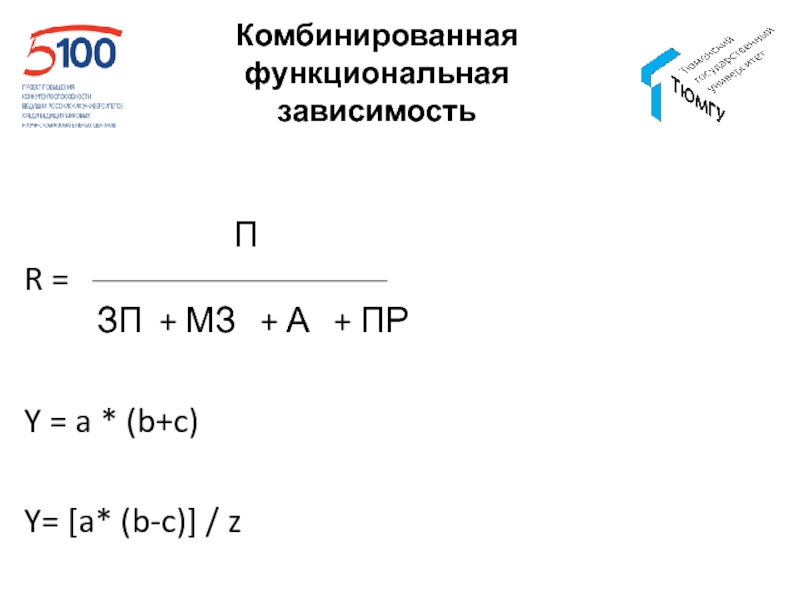
- 68. Комбинированная функциональная зависимость
- 69. Элиминирование как элемент методики анализа
- 70. Элиминирование представляет
- 71. ЭлиминированиеСпособы элиминирования:- цепных подстановок;- абсолютных отклонений;способ процентных разниц;индексный;интегральный.
- 72. Схема анализа способом цепных подстановокТП= Чр • Вг кол. кач.n, то подстановок n-1
- 73. Схема анализа способом цепных подстановокТП= Чр • ВгТП0 = Чр0 • Вг0;
- 74. Схема анализа способом цепных подстановокТП= Чр • ВгТП0 = Чр0 • Вг0; I подстановкаТП I =
- 75. Схема анализа способом цепных подстановокТП= Чр •
- 76. Схема анализа способом цепных подстановокТП= Чр •
- 77. Схема анализа способом цепных подстановокТП= Чр •
- 78. Схема анализа способом цепных подстановокТП= Чр •
- 79. Схема анализа способом цепных подстановокТП= Чр •
- 80. Схема анализа способом цепных подстановокТП= Чр •
- 81. Схема анализа способом цепных подстановокТП= Чр •
- 82. Схема анализа способом цепных подстановокТП= Чр •
- 83. Схема анализа способом цепных подстановокТП= Чр •
- 84. Схема анализа способом цепных подстановокТП= Чр •
- 85. Схема анализа способом цепных подстановокТП= Чр •
- 86. Схема анализа способом цепных подстановок ТП= Чр
- 87. Схема анализа способом цепных подстановок ТП= Чр
- 88. Схема анализа способом цепных подстановок
- 89. Схема анализа способом цепных подстановок
- 90. Схема анализа способом цепных подстановок
- 91. Схема анализа способом цепных подстановок
- 92. Схема анализа способом цепных подстановок
- 93. Схема анализа способом цепных подстановок
- 94. Схема анализа способом цепных подстановок
- 95. Схема анализа способом цепных подстановок
- 96. Схема анализа способом цепных подстановок
- 97. Схема анализа способом цепных подстановок
- 98. Схема анализа способом цепных подстановок
- 99. Схема анализа способом цепных подстановок
- 100. Схема анализа способом цепных подстановок
- 101. Схема анализа способом цепных подстановок
- 102. Схема анализа способом цепных подстановок
- 103. Схема анализа способом цепных подстановок
- 104. проверка∆ТП = ТП1 - ТП0 == ∆ТП(Чр) + ∆ТП(Д) + ∆ТП(ч) + ∆ТП(Вч)
- 105. Схема анализа способом абсолютных отклоненийТП= Чр • Д • ч • Вч
- 106. Схема анализа способом абсолютных отклоненийТП= Чр • Д • ч • Вч∆ТП(Чр)=
- 107. Схема анализа абсолютных отклоненийТП= Чр • Д • ч • Вч∆ТП(Чр)= (Чр1 – Чр0)
- 108. Схема анализа способом абсолютных отклоненийТП= Чр •
- 109. Схема анализа способом абсолютных отклоненийТП= Чр •
- 110. Схема анализа способом абсолютных отклоненийТП= Чр •
- 111. Схема анализа способом абсолютных отклоненийТП= Чр •
- 112. Схема анализа способом абсолютных отклоненийТП= Чр •
- 113. Схема анализа способом абсолютных отклоненийТП= Чр •
- 114. Схема анализа способом абсолютных отклоненийТП= Чр •
- 115. Схема анализа способом абсолютных отклоненийТП= Чр •
- 116. Схема анализа способом абсолютных отклоненийТП= Чр •
- 117. Схема анализа способом абсолютных отклоненийТП= Чр •
- 118. Схема анализа способом абсолютных отклоненийТП= Чр •
- 119. Схема анализа способом абсолютных отклоненийТП= Чр •
- 120. Схема анализа способом абсолютных отклоненийТП= Чр •
- 121. Схема анализа способом абсолютных отклоненийТП= Чр •
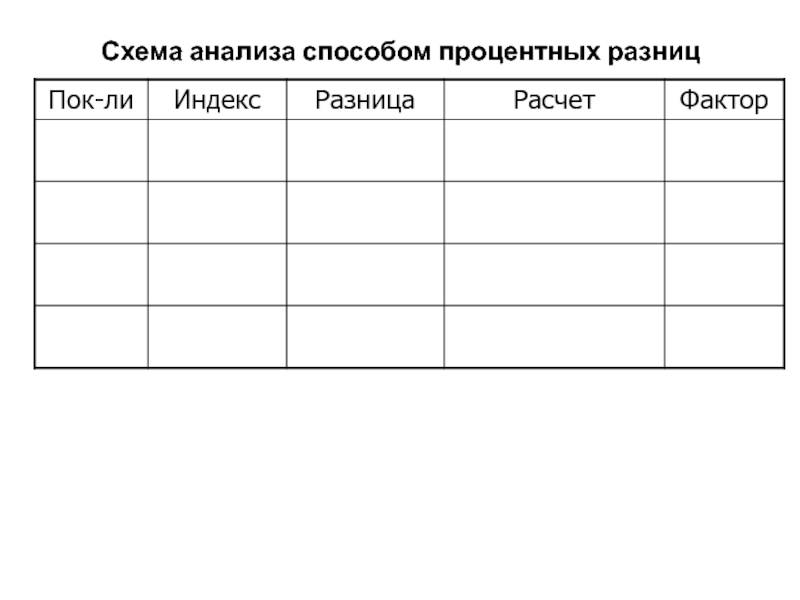
- 122. Схема анализа способом процентных разницТП= Чр • Д • ч • Вч
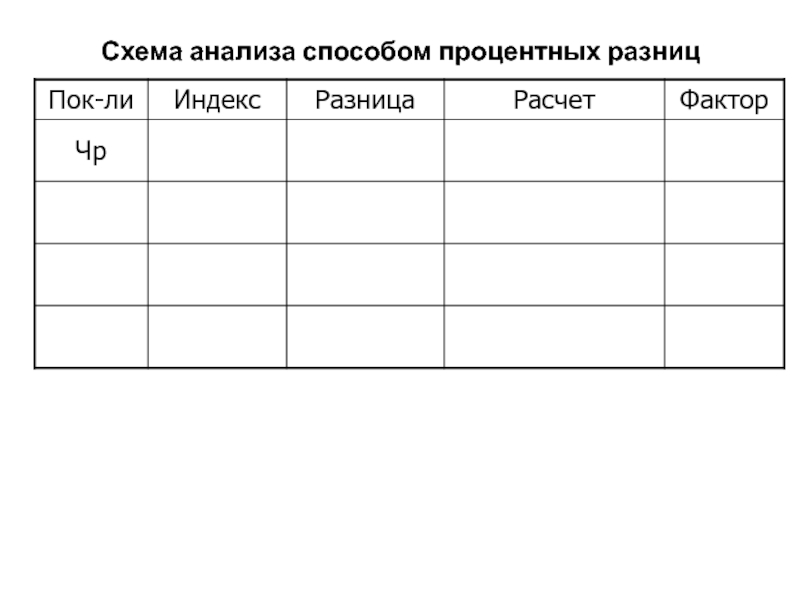
- 123. Схема анализа способом процентных разниц
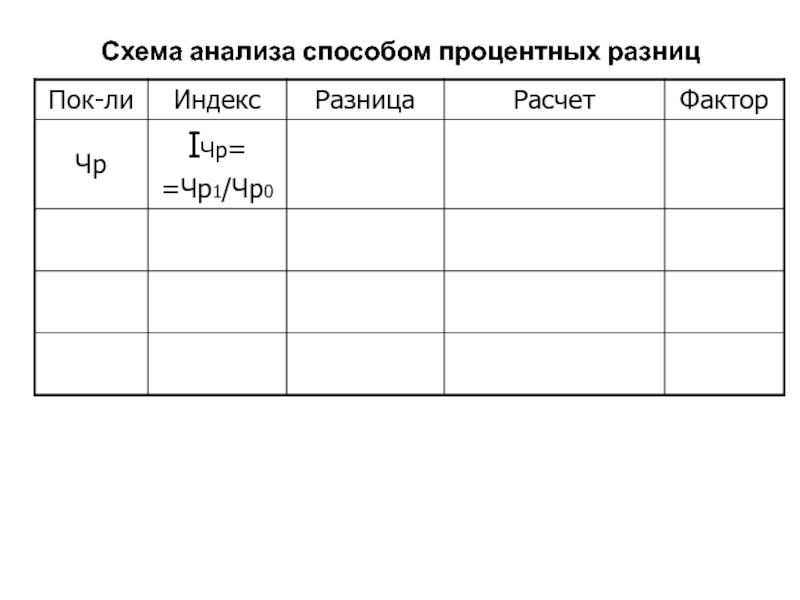
- 124. Схема анализа способом процентных разниц
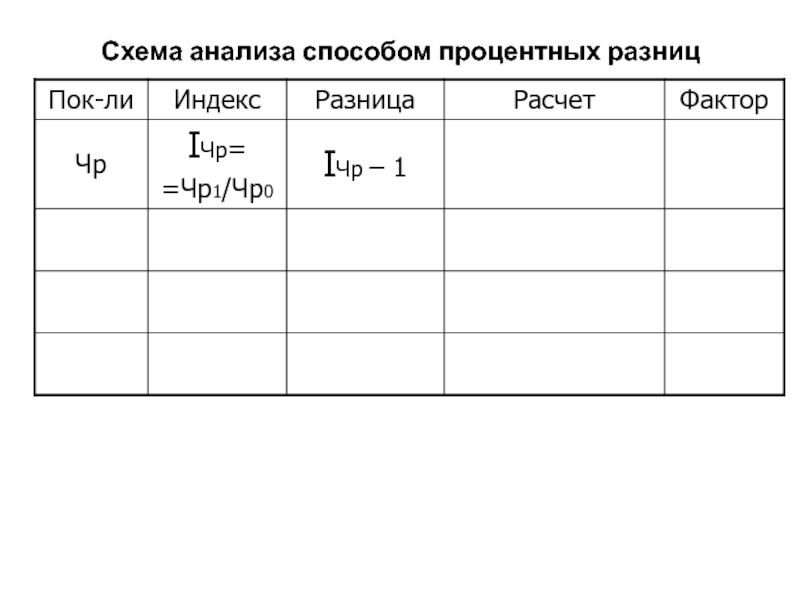
- 125. Схема анализа способом процентных разниц
- 126. Схема анализа способом процентных разниц
- 127. Схема анализа способом процентных разниц
- 128. Схема анализа способом процентных разниц
- 129. Схема анализа способом процентных разниц
- 130. Схема анализа способом процентных разниц
- 131. Схема анализа способом процентных разниц
- 132. Схема анализа способом процентных разниц
- 133. Схема анализа способом процентных разниц
- 134. Схема анализа способом процентных разниц
- 135. Схема анализа способом процентных разниц
- 136. Схема анализа способом процентных разниц
- 137. Схема анализа способом процентных разниц
- 138. Схема анализа способом процентных разниц
- 139. Схема анализа способом процентных разниц
- 140. Схема анализа способом процентных разниц
- 141. Схема анализа способом процентных разниц
- 142. Схема анализа способом процентных разниц
- 143. проверка∆ТП = ТП1 - ТП0 == ∆ТП(Чр) + ∆ТП(Д) + ∆ТП(ч) + ∆ТП(Вч)
- 144. Схема анализа индексным способомТП= Чр • Д • ч • Вч
- 145. Схема анализа индексным способомТП= Чр • Д
- 146. Схема анализа индексным способомТП= Чр • Д • ч • ВчIЧр= Чр1•Д0•ч0•Вч0/Чр0•Д0•ч0•Вч0;
- 147. Схема анализа индексным способомТП= Чр • Д
- 148. Схема анализа индексным способомТП= Чр • Д • ч • ВчIЧр= Чр1•Д0•ч0•Вч0/Чр0•Д0•ч0•Вч0;IД= Чр1•Д1•ч0•Вч0/Чр1•Д0•ч0•Вч0;Iч= Чр1•Д1•ч1•Вч0/Чр1•Д1•ч0•Вч0;
- 149. Схема анализа индексным способомТП= Чр • Д • ч • ВчIЧр= Чр1•Д0•ч0•Вч0/Чр0•Д0•ч0•Вч0;IД= Чр1•Д1•ч0•Вч0/Чр1•Д0•ч0•Вч0;Iч= Чр1•Д1•ч1•Вч0/Чр1•Д1•ч0•Вч0;IВч= Чр1•Д1•ч1•Вч1/Чр1•Д1•ч1•Вч0;
- 150. Схема анализа индексным способомТП= Чр • Д
- 151. Схема анализа индексным способомТП= Чр • Д
- 152. Схема анализа интегральным способомТП= Чр • Вг
- 153. Схема анализа интегральным способомТП= Чр • Вг∆ТП(Чр)= ∆Чр • Вг0 +
- 154. Схема анализа интегральным способомТП= Чр • Вг∆ТП(Чр)= ∆Чр • Вг0 + 0,5 • ∆Чр • ∆Вг;
- 155. Схема анализа интегральным способомТП= Чр • Вг∆ТП(Чр)=
- 156. Схема анализа интегральным способомТП= Чр • Вг∆ТП(Чр)=
- 157. Схема анализа интегральным способомТП= Чр • Вг∆ТП(Чр)=
- 158. ПРИМЕРУстановить влияние на товарооборот изменения торговой площади
- 159. ПРИМЕРТО1м.кв. =ТО / ТпТО = Тп *
- 160. ПРИМЕРУстановить влияние на объем товарной продукции изменения
- 161. ПРИМЕРФО =ТП / ОПФ
- 162. ПРИМЕР∆ТП= ТП 1 – ТП 0 = ∆ОПФ=∆ФО=
- 163. ПРИМЕРIТП= ТП1 / ТП0IОПФ=IФО=
- 164. ПРИМЕРФО =
- 165. ПРИМЕРТП0= ОПФ0 * ФО0 =50000 * 2,5
- 166. ПРИМЕР∆ТП(ОПФ)= (ОПФ1 – ОПФ0) * ФО0 =
- 167. ПРИМЕР∆ТП(ОПФ)= (ОПФ1 – ОПФ0) * ФО0 =
- 168. ПРИМЕРТП = ОПФ * ФО∆ТП(ОПФ)= (IОПФ –
- 169. ПРИМЕРТП = ОПФ * ФОIОПФ = (
- 170. ПРИМЕРТП = ОПФ * ФО∆ТП(ОПФ)=∆ОПФ * ФО0
- 171. КЛАССИФИКАЦИЯ ВИДОВ ЭКОНОМИЧЕСКОГО АНАЛИЗА
- 172. По характеру использованных показателей:общий экономический анализ;технико-экономический анализ.
- 173. По характеру объектов управления:отраслевой;региональный.
- 174. По субъектам анализа:внутренний управленческий анализ;внешний финансовый анализ.
- 175. По периодичности:годовой;квартальный;месячный;декадный;ежедневный.
- 176. По содержанию:полный;локальный;тематический.
- 177. По времени проведения:перспективный;оперативный;последующий (текущий или ретроспективный).
- 178. Скачать презентанцию
Экономический анализ НаукаСистема специальных знанийОснова - законы развития и функционирования систем Направленность на познание методологии оценки, диагностики и прогнозирования финансово-хозяйственной деятельности предприятия
Слайды и текст этой презентации
Слайд 2Экономический анализ
Наука
Система специальных знаний
Основа - законы развития и функционирования
систем
деятельности предприятияСлайд 3Предмет и объект экономического анализа
Предметом экономического анализа являются причинно-следственные связи
экономических явлений и процессов, познание которых позволяет комплексно исследовать результаты
деятельности.Объектом экономического анализа являются результаты хозяйственной деятельности организации, выраженные системой взаимосвязанных показателей, отражающих отдельные ее стороны.
Слайд 4Принципы
экономического анализа:
научность;
системность;
комплексность;
объективность и конкретность;
действенность;
оперативность;
массовость;
государственный подход;
эффективность.
Слайд 7Методика экономического анализа
Методика экономического анализа - совокупность специфических приемов и
способов, применяемых для обработки экономической информации о работе предприятия.
Методику экономического
анализа принято подразделять на:общую;
частную.
Слайд 11По содержанию:
количественные; Чр, МЗ, ОПФср
качественные.
Вг = ТП/Чр
МО(материалоотдача)= ТП/МЗ
ФО=ТП/ОПФср
Слайд 14Абсолютные показатели
В зависимости от применяемых измерителей абсолютные показатели могут быть:
натуральными;
стоимостными;
трудовыми.
Слайд 15Абсолютные показатели
В зависимости от порядка исчисления абсолютные показатели могут быть:
интервальными;
моментными;
среднехронологическими.
Слайд 16Относительные показатели
В зависимости от характера используемых в расчетах абсолютных показателей
различают следующие относительные показатели:
коэффициенты;
удельные;
структурные.
Слайд 17Относительные показатели
В зависимости от характера используемых в расчетах абсолютных показателей
различают следующие относительные показатели:
коэффициенты; ФО = ТП(руб.)/ОПФср (руб.)
удельные;
структурные.
Слайд 18Относительные показатели
В зависимости от характера используемых в расчетах абсолютных показателей
различают следующие относительные показатели:
коэффициенты; ФО = ТП(руб.)/ОПФср (руб.)
удельные;
Фондовооруженность =
ОПФср (руб.) / Чр(чел.)структурные.
Чр / ППП
Слайд 19Относительные показатели
В зависимости от характера используемых в расчетах абсолютных показателей
различают следующие относительные показатели:
коэффициенты; ФО = ТП(руб.)/ОПФср (руб.)
удельные;
Фондовооруженность =
ОПФср (руб.) / Чр(чел.)структурные.
Чр / ППП
Слайд 23СРАВНЕНИЕ
Сущность сравнения – сопоставление однородных объектов с целью выявления сходства
либо различий между ними.
Слайд 24ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА
горизонтальный сравнительный анализ;
вертикальный сравнительный анализ;
трендовый анализ;
динамические (временные) сравнения;
статические
(пространственные) сравнения;
одномерный сравнительный анализ;
многомерный сравнительный анализ.
Слайд 25ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА
горизонтальный сравнительный анализ – применяется для определения абсолютных
и относительных отклонений фактического уровня исследуемого показателя от базового
Слайд 26ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА
вертикальный сравнительный анализ – предполагает изучение структуры экономических
явлений и процессов путем определения доли частей в общем целом
Слайд 27ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА
трендовый анализ – используется при изучении относительных темпов
роста и прироста показателей за несколько лет к уровню базисного
годаСлайд 28ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА
динамические (временные) сравнения – применяются для изучения изменения
явлений во времени.
Слайд 29ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА
статические (пространственные) сравнения – используются для оценки уровня
показателей одного периода по различным хозяйствующим субъектам
Слайд 30ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА
одномерный сравнительный анализ – проводится сопоставление по одному
или нескольким показателям одного объекта, или сопоставление нескольких объектов по
одному показателю.Слайд 31ВИДЫ СРАВНИТЕЛЬНОГО АНАЛИЗА
многомерный сравнительный анализ – сопоставляются результаты деятельности нескольких
предприятий по широкому спектру показателей.
Слайд 32МНОГОМЕРНЫЙ СРАВНИТЕЛЬНЫЙ АНАЛИЗ
Этап 1.
Обосновывается система показателей, по которым будут оцениваться
результаты хозяйственной деятельности организаций, собираются данные по этим показателям и
формируется матрица исходных данных.Слайд 33МНОГОМЕРНЫЙ СРАВНИТЕЛЬНЫЙ АНАЛИЗ
Этап 2.
Определяется максимальный элемент, который принимается за единицу.
Xij
= Aij / max Aij
Формируется матрица стандартизированных коэффициентов Xij
Слайд 34МНОГОМЕРНЫЙ СРАВНИТЕЛЬНЫЙ АНАЛИЗ
Этап 3. Все элементы матрицы возводятся в квадрат.
Если в задаче указаны веса показателей, то полученные квадраты умножаются
на величину соответствующего весового коэффициента (К), после чего результаты складываются:c применением весового коэффициента:
Rj = K1 * Xij12 + K2 * Xij22 +…+ Kn * Xijn2 ;
без использования весового коэффициента:
Rj = Xij12 + Xij22 +…+ Xijn2 .
Слайд 35МНОГОМЕРНЫЙ СРАВНИТЕЛЬНЫЙ АНАЛИЗ
Этап 4.
Полученные значения рейтинговой оценки (Rj) ранжируются и
определяется рейтинг каждого предприятия.
Слайд 40Детализация по времени позволяет проследить за равномерностью совершения хозяйственных процессов.
Слайд 42Детализация по месту означает разделение общих по предприятию показателей в
разрезе цехов, участков, бригад.
Слайд 44Детализация показателей по составным частям необходима для изучения структуры совокупности
и выявления роли отдельных составных частей в формировании сводных показателей.
Слайд 45
Группировка – деление массы изучаемой совокупности объектов на количественно однородные
группы по соответствующим признакам.
Слайд 47Типологические группировки предназначены для расчленения всей совокупности первичных данных на
однокачественные группы и классы.
Слайд 49Структурные группировки применяются при изучении состава предприятий и структуры выпускаемой
продукции.
Слайд 51Аналитические группировки предназначены для выявления взаимосвязи между анализируемыми экономическими явлениями.
Слайд 54Виды взаимосвязей
детерминированные (функциональные)
Функциональные связи характеризуются строгим соответствием между причиной и
следствием. Каждому значению фактора соответствует одно вполне определенное значение результата.
Слайд 61Виды взаимосвязей
вероятностные (стохастические)
При вероятностных связях между причиной и результатом нет
строгого соответствия, а наблюдается известное соотношение.
Слайд 63Структурно-логическая модель стохастической факторной системы себестоимости продукции земледелия
Слайд 65Аддитивная функциональная зависимость
РП = ВП + Он + И
+ (- Ок) - Н - С
где,РП – реализованная продукция;
ВП - выпуск продукции;
Он,к - остатки нереализованной ТП на начало и конец года;
И , Н - излишки и недостачи , выявленные при инвентаризации;
С - прочие списания продукции.
Слайд 66Мультипликативная функциональная зависимость
ТП= Чр • Д • ч •
Вч
ТП = МЗ*МО
ТП=ОПФ*ФО
Y= a (кол) * b (кач)
Слайд 68Комбинированная функциональная зависимость
П R =
ЗП + МЗ + А + ПРY = a * (b+c)
Y= [a* (b-c)] / z
Слайд 70 Элиминирование представляет собой логический прием
при помощи которого устраняется влияние всех факторов, кроме одного, являющегося
объектом изучения.В экономическом анализе прием элиминирования применяется для определения размера влияния изменений отдельных факторов на изменение результативного показателя.
Слайд 71Элиминирование
Способы элиминирования:
- цепных подстановок;
- абсолютных отклонений;
способ процентных разниц;
индексный;
интегральный.
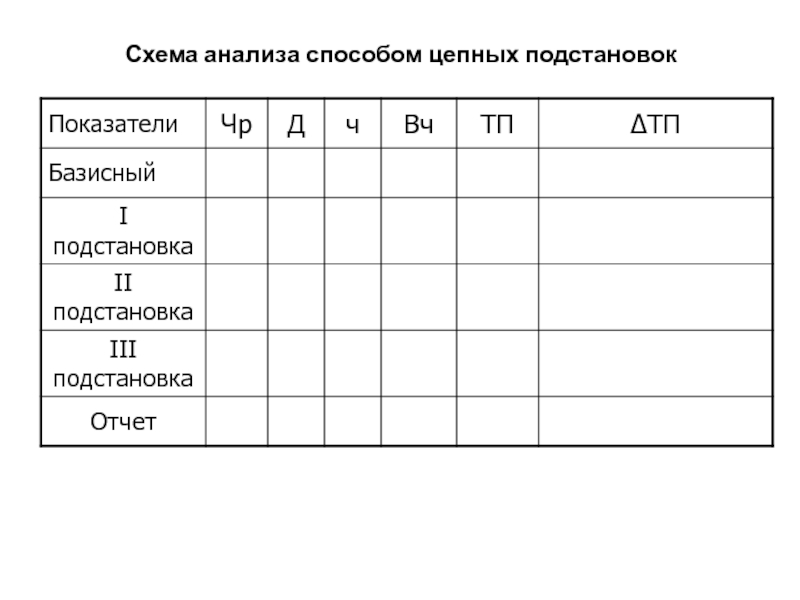
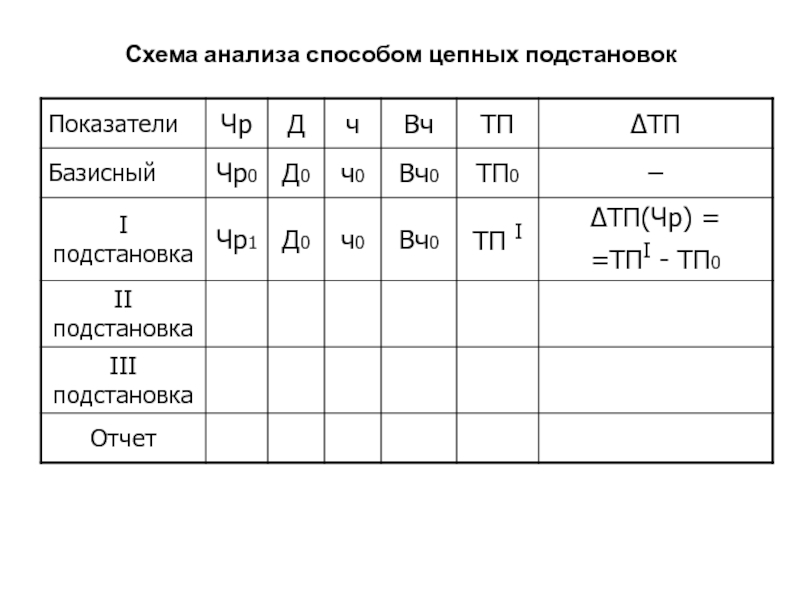
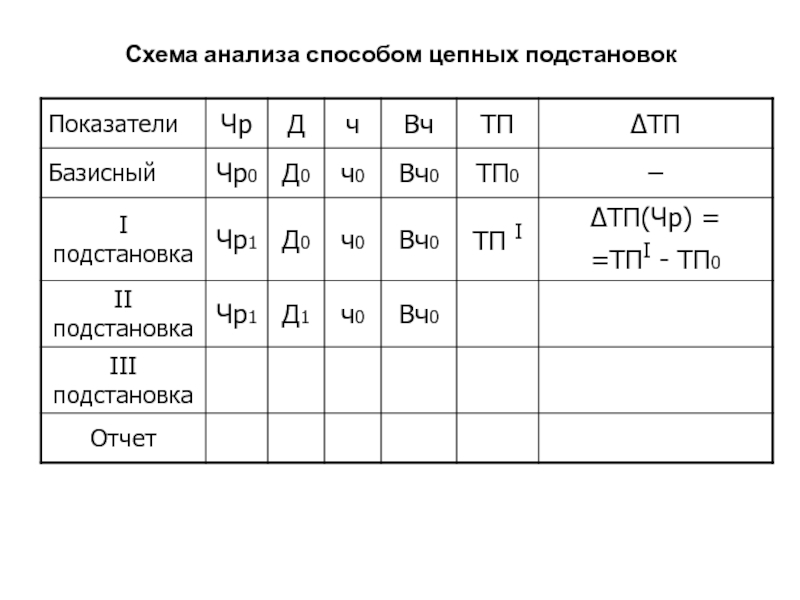
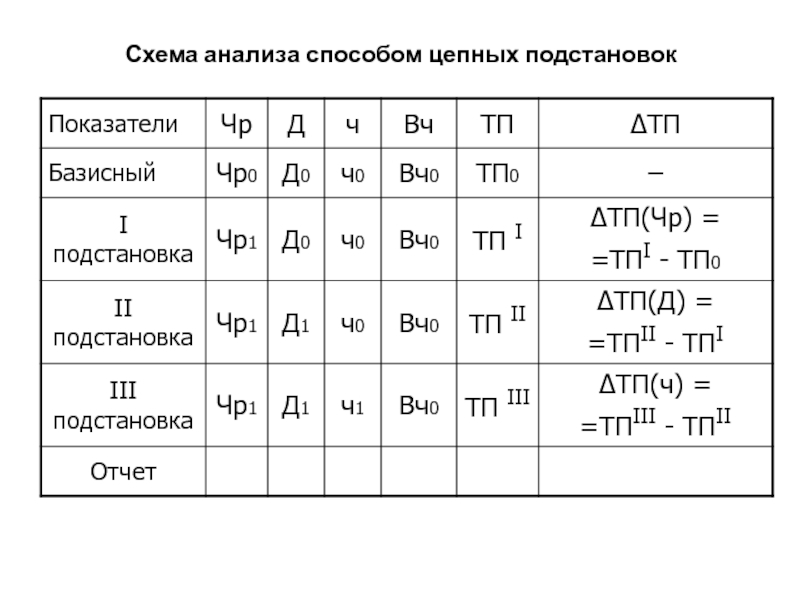
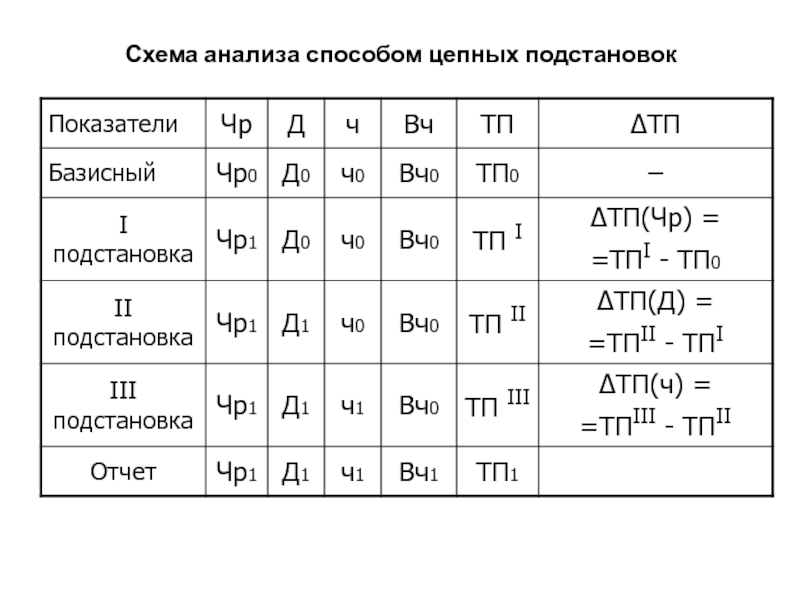
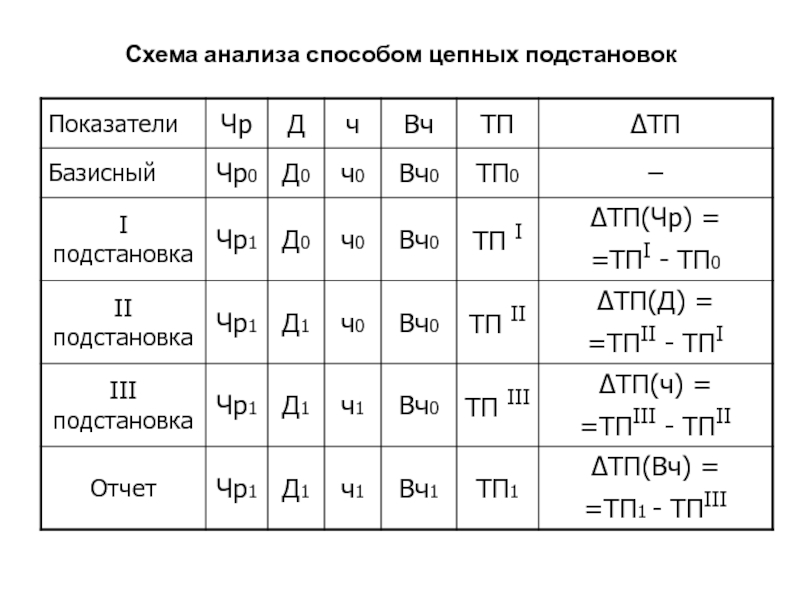
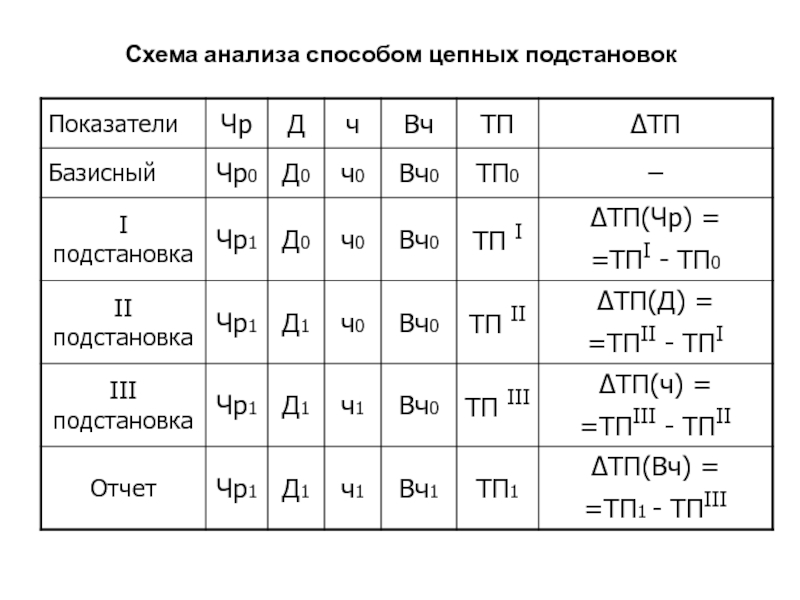
Слайд 75Схема анализа способом цепных подстановок
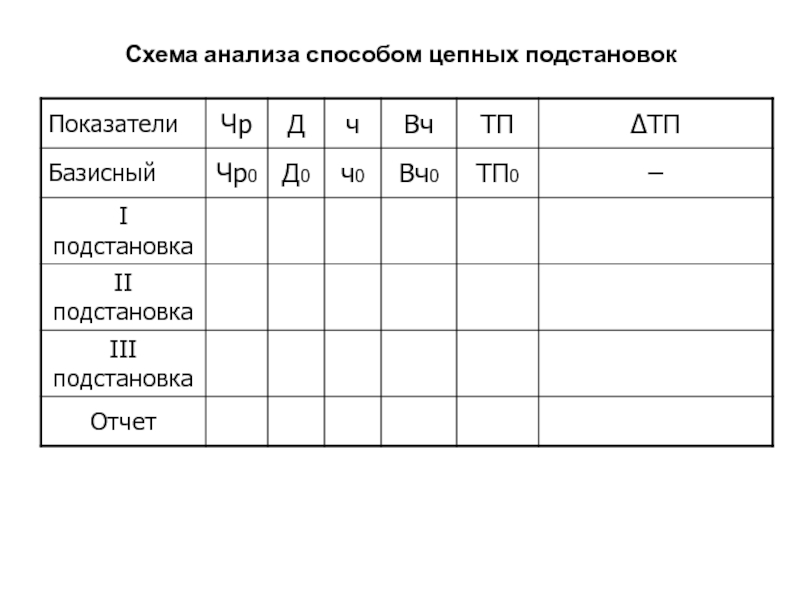
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
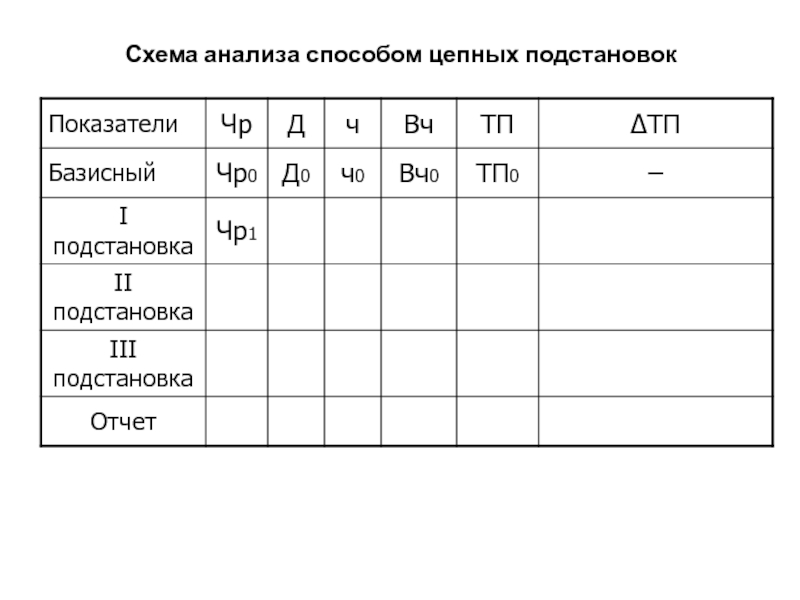
I подстановка
ТП I = Чр1 •
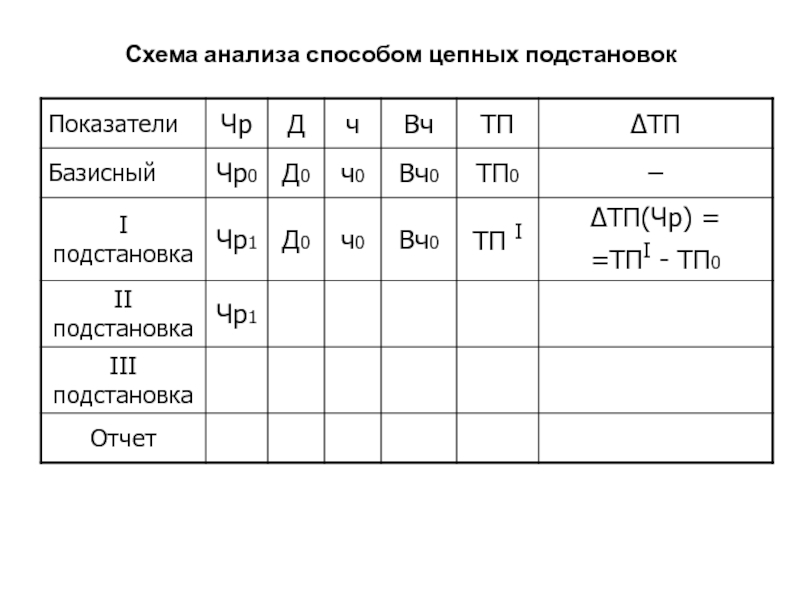
Слайд 76Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
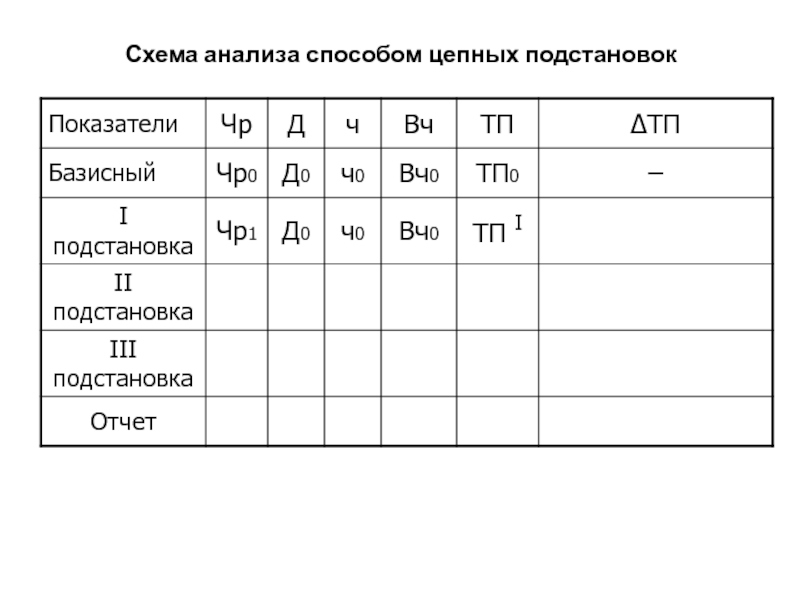
I подстановка
ТП I = Чр1 • Вг0;
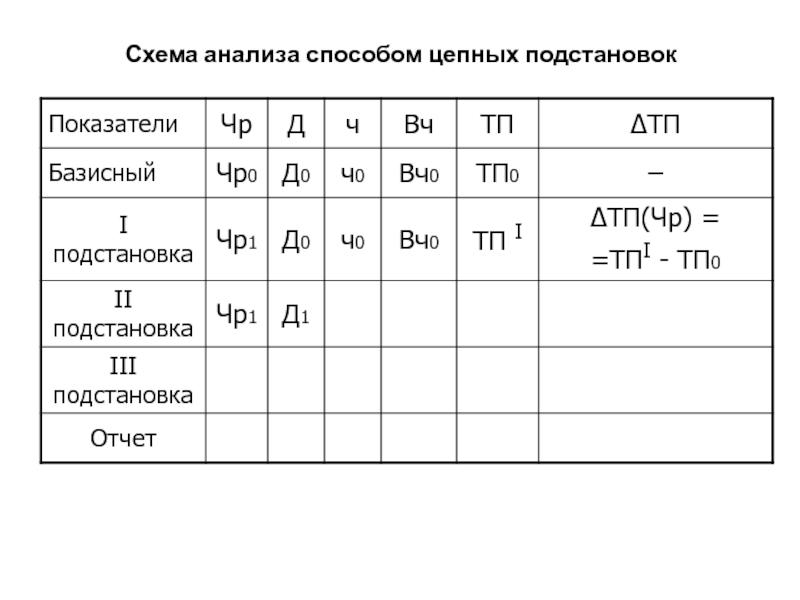
Слайд 77Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
I подстановка
ТП I = Чр1 • Вг0;
∆ТП(Чр)=
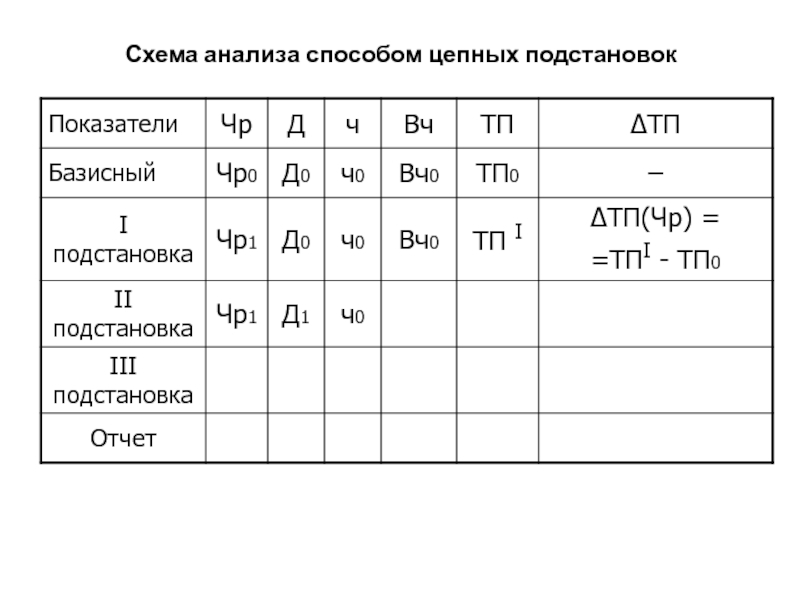
Слайд 78Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
I подстановка
ТП I = Чр1 • Вг0;
∆ТП(Чр)=
Чр1 • Вг0 – Чр0 • Вг0=Слайд 79Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
I подстановка
ТП I = Чр1 • Вг0;
∆ТП(Чр)=
Чр1 • Вг0 – Чр0 • Вг0= ТП I –ТП0; Слайд 80Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
I подстановка
ТП I = Чр1 • Вг0;
∆ТП(Чр)=
Чр1 • Вг0 – Чр0 • Вг0= ТП I –ТП0; ТП1 = Чр1 • Вг1
Слайд 81Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
I подстановка
ТП I = Чр1 • Вг0;
∆ТП(Чр)=
Чр1 • Вг0 – Чр0 • Вг0= ТП I –ТП0; ТП1 = Чр1 • Вг1
∆ТП(Вг)=
Слайд 82Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
I подстановка
ТП I = Чр1 • Вг0;
∆ТП(Чр)=
Чр1 • Вг0 – Чр0 • Вг0= ТП I –ТП0; ТП1 = Чр1 • Вг1
∆ТП(Вг)= Чр1 • Вг1 –
Слайд 83Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
I подстановка
ТП I = Чр1 • Вг0;
∆ТП(Чр)=
Чр1 • Вг0 – Чр0 • Вг0= ТП I –ТП0; ТП1 = Чр1 • Вг1
∆ТП(Вг)= Чр1 • Вг1 – Чр1 • Вг0=
Слайд 84Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
I подстановка
ТП I = Чр1 • Вг0;
∆ТП(Чр)=
Чр1 • Вг0 – Чр0 • Вг0= ТП I –ТП0; ТП1 = Чр1 • Вг1
∆ТП(Вг)= Чр1 • Вг1 – Чр1 • Вг0= ТП1–ТП I
проверка
Слайд 85Схема анализа способом цепных подстановок
ТП= Чр • Вг
ТП0 = Чр0
• Вг0;
I подстановка
ТП I = Чр1 • Вг0;
∆ТП(Чр)=
Чр1 • Вг0 – Чр0 • Вг0= ТП I –ТП0; ТП1 = Чр1 • Вг1
∆ТП(Вг)= Чр1 • Вг1 – Чр1 • Вг0= ТП II –ТП I
проверка
∆ТП = ТП1 – ТП0 =
= ∆ТП(Чр) + ∆ТП(Вг)
Слайд 86Схема анализа способом цепных подстановок
ТП= Чр • Д •
ч • Вч
кол. кол. кол. кач.
ТП=Чр*Вг =
Чр*Д*Вд = Чр*Д*ч*ВчВг =Д*Вд
Вд =ч*Вч
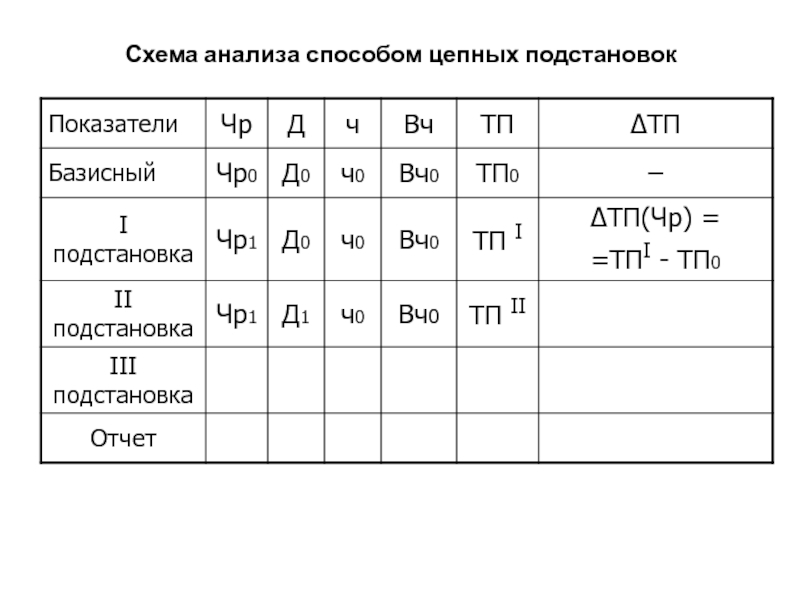
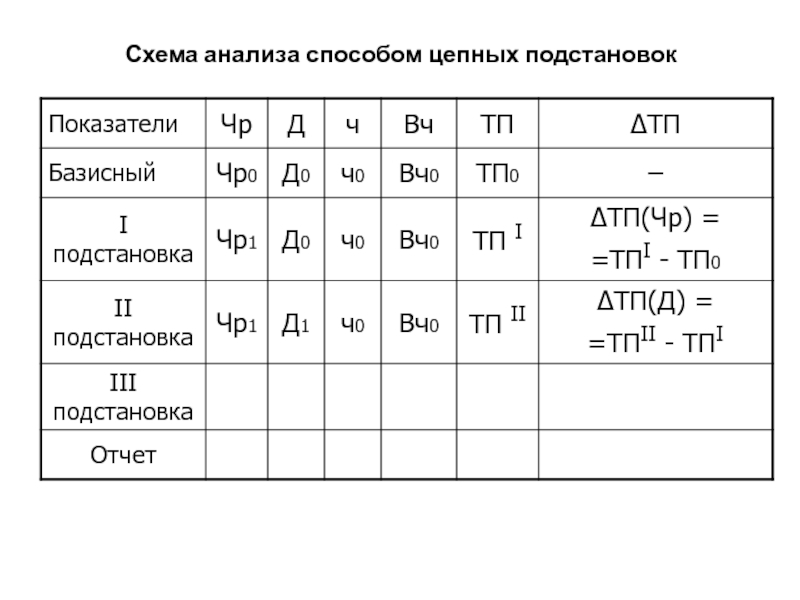
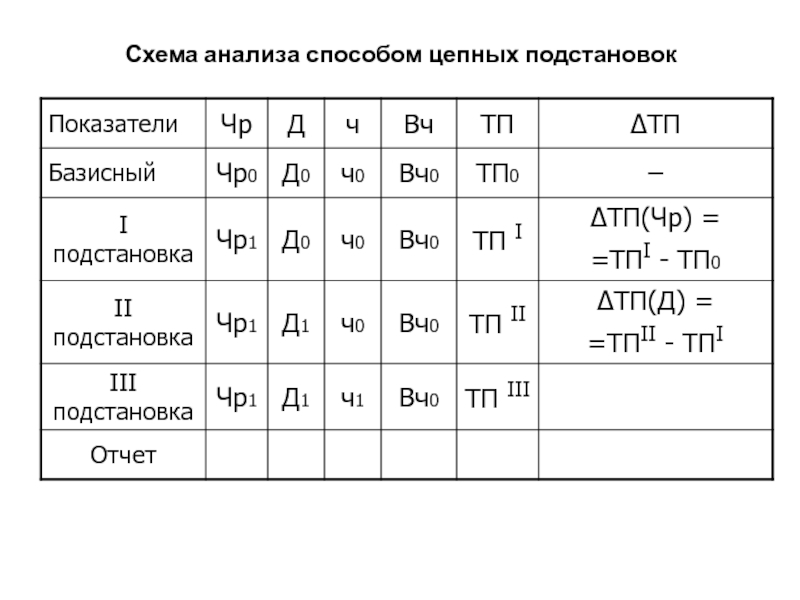
Слайд 87Схема анализа способом цепных подстановок
ТП= Чр • Д •
ч • Вч
кол. кол. кол. кач.
ТП=Чр*Вг =
Чр * Д * Вд = Чр * Д * ч * Вчкол. кол. кач.
Вг= Д * Вд
Вд = ч *Вч
кол. кач.
Слайд 108Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; Слайд 109Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)=
Слайд 110Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1
Слайд 111Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0)
Слайд 112Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
Слайд 113Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
∆ТП(ч)=
Слайд 114Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
∆ТП(ч)= Чр1 •
Слайд 115Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
∆ТП(ч)= Чр1 • Д1 •
Слайд 116Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
∆ТП(ч)= Чр1 • Д1 • (ч1 – ч0)
Слайд 117Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
∆ТП(ч)= Чр1 • Д1 • (ч1 – ч0) • Вч0;
Слайд 118Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
∆ТП(ч)= Чр1 • Д1 • (ч1 – ч0) • Вч0;
∆ТП(Вч)=
Слайд 119Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
∆ТП(ч)= Чр1 • Д1 • (ч1 – ч0) • Вч0;
∆ТП(Вч)= Чр1 • Д1 • ч1 • (Вч1 – Вч0).
Слайд 120Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
∆ТП(ч)= Чр1 • Д1 • (ч1 – ч0) • Вч0;
∆ТП(Вч)= Чр1 • Д1 • ч1 • (Вч1 – Вч0).
проверка
∆ТП = ТП1 - ТП0 =
Слайд 121Схема анализа способом абсолютных отклонений
ТП= Чр • Д • ч
• Вч
∆ТП(Чр)= (Чр1 – Чр0) • Д0 • ч0 •
Вч0; ∆ТП(Д)= Чр1 • (Д1 – Д0) • ч0 • Вч0;
∆ТП(ч)= Чр1 • Д1 • (ч1 – ч0) • Вч0;
∆ТП(Вч)= Чр1 • Д1 • ч1 • (Вч1 – Вч0).
проверка
∆ТП = ТП1 - ТП0 =
= ∆ТП(Чр) + ∆ТП(Д) + ∆ТП(ч) + ∆ТП(Вч)
Слайд 147Схема анализа индексным способом
ТП= Чр • Д • ч •
Вч
IЧр= Чр1•Д0•ч0•Вч0/Чр0•Д0•ч0•Вч0;
IД= Чр1•Д1•ч0•Вч0/Чр1•Д0•ч0•Вч0;
Iч= Чр • Д • ч • Вч
/ Чр • Д • ч • ВчСлайд 148Схема анализа индексным способом
ТП= Чр • Д • ч •
Вч
IЧр= Чр1•Д0•ч0•Вч0/Чр0•Д0•ч0•Вч0;
IД= Чр1•Д1•ч0•Вч0/Чр1•Д0•ч0•Вч0;
Iч= Чр1•Д1•ч1•Вч0/Чр1•Д1•ч0•Вч0;
Слайд 149Схема анализа индексным способом
ТП= Чр • Д • ч •
Вч
IЧр= Чр1•Д0•ч0•Вч0/Чр0•Д0•ч0•Вч0;
IД= Чр1•Д1•ч0•Вч0/Чр1•Д0•ч0•Вч0;
Iч= Чр1•Д1•ч1•Вч0/Чр1•Д1•ч0•Вч0;
IВч= Чр1•Д1•ч1•Вч1/Чр1•Д1•ч1•Вч0;
Слайд 150Схема анализа индексным способом
ТП= Чр • Д • ч •
Вч
IЧр= Чр1•Д0•ч0•Вч0/Чр0•Д0•ч0•Вч0;
IД= Чр1•Д1•ч0•Вч0/Чр1•Д0•ч0•Вч0;
Iч= Чр1•Д1•ч1•Вч0/Чр1•Д1•ч0•Вч0;
IВч= Чр1•Д1•ч1•Вч1/Чр1•Д1•ч1•Вч0;
проверка
I ТП = ТП1/ТП0 =
=Чр1•Д1•ч1•Вч1/Чр0•Д0•ч0•Вч0 =
Слайд 151Схема анализа индексным способом
ТП= Чр • Д • ч •
Вч
IЧр= Чр1•Д0•ч0•Вч0 / Чр0•Д0•ч0•Вч0;
IД= Чр1•Д1•ч0•Вч0 / Чр1•Д0•ч0•Вч0;
Iч= Чр1•Д1•ч1•Вч0 / Чр1•Д1•ч0•Вч0;
IВч=
Чр1•Д1•ч1•Вч1 / Чр1•Д1•ч1•Вч0;проверка
I ТП = ТП1/ТП0 =
=Чр1•Д1•ч1•Вч1/Чр0•Д0•ч0•Вч0 =
= IЧр• IД •Iч •IВч
Слайд 155Схема анализа интегральным способом
ТП= Чр • Вг
∆ТП(Чр)= ∆Чр • Вг0
+ 0,5 • ∆Чр • ∆Вг;
∆ТП(Вг)= ∆Вг • Чр0 +
Слайд 156Схема анализа интегральным способом
ТП= Чр • Вг
∆ТП(Чр)= ∆Чр • Вг0
+ 0,5 • ∆Чр • ∆Вг;
∆ТП(Вг)= ∆Вг • Чр0 +
0,5 • ∆Чр • ∆Вг.Слайд 157Схема анализа интегральным способом
ТП= Чр • Вг
∆ТП(Чр)= ∆Чр • Вг0
+ 0,5 • ∆Чр • ∆Вг;
∆ТП(Вг)= ∆Вг • Чр0 +
0,5 • ∆Чр • ∆Вг.проверка
∆ТП = ТП1 - ТП0 =
= ∆ТП(Чр) + ∆ТП(Вг)
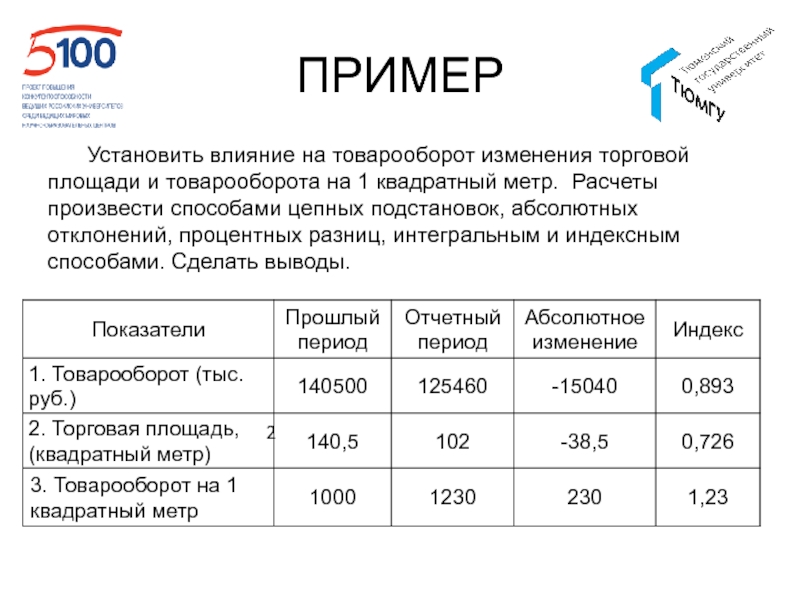
Слайд 158ПРИМЕР
Установить влияние на товарооборот изменения торговой площади и товарооборота на
1 квадратный метр. Расчеты произвести способами цепных подстановок, абсолютных отклонений,
процентных разниц, интегральным и индексным способами. Сделать выводы.2
Слайд 159ПРИМЕР
ТО1м.кв. =ТО / Тп
ТО = Тп * ТО1м.кв.
ТО0 = Тп0
* ТО1м.кв.0 = 140500 (тыс. руб.)
ТО = Тп1 * ТО1м.кв.0
= 102 * 1000 = 102000 (тыс. руб.)∆ТО(Тп) = Тп1 * ТО1м.кв.0 – Тп0 * ТО1м.кв.0 =
= ТО - ТО0 = 102000 – 140500 = -38500 (тыс. руб.)
ТО1 = Тп1 * ТО1м.кв.1 = 125460 (тыс. руб.)
∆ТО(ТО1м.кв.1 ) = Тп1 * ТО1м.кв.1 – Тп1 * ТО1м.кв.0 =
= ТО1 – ТО = 125460 – 102000 = 23460 (тыс. руб.)
∆ТО = ТО1 – ТО0 = ∆ТО(Тп) + ∆ТО(ТО1м.кв.1 ) =-38500 +23460 =
= -15040 (тыс. руб.)
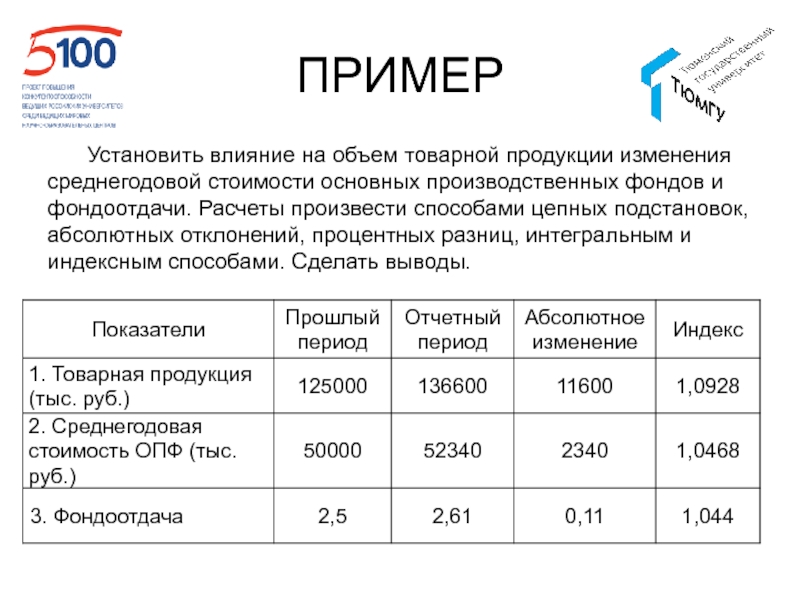
Слайд 160ПРИМЕР
Установить влияние на объем товарной продукции изменения среднегодовой стоимости основных
производственных фондов и фондоотдачи. Расчеты произвести способами цепных подстановок, абсолютных
отклонений, процентных разниц, интегральным и индексным способами. Сделать выводы.Слайд 165ПРИМЕР
ТП0= ОПФ0 * ФО0 =50000 * 2,5 = 125000 тыс.
руб.
ТП = ОПФ1 * ФО0 = 52340 * 2,5 =
130850 тыс.руб.∆ТП(ОПФ)= ТП - ТП0 = 130850 – 125000 = 5850 тыс. руб.
ТП1 = ОПФ1 * ФО1 = 52340 * 2,61 = 136600 тыс. руб.
∆ТП(ФО)= ТП1 – ТП = 136600 – 130750 = 5750 тыс. руб.
∆ТП = ТП1 – ТП0= ∆ТП(ОПФ) +∆ТП(ФО) = 11600 тыс. руб.
Слайд 166ПРИМЕР
∆ТП(ОПФ)= (ОПФ1 – ОПФ0) * ФО0 = 2340 * 2,5
= 5850 тыс. руб.
∆ТП(ФО)= ОПФ1 *(ФО1 - ФО0) =
52340 * 0,11 = 5757,4 тыс. руб.∆ТП = ТП1 – ТП0= ∆ТП(ОПФ) +∆ТП(ФО)
5850+5757,4 = 136600-125000 = 11607,4 тыс. руб. 11600 тыс. руб.
Слайд 167ПРИМЕР
∆ТП(ОПФ)= (ОПФ1 – ОПФ0) * ФО0 = 800 * 3,125
= 2500 (тыс. руб.)
∆ТП(ФО)= ОПФ1 *(ФО1 - ФО0) =
4000 * 0,875 = 3500 (тыс. руб.)∆ТП = ТП1 – ТП0= ∆ТП(ОПФ) +∆ТП(ФО)
16000 -10000 = 2500 +3500 = 6000
Слайд 168ПРИМЕР
ТП = ОПФ * ФО
∆ТП(ОПФ)= (IОПФ – 1) * ТП0
= (1,25 – 1) * 10000 = 2500 (тыс. руб.)
∆ТП(ФО)=
(IТП – IОПФ)* ТП0 = (1,6-1,25)*10000 = 3500 (тыс. руб.)∆ТП = ТП1 – ТП0= ∆ТП(ОПФ) +∆ТП(ФО)
16000 -10000 = 2500 +3500 = 6000
Слайд 169ПРИМЕР
ТП = ОПФ * ФО
IОПФ = ( ОПФ1 * ФО0
) / ( ОПФ0 * ФО0 ) = 1,25
IФО= (
ОПФ1 * ФО1 ) / ( ОПФ1 * ФО0 ) = 1,28IТП= ТП 1 / ТП 0 = 1,6 = IОПФ * IФО = 1,25 * 1,28 = 1,6
Слайд 170ПРИМЕР
ТП = ОПФ * ФО
∆ТП(ОПФ)=∆ОПФ * ФО0 + 0,5* ∆ОПФ
* ∆ФО = 800 * 3,125 + + 0,5*800*0,875
= 2850 (тыс. руб.)∆ТП(ФО)= ∆ФО * ОПФ0 + 0,5* ∆ОПФ * ∆ФО = 3150 (тыс. руб.)
∆ТП = ТП1 – ТП0= ∆ТП(ОПФ) +∆ТП(ФО)
16000 -10000 = 2850 +3150 = 6000