Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория игр
Содержание
- 1. Теория игр
- 2. Предмет изучения Теория игр – раздел теории
- 3. Основные понятия теории игрКонфликтной называется ситуация,
- 4. Игроки – заинтересованные стороны в игре (участники
- 5. Будем предполагать, что каждый из участников парной
- 6. Функция выигрыша – степень удовлетворения интересов игрока
- 7. Предполагается, что игра происходит по определенным правилам
- 8. Цель теории игр – выработка рекомендаций для
- 9. Замечания: Выбор оптимальной стратегии базируется
- 10. Парная игра с нулевой суммой выигрышаОпределение. Игры,
- 11. Пусть игроки А и В имеют наборы
- 12. Платежная матрицаА = Аналогичным образом можно построить
- 13. Замечания. Матрица игры существенно зависит от упорядочивания
- 14. Максиминные и минимаксные
- 15. РЕЗУЛЬТАТ: игрок А выберет ту стратегию, при
- 16. Анализ платежной матрицы : игрок В
- 17. Объединим результаты анализа для игроков Т.к.α2=α3, то
- 18. Игра с седловой точкойНижняя цена (4) игры
- 19. Уменьшение размерности игры
- 20. Слайд 20
- 21. Слайд 21
- 22. Приведение матричной игры к задаче линейного программирования
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Скачать презентанцию
Предмет изучения Теория игр – раздел теории исследования операций, изучающий формальные модели принятия оптимальных решений в конфликтных ситуациях.Математическая модель конфликтной ситуации называется игрой.
Слайды и текст этой презентации
Слайд 2Предмет изучения
Теория игр – раздел теории исследования операций, изучающий
формальные модели принятия оптимальных решений в конфликтных ситуациях.
ситуации называется игрой.Слайд 3Основные понятия теории игр
Конфликтной называется ситуация, в которой взаимодействует
несколько сторон, и при этом каждый из участников старается достичь
своей цели доступным ему способом, а результат взаимодействия зависит от действий каждого участника.Черты конфликтной ситуации:
наличие заинтересованных сторон
наличие своих интересов (целей) у каждой стороны
наличие набора возможных действий у каждой из сторон
часто недостаток информации (неопределенность)
ПРИМЕРЫ
Покупатель и продавец
Работник и работодатель
Спортивные состязания
Вооруженные конфликты
Слайд 4Игроки – заинтересованные стороны в игре (участники игры).
Парная игра –
игра, в которой принимают участие два игрока.
Множественная игра –
игра с числом участников более двух.Коалиция - объединение игроков
коалиции действия, коалиции интересов
Стратегия – любое возможное действие (комплекс действий) игрока
Ход - выбор действия игроками (личный ход *)
Ситуация (исход игры) – состояние, в котором оказываются игроки после очередного хода
Слайд 5Будем предполагать, что каждый из участников парной игры обладает своим
набором чистых стратегий: SA={A1,A2,…,Am}, SB={B1,B2,…,Bn}
В условиях конфликта каждый
игрок делает свой ход, т.е. выбирает одну из своих возможных стратегий.Сделав ход, игроки оказываются в ситуации Хij={Ai, Bj}.
Правила игры могут запрещать отдельные ситуации, которые называются «запрещенными».
Если в процессе игры возникает запрещенная ситуация, то игра считается несостоявшейся.
Слайд 6Функция выигрыша – степень удовлетворения интересов игрока (FA).
Функция выигрыша определена
на множестве ситуаций (SA, SB) и ставит в соответствие каждой
ситуации Xij некоторое число F(Xij), называемое выигрышем игрока А в данной ситуации.Реализация игры – выбор игроками своих возможных стратегий и получение в сложившейся ситуации своего выигрыша.
Слайд 7Предполагается, что игра происходит по определенным правилам (без этого не
возможна формализация задачи).
Правила - система условий, которые описывают:
возможные действия каждого
из игроков;объем информации, которую может получить каждая из сторон о возможных действиях противника;
исход (результат) игры после каждой совокупности «ходов» противника
Слайд 8Цель теории игр – выработка рекомендаций для удовлетворительного поведения игроков
в конфликте и выявления для каждого из них оптимальной стратегии.
Оптимальная
стратегия – такая стратегия, которая при многократном повторении игры гарантирует игроку максимальный возможный средний выигрыш (при условии неопределенности –не зависящий от поведения других участников).Слайд 9
Замечания:
Выбор оптимальной стратегии базируется на принципе разумности каждого игрока, т.е.
поведение каждого из них направлено на достижение своих целей.
Оптимальность опирается
на некоторый критерий. Поэтому возможны случаи, когда стратегия является оптимальной в смысле одного критерия и не оптимальной в смысле другого.Слайд 10Парная игра с нулевой суммой выигрыша
Определение. Игры, в которых каждый
из игроков преследует противоположные интересы называются антагонистическими.
В антагонистической игре один
из игроков выигрывает ровно столько, сколько проигрывает другой.Следовательно: FA(AiBj) = - FB(BjAi) или
FA(AiBj) + FB(BjAi) = 0
Антагонистическая парная игра определяется совокупностью {SA, SB, FA}
Слайд 11Пусть игроки А и В имеют наборы стратегий SA={A 1
A2,…,Am} и SB={B1,B2,…,Bn}.
Cитуация Хij=(Ai, Bj) полностью определяет выигрыш игрока А,
который равен значению функции выигрыша FА(AiBj)= aij. Это число в антагонистической парной игре одновременно проигрыш игрока В.
Матрица А={aij}, в которой номер строки - номер стратегии игрока А, а номер столбца – номер стратегии игрока В, называется матрицей выигрыша игрока А.
Слайд 12Платежная матрица
А =
Аналогичным образом можно построить матрицу выигрышей игрока
В.
При этом В= - АТ.
Таким образом матрица В
полностью определяется матрицей А.
Матрица А называется также платежной матрицей или матрицей игры.
Слайд 13Замечания.
Матрица игры существенно зависит от упорядочивания множеств SA и
SB. При иной нумерации стратегий матрица окажется другой. Т.е. одна
и та же игра может быть представлена различными матрицами. Но функция FA остается однозначно определенной.Построение матрицы игры является весьма сложной задачей. Однако, всякую конечную игру можно привести к матричной форме.
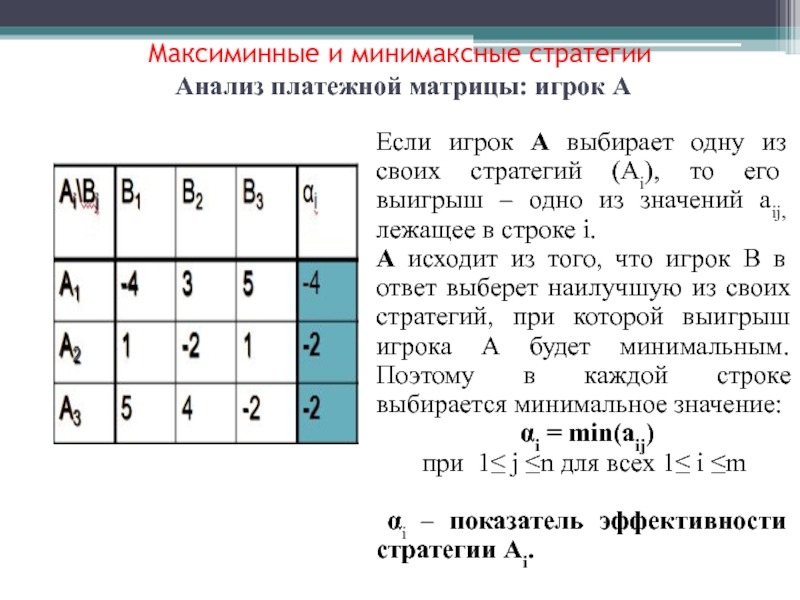
Слайд 14 Максиминные и минимаксные стратегии Анализ платежной матрицы:
игрок А
Если игрок А выбирает одну из своих стратегий (Аi),
то его выигрыш – одно из значений aij, лежащее в строке i.А исходит из того, что игрок В в ответ выберет наилучшую из своих стратегий, при которой выигрыш игрока А будет минимальным. Поэтому в каждой строке выбирается минимальное значение:
αi = min(aij)
при 1≤ j ≤n для всех 1≤ i ≤m
αi – показатель эффективности стратегии Аi.
Слайд 15РЕЗУЛЬТАТ: игрок А выберет ту стратегию, при которой показатель эффективности
αi принимает максимальное значение:
α =max(αi ) = max
min(aij) при 1≤ j ≤n и 1≤ i ≤m.Данный принцип выбора стратегии называется максиминным.. Число α – нижняя цена игры.
Число α, максимин стратегий игрока А, показывает гарантированный выигрыш А, не зависящий от выбора стратегии игроком В.
SAmaxmin – множество максиминных стратегий игрока А
Анализ платежной матрицы: игрок А
Слайд 16
Анализ платежной матрицы : игрок В
В антагонистической игре результат игры
для игрока В удобно анализировать как «проигрыш». Для стратегий Вj
значения «функции проигрыша» расположены в столбцах матрицы FA: aji.Максимальный выигрыш игрока А : βj = max(aji) при 1≤ i ≤m.
Интерес игрока В: выбрать такую стратегию, при которой игрок А будет иметь минимальный выигрыш:
β = min(βj ) = minmax(aji)
Это минимаксный принцип, а число
β – верхняя цена игры.
Слайд 17Объединим результаты анализа для игроков
Т.к.α2=α3, то стратегии
А2 и
А3 – максиминные стратегии игрока А.
У игрока В стратегия В2
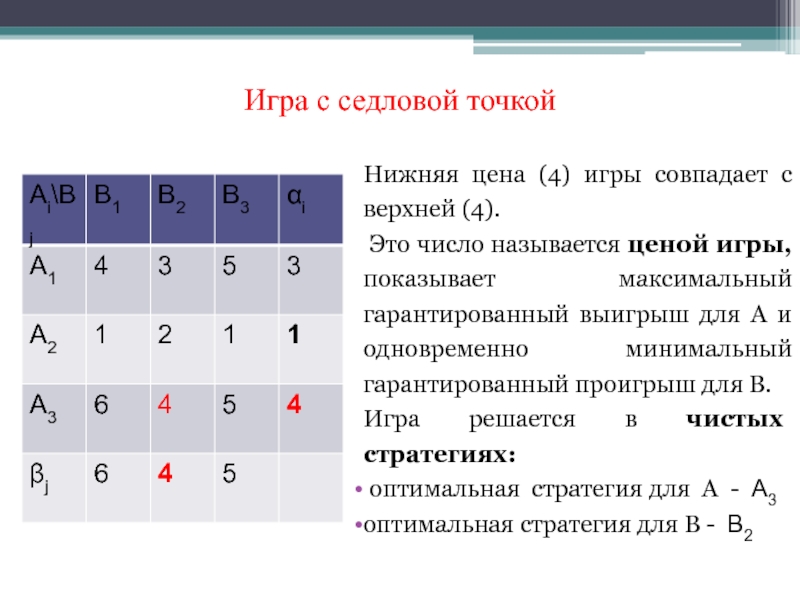
минимаксная.Слайд 18Игра с седловой точкой
Нижняя цена (4) игры совпадает с верхней
(4).
Это число называется ценой игры, показывает максимальный гарантированный выигрыш
для А и одновременно минимальный гарантированный проигрыш для В.Игра решается в чистых стратегиях:
оптимальная стратегия для А - A3
оптимальная стратегия для В - B2