Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРИЯ МНОЖЕСТВ БИНАРНЫЕ ОТНОШЕНИЯ. ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ ЛЕКЦИЯ 4
Содержание
- 1. ТЕОРИЯ МНОЖЕСТВ БИНАРНЫЕ ОТНОШЕНИЯ. ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ ЛЕКЦИЯ 4
- 2. Цель лекции – изучить свойства бинарных отношений,
- 3. Литература Горбатов В.А. Основы дискретной математики. М.:
- 4. ТерминыБазовые понятия: множество подмножество упорядоченная пара вектор
- 5. Def: бинарным (двухместным) отношением на множестве M
- 6. Способы задания бинарных отношений. 11. Матрица смежностиDef:
- 7. Способы задания бинарных отношений. 22. ГрафDef: граф
- 8. V={a, b, c, d, e}, ТV2a –
- 9. Историческая справкаДжон фон Нейман Американский математик Доктор
- 10. Способы задания бинарных отношений. 33. Фактор-множествоDef: окрестность
- 11. РефлексивностьRA2 – рефлексивно, еслиai A
- 12. 3. ТранзитивностьRA2 – транзитивно, еслиai,aj,ak A :
- 13. Бинарное отношение эквивалентности Обозначение: R~ Граф Рефлексивность: xx Симметричность: xyyx Транзитивность: xy, yz xz Пример
- 14. Разбиение множества Def: разбиение Г множества А
- 15. Процедура построения разбиения множества Пусть на множестве
- 16. Классы эквивалентностиПостроенная система классов обладает следующими свойствами:
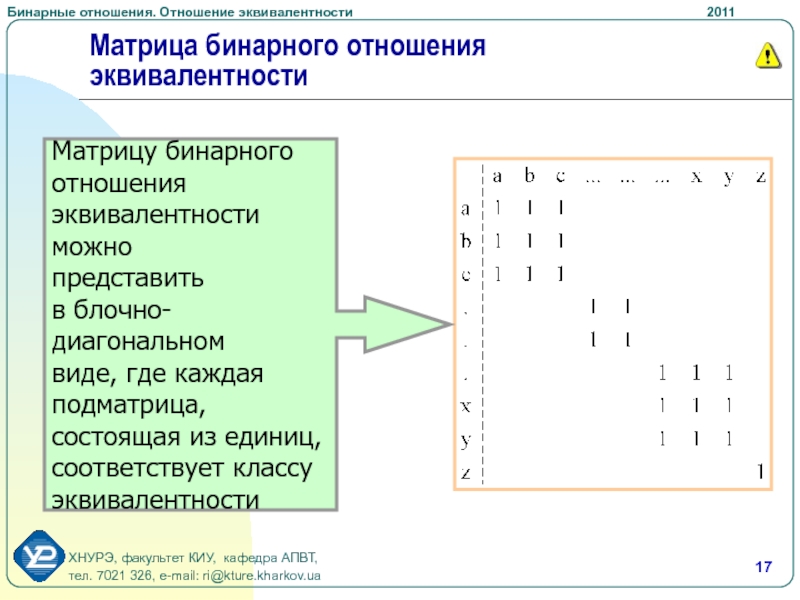
- 17. Матрица бинарного отношения эквивалентностиМатрицу бинарного отношения эквивалентности
- 18. Выводы. 1При исследовании возникает задача выбора существенных
- 19. Выводы. 2 Если моделируемый объект представлен в
- 20. Тест-вопросы1. Какое из отношений является бинарным:а) RM3;
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ТЕОРИЯ МНОЖЕСТВ
БИНАРНЫЕ ОТНОШЕНИЯ. ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ
ЛЕКЦИЯ 4
Факультет компьютерной инженерии и
управления, кафедра АПВТ, ХНУРЭ
Слайд 2Цель лекции – изучить свойства бинарных отношений, способы их задания
для применения в задачах компьютерной инженерии
Содержание:
Определение бинарного отношения
Способы задания бинарных отношенийСвойства бинарных отношений
Бинарное отношение эквивалентности
Классы эквивалентности
Применение в задачах компьютерной инженерии
Тема: Бинарные отношения.
Отношение эквивалентности
Слайд 3Литература
Горбатов В.А. Основы дискретной математики. М.: Высш. шк., 1986.
10-14 с.
Лавров И.А., Максимова Л.Л. Задачи по теории множеств,
математической логике и теории алгоритмов. М.: Наука. Главная редакция физико-математической литературы, 1984. 224 с.Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. М.: Энергия, 1980. 344 с.
Богомолов А.М., Сперанский Д.В. Аналитические методы в задачах контроля и анализа дискретных устройств. Саратов: Изд-во Саратовкого ун-та, 1986. 240с.
Новиков Ф.А. Дискретная математика для программистов. С.-П., 2001. С. 4-24.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. 12-16 с.
Слайд 4Термины
Базовые понятия:
множество
подмножество
упорядоченная пара
вектор
декартово произведение
декартова степень
отношение
Ключевые слова:
бинарное отношение
матрица смежности
граф
фактор-множество
рефлексивностьсимметричность
транзитвность
отношение эквивалентности
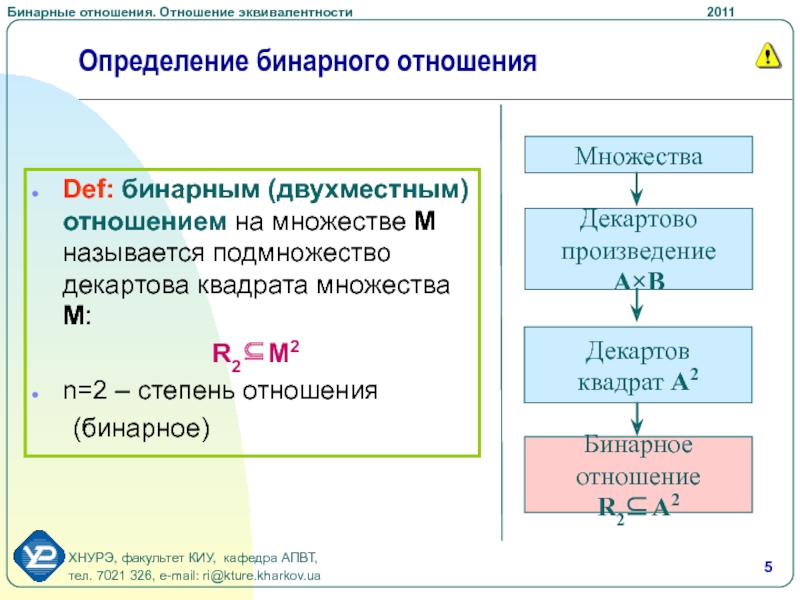
Слайд 5Def: бинарным (двухместным) отношением на множестве M называется подмножество декартова
квадрата множества М:
R2М2
n=2 – степень отношения
(бинарное)
Определение бинарного отношения
Слайд 6Способы задания бинарных отношений. 1
1. Матрица смежности
Def: матрица смежности
бинарного отношения
на
множестве А={а1, а2, а3, …¾, an} –
это таблица размера nn,
в которой элемент cij ,
определяется следующим образом:
Пример
Дано: А={а, b},
R2={(a,a), (b,a)} A2
Матрица смежности
бинарного отношения
R2 представляется так:
Слайд 7Способы задания бинарных отношений. 2
2. Граф
Def: граф – это совокупность
множества V с заданным на нем отношением UV2:
G=
V
– носитель графа (множество вершин), U – сигнатура графа (множество ребер или дуг).
Пример
Дано: А={а, b},
R2={(a,a), (b,a)} A2
Граф бинарного
отношения R2
изображается так:
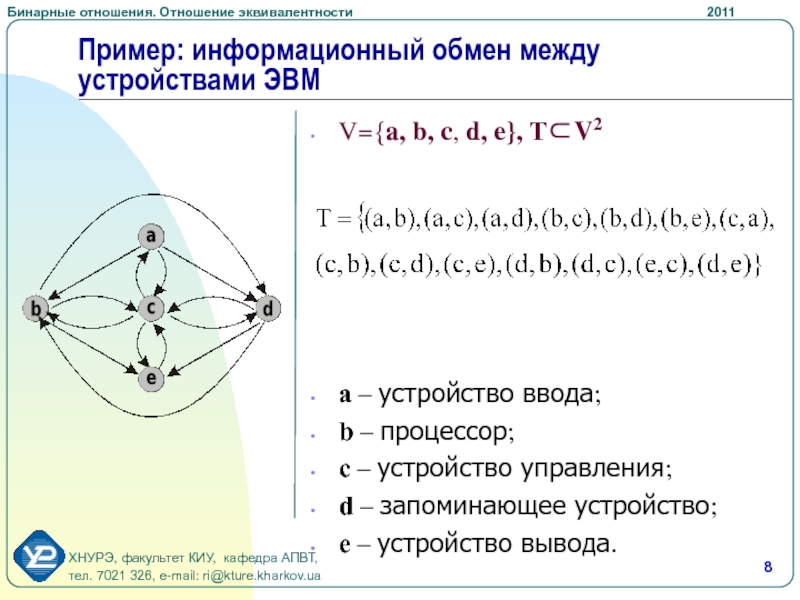
Слайд 8V={a, b, c, d, e}, ТV2
a – устройство ввода;
b
– процессор;
c – устройство управления;
d – запоминающее устройство;
e – устройство вывода.
Пример: информационный обмен между устройствами ЭВМ
Слайд 9Историческая справка
Джон фон Нейман
Американский математик
Доктор физико-математических наук
Член Национальной Академии наук США
Профессор Принстонского университета
в США с 1933Член Комиссии по атомной энергии США с 1954
Директор Бюро по проектированию ЭВМ (1945-1955)
Слайд 10Способы задания бинарных отношений. 3
3. Фактор-множество
Def: окрестность единичного
радиуса элемента
aiA :
O(ai)={ aj | (ai,aj)RA2, ajA }
Def: фактор-множество A/R
(или
A|R) множества À по отношению RA2 есть
совокупность окрестностей
единичного радиуса
A/R = { O(ai) | aiA }
Пример
a b c d e
{b,c,d}{c,d,e}{a,b,d,e}{b,c,а}{c}
Верхняя строка – элементы множества À
Нижняя – совокупность окрестностей единичного радиуса элементов ai
Слайд 11 Рефлексивность
RA2 – рефлексивно, если
ai A (ai,ai)RA2
матрица смежности имеет
единичную главную диагональ:
в графе – петли:
2. Симметричность
RA2 – симметрично, еслиai, aj A : (ai,aj)R (aj,ai)RA2
матрица смежности симметрична относительно главной диагонали:
в графе – симметрично направленные дуги:
Свойства бинарных отношений. 1
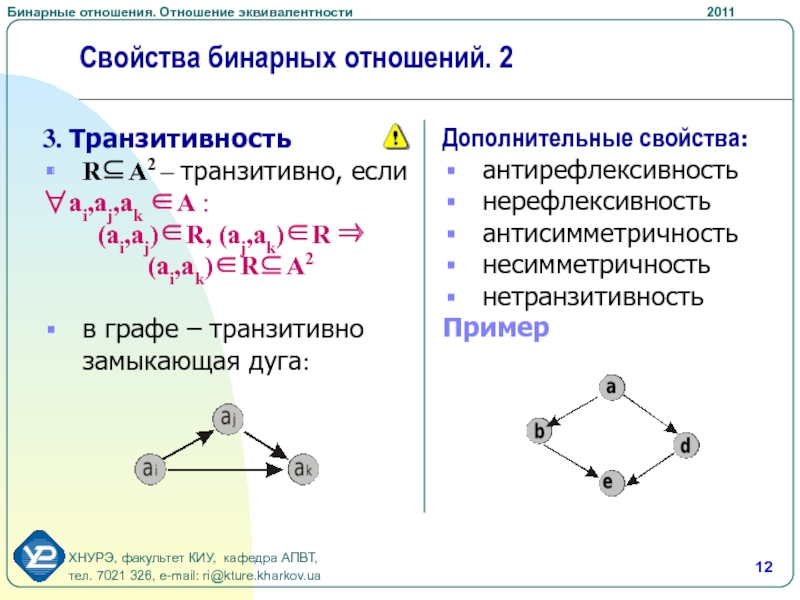
Слайд 123. Транзитивность
RA2 – транзитивно, если
ai,aj,ak A :
(ai,aj)R, (aj,ak)R
(ai,ak)RA2
в
графе – транзитивно замыкающая дуга:
Дополнительные свойства:
антирефлексивность
нерефлексивность
антисимметричность
несимметричность
нетранзитивность
Пример
Свойства бинарных отношений. 2
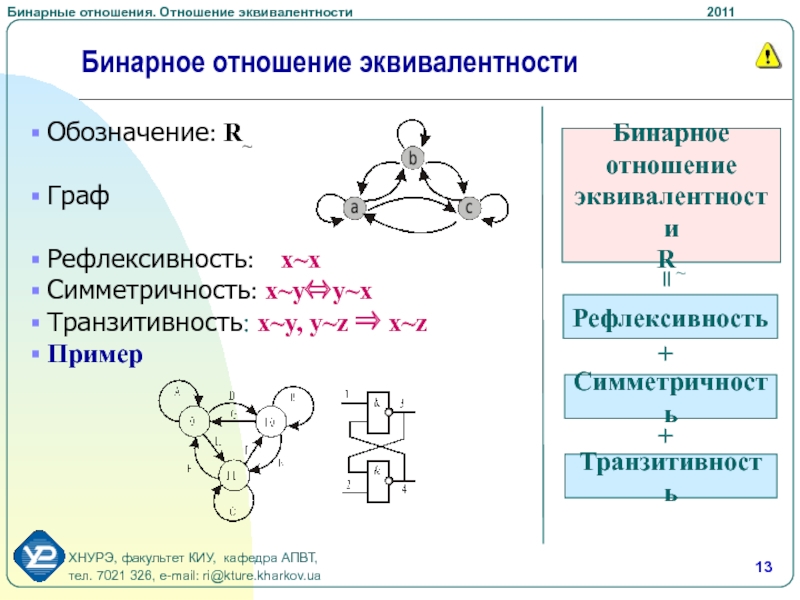
Слайд 13Бинарное отношение эквивалентности
Обозначение: R~
Граф
Рефлексивность: xx
Симметричность: xyyx
Транзитивность: xy, yz xz
Пример
Слайд 14Разбиение множества
Def: разбиение Г множества А – семейство непустых
попарно непересекающихся подмножеств, объединение которых совпадает с А
Свойства ГВ(А)
KiÃ: Ki Ki, Kj Г: KiKj =
Пример
Для трехэлементного множества
A={a,b,c} разбиениями являются
Г1={ {a, b, c} }
Г2={ {a}, {b}, {c} }
Г3={ {a}, {b,c} }
Г4={ {b}, {a,c} }
Г5={ {c}, {a,b} }
Слайд 15Процедура построения разбиения множества
Пусть на множестве А задано отношение
эквивалентности R~
Выберем элемент a1A и образуем подмножество (класс) K1A,
состоящий из элемента а1 и всех элементов, эквивалентных ему:Выберем элемент a2A, а2а1, и образуем подмножество (класс) K2A, состоящий из элемента а2 и всех элементов, эквивалентных ему:
Таким образом, получаем систему классов, объединение которых совпадает с множеством А
Слайд 16Классы эквивалентности
Построенная система классов обладает следующими свойствами:
образует разбиение
любые
два элемента из одного класса эквивалентны
любые два элемента из
разных классов не эквивалентныDef: класс эквивалентности [à] элемента à
[a]={ x | xa, xA }
Свойства классов эквивалентности:
a[a]
b[a][b]=[a]
[a][b]=,
[a][b] [a]=[b]
Слайд 17Матрица бинарного отношения эквивалентности
Матрицу бинарного
отношения
эквивалентности
можно
представить
в
блочно-диагональном
виде, где каждая
подматрица,
состоящая из единиц,
соответствует классу
эквивалентности
Слайд 18Выводы. 1
При исследовании возникает задача выбора существенных свойств, деталей, признаков
моделируемого объекта. Отношение эквивалентности, с одной стороны, отождествляет второстепенные, несущественные
признаки и свойства, и, с другой – выделяет в качестве представителей классов эквивалентности основные свойства.Понятия "отношение эквивалентности", "фактор-множество", "классы эквивалентности" используются при построении математической модели некоторой реально функционирующей сложной системы.
Модель есть некоторое фактор-множество элементов моделируемого объекта относительно некоторого отношения эквивалентности, заданного на исходной системе.
Слайд 19Выводы. 2
Если моделируемый объект представлен в виде композиции элементов
некоторого базисного множества, то вопрос о соотношении модели и ее
прообраза разрешается на основе информации об элементах, на которых вводится отношение эквивалентности - либо это сами элементы базисного множества, либо некоторые подмножества элементов, либо подмножества множества подмножеств элементов.Слайд 20Тест-вопросы
1. Какое из отношений является
бинарным:
а) RM3; б) RM2; в)
R=M2.
2. Если матрица, описывающая бинарное
отношение, содержит на главной
диагонали
нули и единицы, то отношение:
а) рефлексивно; б) антирефлексивно;
в) не рефлексивно.
3. Если все вершины графа,
описывающего отношение, имеют петли,
то отношение:
а) рефлексивно; б) антирефлексивно;
в) не рефлексивно.
4. Если в графе, описывающем
отношение, имеется хотя бы одна
пара вершин, соединенных одной
дугой, является ли данное
отношение симметричным?
а) да; б) нет.
5. Классы эквивалентности:
а) попарно пересекаются;
б) попарно не пересекаются.
6. Верно ли, что любые два
элемента из одного класса
эквивалентности эквивалентны?
а) да; б) нет.