Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей и математическая статистика физический факультет 2018-2019
Содержание
- 1. Теория вероятностей и математическая статистика физический факультет 2018-2019
- 2. Теория вероятностей – математическая наука, Изучающая закономерности
- 3. Основные определенияПредмет изучения ТВ – модели случайных
- 4. Основные определенияСобытияДостоверное – происходит при каждом повторении
- 5. Вероятность событий
- 6. Вероятность событийКолода карт (52 карты) раздается на
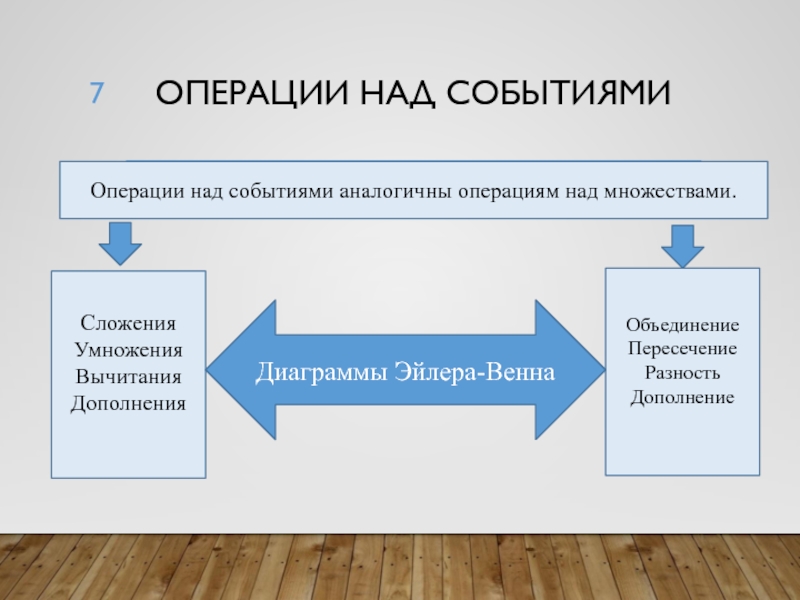
- 7. Операции над событиямиОперации над событиями аналогичны операциям над множествами. СложенияУмноженияВычитанияДополненияОбъединениеПересечениеРазность ДополнениеДиаграммы Эйлера-Венна
- 8. Условная вероятность. Независимые события
- 9. Формула умножения вероятностейΩР(А· В) = Р(А)· Р(В)Вероятность
- 10. Формула сложения вероятностей совместные и несовместные события
- 11. Противоположное событие
- 12. Формула полной вероятности Формула БайесаПусть нк
- 13. Скачать презентанцию
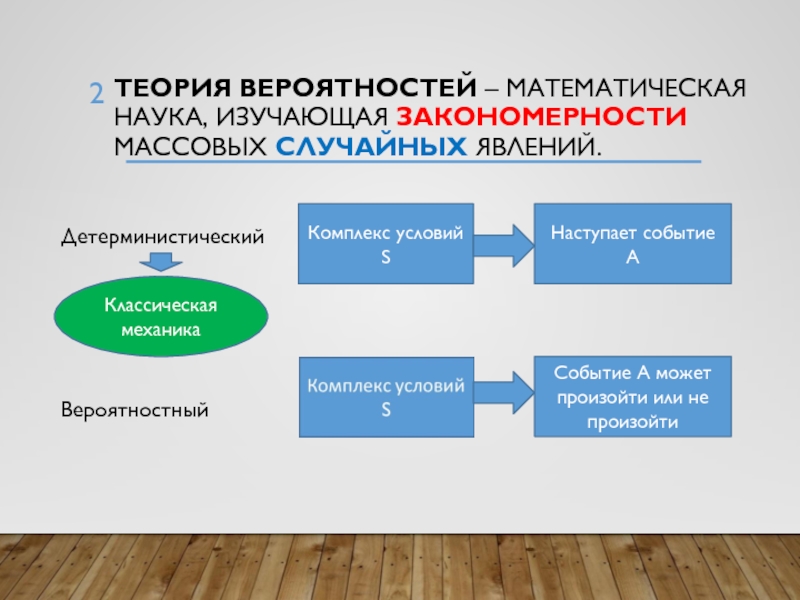
Теория вероятностей – математическая наука, Изучающая закономерности массовых случайных явлений. ДетерминистическийВероятностныйКомплекс условий SНаступает событие АСобытие А может произойти или не произойтиКлассическая механика
Слайды и текст этой презентации
Слайд 1Теория вероятностей
и
математическая статистика
физический факультет
2018-2019 уч.год
Тюрнева Т.Г., доцент
Кафедра теории
вероятностей и дискретной математики ИМЭИ ИГУ
Слайд 2Теория вероятностей – математическая наука, Изучающая закономерности массовых случайных явлений.
Детерминистический
Вероятностный
Комплекс условий S
Наступает событие А
Событие А может произойти или
не произойтиКлассическая механика
Слайд 3Основные определения
Предмет изучения ТВ – модели случайных экспериментов.
Случайный
эксперимент:
исход нельзя однозначно определить условиями проведения;
исходы обладают свойством статистической устойчивости;
эксперимент
м.б. проведен неограниченное количество раз при неизменном комплексе условий S.ОПР. Исход опыта – событие (или «исход эксперимента»).
ОПР. Множество простейших (неделимых) исходов эксперимента, таких что в каждом опыте происходит ровно один из них, называется пространством элементарных исходов (ПЭИ).
Мощность множества – конечная, счетная, континуум.
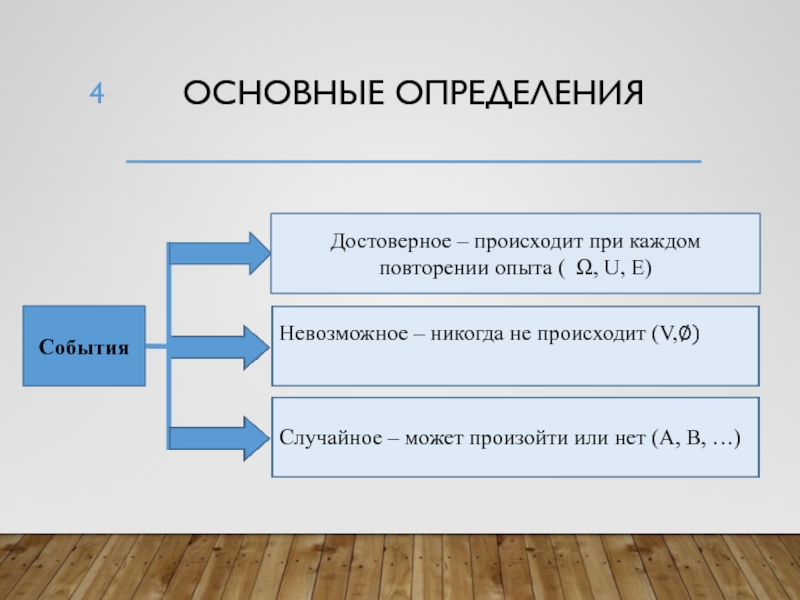
Слайд 4Основные определения
События
Достоверное – происходит при каждом повторении опыта ( Ω,
U, E)
Невозможное – никогда не происходит (V,∅)
Случайное – может произойти
или нет (А, В, …)
Слайд 6Вероятность событий
Колода карт (52 карты) раздается на четырех игроков. Найти
вероятность того, что данный игрок получит четыре туза.
Колода карт (52
карты) раздается на четырех игроков. Найти вероятность того, что данный игрок получит два короля, два туза и две дамы.
Слайд 7Операции над событиями
Операции над событиями аналогичны операциям над множествами.
Сложения
Умножения
Вычитания
Дополнения
Объединение
Пересечение
Разность
Дополнение
Диаграммы Эйлера-Венна
Слайд 9Формула умножения вероятностей
Ω
Р(А· В) = Р(А)· Р(В)
Вероятность совместного появления двух
зависимых событий равна произведению вероятности одного из них на условную
вероятность второго, вычисленную при условии, что первое событие произошло, т.е.Вероятность произведения независимых событий А и В вычисляется по формуле:
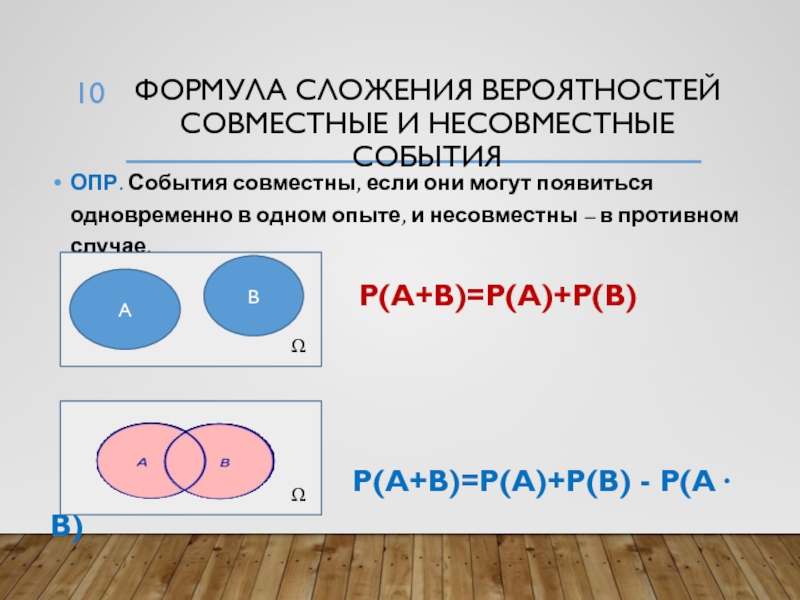
Слайд 10Формула сложения вероятностей
совместные и несовместные события
ОПР. События совместны, если они
могут появиться одновременно в одном опыте, и несовместны – в
противном случае.Р(А+В)=Р(А)+Р(В)
Р(А+В)=Р(А)+Р(В) - Р(А· В)
Ω
А
В
Ω
Слайд 12Формула полной вероятности
Формула Байеса
Пусть нк — полная группа событий.
Тогда вероятность любого события А может быть вычислена по
формуле:
