Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тұрақты электр тоғы 1
Содержание
- 1. Тұрақты электр тоғы 1
- 2. Дәріс жоспары
- 3. Электр зарядтарының бағытталған қозғалысын электр тогы деп
- 4. Күші мен бағыты уақытқа байланысты өзгермейтін тоқты тұрақты тоқ деп атайды.
- 5. Электрондық теория тұрғысынан алғанда тоқ күші әрбір
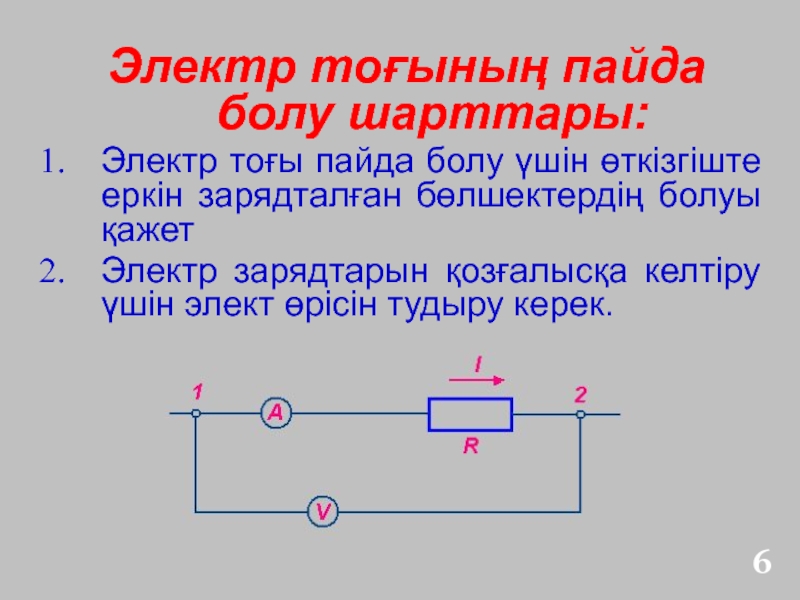
- 6. Электр тоғының пайда болу шарттары:Электр тоғы пайда
- 7. Электр тоғы тоқ тығыздығымен де сипатталады. Электр
- 8. Немiс физигi Георг Симон Ом Эрланг қаласында
- 9. Ол тiзбектiң бөлiгi үшiн ток күшiнiң кернеуге
- 10. Берілген өткізгіштің температурасы тұрақты болғанда сол өткізгіштің ұштарындағы кернеудің ондағы тоқ күшінің қатынасы тұрақты болады:
- 11. Бұл R-шамасы өткізгіштің өз бойынан өтіп жатқан
- 12. Өткізгіштің келергісіне кері шамаэлектрлік өткізгіш деп аталады.
- 13. Өткізгіштің меншікті электрлік кедергісі заттың тегіне, оның
- 14. - кедергінің температуралық коэффициенті. Т-термодинамикалық температура.
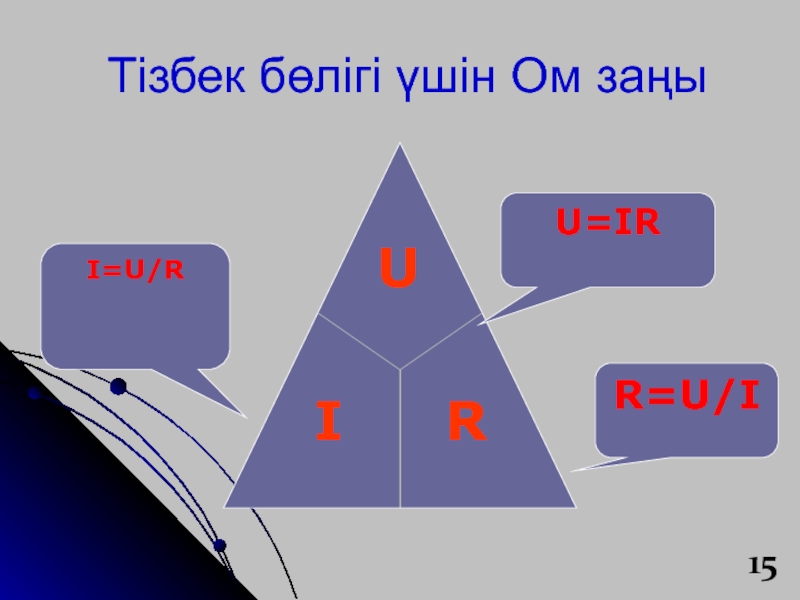
- 15. Тізбек бөлігі үшін Ом заңы I=U/RR=U/IU=IR
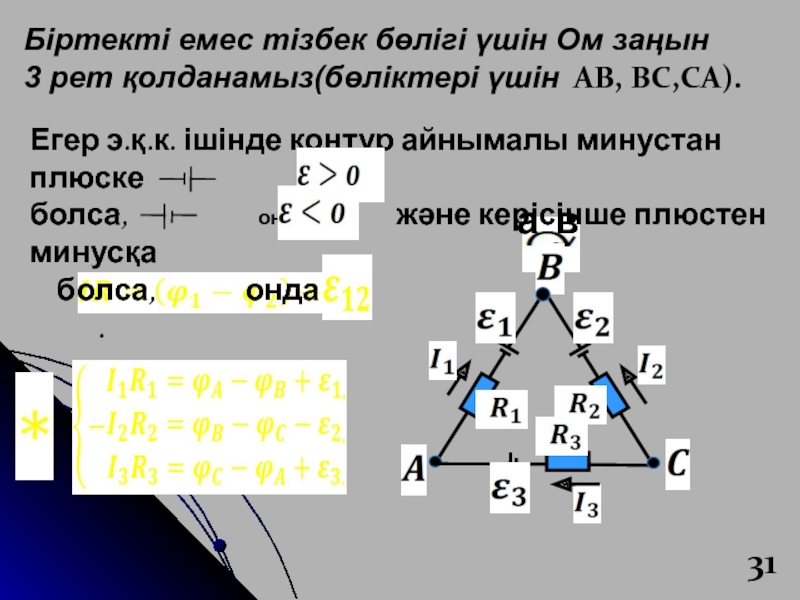
- 16. Біртекті емес тізбек бөлігіне арналған Ом заңы:
- 17. Ток көзі тарапынан өткізгіштегі зарядқа әсер етуші электрстатикалық емес күштерді бөгде күштер деп атайды.
- 18. Бөгде күштер электр зарядының өткізгіш бойымен орын
- 19. - өткізгіштің бойымен қозғалатын зарядтарға әсер ететін бөгде күш.
- 20. Тізбектің бөлігіндегі кернеу : Бірлік оң зарядты
- 21. Тоқтың жұмысы және қуаты. - тізбектің бөлігіндегі
- 22. Джоуль-Ленц заңы.
- 23. Тұйық тізбек үшін Ом заңы. - тоқ көзінің ішкі кедергісі, - сыртқы тізбектің кедергісі. - Э.Қ.Қ.
- 24. Дифференциал түрдегі Ом заңы.
- 25. Слайд 25
- 26. Слайд 26
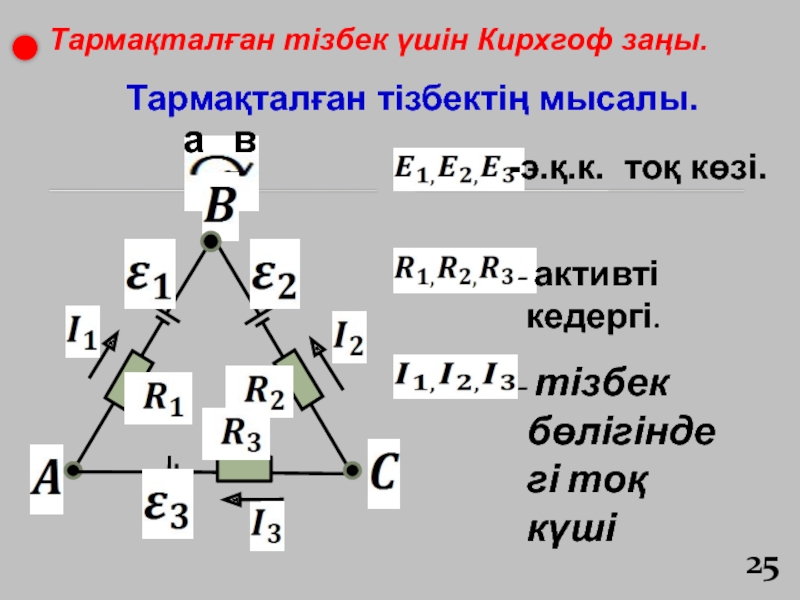
- 27. Түйін– тармақталған тізбектегі кез-келген нүкте, бұл
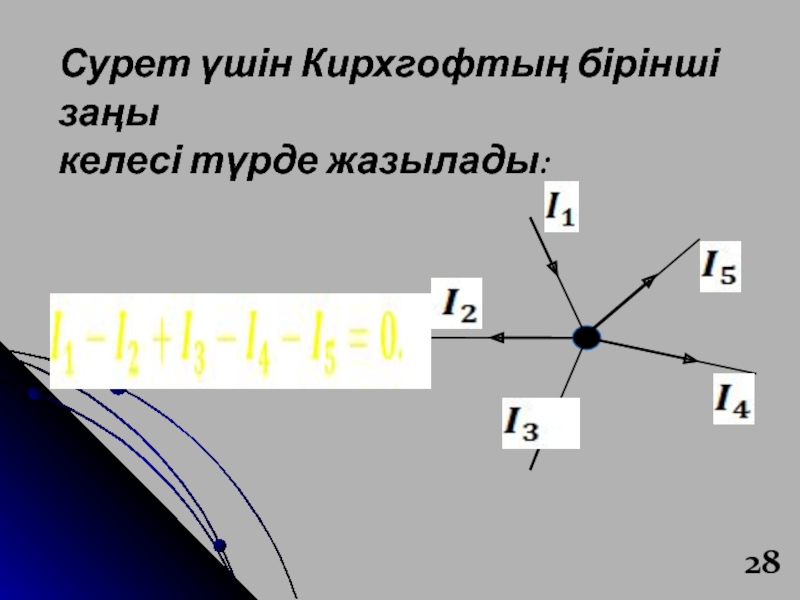
- 28. Сурет үшін Кирхгофтың бірінші заңы келесі түрде жазылады:
- 29. Кирхгофтың бірінші ережесі : электр зарядының сақталу
- 30. Кирхгофтың екінші ережесі: тармақталған тізбек үшін жалпы
- 31. Слайд 31
- 32. Слайд 32
- 33. Рекомендация 1.Барлық тізбек бөлігіндегі туынды ағытын таңдау;
- 34. Рекомендация 2.Контурды айналу бағытын таңдау және оны
- 35. Рекомендация 3. Саны ізделінетін мәндердің санына тең
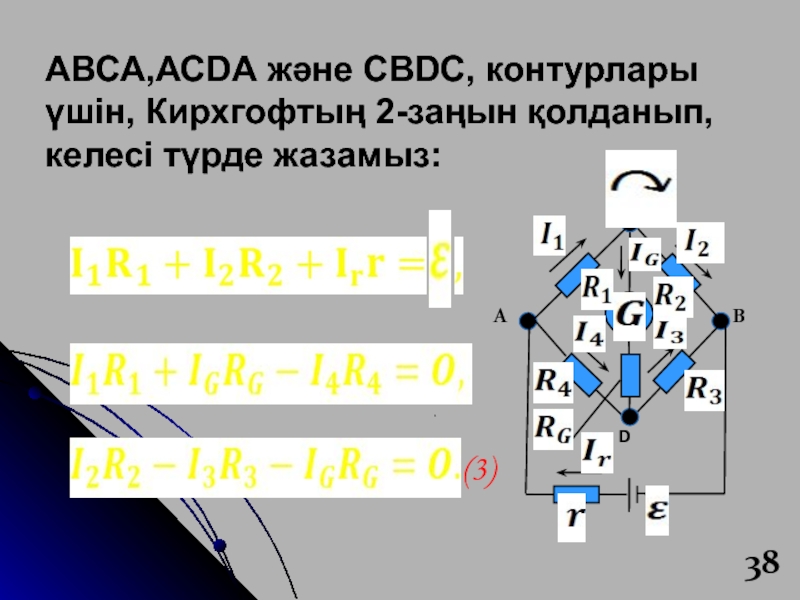
- 36. Уитсон көпірінің тізбегін есептеуге арналған Кирхгоф заңдарын
- 37. Слайд 37
- 38. Слайд 38
- 39. Егер барлық кекдергілер
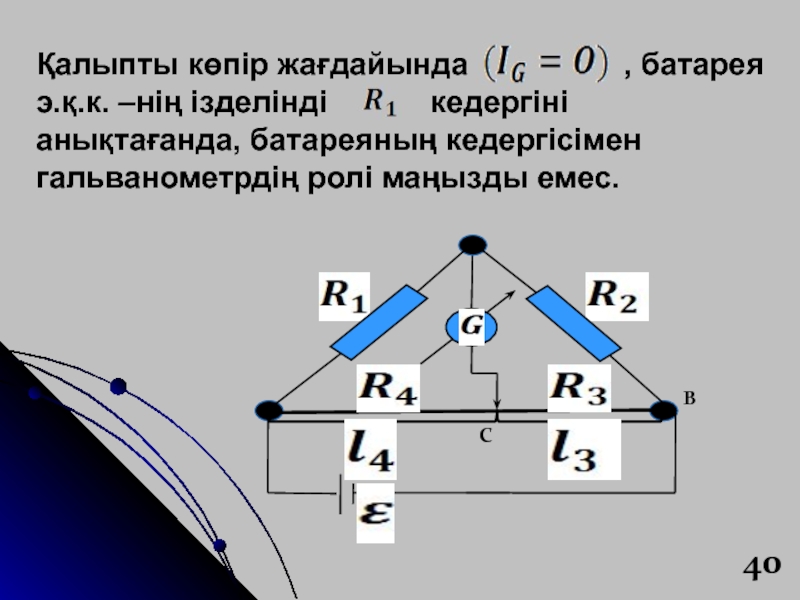
- 40. Қалыпты көпір жағдайында
- 41. Әдетте практикада Уитстонның реохордты көпірі қолданады. Онда
- 42. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Электр зарядтарының бағытталған қозғалысын электр тогы деп атайды.
Берілген көлемнен бірлік
уақыттың ішінде ағып өтетін электр мөлшерін тоқ күші деп атайды:
Слайд 5Электрондық теория тұрғысынан алғанда тоқ күші әрбір бөлшектің таситын зарядына,
бөлшектің концентрациясына, олардың бағытталған қозғалысының жылдамдығына және өткізгіштің көлденең қимасының
ауданына тәуелді.Слайд 6Электр тоғының пайда болу шарттары:
Электр тоғы пайда болу үшін өткізгіште
еркін зарядталған бөлшектердің болуы қажет
Электр зарядтарын қозғалысқа келтіру үшін элект
өрісін тудыру керек.Слайд 7Электр тоғы тоқ тығыздығымен де сипатталады. Электр тоғының тығыздығы j
деп өткізгіштің бір өлшем қимасынан өтетін тоқ күшін I
айтады.Тоқ тығыздығы - векторлық шама, оның бағыты тоқ бағытына, яғни оң зарядтардың қозғалысымен бағыттас болады.
Слайд 8Немiс физигi Георг Симон Ом Эрланг қаласында дүниеге келген. Георг
алғашында гимназияда, кейiннен Эрланг университетiнде оқиды да, Швейцарияда жеке мектепте
сабақ бере бастайды. 1811 ж. ол университеттегi емтихандарын тапсырып, философия докторы деген дәрежеге ие болады.1826 ж. өз заңын тұжырымдаған еңбегiн жарыққа шығарады. ЭҚК-i, кернеудiң азаюы, өткiзгiштiк деген ұғымдарды енгiзген Ом болатын.
Слайд 9Ол тiзбектiң бөлiгi үшiн ток күшiнiң кернеуге тәуелдiлiк заңын, сондай-ақ
тұйық тiзбектегi ток күшiн анықтайтын заңды ашты. Ом кедергiнiң өткiзгiш
ұзындығына және оның көлденең қимасының ауданына тәуелдiлiгiн тапты, ток күшiн өлшейтiн сезгiш приборды жасады. Ом кернеу көзi ретiнде термопараны пайдаланды (термопара – ұштары жалғанып дәнекерленген әр түрлi металдан жасалынған екi сым). Дәнекерленген ұштарының температуралар айырмасын арттыра отырып, кернеудi өзгерттi. Ол ток пен жылуөткiзгiштiк арасындағы ұқсастықты пайдаланып, электр тiзбегiнiң теориясын жасамақ болды.Бiрақ Омның ашқан жаңалықтары немiс ғалымдары арасында дұрыс қабылданбады. Өмiрiнiң соңғы жылдарында ғана оның еңбектерi таныла бастады. 1841 ж. Омға Лондон хандық қоғамының ең жоғары марапаты – Копли медалi берiлдi, ал 1850 ж. Мюнхен университетiнде кафедраны басқару ұсынылды.
Слайд 10Берілген өткізгіштің температурасы тұрақты болғанда сол өткізгіштің ұштарындағы кернеудің ондағы
тоқ күшінің қатынасы тұрақты болады:
Слайд 11Бұл R-шамасы өткізгіштің өз бойынан өтіп жатқан электрондардың қозғалысына кедергі,
яғни бөгет жасау қабілетін сипаттайтындықтан оны өткізгіштің кедергісі деп атайды.
Слайд 12Өткізгіштің келергісіне кері шама
электрлік өткізгіш деп аталады.
Өткізгіштің өлшем бірлігі
– сименс (См), 1см –кедергісі 1Ом тізбектің бөлігінің өткізгіштігі.
- Пропорционалдық коэффициент,заттың меншікті электрлік кедергісі.Слайд 13Өткізгіштің меншікті электрлік кедергісі заттың тегіне, оның температурасына тәуелді, яғни
меншікті кедергі соған сәйкес өткізгіш кедергісі мен температура арасындағы байланыс
сызықтық тәуелділік заңына бағынады.Слайд 17Ток көзі тарапынан өткізгіштегі зарядқа әсер етуші электрстатикалық емес күштерді
бөгде күштер деп атайды.
Слайд 18
Бөгде күштер электр зарядының өткізгіш бойымен орын ауыстыруы кезінде жұмыс
атқарады.
Бөгде күштердің оң бірлік зарядтың орнын ауыстыруы кезінде істелген жұмыс
мөлшерімен анықталатын физикалық шама электр қозғау күш (э.қ.к) деп аталады.
Э.Қ.К – тізбектің бөлігіндегі бөгде күштің энергетикарық сипаттамасы.
Электр қозғау күш (э.қ.к):
Слайд 20Тізбектің бөлігіндегі кернеу :
Бірлік оң зарядты орын ауыстыру барысында
кулон өрісі мен бөгде күштердің атқарған жұмысына тең
физикалық шама.Тізбектің бөлігі үшін кернеу потенциалдар айырмасына ғана тең.
Слайд 21Тоқтың жұмысы және қуаты.
- тізбектің бөлігіндегі
уақытта атқарылған электр тоғының жұмысы.
- электр тогының қуаты.
-
тұйық тізбектегі қуат.Слайд 23Тұйық тізбек үшін Ом заңы.
- тоқ көзінің ішкі кедергісі,
- сыртқы тізбектің кедергісі.
- Э.Қ.Қ.
Слайд 27 Түйін– тармақталған тізбектегі кез-келген нүкте, бұл нүкте кем дегенде
3 өткізгіш тоғы тұйықталады. Түйінге кіретін тоқ, оң тоқ күші,
ал түйінмен шығатын тоқ теріс болады.Слайд 29Кирхгофтың бірінші ережесі :
электр зарядының сақталу заңынан шығады. Қалыптасқан
тұрақты тоқ жағдайында өткізгіштің ешбір нүктесінде және бөлігінде электр зарядтары
жиналмауы тиіс.Кері жағдайда тоқтар тұрақты болып қала алмаушы еді.
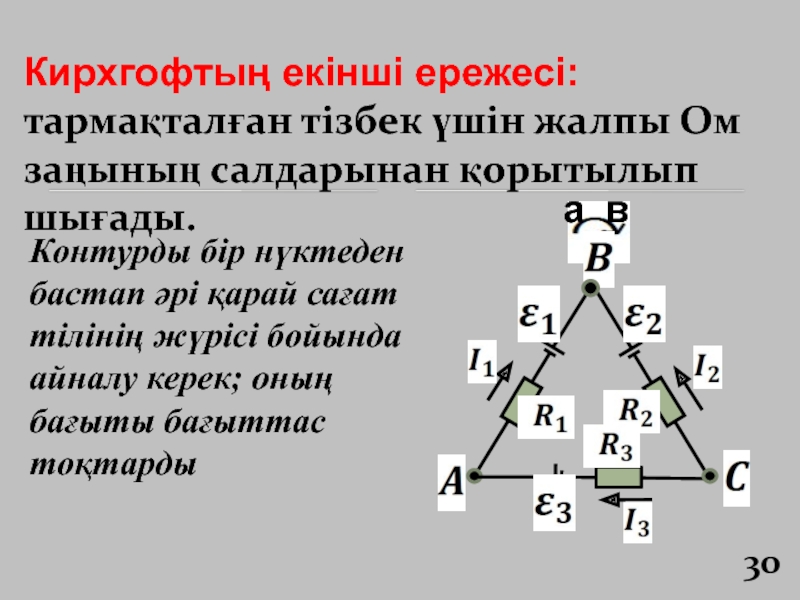
Слайд 30Кирхгофтың екінші ережесі: тармақталған тізбек үшін жалпы Ом заңының салдарынан
қорытылып шығады.
Контурды бір нүктеден бастап әрі қарай сағат тілінің жүрісі
бойында айналу керек; оның бағыты бағыттас тоқтардыСлайд 33Рекомендация 1.
Барлық тізбек бөлігіндегі туынды ағытын таңдау; реалдық тоқтың бағыты
есепті шешу кезінде анықталады: егер, ізделінетін ток оң болса, онда
оныңбағыты дұрыс алынған, ал егер теріс болса – оның бастапқы бағыты таңдаған бағытқа қарама-қарсы болады.Слайд 34Рекомендация 2.
Контурды айналу бағытын таңдау және оны қатаң ұстану. IR
туындысы оң болады, егер осы бөлігінде айналу бағытымен сәйкес келсе,
және керісінше, таңдап алынған айналу бағытымен қозғалатын э.қ.к. оң, кері қозғалса – теріс болады.Слайд 35Рекомендация 3.
Саны ізделінетін мәндердің санына тең болатындай теңдеулер жүйесін
құру (теңдеулер жүйесіне тізбектің кедергілер мен э.қ.к. кіру керек); әрбір
қарастырылып отырған контурға алдыңғы контурда болмаған ең болмағанда бір элемент кіру керек, әйтпесе құрылған теңдеулердің жай комбинациясы болатын теңдеу шығады.Слайд 36Уитсон көпірінің тізбегін есептеуге
арналған Кирхгоф заңдарын қолдауға
мысал:
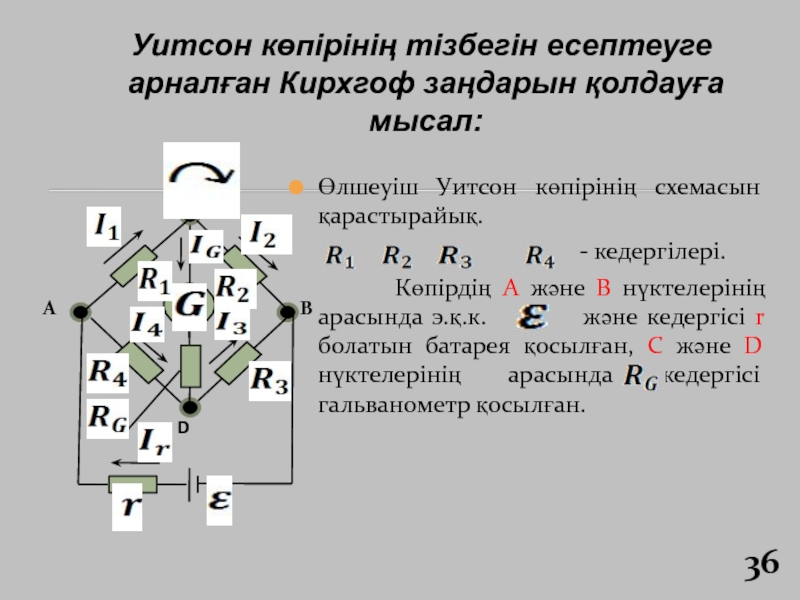
Өлшеуіш Уитсон
көпірінің схемасын қарастырайық.
- кедергілері.Көпірдің А және В нүктелерінің арасында э.қ.к. және кедергісі r болатын батарея қосылған, С және D нүктелерінің арасында кедергісі гальванометр қосылған.
Слайд 39 Егер барлық кекдергілер мен э.қ.к. Белгілі
болса, онда алынған алты теңдеуді шеше отырып, белгілі тоқтарды табуға
болады.кедергілерді өзгерте отырып, гальванометрден өтетін тоқтың мәні нольге тең болатындай жасауға болады
Онда (2)-ден табамыз,
ал, (3)-тен табамыз,
(4) және (5) –тен шығады,
немесе
Слайд 40Қалыпты көпір жағдайында
, батарея э.қ.к. –нің ізделінді
кедергіні анықтағанда, батареяның кедергісімен гальванометрдің ролі маңызды емес.Слайд 41Әдетте практикада Уитстонның реохордты көпірі қолданады. Онда және
кедергілері өз алдына кедергісі үлкен ұзын біртекті сым
болады,қатынасын қатынасымен ауыстыруға болады.
(6)-ны қоланып, жазуға болады:
және ұзындықтарын шкала бойынша өлшеуге болады, ал белгілі. Сондықтан (7) теңдеу белгілі
кедергіні табу үшін қолданылады.