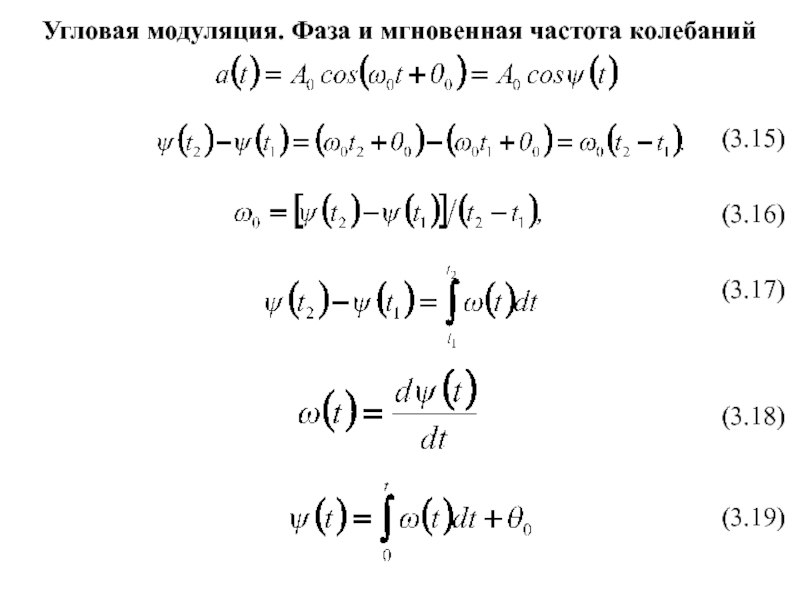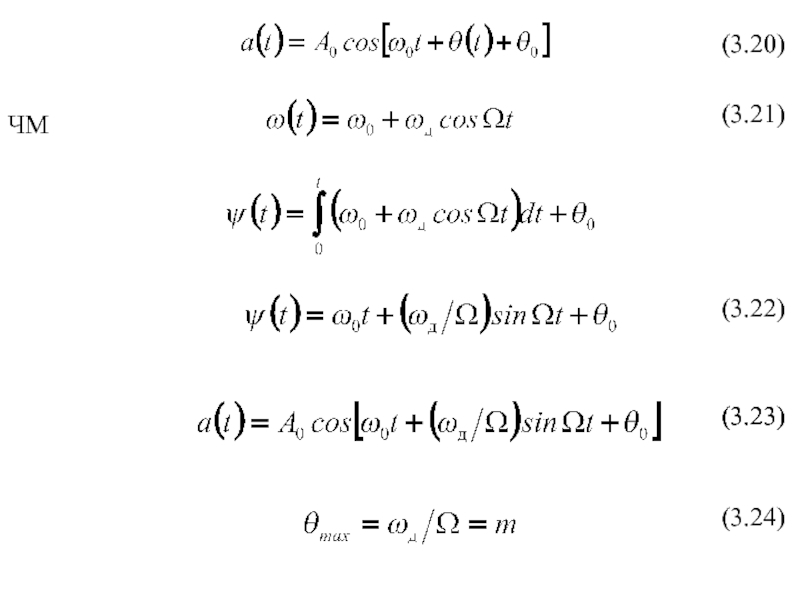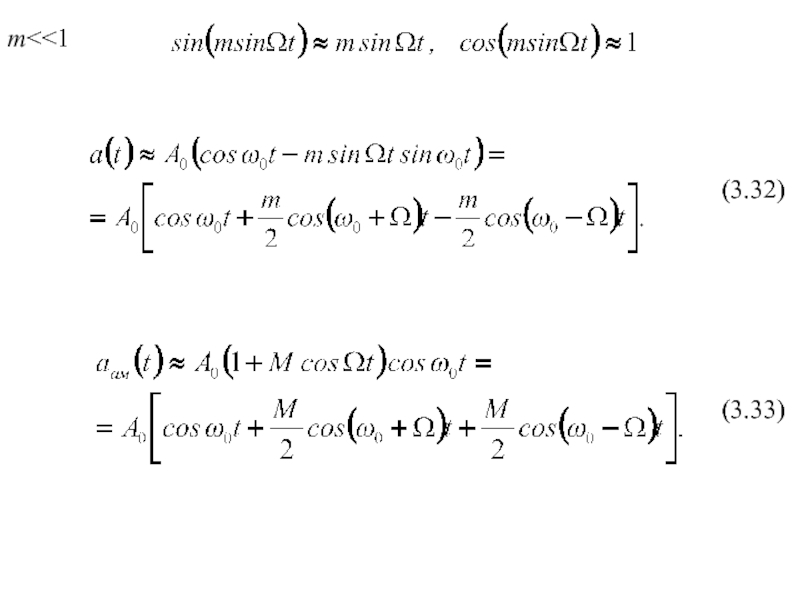TheSlide.ru

Угловая модуляция

Содержание

1. Угловая модуляция
2. (3.20) (3.22) (3.21) (3.23) (3.24) ЧМ(3.23)
3. θ(t)=θmaxsinΩt ФМ(3.23`) (3.21`) θmaxΩ=ωд, т. е.
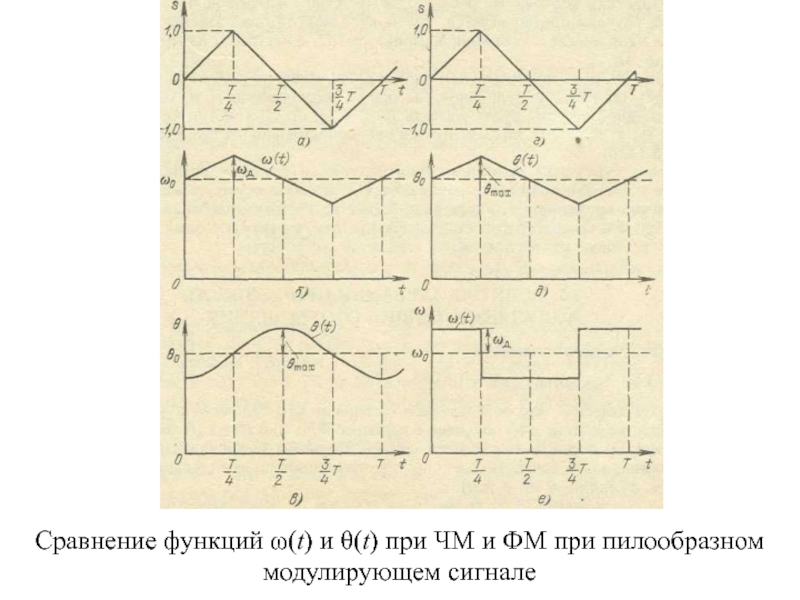
4. Сравнение функций ω(t) и θ(t) при ЧМ и ФМ при пилообразноммодулирующем сигнале
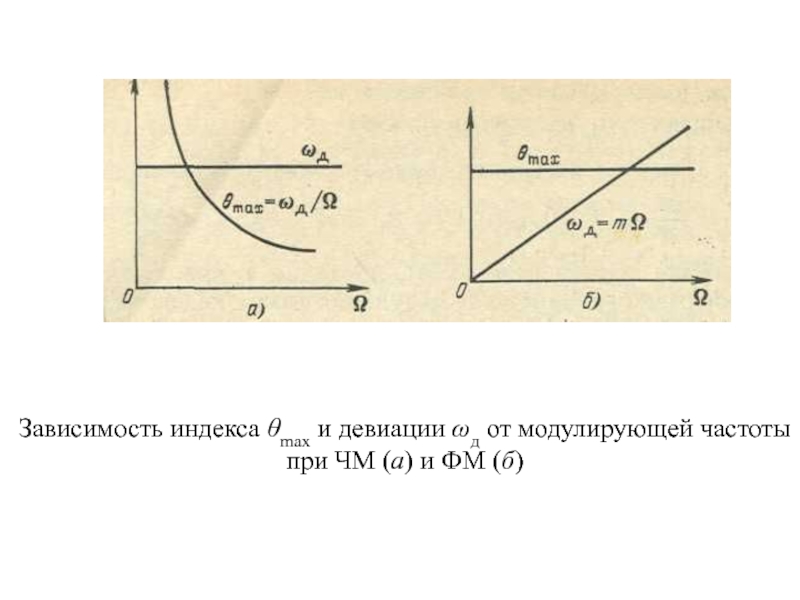
5. Зависимость индекса θmax и девиации ωд от модулирующей частотыпри ЧМ (а) и ФМ (б)
6. Спектр колебания при угловой модуляции. Общие соотношения(3.25)(3.26)Модулированное
7. Спектр колебания при гармонической угловой модуляции(3.25`) (3.27)
8. m
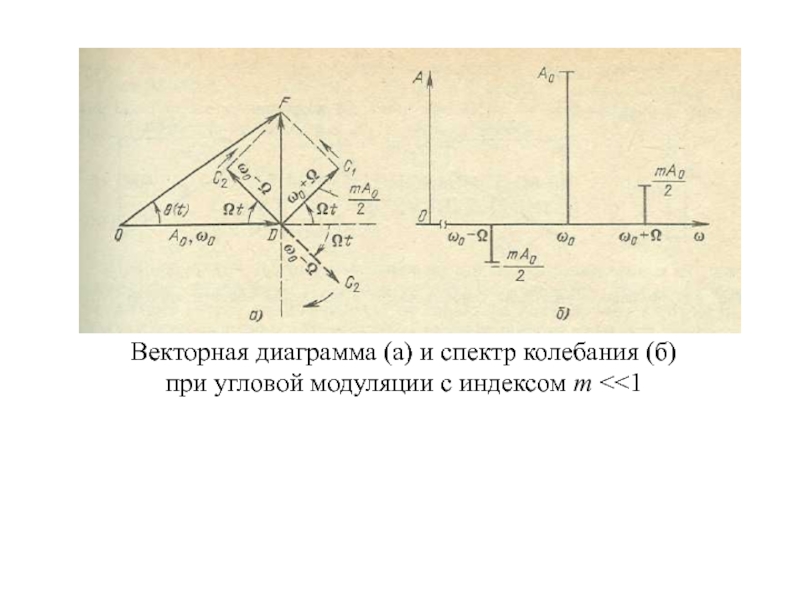
9. Векторная диаграмма (а) и спектр колебания (б) при угловой модуляции с индексом m
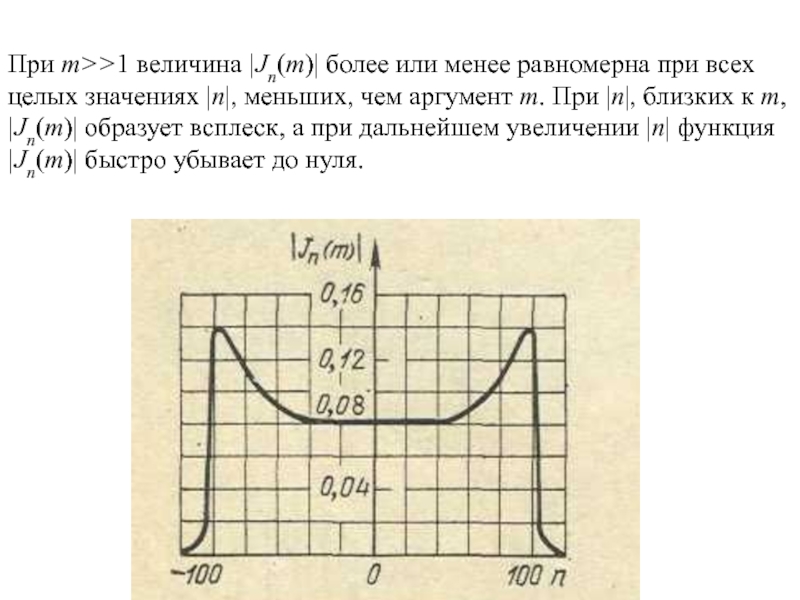
10. При m>>1 величина |Jn(m)| более или менее
11. Приравнивая это максимальное значение nmах величине m,
12. Ширина спектра ЧМ колебания при больших значениях индекса модуляции2|nmax|Ω≈2 ωд. (3.34)
13. Скачать презентанцию

(3.20) (3.22) (3.21) (3.23) (3.24) ЧМ(3.23)

Слайды и текст этой презентации

Слайд 1Угловая модуляция. Фаза и мгновенная частота колебаний

(3.15)
(3.16)
(3.17)
(3.18)

(3.19)

Угловая модуляция. Фаза и мгновенная частота колебаний(3.15) (3.16) (3.17) (3.18) (3.19)

Слайд 2
(3.20)

(3.22)

(3.21)

(3.23)

(3.24)
ЧМ
(3.23)

(3.20) (3.22) (3.21) (3.23) (3.24) ЧМ(3.23)

Слайд 3θ(t)=θmaxsinΩt
ФМ

(3.23`)

(3.21`)

θmaxΩ=ωд, т. е. гармоническая модуляция

фазы с индексом θmax
эквивалентна частотной модуляции с девиацией ωд=θmaxΩ.
θ=θmaxsinΩt

при ФМ

θ=(ωд/Ω)sinΩt при ЧМ
(когда Δω=ωдcosΩt)

θ(t)=θmaxsinΩt ФМ(3.23`) (3.21`) θmaxΩ=ωд, т. е. гармоническая модуляция фазы с индексом θmax эквивалентна частотной модуляции с

Слайд 4Сравнение функций ω(t) и θ(t) при ЧМ и ФМ при

пилообразном
модулирующем сигнале

Сравнение функций ω(t) и θ(t) при ЧМ и ФМ при пилообразноммодулирующем сигнале

Слайд 5Зависимость индекса θmax и девиации ωд от модулирующей частоты
при ЧМ

(а) и ФМ (б)

Зависимость индекса θmax и девиации ωд от модулирующей частотыпри ЧМ (а) и ФМ (б)

Слайд 6Спектр колебания при угловой модуляции. Общие соотношения

(3.25)

(3.26)
Модулированное по углу колебание

можно рассматривать как сумму
двух квадратурных колебаний: косинусного ас(t)=А0cosθ(t)cosω0t и
синусного аs(t)=А0sinθ(t)sinω0t,

каждое из которых модулировано
только по амплитуде;
закон AM для косинусного колебания определяется медленной
функцией cosθ(t), а синусного – функцией sinθ(t).

Спектр колебания при угловой модуляции. Общие соотношения(3.25)(3.26)Модулированное по углу колебание можно рассматривать как суммудвух квадратурных колебаний: косинусного

Слайд 7Спектр колебания при гармонической угловой модуляции

(3.25`)

(3.27)

Спектр колебания при гармонической угловой модуляции(3.25`) (3.27)

Слайд 8m

Слайд 9Векторная диаграмма (а) и спектр колебания (б)
при угловой модуляции

с индексом m

Векторная диаграмма (а) и спектр колебания (б) при угловой модуляции с индексом m

Слайд 10При m>>1 величина |Jn(m)| более или менее равномерна при всех

целых значениях |n|, меньших, чем аргумент m. При |n|, близких

к m, |Jn(m)| образует всплеск, а при дальнейшем увеличении |n| функция |Jn(m)| быстро убывает до нуля.

При m>>1 величина |Jn(m)| более или менее равномерна при всех целых значениях |n|, меньших, чем аргумент m.

Слайд 11Приравнивая это максимальное значение nmах величине m, приходим к выводу,

что полная ширина спектра частотно-модулированного колебания
2|nmax|Ω≈2mΩ.
Но m=ωд/Ω, следовательно, при больших

индексах модуляции ширина спектра модулированного колебания близка к удвоенной девиации частоты
2|nmax|Ω≈2ωд. (3.34)

Наивысший номер n боковой частоты, которую еще необходимо принимать в расчет, приблизительно равен индексу модуляции m (в данном случае n=100).

Приравнивая это максимальное значение nmах величине m, приходим к выводу, что полная ширина спектра частотно-модулированного колебания2|nmax|Ω≈2mΩ.Но m=ωд/Ω,

Слайд 12Ширина спектра ЧМ колебания при больших значениях
индекса модуляции
2|nmax|Ω≈2 ωд.

(3.34)

Ширина спектра ЧМ колебания при больших значениях индекса модуляции2|nmax|Ω≈2 ωд. (3.34)

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей