Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уральский государственный технический университет - УПИ Кафедра “ Инженерная
Содержание
- 1. Уральский государственный технический университет - УПИ Кафедра “ Инженерная
- 2. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ занимается построением изображений и изучениемпространственных объектов по их изображениям графическими методами
- 3. А1 - горизонтальная проекция точки А;
- 4. ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ - ЭПЮРОртогональный чертеж или эпюр
- 5. ВИДЫ ПРЯМЫХ ЛИНИЙПрямые частного положения Прямые общего положенияОртогональный чертеж прямой линии
- 6. Прямые частного положения: • ПРОЕЦИРУЮЩИЕ
- 7. 1. Проецирующие прямые ZXYА1 Ξ B1B2А2ОAB ┴
- 8. 2. Прямые уровня Горизонтальная прямая, горизонталь hXZYА2А1В2В1AВ
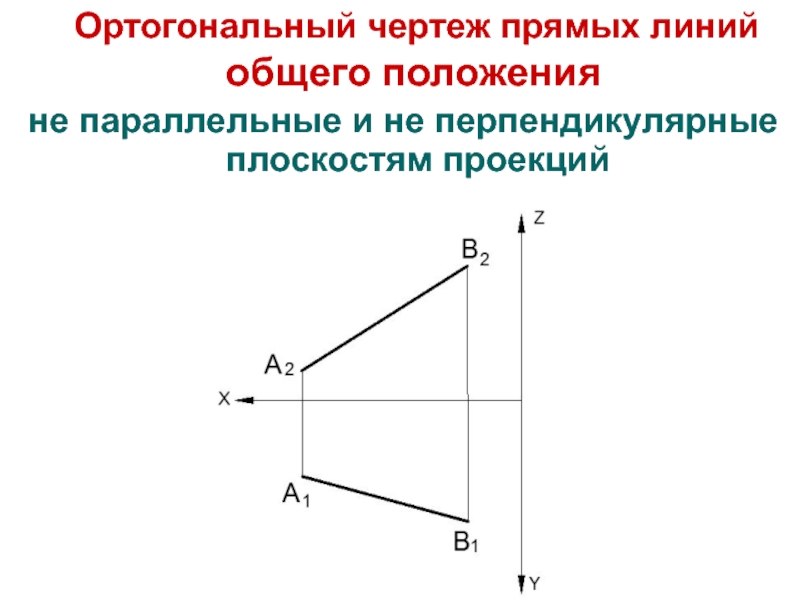
- 9. Ортогональный чертеж прямых линий общего положенияне параллельные и не перпендикулярные плоскостям проекций
- 10. ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ ПЛОСКОСТИПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ
- 11. YZXaп1aП3aП2axayazaa-плоскость;aп1 - горизонтальный след плоскости a;
- 12. ПЛОСКОСТИ УРОВНЯ плоскости параллельные плоскостям проекций –
- 13. Горизонтальная плоскость уровня aII П1ZXYYaП2aП3azYZXaП3aП2azaА1В1С1А2В2С2А1С1В1А2В2С2ΔАВС; IABCI=IA1B1C1I
- 14. ZXYYbп1bП3byYZXbп1bП3bybyФронтальная плоскость уровня b I| П2А1В1С1С2В2А2bΔАВС; IABCI=IA2B2C2I
- 15. 2. Проецирующие плоскостиГоризонтально проецирующая плоскость ┴П1XYY П2 П3ZX п1П2 xxZ п1 П3Y yy y yА1В1С1А2В2С2ΔАВС
- 16. Фронтально проецирующая плоскость ┴ П2ZXYYП2п1xYZXП2zП3П1П3zxА2В2С2А1В1С1fΔАВС
- 17. ПОВЕРХНОСТИ
- 18. ПОВЕРХНОСТИПОВЕРХНОСТЬМНОЖЕСТВО ПОЛОЖЕНИЙ ЛИНИИ ПЕРЕМЕЩАЮЩЕЙСЯ В ПРОСТРАНСТВЕ ПО
- 19. НаправляющаяОбразующая
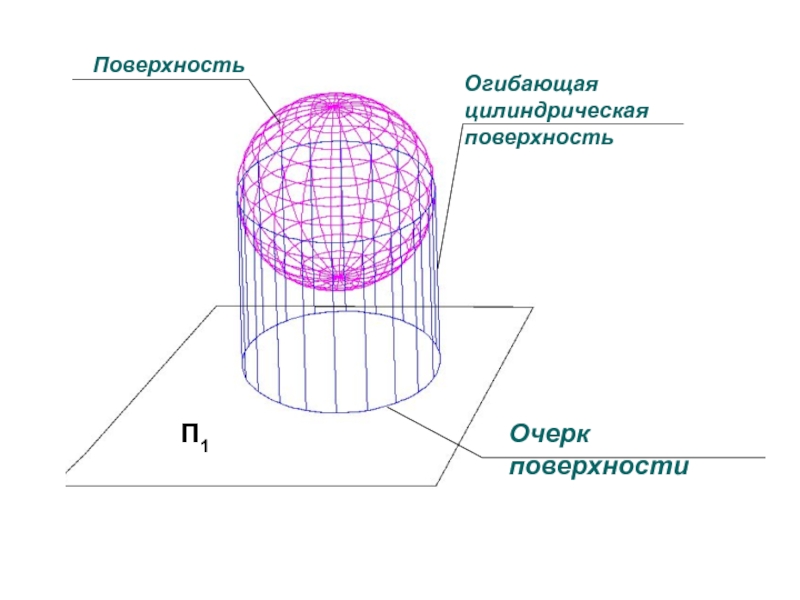
- 20. ОЧЕРК ПОВЕРХНОСТИОчерк поверхности при ортогональном проецировании –
- 21. П1Очерк поверхностиОгибающая цилиндрическая поверхностьПоверхность
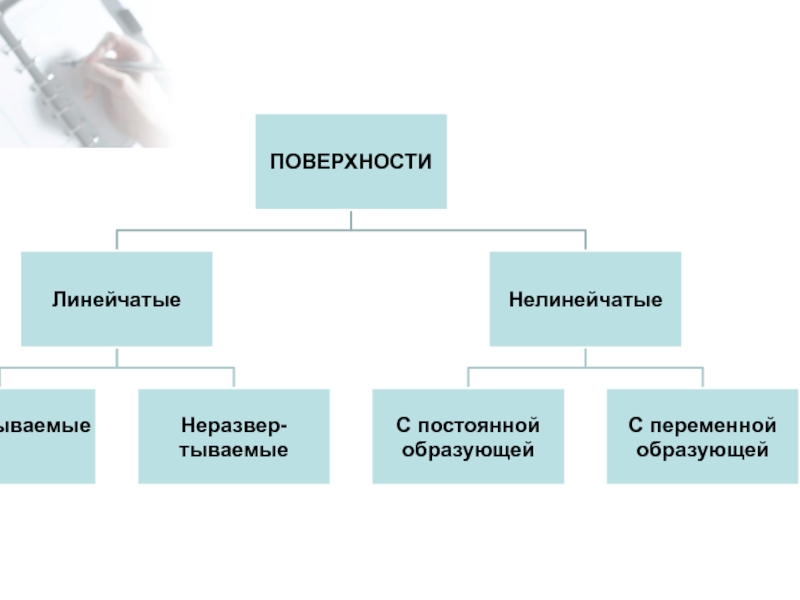
- 22. КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
- 23. Слайд 23
- 24. Гранные поверхностиПризма - образуется при движении прямолинейной
- 25. Пирамида – образуется при движении прямолинейной образующей
- 26. ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯL2i2i1L1 m – криволинейная
- 27. ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ i – ось вращения L – прямолинейная образующая S – вершина конической поверхностиL2L1i2i1S
- 28. ПОВЕРХНОСТЬ CФЕРЫI – ось вращенияn – криволинейная
- 29. ТОРОВАЯ ПОВЕРХНОСТЬ ОТКРЫТЫЙ ТОРi – ось
- 30. ТОРОВАЯ ПОВЕРХНОСТЬ САМОПЕРЕСЕКАЮЩИЙСЯ ТОР (тор -
- 31. СЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ- это линия пересечения поверхности и плоскостиили совокупность точек одновременно принадлежащих поверхности и плоскости
- 32. СЕЧЕНИЕ ГРАННОЙ ПОВЕРХНОСТИСечение гранной поверхности – многоугольник,
- 33. СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ1. αbi – окружность2. β^ i – эллипс3. γ ll i - прямоугольникL2i2i1L1αп2βп2γ п111211222
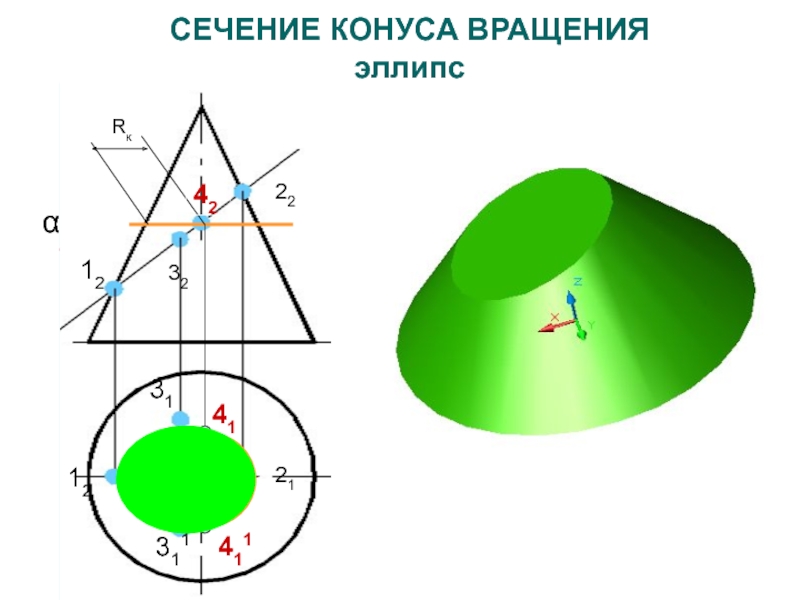
- 34. СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ1. α bi – окружность2.
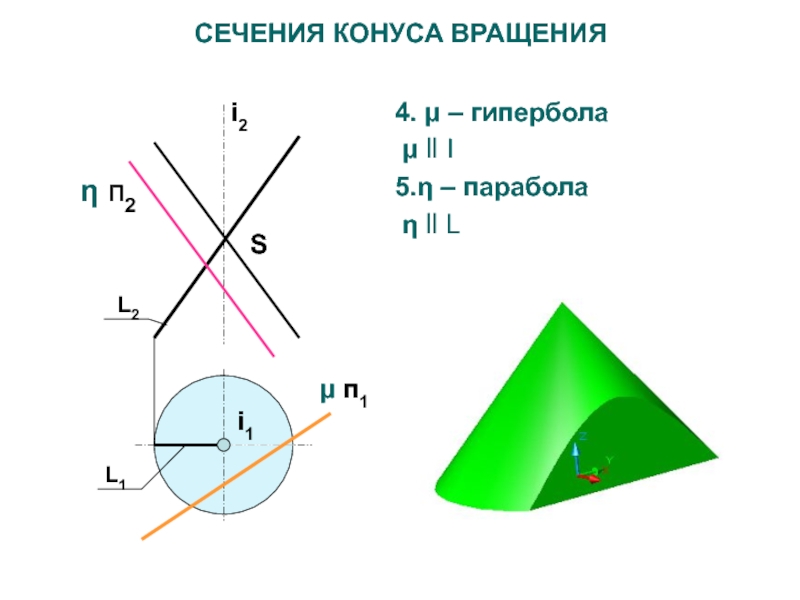
- 35. 4. μ – гипербола μ ll I5.η – парабола η ll LL2L1i2i1SСЕЧЕНИЯ КОНУСА ВРАЩЕНИЯμ п1η п2
- 36. СЕЧЕНИЯ СФЕРЫ Сечение сферы плоскостью –
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
- 48. Линия пересечения поверхностей - совокупность точек
- 49. Линия пересечения многогранника и поверхности вращения -
- 50. Алгоритм решения задач1. Анализ заданных поверхностей-
- 51. 2. Определить характерные точки линии пересеченияточки пересечения
- 52. Способ вспомогательных секущих плоскостей1. Провести вспомогательную секущую
- 53. 4. Соединить линией, полученные точки
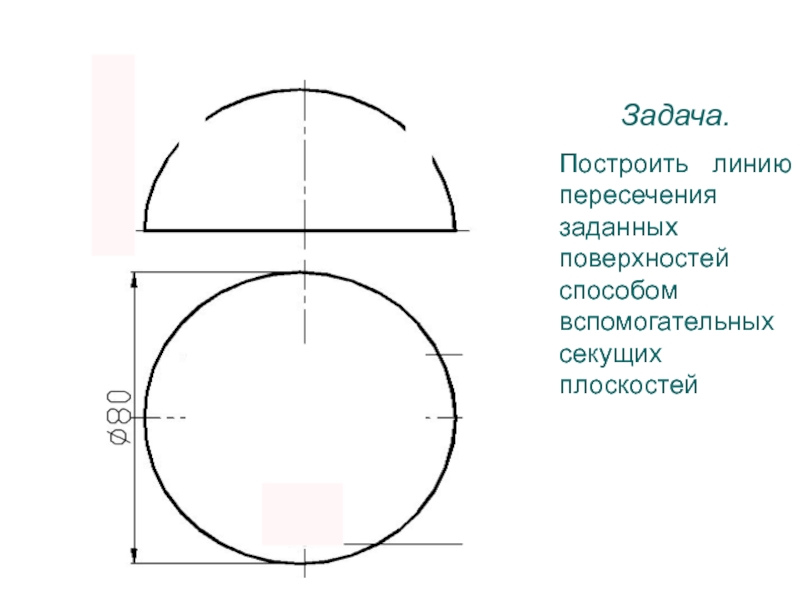
- 54. Задача. Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей
- 55. Слайд 55
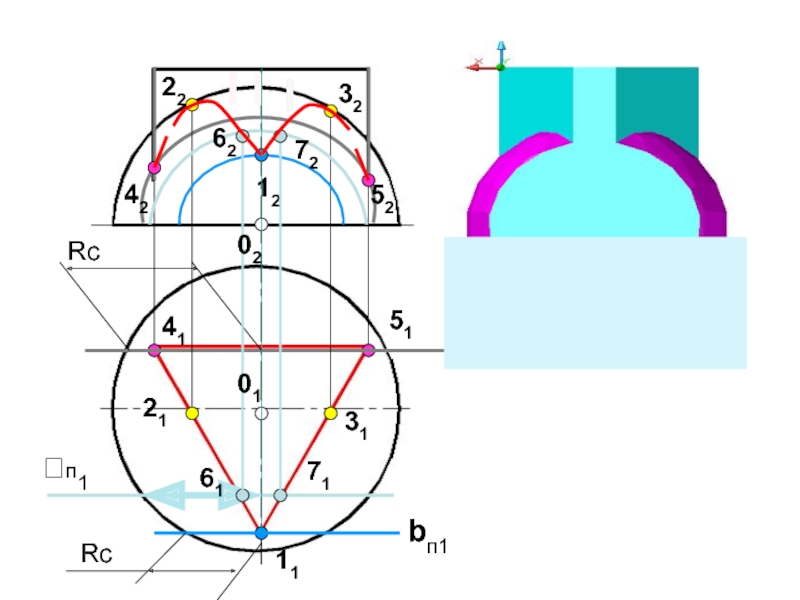
- 56. п1Rc4152425132223121bп1Rc1112п1716172620102
- 57. Слайд 57
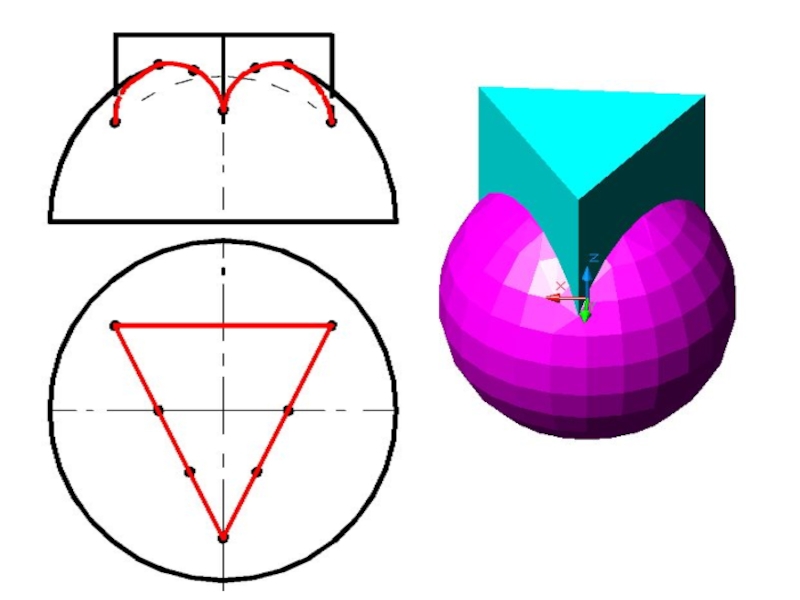
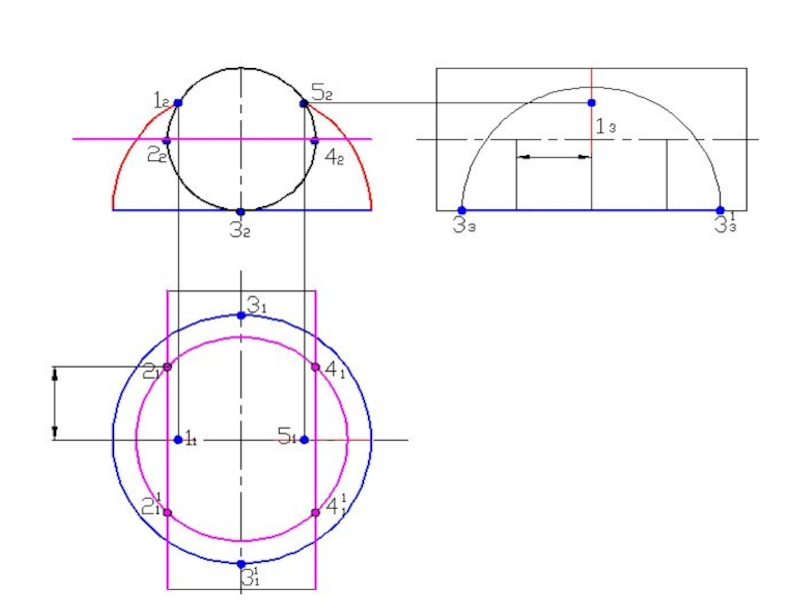
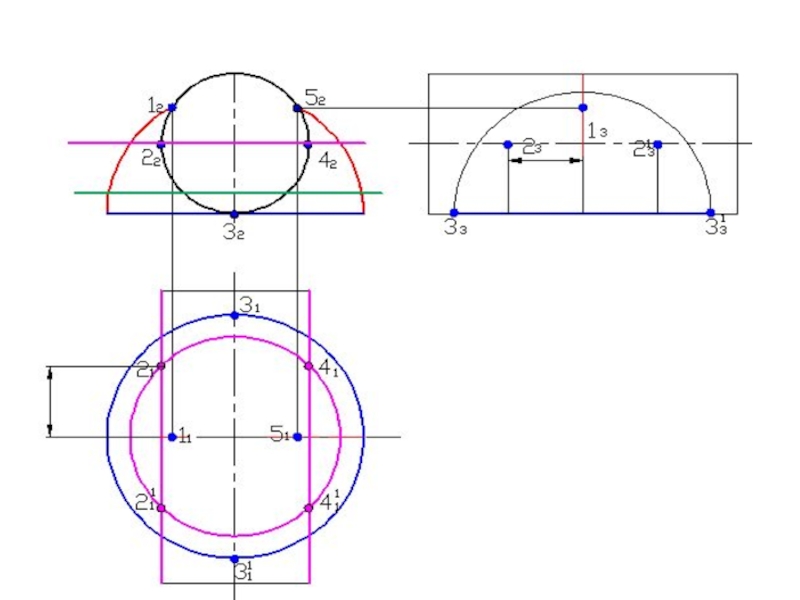
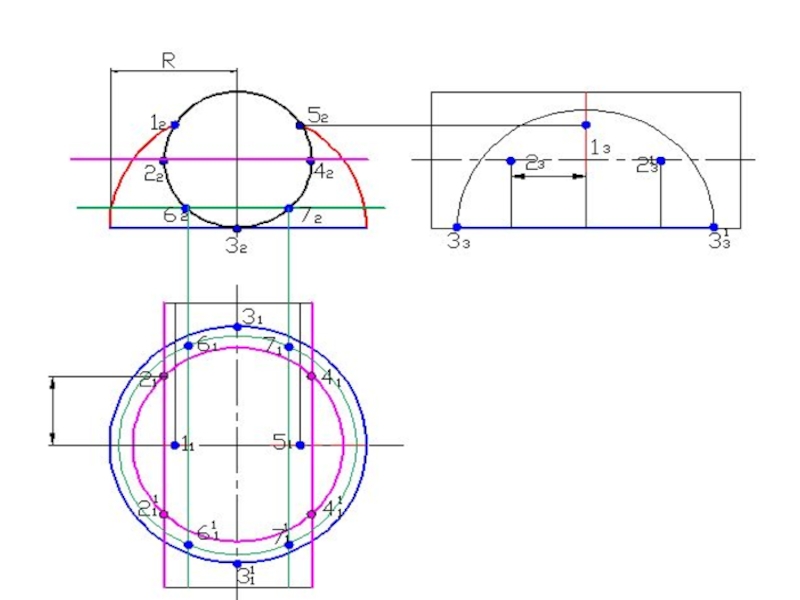
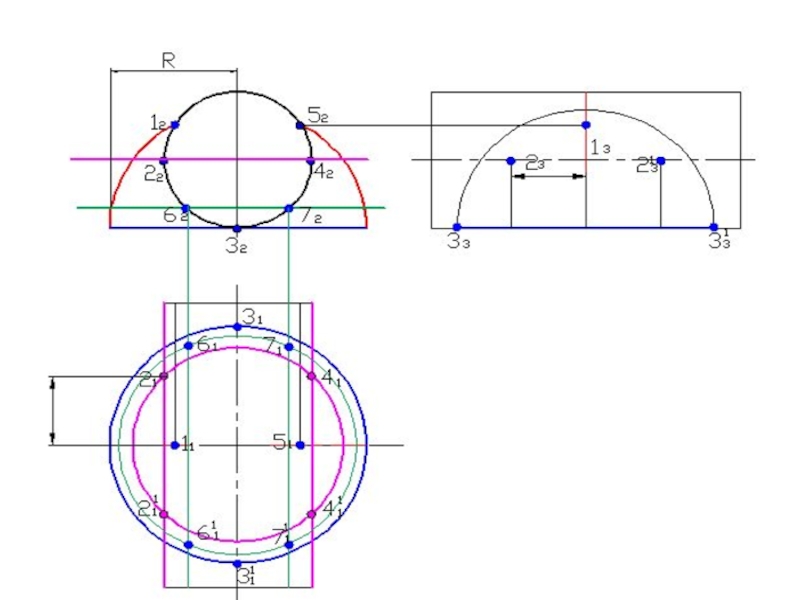
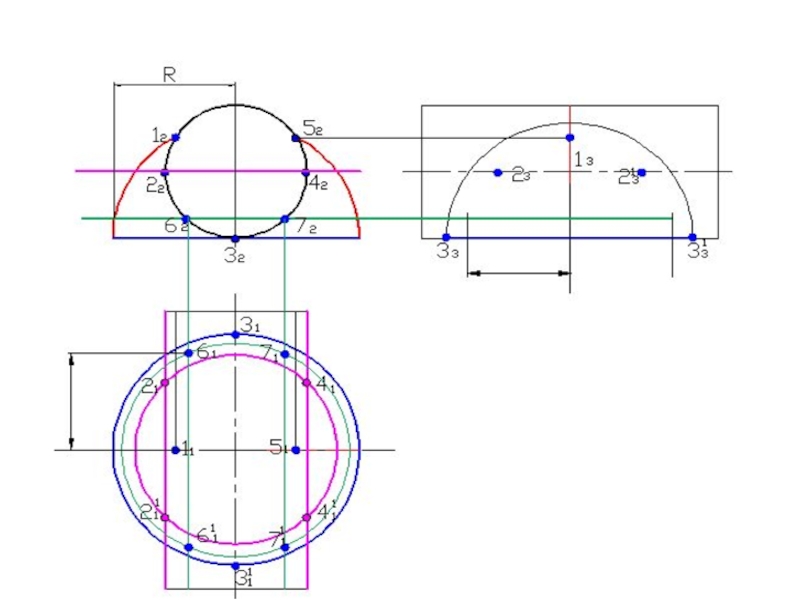
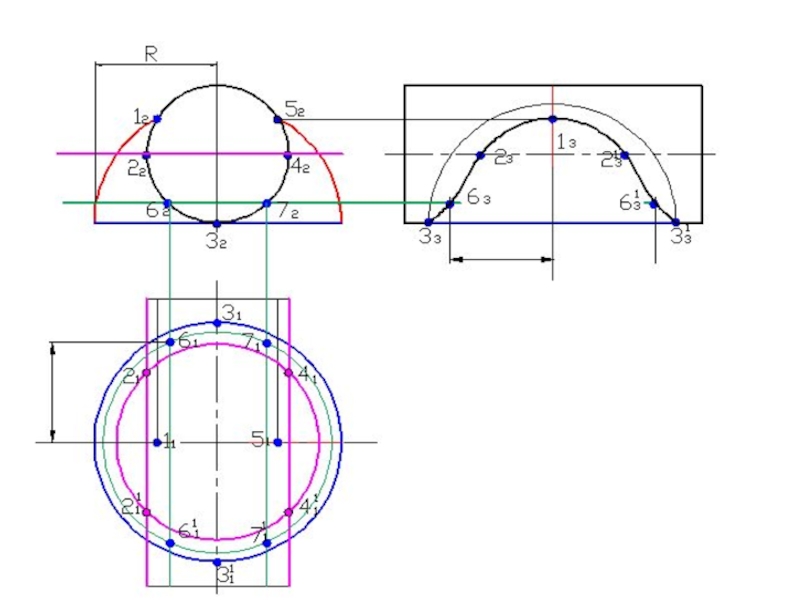
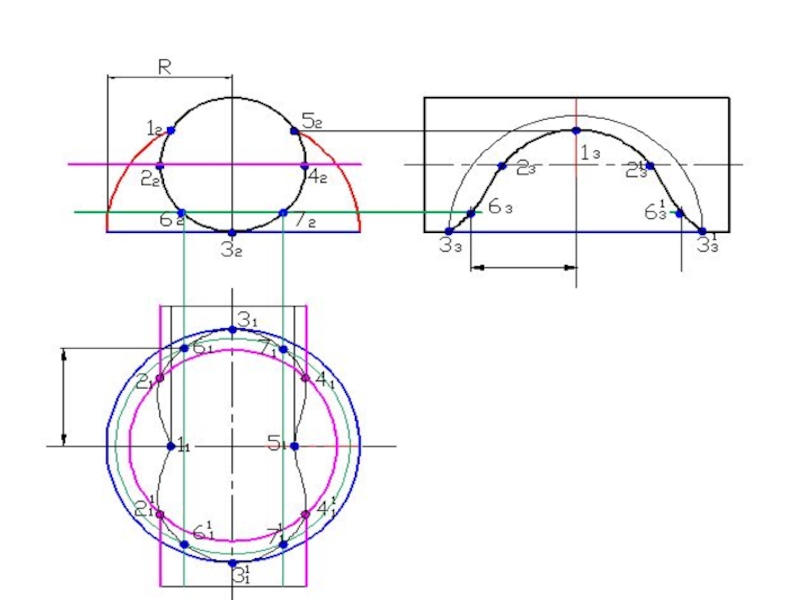
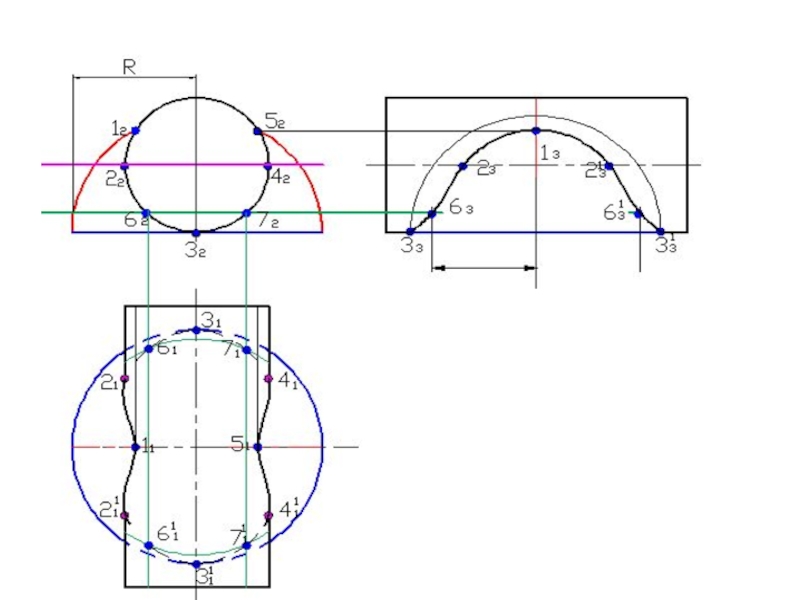
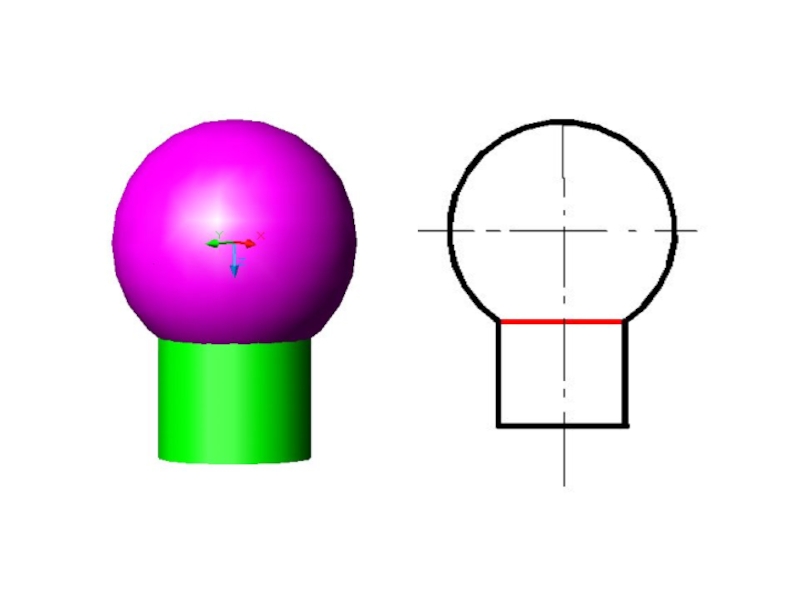
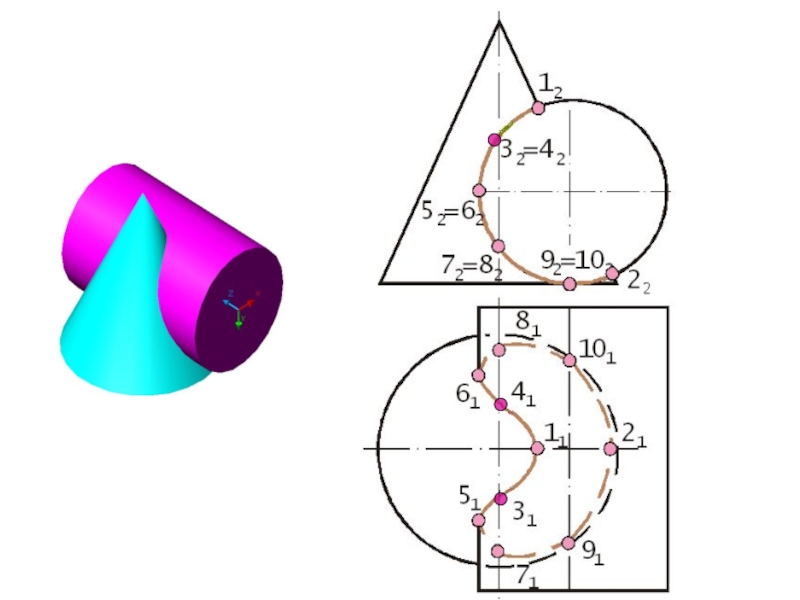
- 58. Построить линию пересечения поверхностейПолусфера диаметром 90 ммЦилиндр диаметром 50 мм
- 59. Слайд 59
- 60. Слайд 60
- 61. Слайд 61
- 62. Слайд 62
- 63. Слайд 63
- 64. Слайд 64
- 65. Слайд 65
- 66. Слайд 66
- 67. Слайд 67
- 68. Слайд 68
- 69. Слайд 69
- 70. Слайд 70
- 71. Слайд 71
- 72. СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ КОНЦЕНТРИЧЕСКИХ СФЕР
- 73. ОСНОВНОЙ ПРИНЦИП СФЕРА С ПОВЕРХНОСТЯМИ
- 74. Слайд 74
- 75. СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР1. ПЕРЕСЕКАЮТСЯ ПОВЕРХНОСТИ ВРАЩЕНИЯ
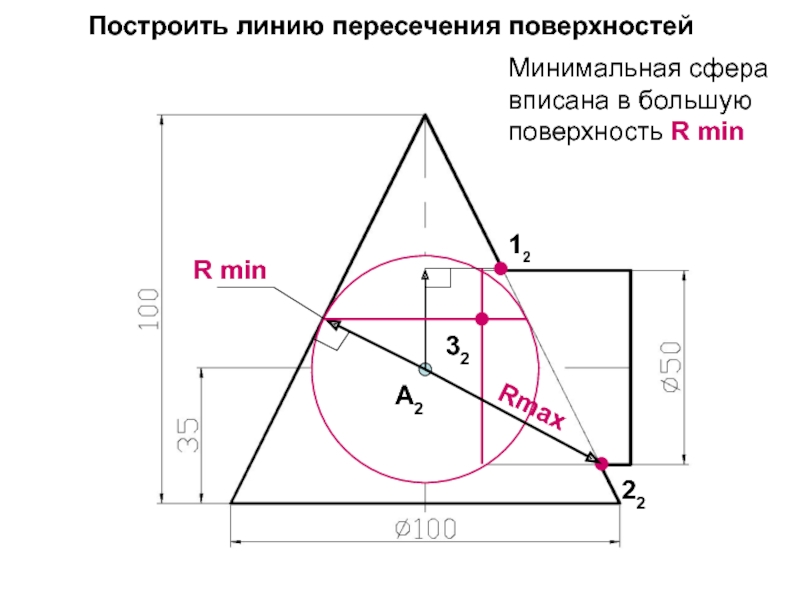
- 76. Построить линию пересечения поверхностейА2Минимальная сфера вписана в большую поверхность R minR min321222Rmax
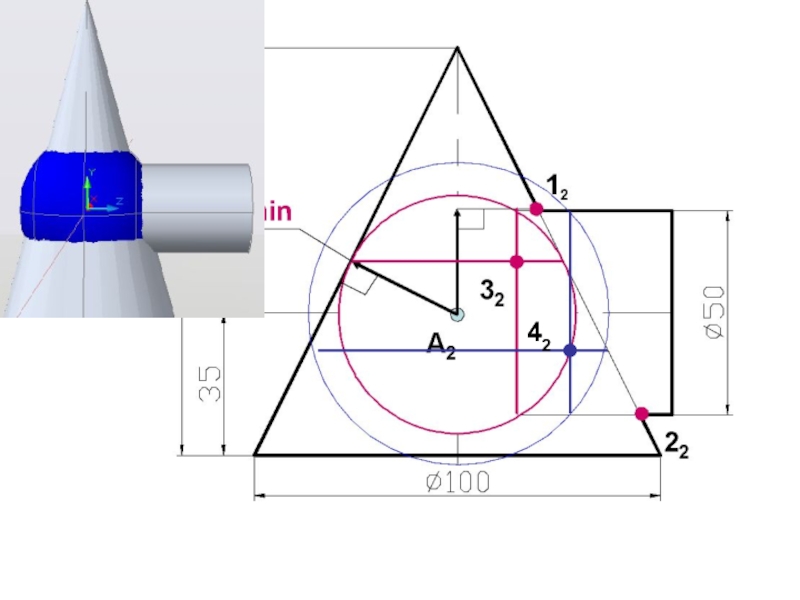
- 77. 42
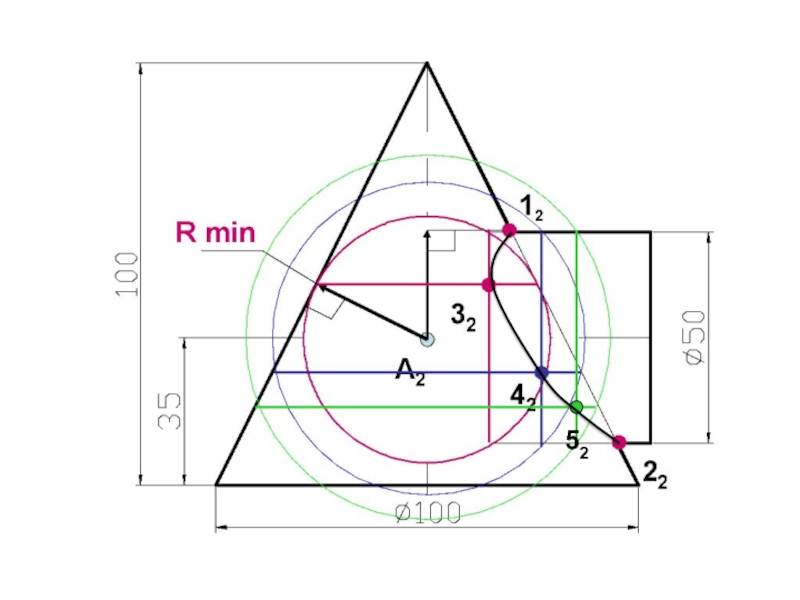
- 78. 52
- 79. ЧАСТНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
- 80. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА ОПИСАННЫЕ ИЛИ ВПИСАННЫЕ
- 81. Слайд 81
- 82. Слайд 82
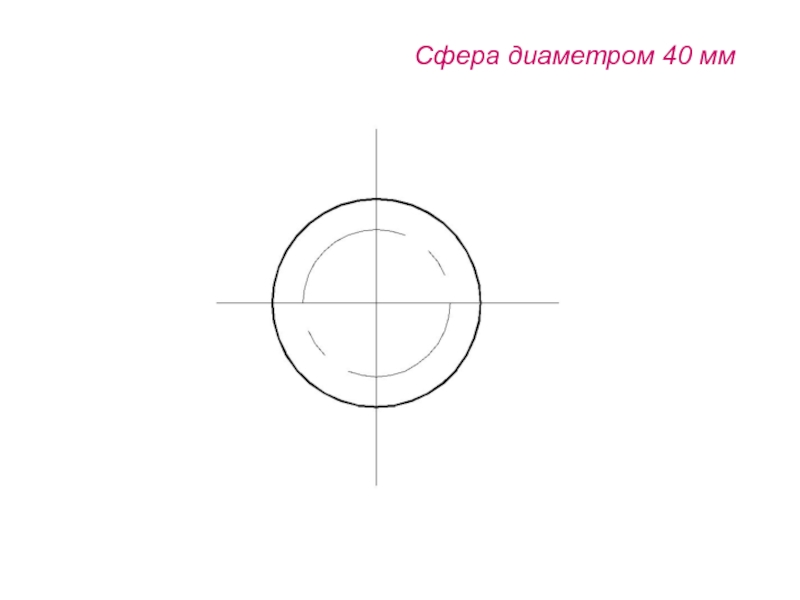
- 83. Сфера диаметром 40 мм
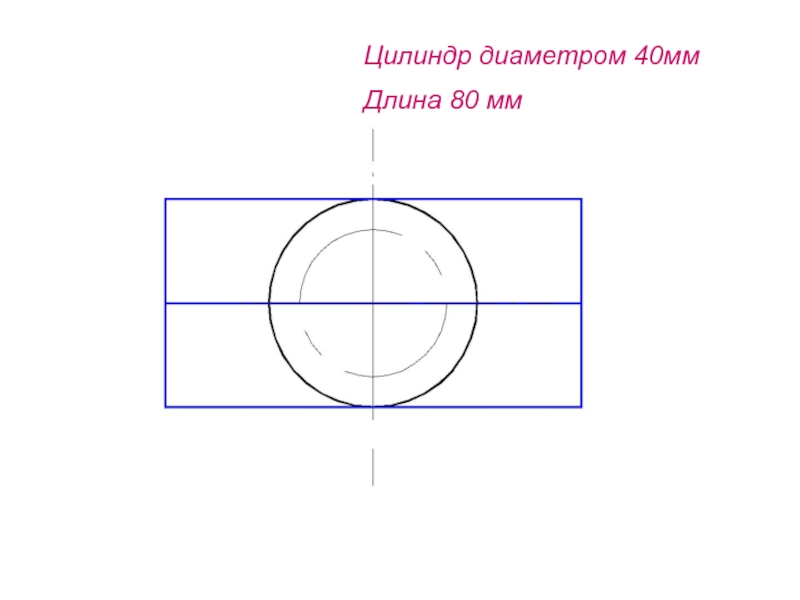
- 84. Цилиндр диаметром 40ммДлина 80 мм
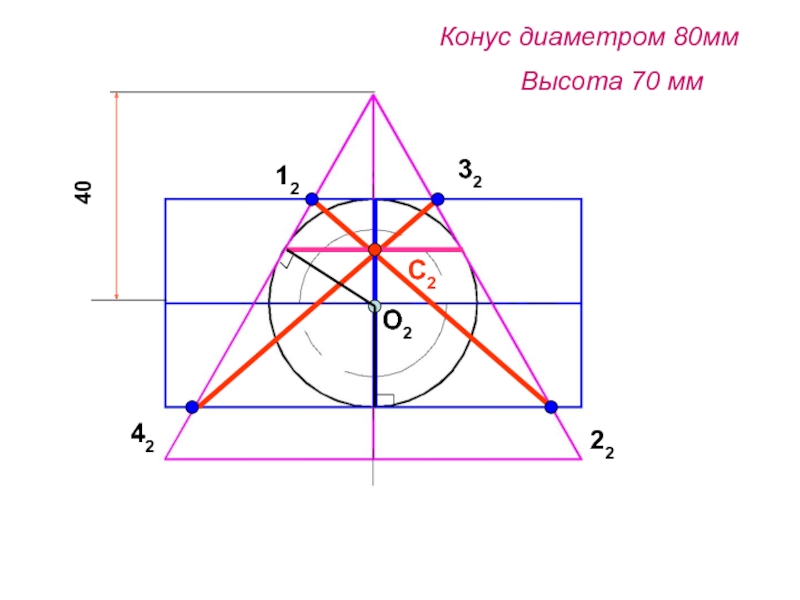
- 85. Конус диаметром 80мм Высота 70 мм40С212223242О2
- 86. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- 87. РАЗВЕРТКА ПОВЕРХНОСТИ – ЭТО ПЛОСКАЯ
- 88. Слайд 88
- 89. 1. ТОЧНЫЕ – ПОСТРОЕННЫЕ ГРАФОАНАЛИТИЧЕСКИМ СПОСОБОМ2. ПРИБЛИЖЕННЫЕ
- 90. СПОСОБЫ ПОСТРОЕНИЯ РАЗВЕРТОК ПОВЕРХНОСТЕЙ АППРОКСИМАЦИЯ –
- 91. АППРОКСИМАЦИЯ В КРУГОВОЕ ОСНОВАНИЕ
- 92. Способ нормального сеченияНормальное сечение - это сечение поверхности плоскостью перпендикулярной оси вращения или высоте поверхности
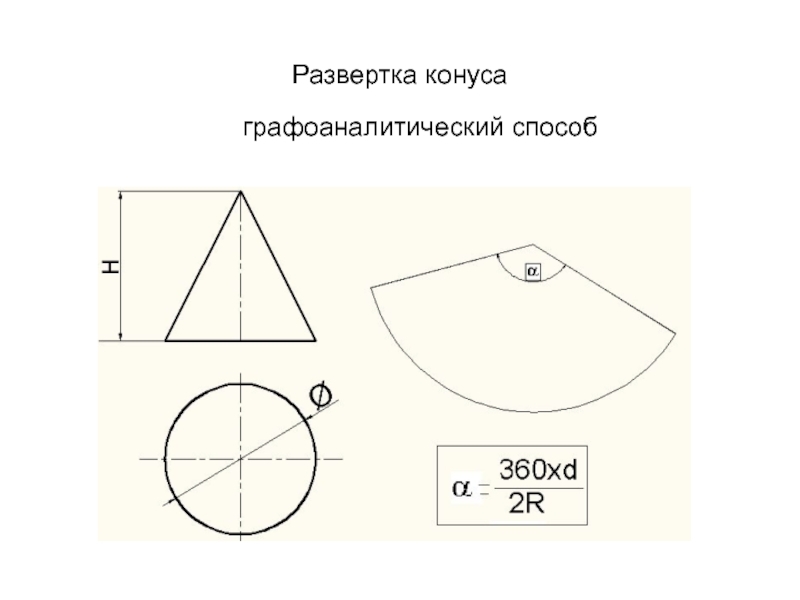
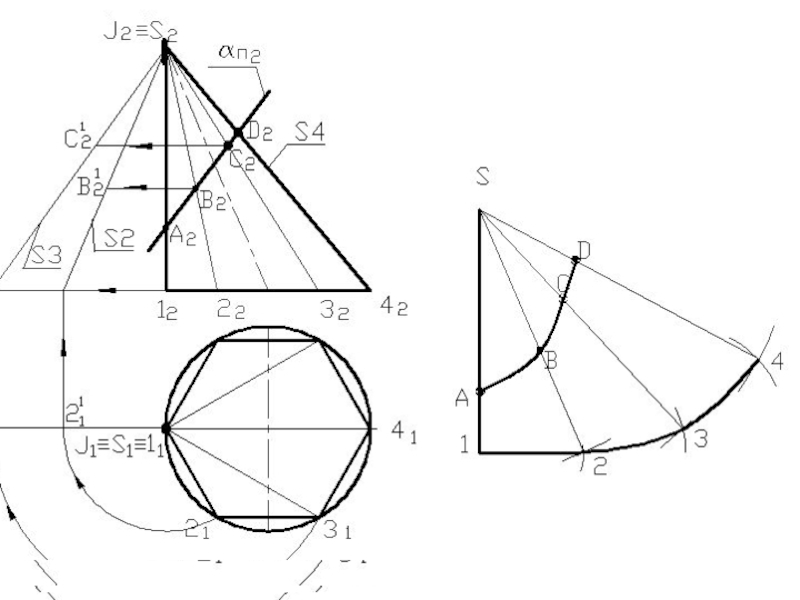
- 93. Развертка конуса графоаналитический способ
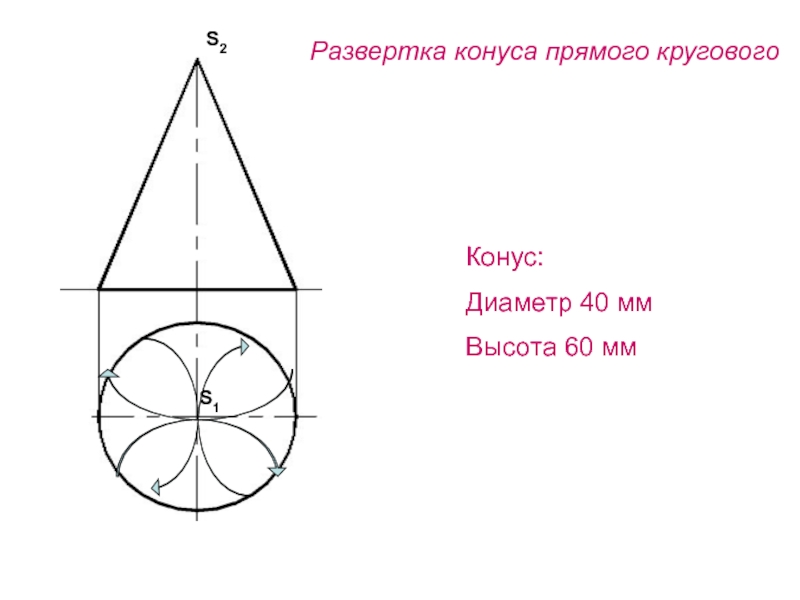
- 94. Развертка конуса прямого кругового Конус: Диаметр 40 мм Высота 60 ммS2S1
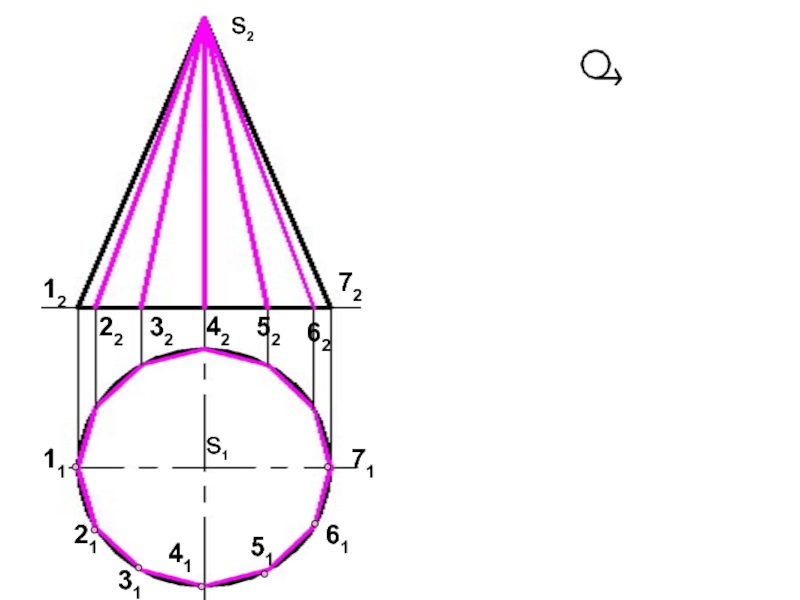
- 95. 1121314151617112223242527262s2s1
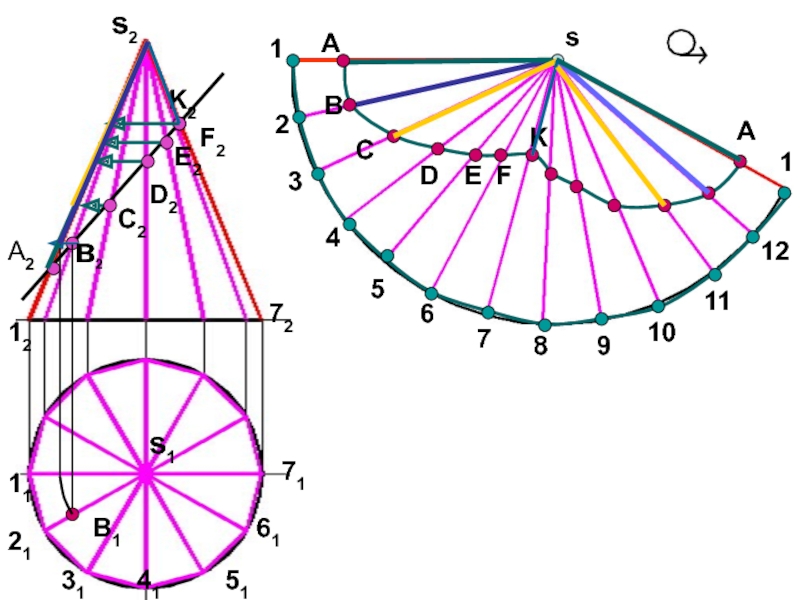
- 96. 112131415161711234567891011121s2s1sА2в2С2D2E2F2K2В1AВСDEFKA1272
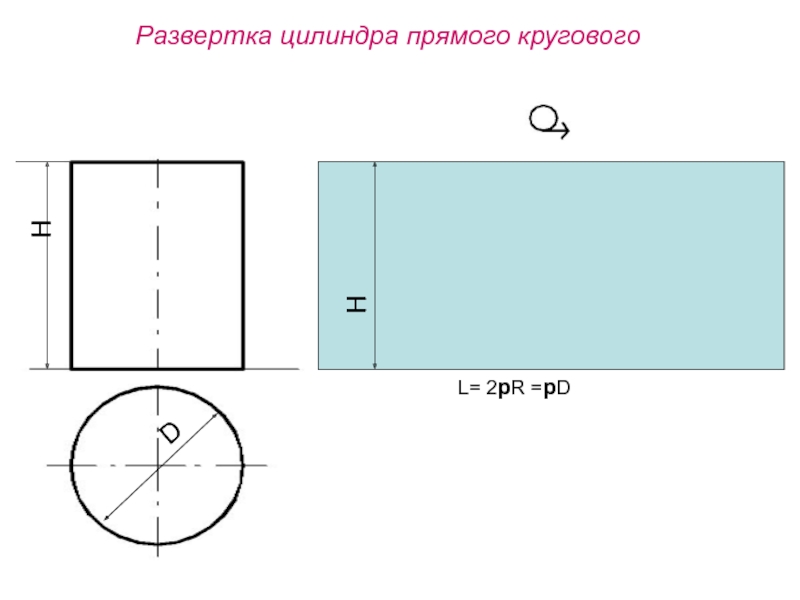
- 97. Развертка цилиндра прямого кругового L= 2pR =pDDHH
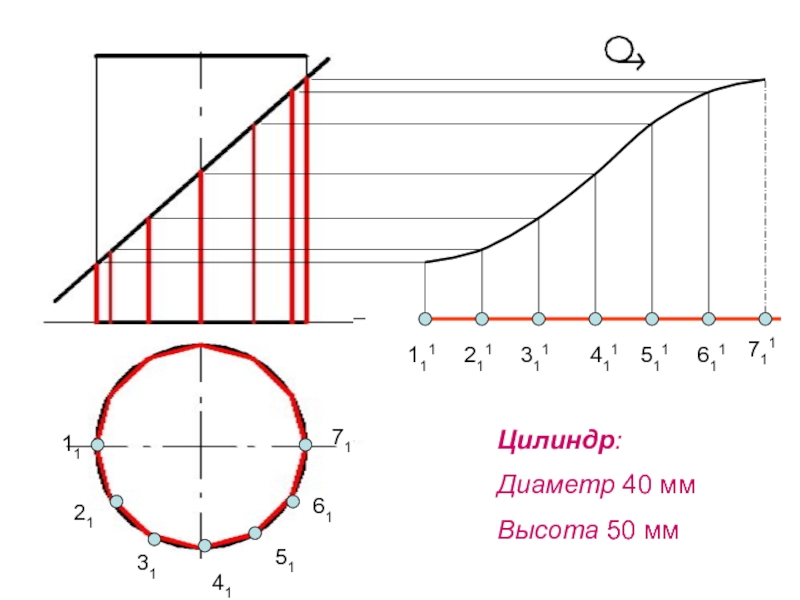
- 98. 11214151617131311411211111611711511 Цилиндр: Диаметр 40 мм Высота 50 мм
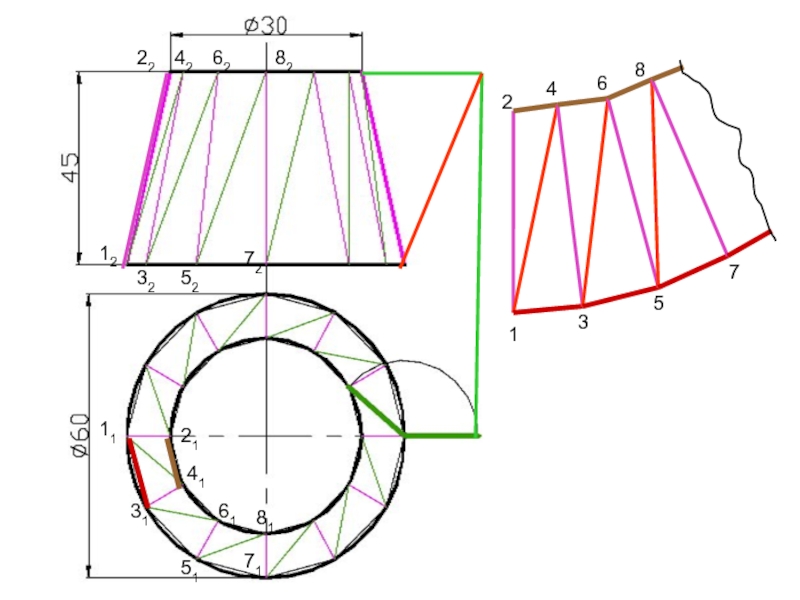
- 99. Способ триангуляцииКонус с недоступной вершиной
- 100. 1122122121423152325141616234658827281717
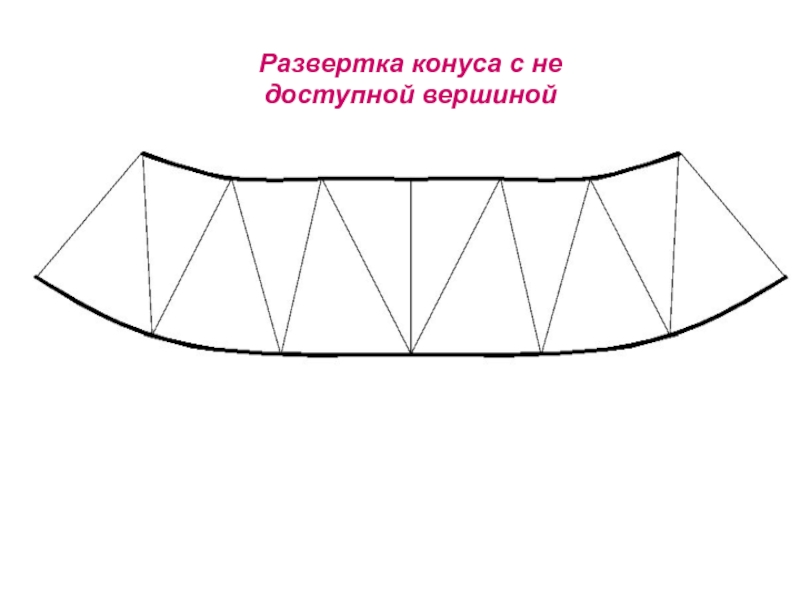
- 101. Развертка конуса с не доступной вершиной
- 102. Дополнительный материал
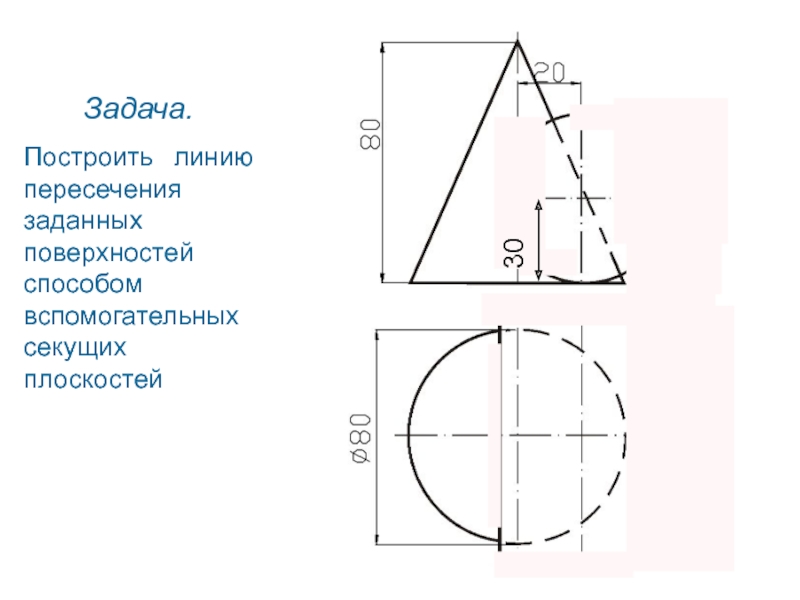
- 103. Задача. Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей30
- 104. Слайд 104
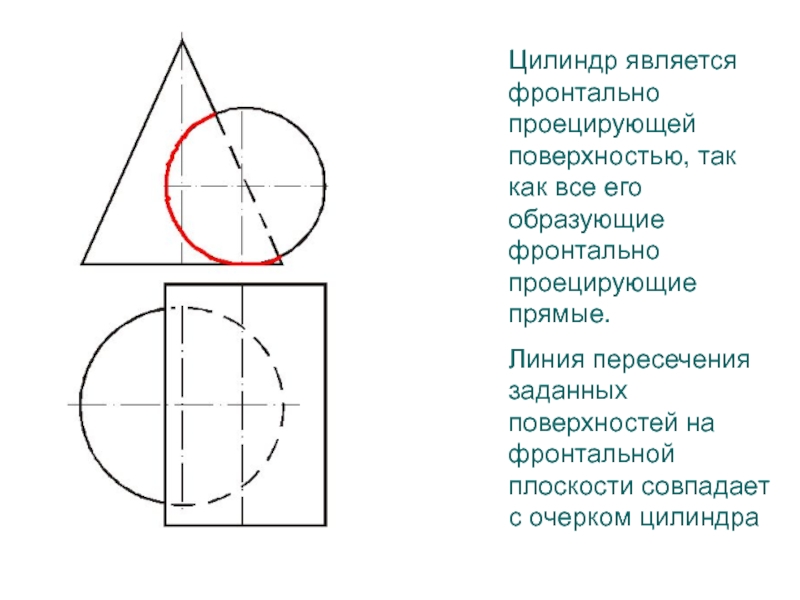
- 105. Цилиндр является фронтально проецирующей поверхностью, так как
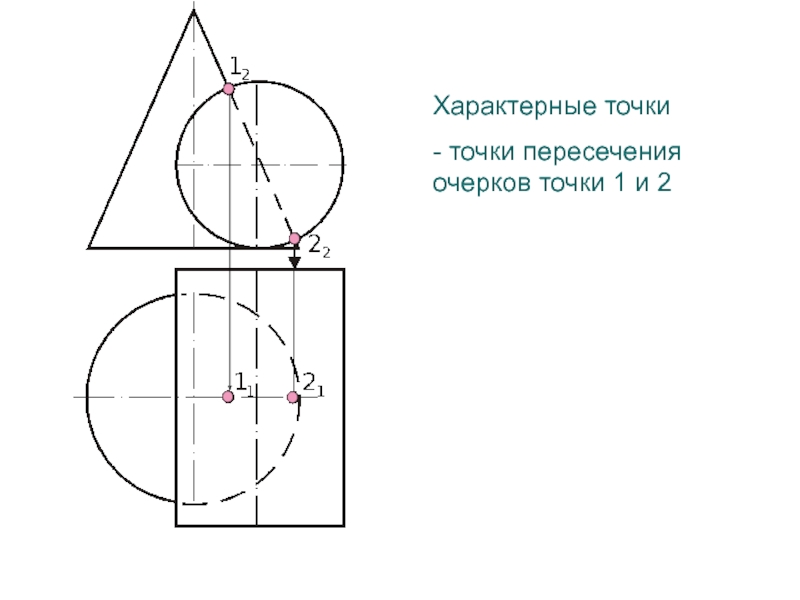
- 106. Характерные точки- точки пересечения очерков точки 1 и 2
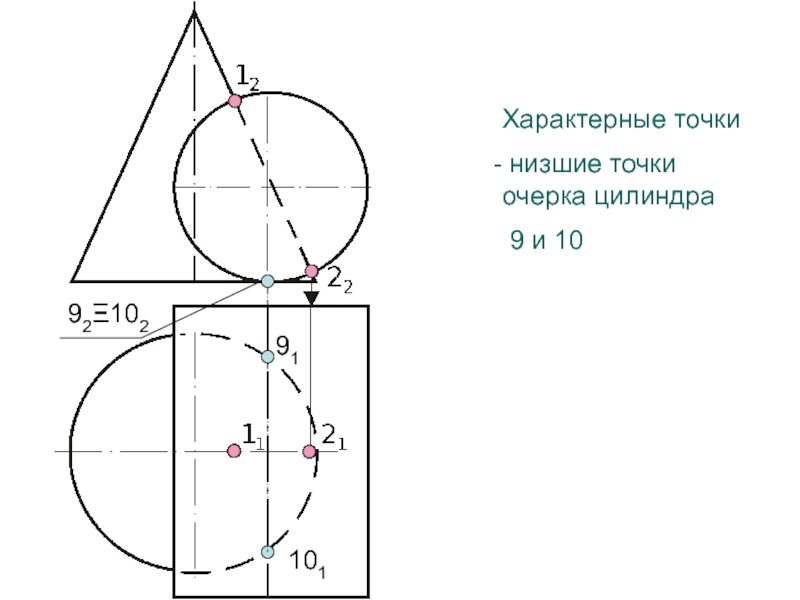
- 107. Характерные точки низшие точки очерка цилиндра 9 и 1092Ξ10291101
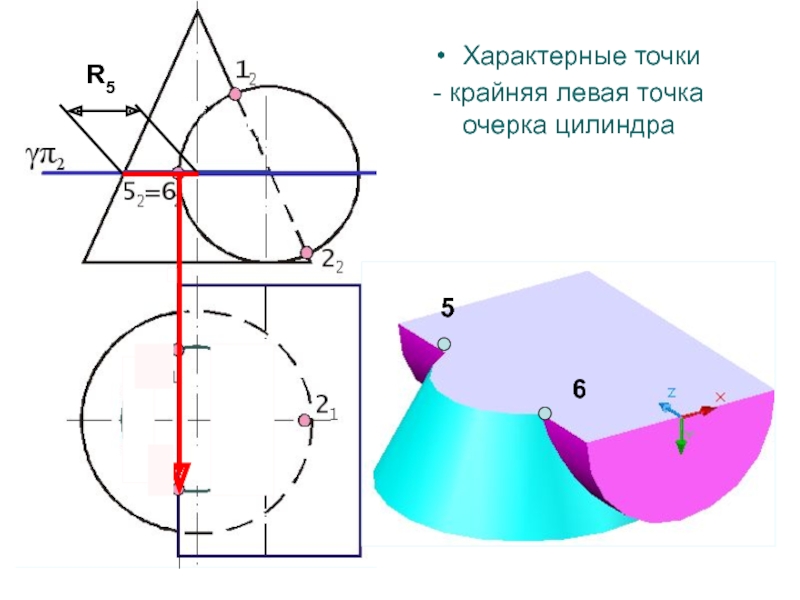
- 108. R556Характерные точки- крайняя левая точка очерка цилиндра
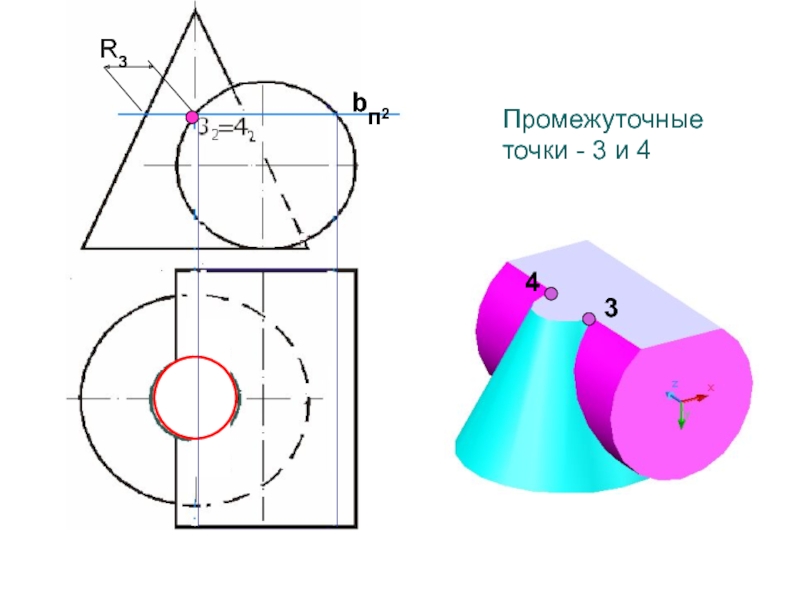
- 109. Промежуточные точки - 3 и 4bп2R343
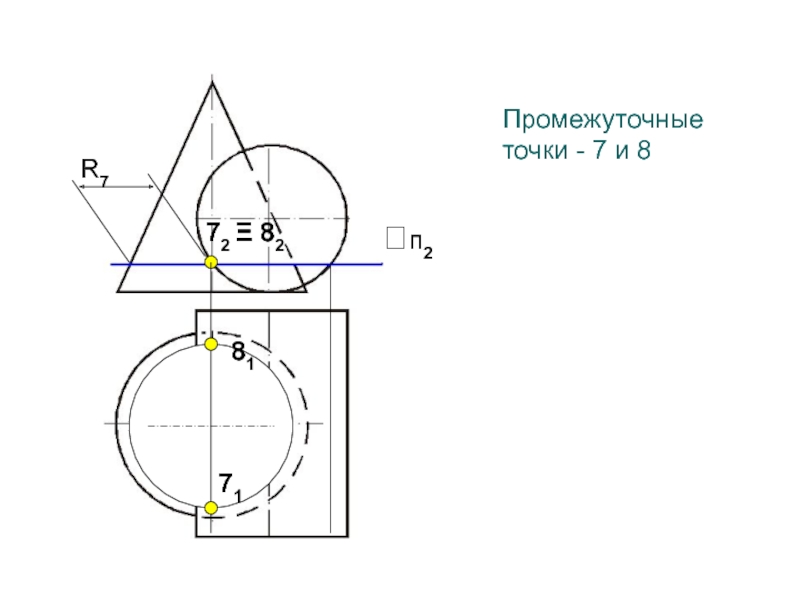
- 110. Промежуточные точки - 7 и 8R7817172 Ξ 82п2
- 111. Слайд 111
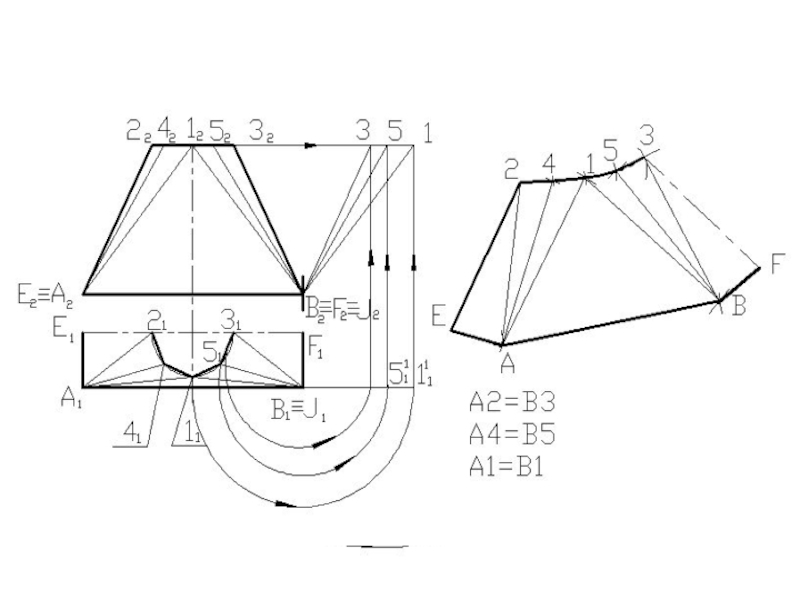
- 112. Развертка переходника
- 113. Слайд 113
- 114. Развертка конуса с одной плоскостью симметрии
- 115. Слайд 115
- 116. СЕЧЕНИЕ КОНУСА ВРАЩЕНИЯ эллипс2212321121αп2Rк31131Rк4141142123113121122232
- 117. 121142322221414113113112132142122112313414
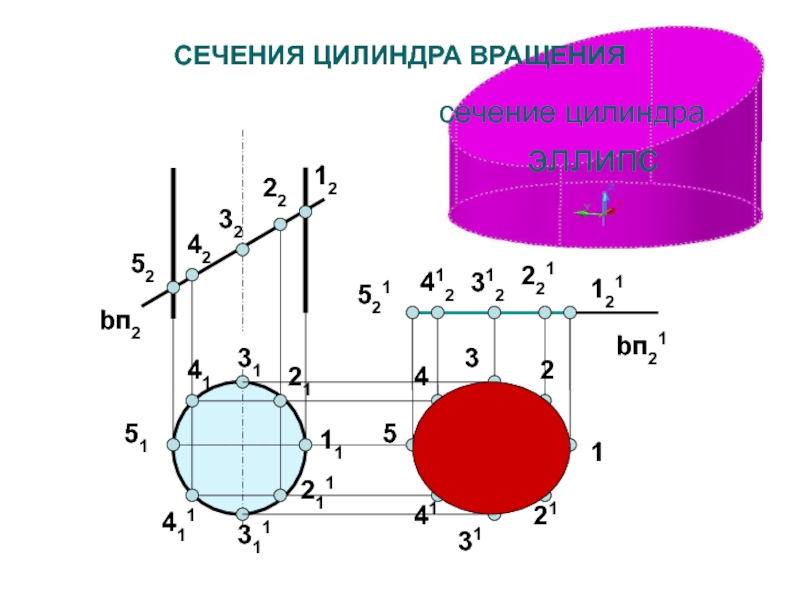
- 118. сечение цилиндра эллипсСЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯbп211212111122112212122213233131131231411424141241451552152bп2
- 119. СЕЧЕНИЕ СФЕРЫαп212112221323131142bп241141gп25251511
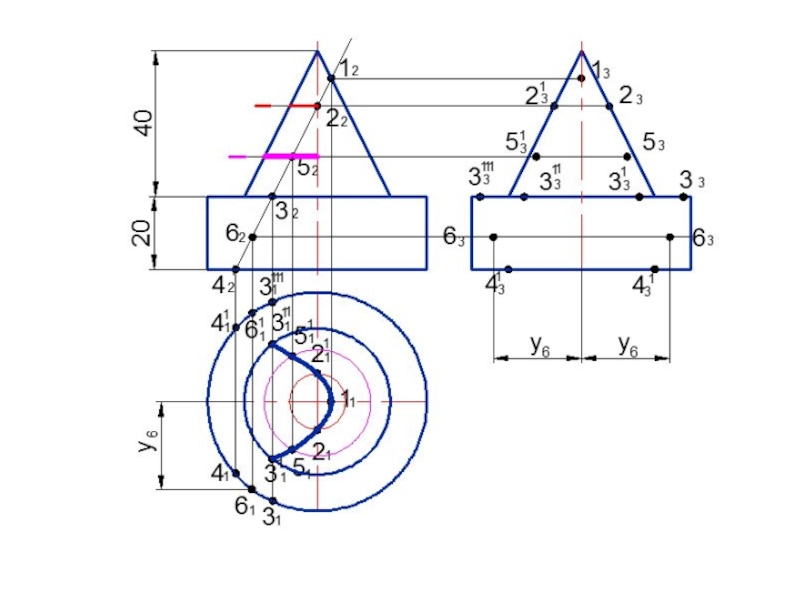
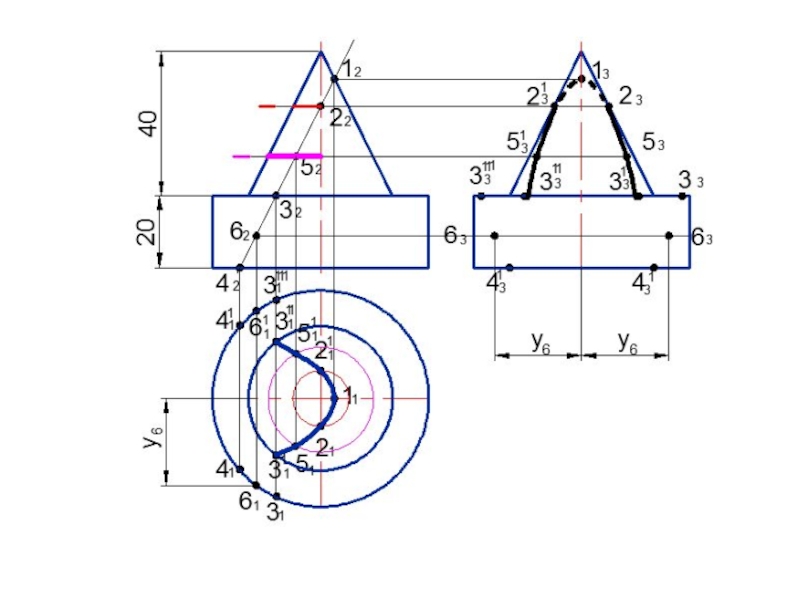
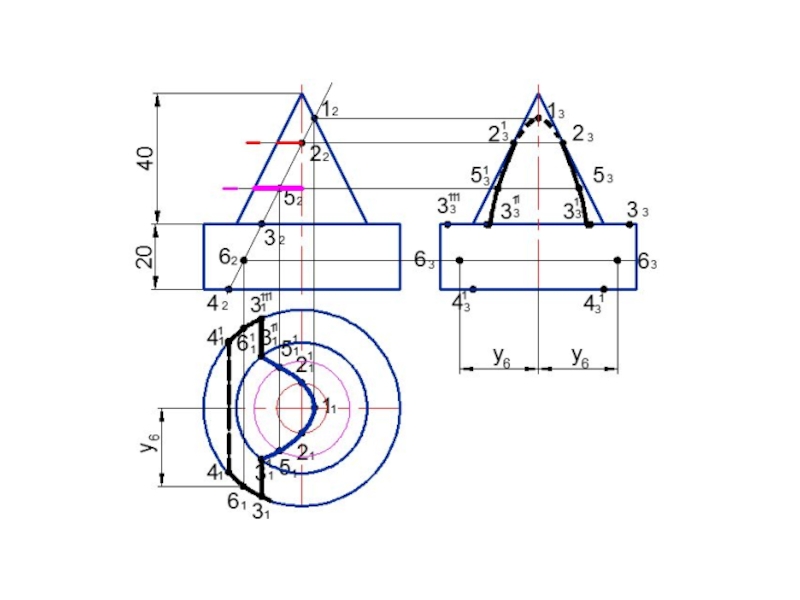
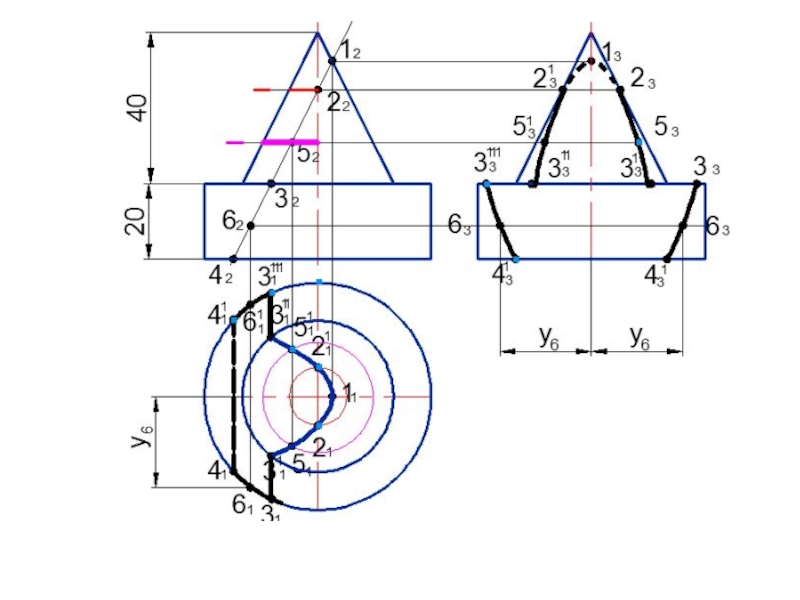
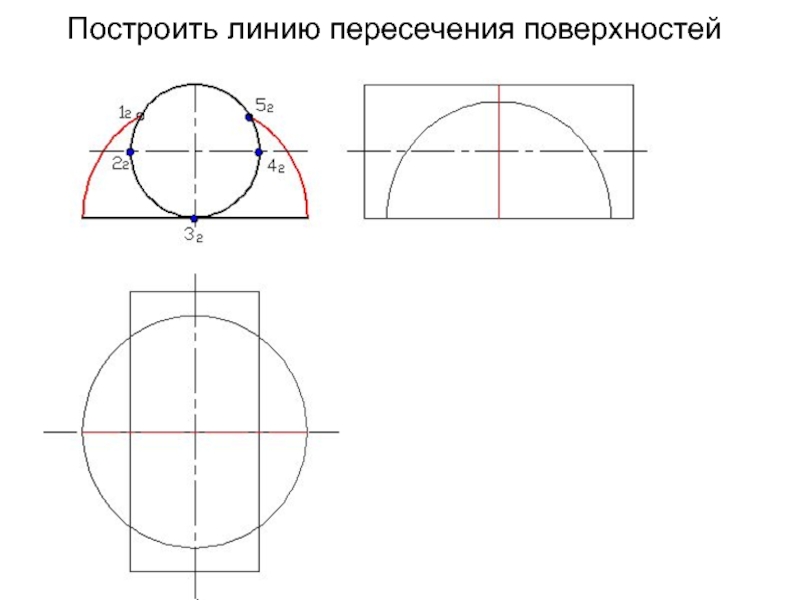
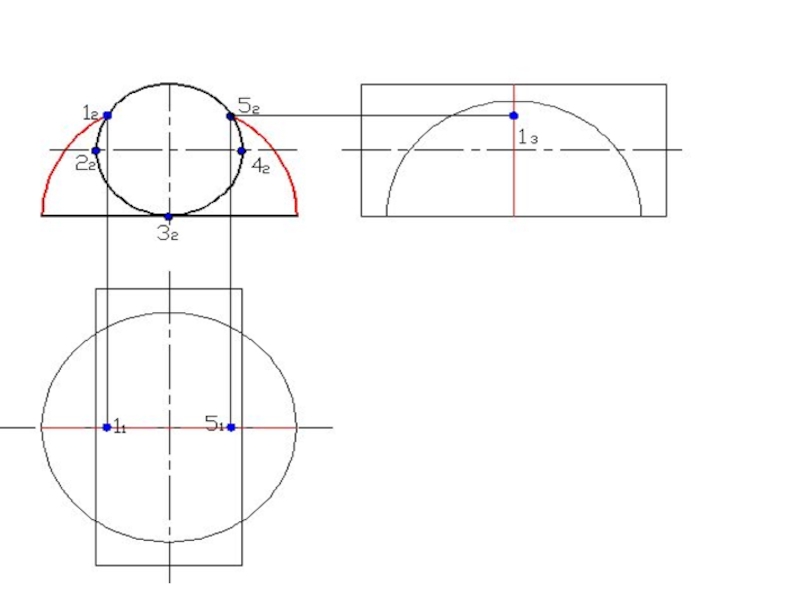
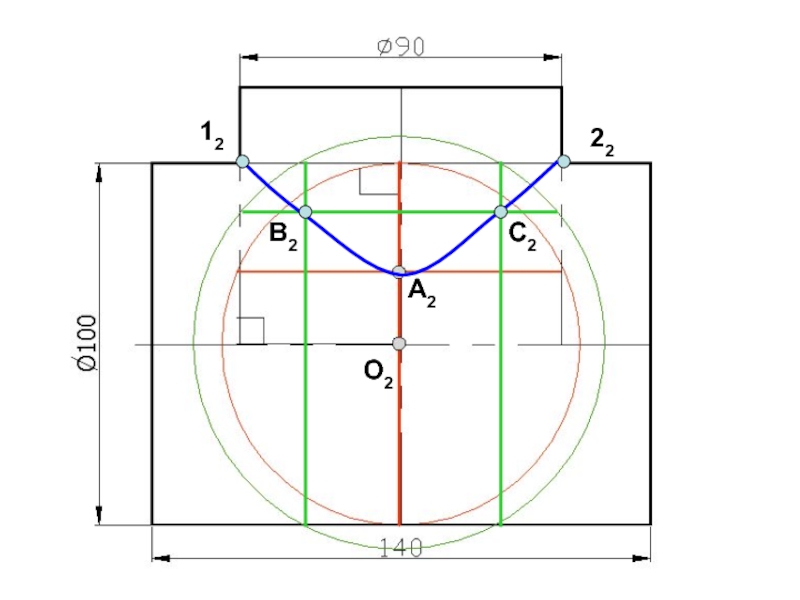
- 120. Построить линию пересечения поверхностей
- 121. О2А2В2С21222
- 122. Скачать презентанцию
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ занимается построением изображений и изучениемпространственных объектов по их изображениям графическими методами
Слайды и текст этой презентации
Слайд 1Уральский государственный технический университет - УПИ
Кафедра
“Инженерная графика”
НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ
Слайд 2 НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ занимается построением изображений и изучением
пространственных объектов по
их изображениям графическими методами
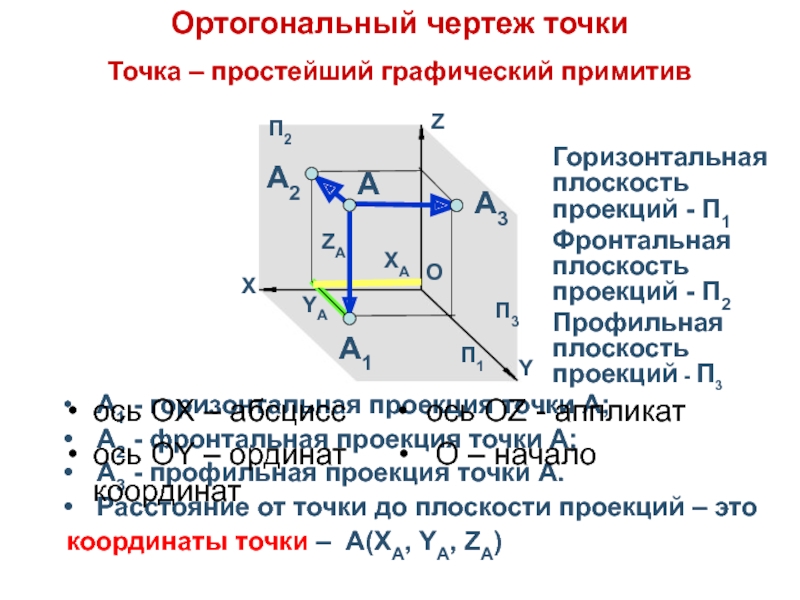
Слайд 3 А1 - горизонтальная проекция точки А;
А2 - фронтальная
проекция точки А;
А3 - профильная проекция точки А.
Расстояние
от точки до плоскости проекций – этокоординаты точки – А(XА, YА, ZА)
X
Y
O
П1
П3
П2
XA
Z
А
А1
А2
А3
YA
ZA
Ортогональный чертеж точки
Точка – простейший графический примитив
ось ОX – абсцисс • ось ОZ - аппликат
ось ОY – ординат • О – начало координат
Горизонтальная плоскость проекций - П1
Фронтальная плоскость проекций - П2
Профильная плоскость проекций - П3
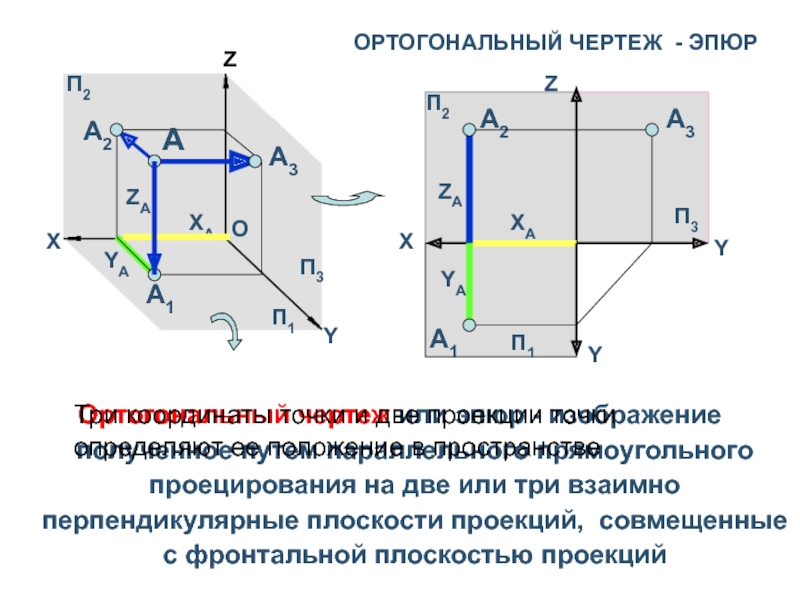
Слайд 4ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ - ЭПЮР
Ортогональный чертеж или эпюр - изображение полученное
путем параллельного прямоугольного проецирования на две или три взаимно перпендикулярные
плоскости проекций, совмещенные с фронтальной плоскостью проекцийZ
Y
Y
X
П3
П1
П2
XA
А2
А3
YA
ZA
X
Y
O
П1
П3
П2
XA
Z
А
А1
А2
А3
YA
ZA
А1
Три координаты точки и две проекции точки определяют ее положение в пространстве
Слайд 5ВИДЫ ПРЯМЫХ ЛИНИЙ
Прямые частного положения
Прямые общего положения
Ортогональный чертеж прямой
линии
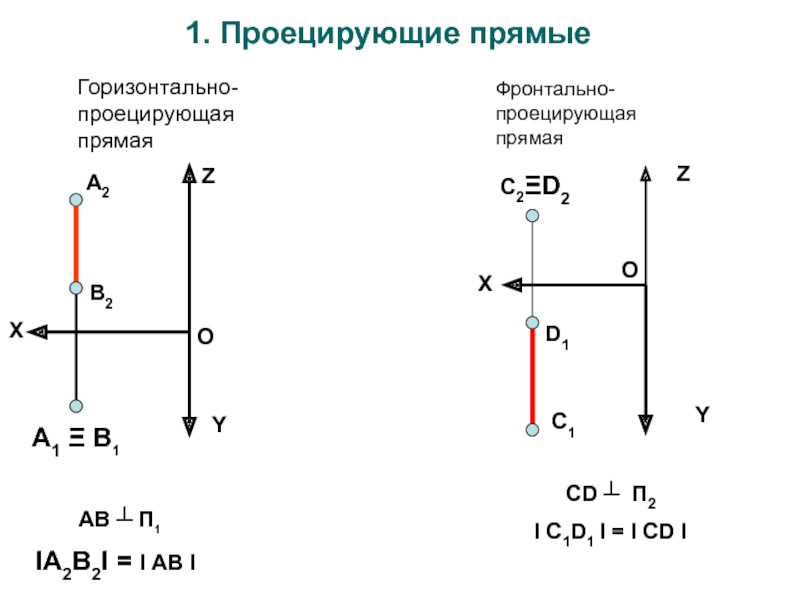
Слайд 6 Прямые частного положения:
• ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ – прямые
перпендикулярные плоскостям проекций
• ЛИНИИ УРОВНЯ – прямые
параллельные плоскостям проекций;
Слайд 71. Проецирующие прямые
Z
X
Y
А1 Ξ B1
B2
А2
О
AB ┴ П1
IА2В2I
= I АВ I
Горизонтально-проецирующая
прямая
Фронтально-проецирующая прямая
X
C1
C2ΞD2
D1
О
Z
Y
CD ┴ П2
I C1D1 I =
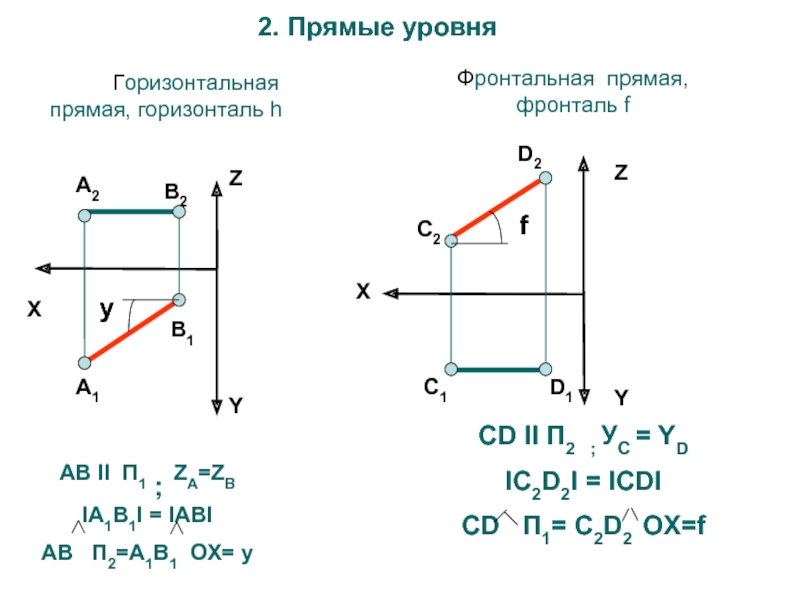
I CD I
Слайд 82. Прямые уровня
Горизонтальная прямая, горизонталь h
X
Z
Y
А2
А1
В2
В1
AВ II П1
; ZА=ZB
IА1В1I = IАВI
АВ П2=А1В1 OX= y
y
Фронтальная
прямая, фронталь fX
Z
Y
C2
C1
D2
D1
f
CD II П2 ; УС = YD
IС2D2I = ICDI
CD П1= С2D2 OX=f
Слайд 9 Ортогональный чертеж прямых линий общего положения
не параллельные и не
перпендикулярные плоскостям проекций
Слайд 10ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ ПЛОСКОСТИ
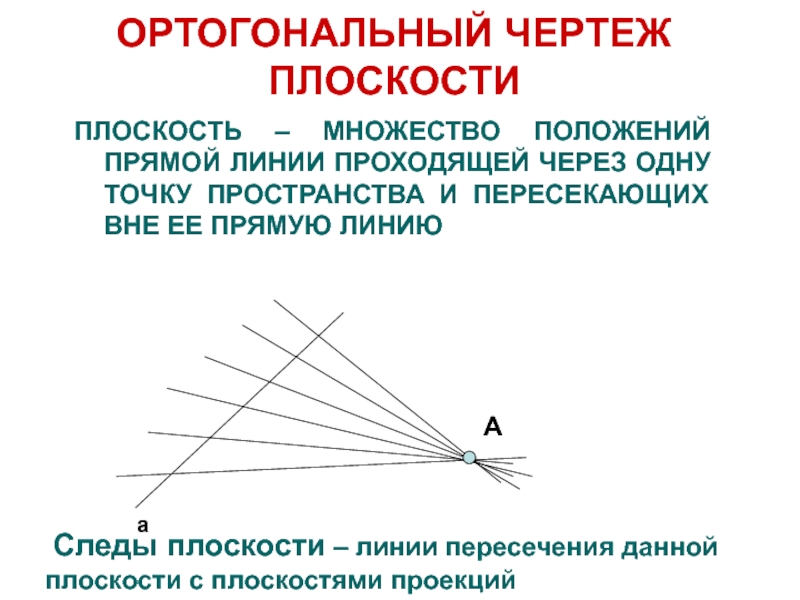
ПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ ЛИНИИ ПРОХОДЯЩЕЙ ЧЕРЕЗ
ОДНУ ТОЧКУ ПРОСТРАНСТВА И ПЕРЕСЕКАЮЩИХ ВНЕ ЕЕ ПРЯМУЮ ЛИНИЮ
A
a
Следы
плоскости – линии пересечения данной плоскости с плоскостями проекций
Слайд 11Y
Z
X
aп1
aП3
aП2
ax
ay
az
a
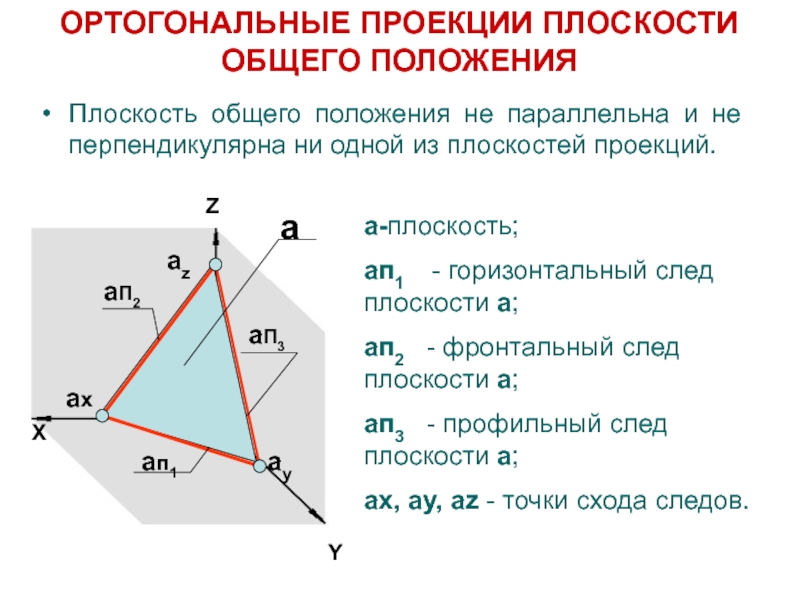
a-плоскость;
aп1 - горизонтальный след плоскости a;
aп2 -
фронтальный след плоскости a;
aп3 - профильный след плоскости a;
ax,
ay, az - точки схода следов. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Слайд 12ПЛОСКОСТИ УРОВНЯ плоскости параллельные плоскостям проекций –
ПЛОСКОСТИ ПРОЕЦИРУЮЩИЕ плоскости
перпендикулярные плоскостям проекций –
Плоскости частного положения
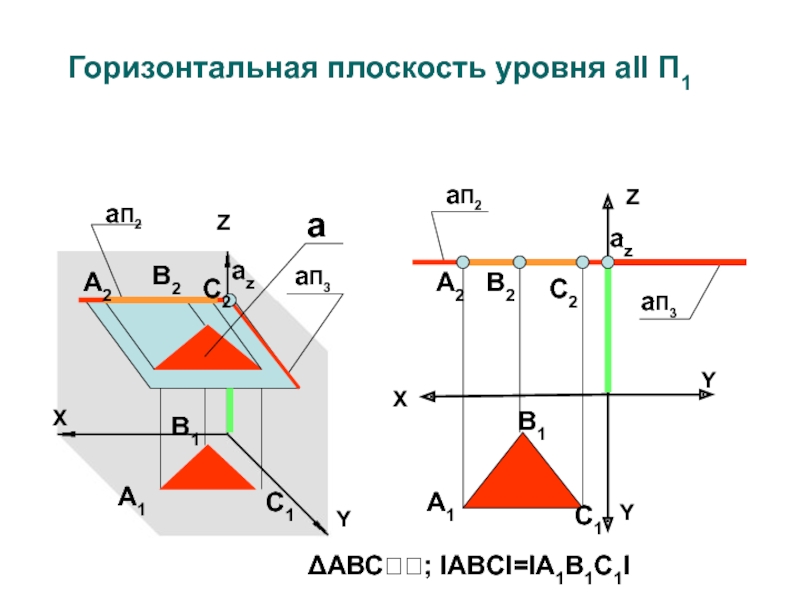
Слайд 13Горизонтальная плоскость уровня aII П1
Z
X
Y
Y
aП2
aП3
az
Y
Z
X
aП3
aП2
az
a
А1
В1
С1
А2
В2
С2
А1
С1
В1
А2
В2
С2
ΔАВС; IABCI=IA1B1C1I
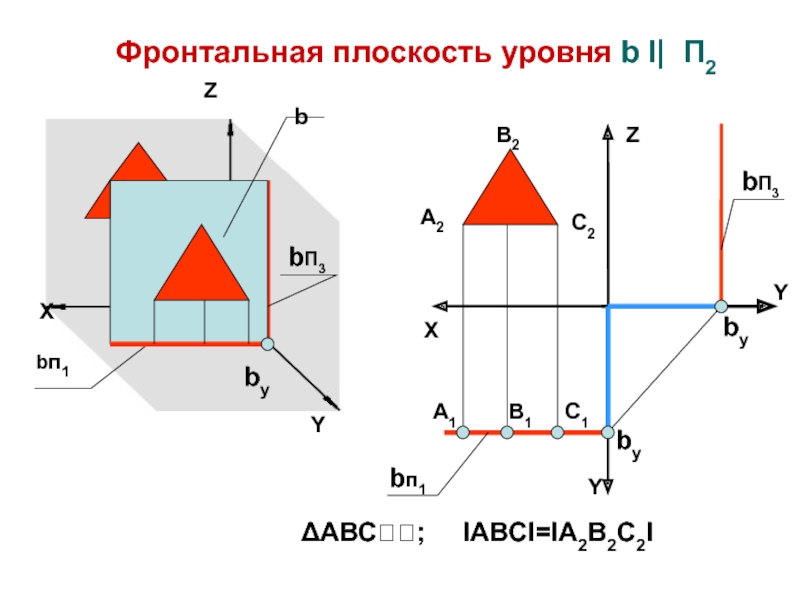
Слайд 14Z
X
Y
Y
bп1
bП3
by
Y
Z
X
bп1
bП3
by
by
Фронтальная плоскость уровня b I| П2
А1
В1
С1
С2
В2
А2
b
ΔАВС; IABCI=IA2B2C2I
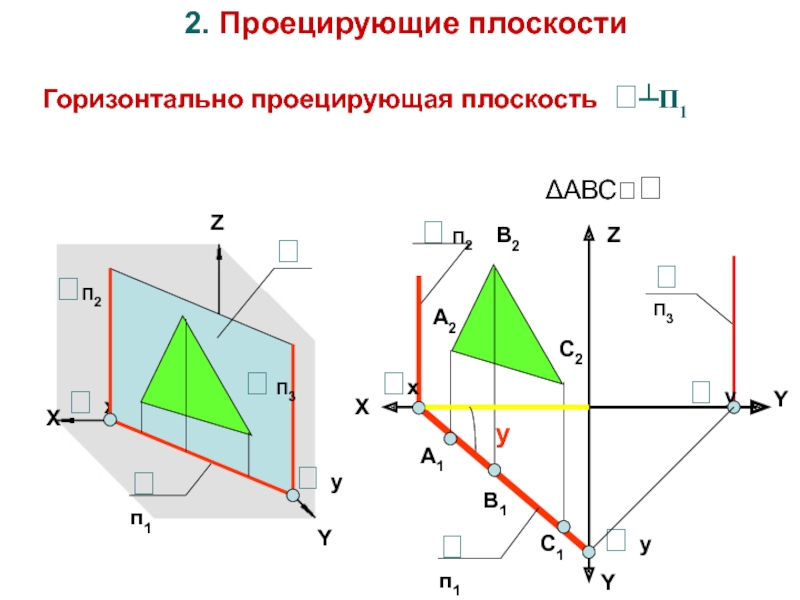
Слайд 152. Проецирующие плоскости
Горизонтально проецирующая плоскость ┴П1
X
Y
Y
П2
П3
Z
X
п1
П2
x
x
Z
п1
П3
Y
y
y
y
y
А1
В1
С1
А2
В2
С2
ΔАВС
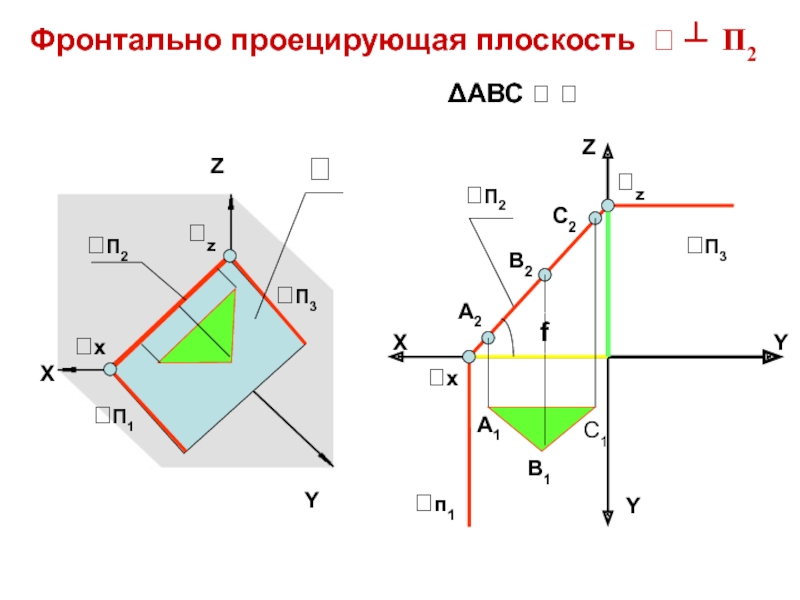
Слайд 16Фронтально проецирующая плоскость ┴ П2
Z
X
Y
Y
П2
п1
x
Y
Z
X
П2
z
П3
П1
П3
z
x
А2
В2
С2
А1
В1
С1
f
ΔАВС
Слайд 18ПОВЕРХНОСТИ
ПОВЕРХНОСТЬ
МНОЖЕСТВО ПОЛОЖЕНИЙ ЛИНИИ ПЕРЕМЕЩАЮЩЕЙСЯ В ПРОСТРАНСТВЕ ПО ОПРЕДЕЛЕННОМУ ЗАКОНУ
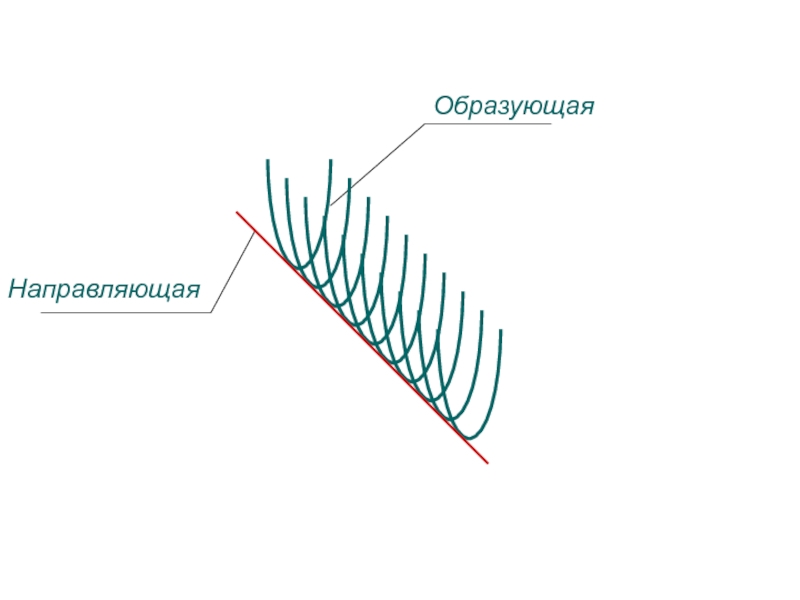
ЛИНИЯ ПЕРЕМЕЩАЮЩАЯСЯ
В ПРОСТРАНСТВЕ - ОБРАЗУЮЩАЯ
ЛИНИЯ ПО КОТОРОЙ ПРОИСХОДИТ ПЕРЕМЕЩЕНИЕ - НАПРАВЛЯЮЩАЯ
Слайд 20ОЧЕРК ПОВЕРХНОСТИ
Очерк поверхности при ортогональном проецировании – это границы проекций
поверхности или
следы проецирующей поверхности, огибающей заданную поверхность, на
плоскостях проекций Графический способ задания поверхности
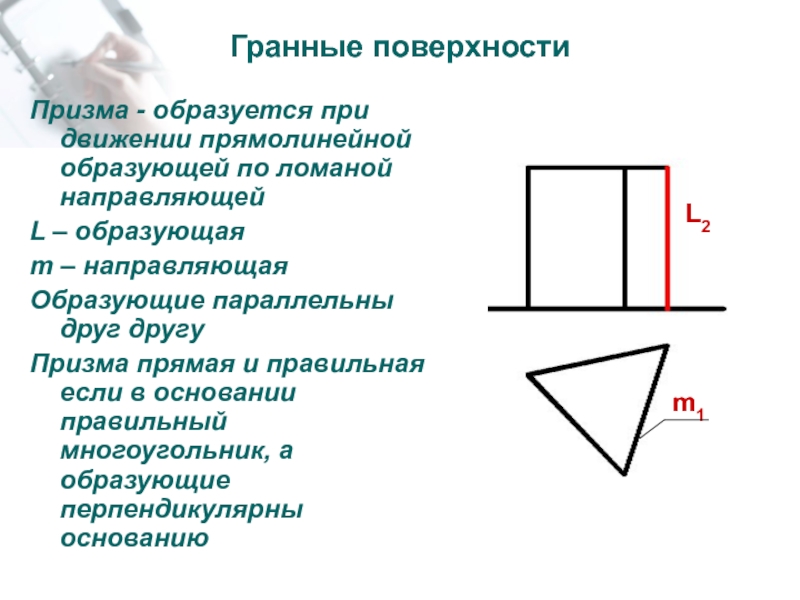
Слайд 24Гранные поверхности
Призма - образуется при движении прямолинейной образующей по ломаной
направляющей
L – образующая
m – направляющая
Образующие параллельны друг другу
Призма прямая и
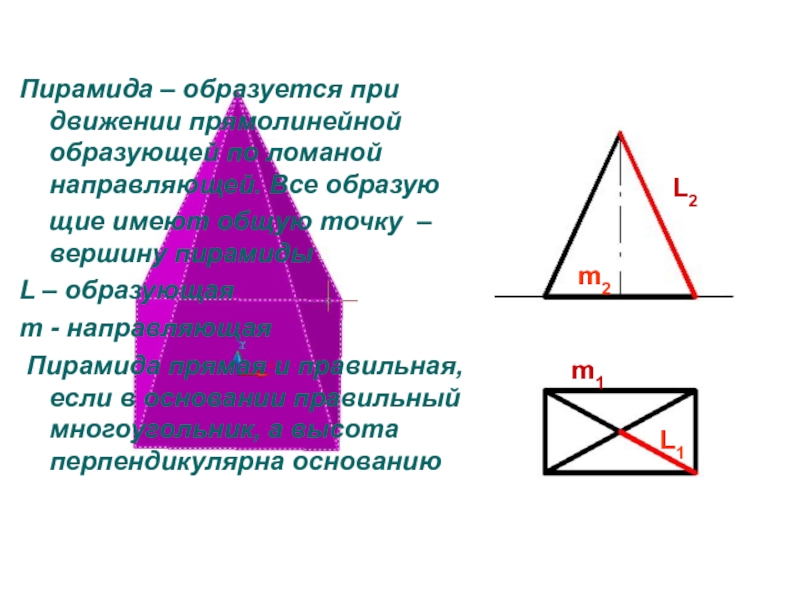
правильная если в основании правильный многоугольник, а образующие перпендикулярны основанию
Слайд 25Пирамида – образуется при движении прямолинейной образующей по ломаной направляющей.
Все образую
щие имеют общую точку – вершину пирамиды
L
– образующаяm - направляющая
Пирамида прямая и правильная, если в основании правильный многоугольник, а высота перпендикулярна основанию
m2
L1
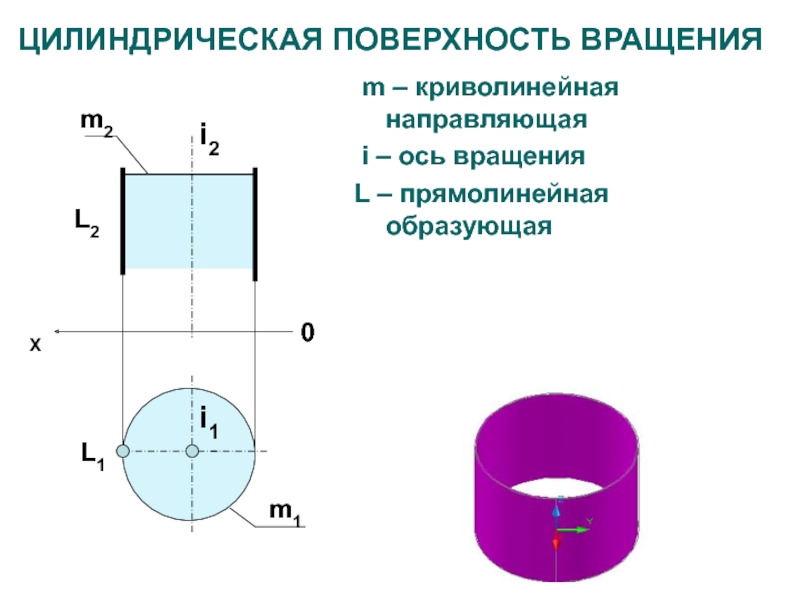
Слайд 26ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ
L2
i2
i1
L1
m – криволинейная направляющая
i – ось вращения
L – прямолинейная образующая
m1
m2
X
0
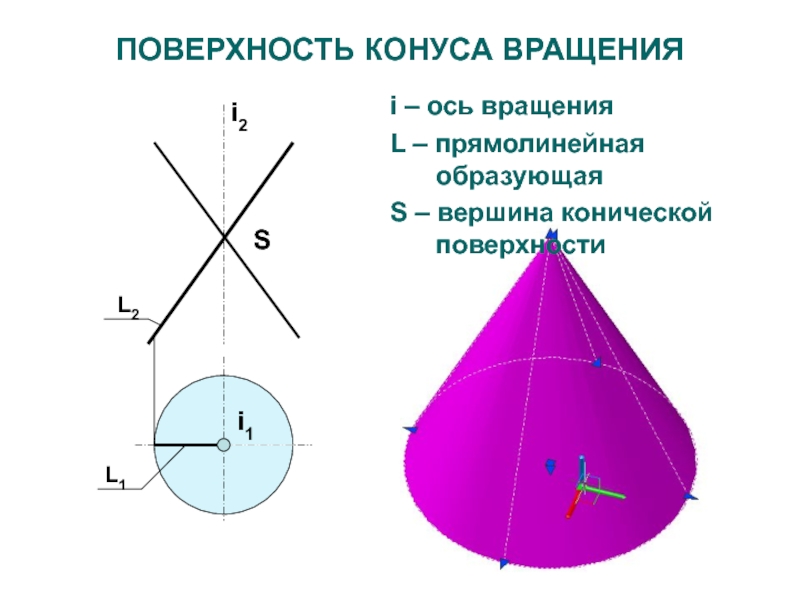
Слайд 27ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ
i – ось вращения
L – прямолинейная
образующая
S – вершина конической поверхности
L2
L1
i2
i1
S
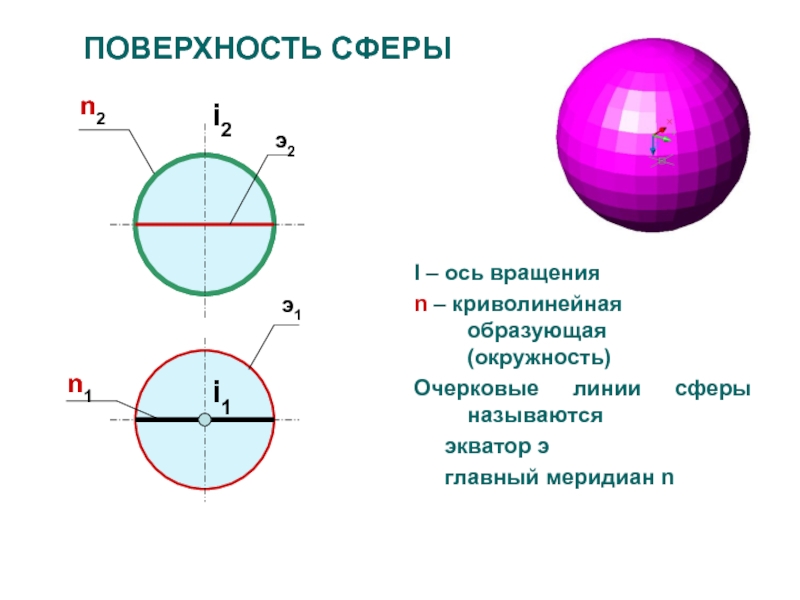
Слайд 28ПОВЕРХНОСТЬ CФЕРЫ
I – ось вращения
n – криволинейная образующая (окружность)
Очерковые линии
сферы называются
экватор э
главный меридиан
nn2
n1
i2
i1
э2
э1
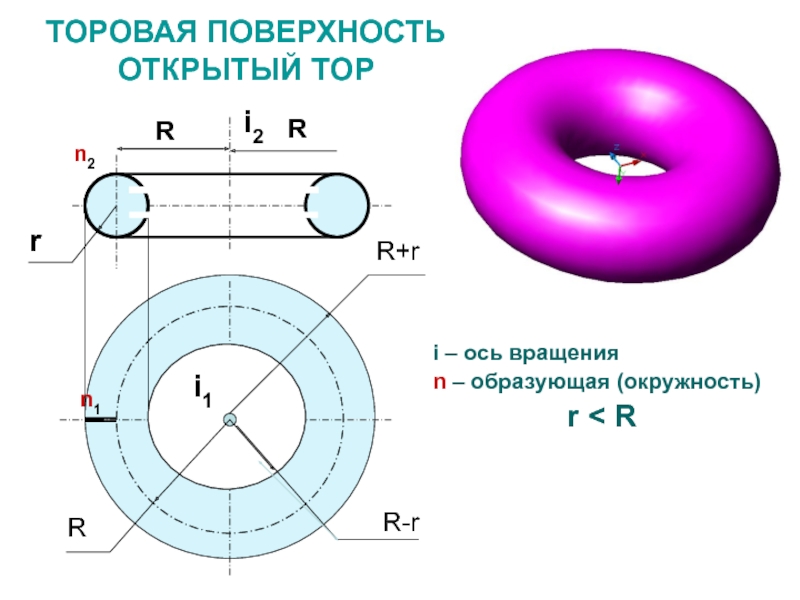
Слайд 29ТОРОВАЯ ПОВЕРХНОСТЬ
ОТКРЫТЫЙ ТОР
i – ось вращения
n – образующая (окружность)
r
< R
i2
n2
n1
r
R
R-r
R+r
R
I1
i1
R
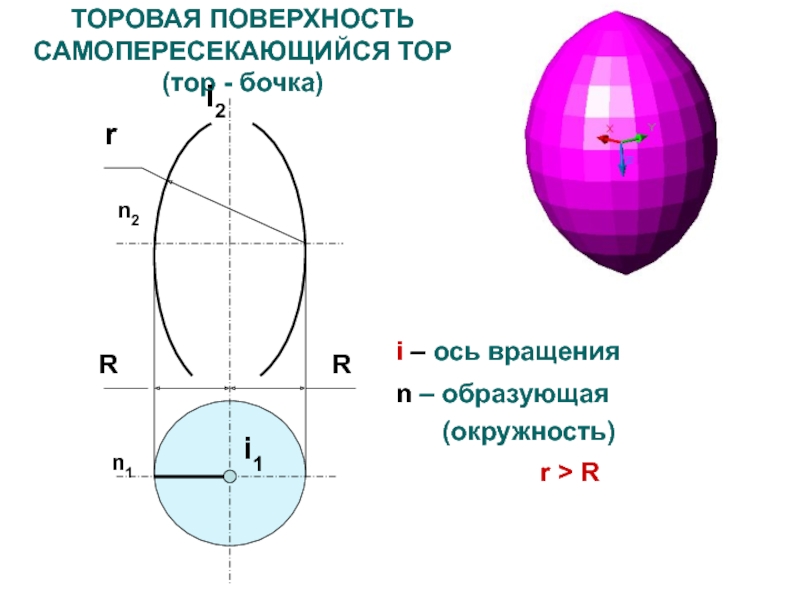
Слайд 30ТОРОВАЯ ПОВЕРХНОСТЬ
САМОПЕРЕСЕКАЮЩИЙСЯ ТОР (тор - бочка)
i – ось
вращения
n – образующая (окружность)
r > R
R
r
i2
n2
n1
i1
R
Слайд 31СЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
- это линия пересечения поверхности и плоскости
или
совокупность
точек одновременно принадлежащих поверхности и плоскости
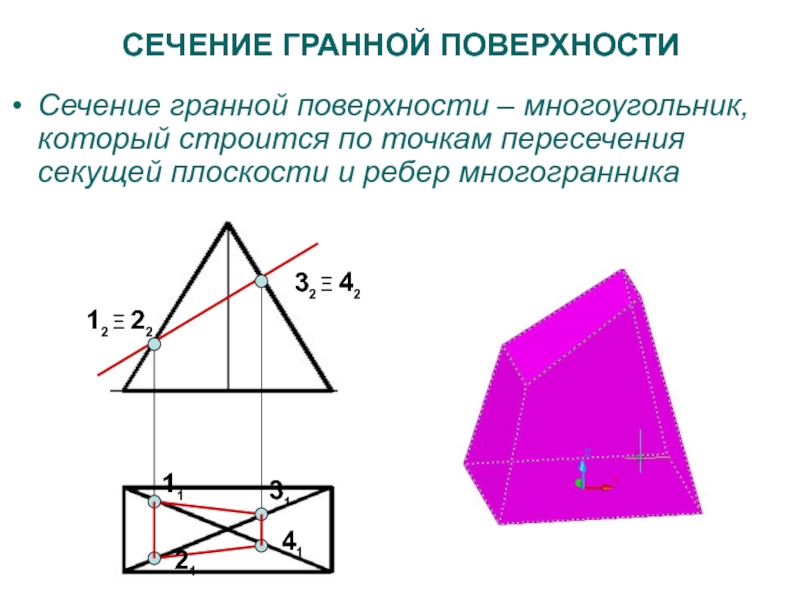
Слайд 32СЕЧЕНИЕ ГРАННОЙ ПОВЕРХНОСТИ
Сечение гранной поверхности – многоугольник, который строится по
точкам пересечения секущей плоскости и ребер многогранника
12 Ξ 22
32 Ξ
4211
21
41
31
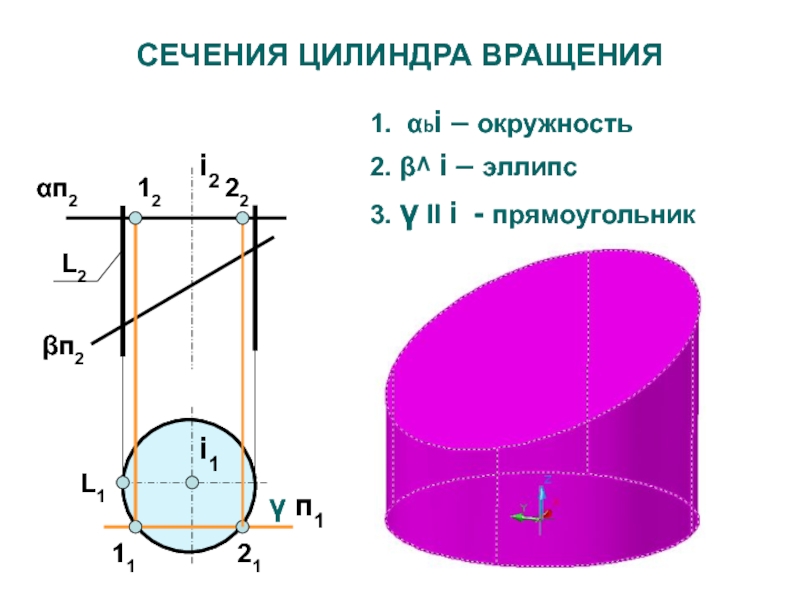
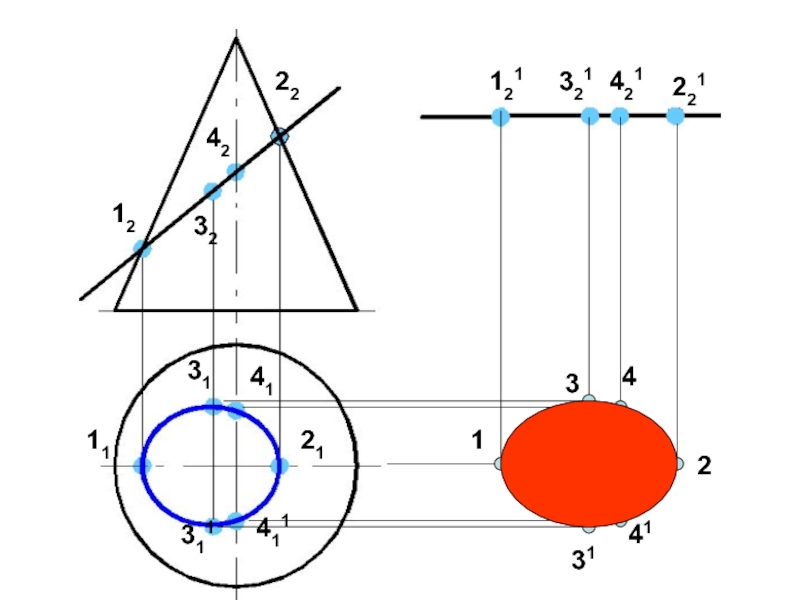
Слайд 33СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
1. αbi – окружность
2. β^ i – эллипс
3.
γ ll i - прямоугольник
L2
i2
i1
L1
αп2
βп2
γ п1
11
21
12
22
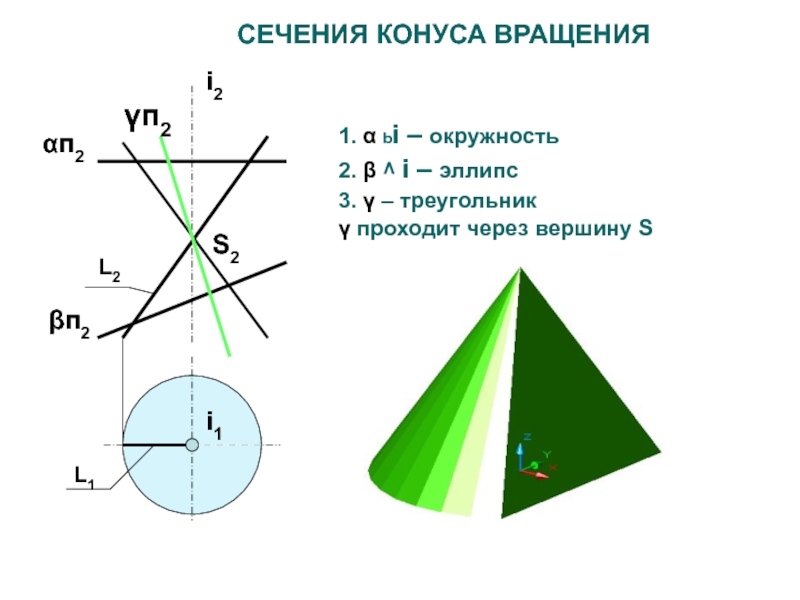
Слайд 34СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ
1. α bi – окружность
2. β ^ i
– эллипс
3. γ – треугольник
γ проходит через вершину S
L2
L1
i2
i1
S2
αп2
βп2
γп2
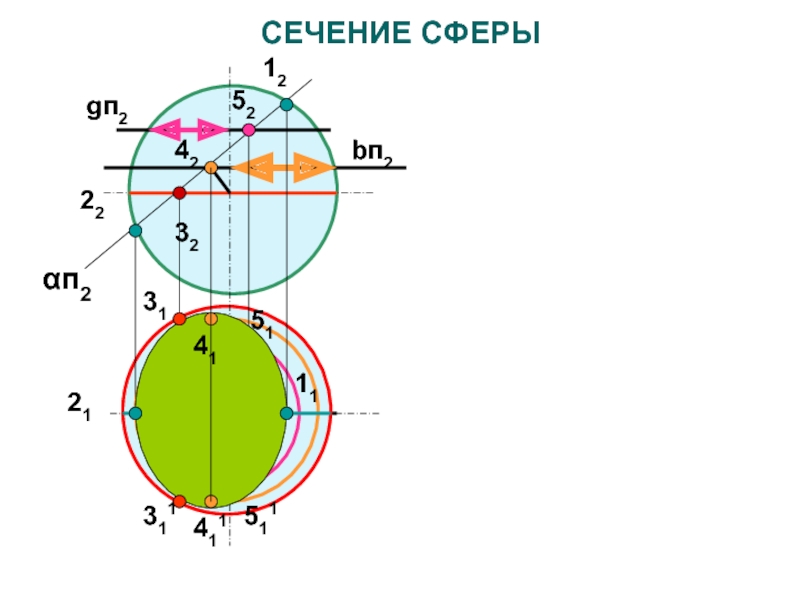
Слайд 36СЕЧЕНИЯ СФЕРЫ
Сечение сферы плоскостью – окружность, которая может
проецироваться как:
прямая линия
окружностьэллипс
Слайд 48Линия пересечения поверхностей -
совокупность точек одновременно принадлежащих
двум пересекающимся поверхностям
Характер линии пересечения зависит от вида поверхностей
Линия пересечения
многогранников ломаная линия
Слайд 49Линия пересечения многогранника и поверхности вращения - сочетание плоских кривых
линий (парабола, гипербола, эллипс и т.д.)
Линия пересечение двух поверхностей второго
порядка - пространственная кривая линия
Слайд 50Алгоритм решения задач
1. Анализ заданных поверхностей
- Определить заданные поверхности
Определить
наличие проецирующей поверхности (цилиндр и призма)
На плоскости
проекций, к которой проецирующая поверхность перпендикулярна, проекция линии пересечения совпадает с очерком проецирующей поверхности
Слайд 512. Определить характерные точки линии пересечения
точки пересечения очерков поверхностей
высшие и
низшие, правые и левые точки поверхностей
наиболее удаленные и приближенные к
плоскостям проекций точкиточки принадлежащие очерковым линиям поверхностей
ВЫБОР СПОСОБА РЕШЕНИЯ ЗАДАЧИ:
- вспомогательные секущие плоскости
вспомогательные секущие концентрические сферы
Слайд 52Способ вспомогательных секущих плоскостей
1. Провести вспомогательную секущую плоскость частного положения.
В сечении поверхностей должны получаться простые геометрические
фигуры – окружности, треугольники, прямоугольники.2. Построить сечения заданных поверхностей вспомогательной секущей плоскостью.
3. Определить точки пересечения построенных сечений. Это искомые точки линии пересечения поверхностей.
Повторение пунктов 1, 2, 3 – n раз
Слайд 534. Соединить линией, полученные точки пересечения.
5. Определить
видимость линии пересечения и очерковых линий заданных поверхностей.
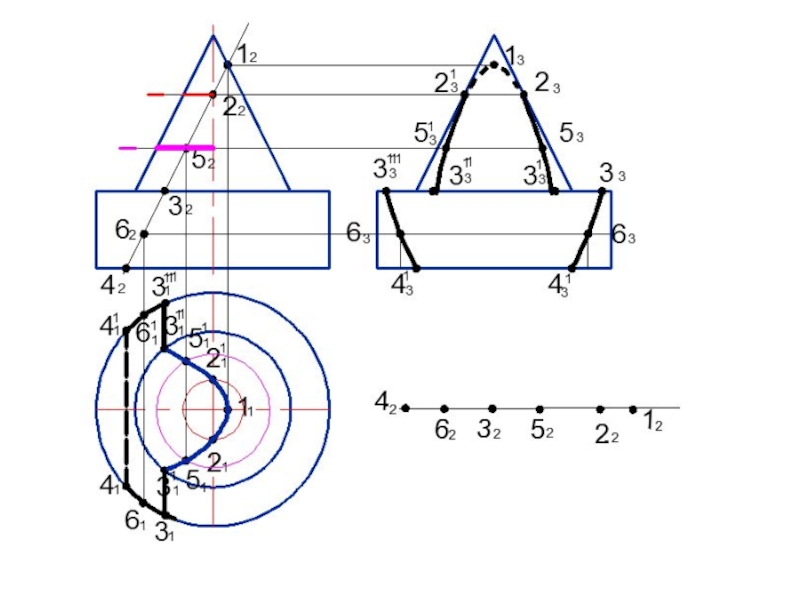
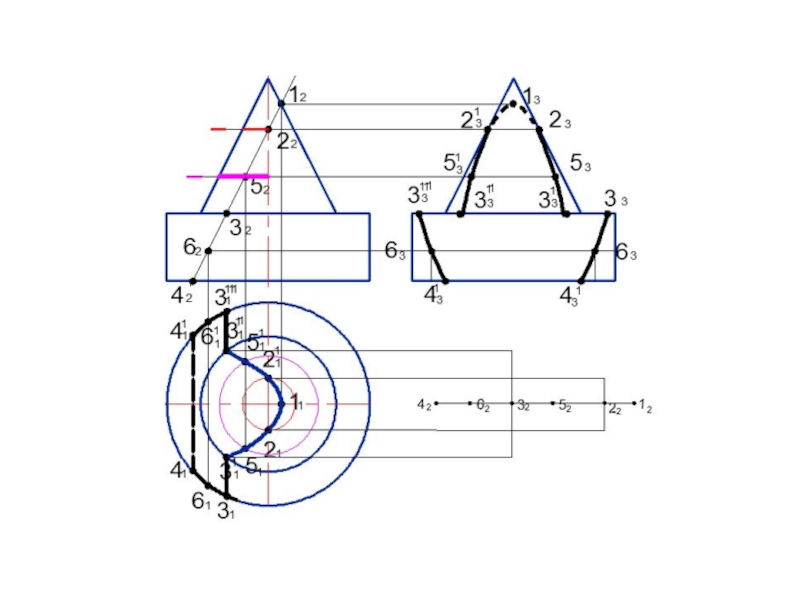
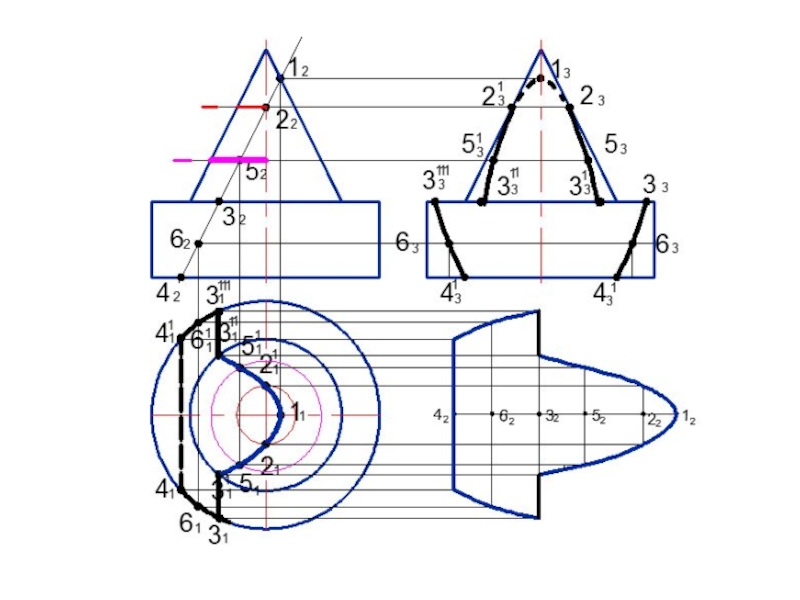
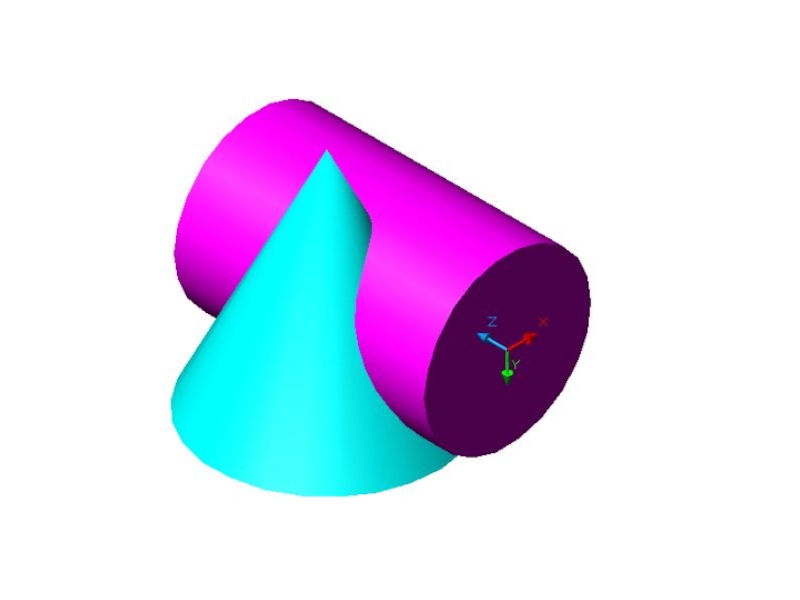
Слайд 54Задача.
Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей
Слайд 73ОСНОВНОЙ ПРИНЦИП
СФЕРА С ПОВЕРХНОСТЯМИ ВРАЩЕНИЯ, ОСИ КОТОРЫХ
ПРОХОДЯТ ЧЕРЕЗ ЦЕНТР СФЕРЫ, ПЕРЕСЕКАЕТСЯ ПО ОКРУЖНОСТЯМ, ПЛОСКОСТИ КОТОРЫХ ПЕРПЕНДИКУЛЯРНЫ
ОСИ ВРАЩЕНИЯ ПОВЕРХНОСТИ
Слайд 75СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР
1. ПЕРЕСЕКАЮТСЯ ПОВЕРХНОСТИ ВРАЩЕНИЯ
ОСИ ВРАЩЕНИЯ ПОВЕРХНОСТЕЙ
ПЕРЕСЕКАЮТСЯ
ПОВЕРХНОСТИ ИМЕЮТ ОБЩУЮ ПЛОСКОСТЬ
СИММЕТРИИ
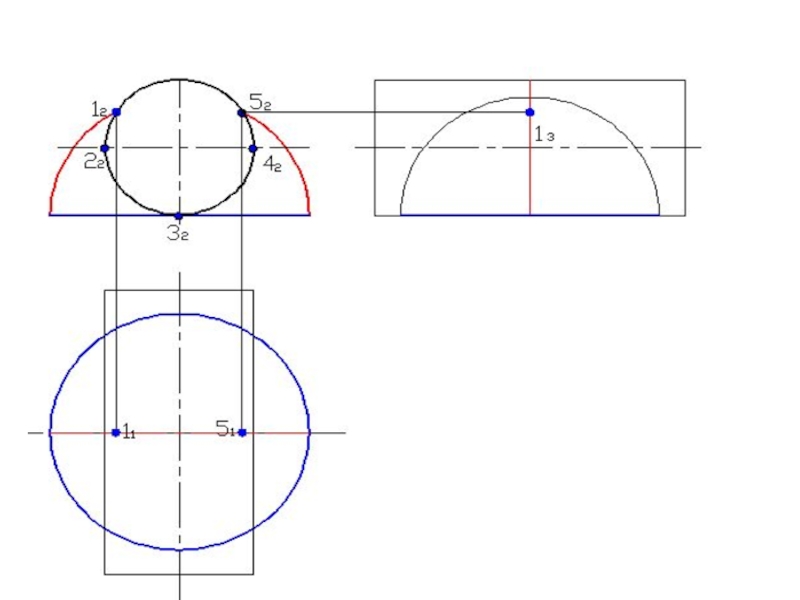
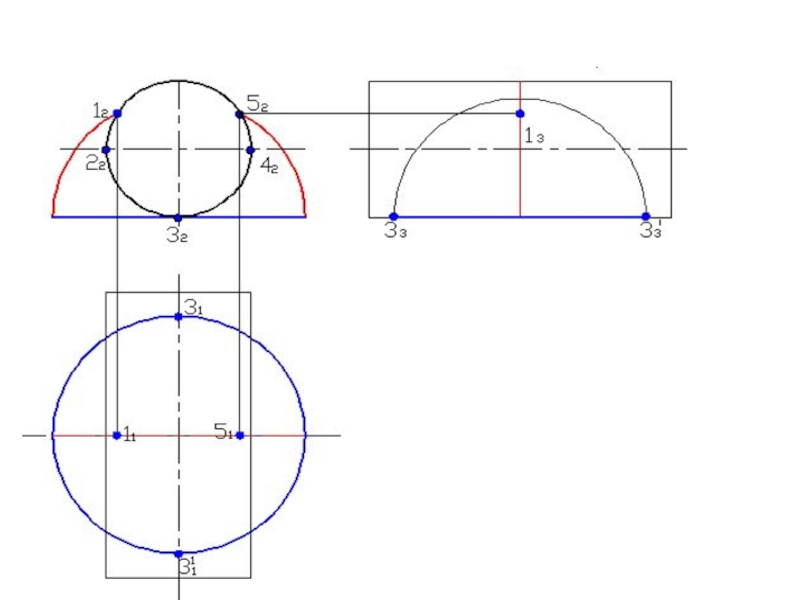
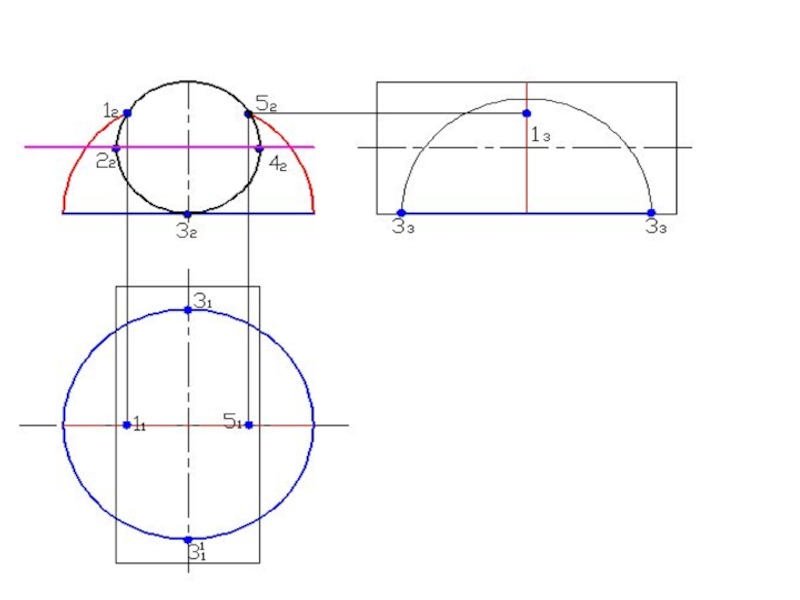
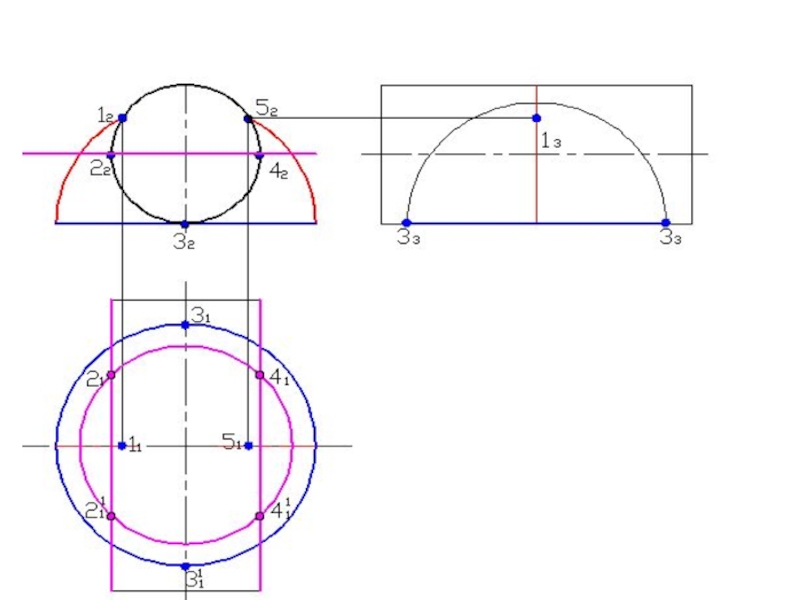
Слайд 76Построить линию пересечения поверхностей
А2
Минимальная сфера вписана в большую поверхность R
min
R min
32
12
22
Rmax
Слайд 80ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА ОПИСАННЫЕ ИЛИ ВПИСАННЫЕ В ДРУГУЮ ПОВЕРХНОСТЬ
2- го ПОРЯДКА, ПЕРЕСЕКАЮТСЯ ПО ДВУМ КРИВЫМ ВТОРОГО ПОРЯДКА, ПЛОСКОСТИ
КОТОРЫХ ПРОХОДЯТ ЧЕРЕЗ ПРЯМУЮ, СОЕДИНЯЮЩУЮ ТОЧКИ ПЕРЕСЕЧЕНИЯ ЛИНИЙ КАСАНИЯ
Слайд 87 РАЗВЕРТКА ПОВЕРХНОСТИ – ЭТО ПЛОСКАЯ ФИГУРА, КОТОРАЯ
ПОЛУЧАЕТСЯ СОВМЕЩЕНИЕМ ВСЕЙ БОКОВОЙ ПОВЕРХНОСТИ ОБЪЕКТА С
ПЛОСКОСТЬЮ
Слайд 891. ТОЧНЫЕ – ПОСТРОЕННЫЕ ГРАФОАНАЛИТИЧЕСКИМ СПОСОБОМ
2. ПРИБЛИЖЕННЫЕ – ВЫПОЛНЕННЫЕ СПОСОБОМ
АППРОКСИМАЦИИ РАЗВЕРТКИ РАЗВЕРТЫВАЕМЫХ ПОВЕРХНОСТЕЙ (ЦИЛИНДРЫ, КОНУСЫ)
3. УСЛОВНЫЕ – РАЗВЕРТКИ НЕРАЗВЕРТЫВАЕМЫХ ПОВЕРХНОСТЕЙ
(СФЕРА, ТОР)
Слайд 90СПОСОБЫ ПОСТРОЕНИЯ РАЗВЕРТОК ПОВЕРХНОСТЕЙ
АППРОКСИМАЦИЯ – ЗАМЕНА СЛОЖНОЙ ПОВЕРХНОСТИ
ПРОСТОЙ, ВПИСАННОЙ ИЛИ ОПИСАННОЙ МНОГОГРАННОЙ ПОВЕРХНОСТЬЮ
1. СПОСОБ НОРМАЛЬНОГО
СЕЧЕНИЯ2. СПОСОБ РАСКАТКИ
3. СПОСОБ ТРИАНГУЛЯЦИИ
Слайд 91АППРОКСИМАЦИЯ
В КРУГОВОЕ ОСНОВАНИЕ ВПИСЫВАЮТ ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК,
ЧЕРЕЗ ВЕРШИНЫ МНОГОУГОЛЬНИКА ПРОВОДЯТ РЕБРА ПРИЗМЫ ИЛИ ПИРАМИДЫ
Слайд 92Способ нормального сечения
Нормальное сечение - это сечение поверхности плоскостью перпендикулярной
оси вращения или высоте поверхности
Слайд 103Задача.
Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей
30
Слайд 105Цилиндр является фронтально проецирующей поверхностью, так как все его образующие
фронтально проецирующие прямые.
Линия пересечения заданных поверхностей на фронтальной плоскости совпадает
с очерком цилиндра
Слайд 118сечение цилиндра
эллипс
СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
bп21
12
121
11
1
2
211
221
21
22
21
32
3
31
311
312
31
411
42
41
412
41
4
51
5
521
52
bп2
