Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Устная работа
Содержание
- 1. Устная работа
- 2. Как найти радиус окружности, описанной около правильного
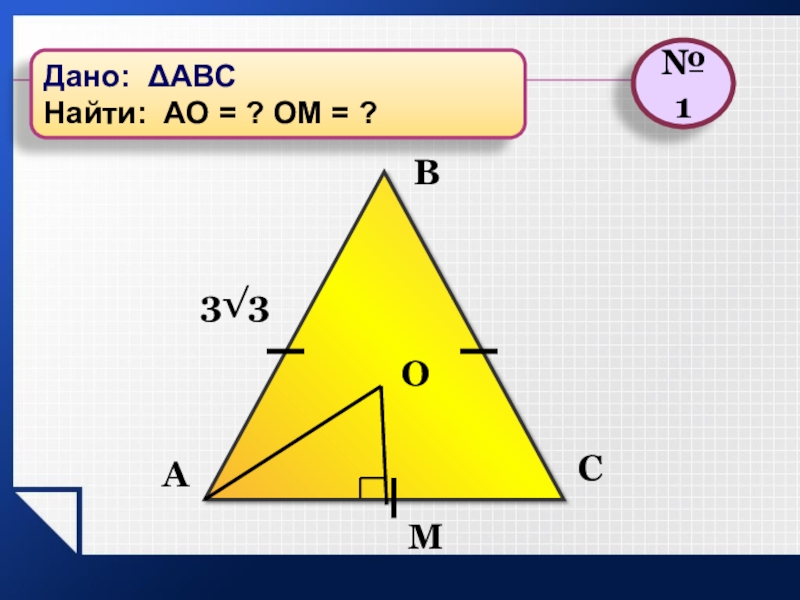
- 3. АВС3√3ОМ№1Дано: АВСНайти: АО = ? ОМ = ?
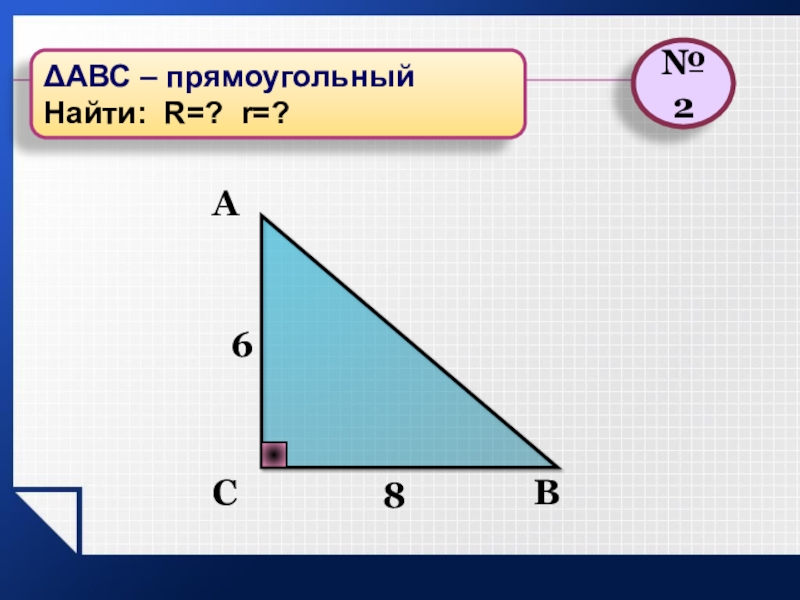
- 4. ВСА86№2АВС – прямоугольныйНайти: R=? r=?
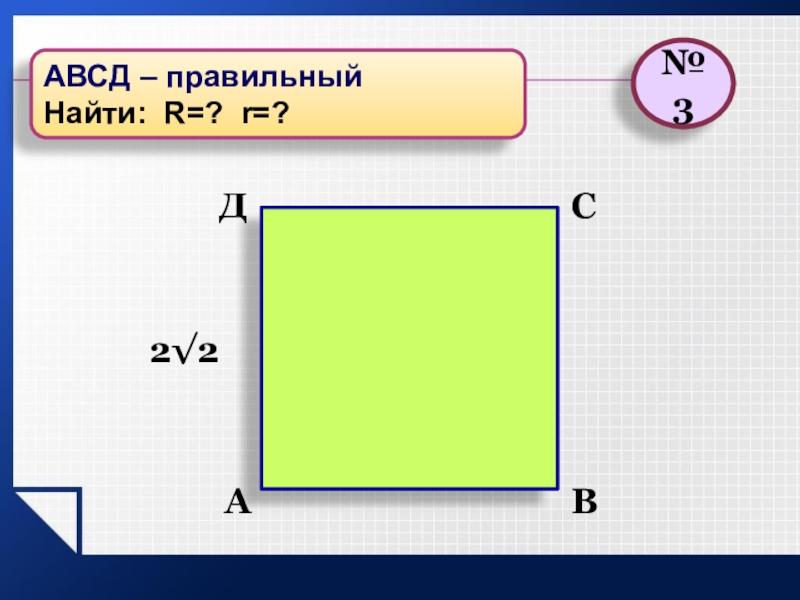
- 5. ВСА2√2№3АВСД – правильныйНайти: R=? r=? Д
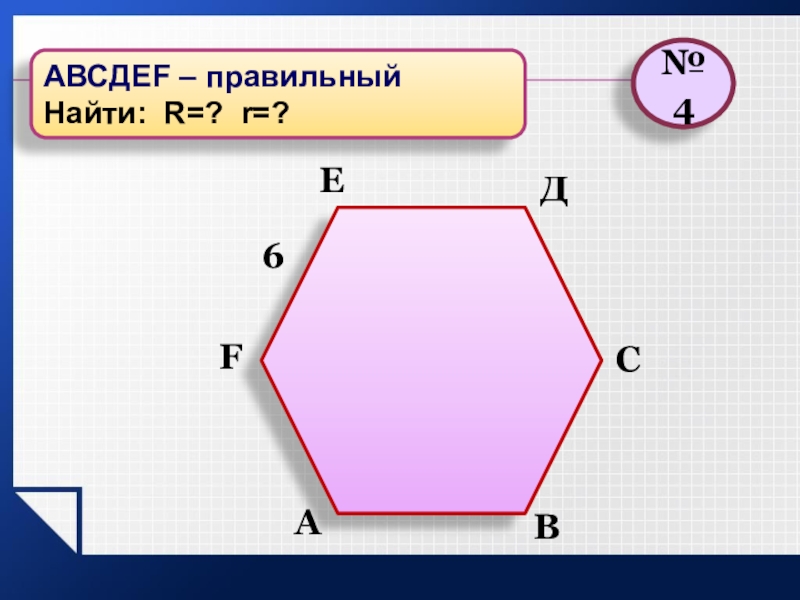
- 6. ВСА6№4АВСДЕF – правильныйНайти: R=? r=? ДЕF
- 7. Вписанная и описанная призмы.
- 8. Призма называется
- 9. Призма называется описанной около цилиндра, если ее
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Правильная четырехугольная призма описана
- 15. Слайд 15
- 16. В основании прямой призмы
- 17. В
- 18. Прямоугольный
- 19. Домашнее задание:
- 20. Скачать презентанцию
Как найти радиус окружности, описанной около правильного n-угольника?Как найти радиус окружности, вписанной в правильный n-угольник?
Слайды и текст этой презентации
Слайд 2Как найти радиус окружности, описанной около правильного
n-угольника?
Как найти радиус
окружности, вписанной в правильный
n-угольник?
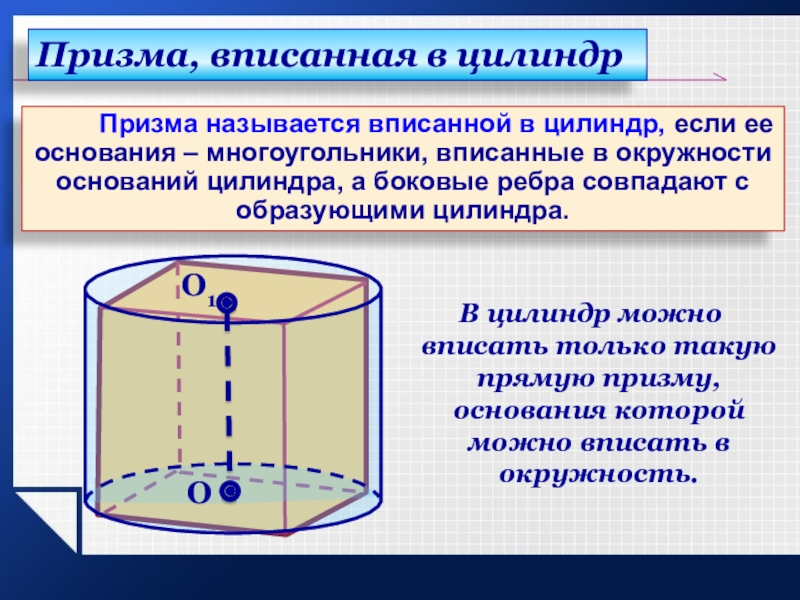
Слайд 8 Призма называется вписанной в цилиндр,
если ее основания – многоугольники, вписанные в окружности оснований цилиндра,
а боковые ребра совпадают с образующими цилиндра.Призма, вписанная в цилиндр
В цилиндр можно вписать только такую прямую призму, основания которой можно вписать в окружность.
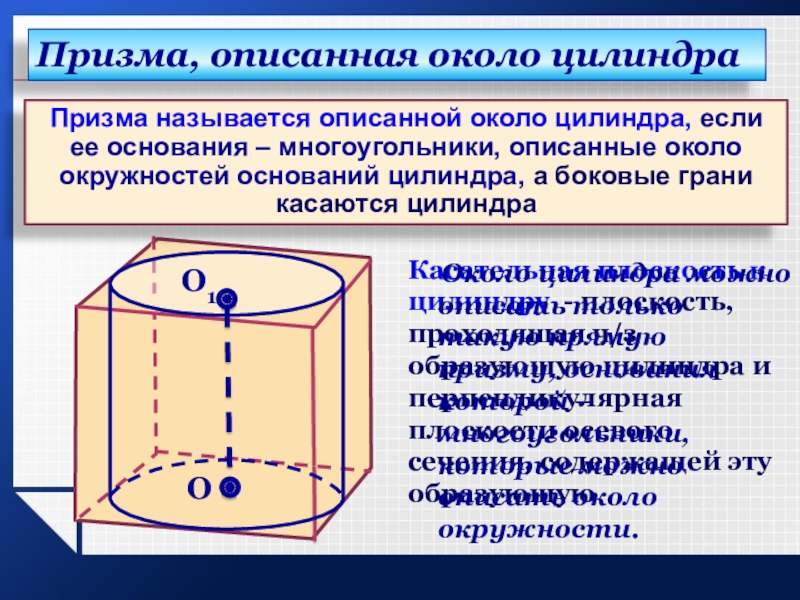
Слайд 9Призма называется описанной около цилиндра, если ее основания – многоугольники,
описанные около окружностей оснований цилиндра, а боковые грани касаются цилиндра
Касательная
плоскость к цилиндру - плоскость, проходящая ч/з образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующуюПризма, описанная около цилиндра
Около цилиндра можно описать только такую прямую призму, основания которой – многоугольники, которые можно описать около окружности.
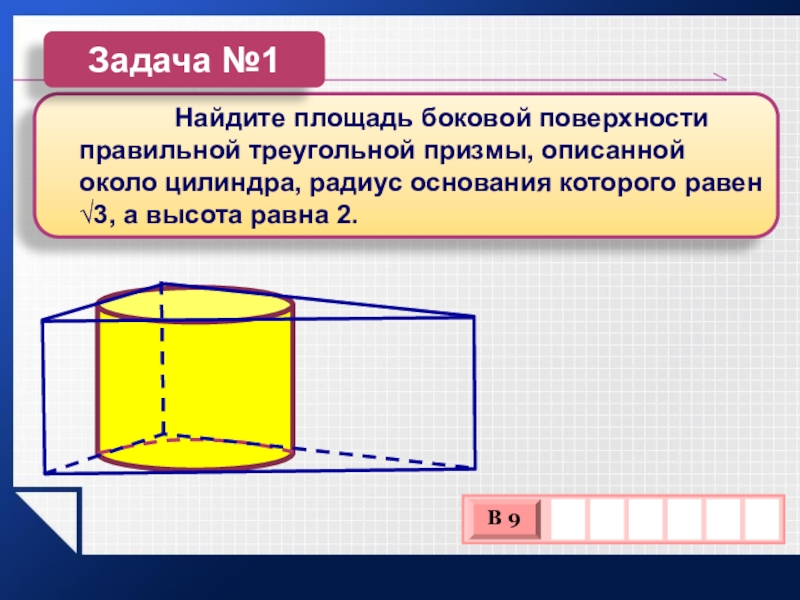
Слайд 10 Найдите
площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус
основания которого равен √3, а высота равна 2.Задача №1
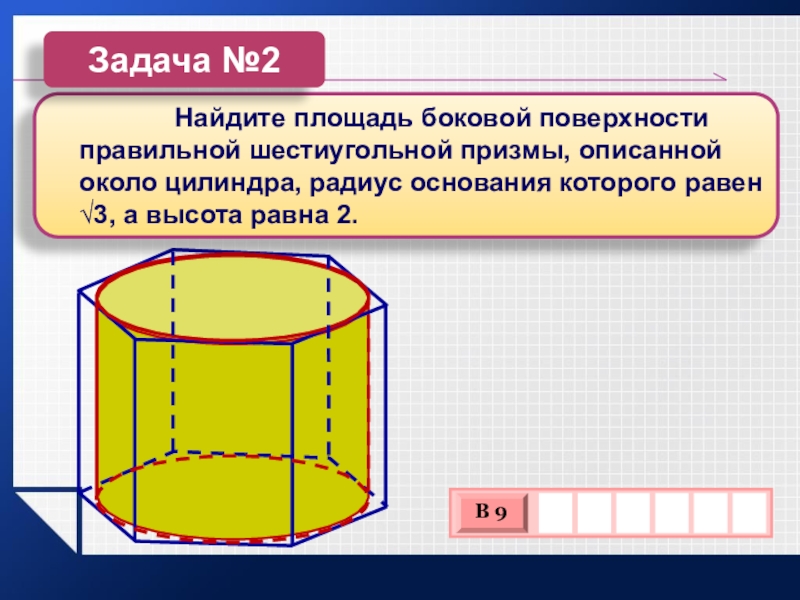
Слайд 11 Найдите
площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус
основания которого равен √3, а высота равна 2.Задача №2
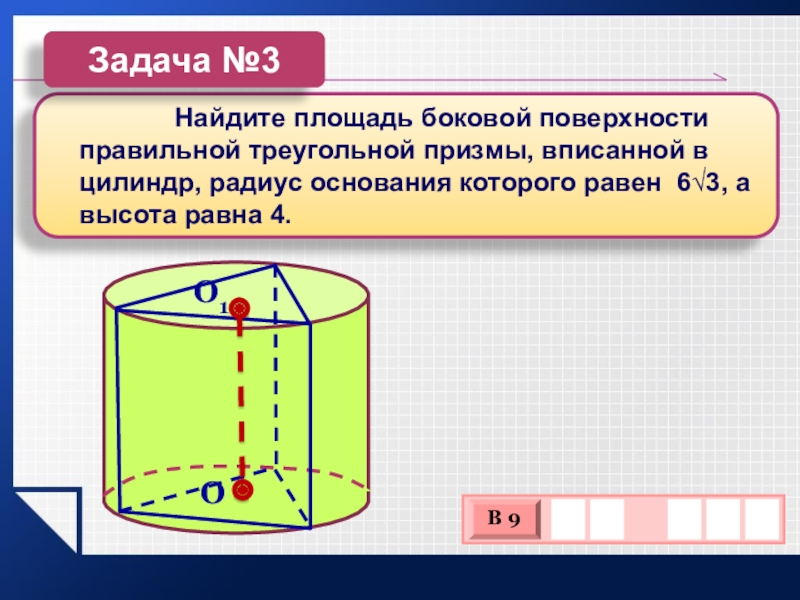
Слайд 12 Найдите
площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус
основания которого равен 6√3, а высота равна 4.Задача №3
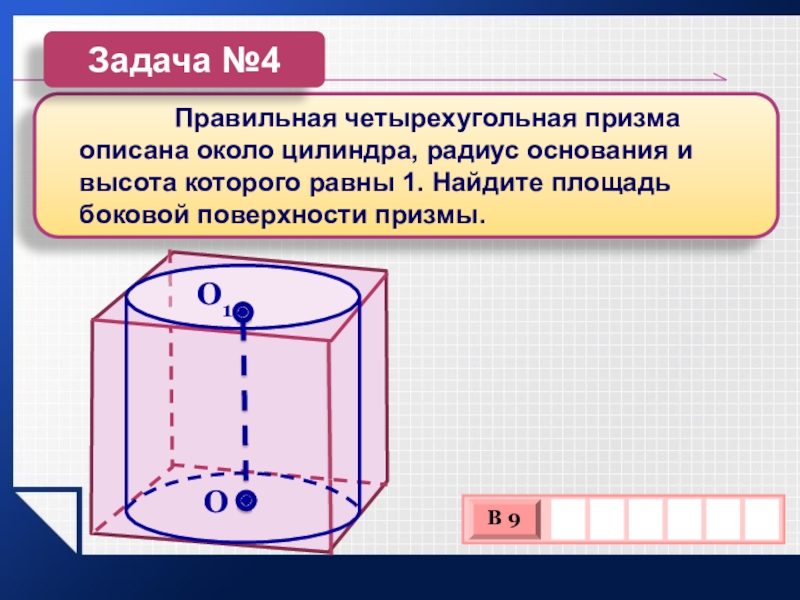
Слайд 13 Правильная
четырехугольная призма описана около цилиндра, радиус основания и высота которого
равны 1. Найдите площадь боковой поверхности призмы.Задача №4
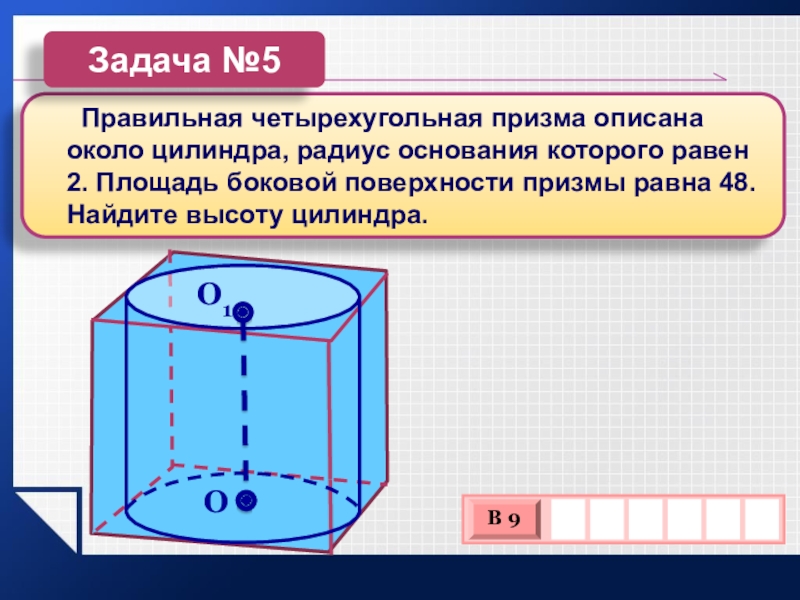
Слайд 14 Правильная четырехугольная призма описана около цилиндра, радиус
основания которого равен 2. Площадь боковой поверхности призмы равна 48.
Найдите высоту цилиндра.Задача №5
Слайд 15
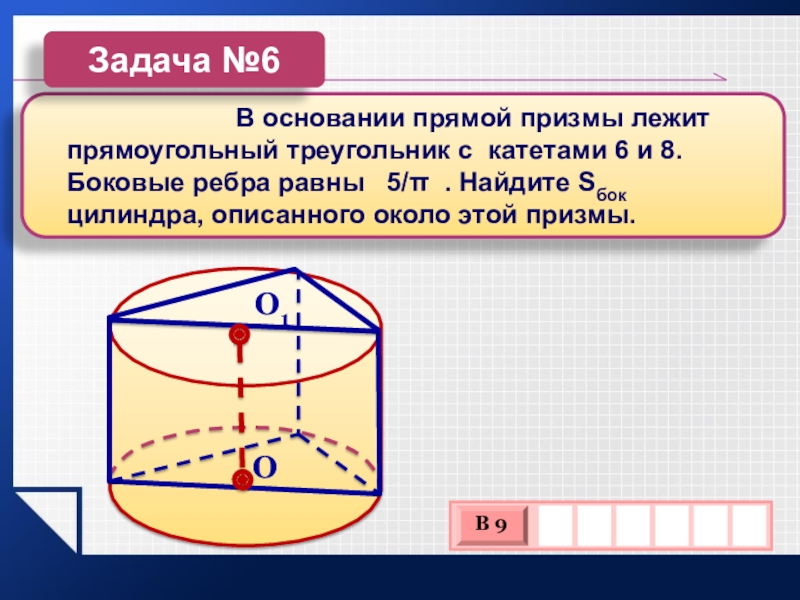
В основании прямой призмы лежит прямоугольный
треугольник с катетами 6 и 8. Боковые ребра равны 5/π . Найдите Sбок цилиндра, описанного около этой призмы.Задача №6
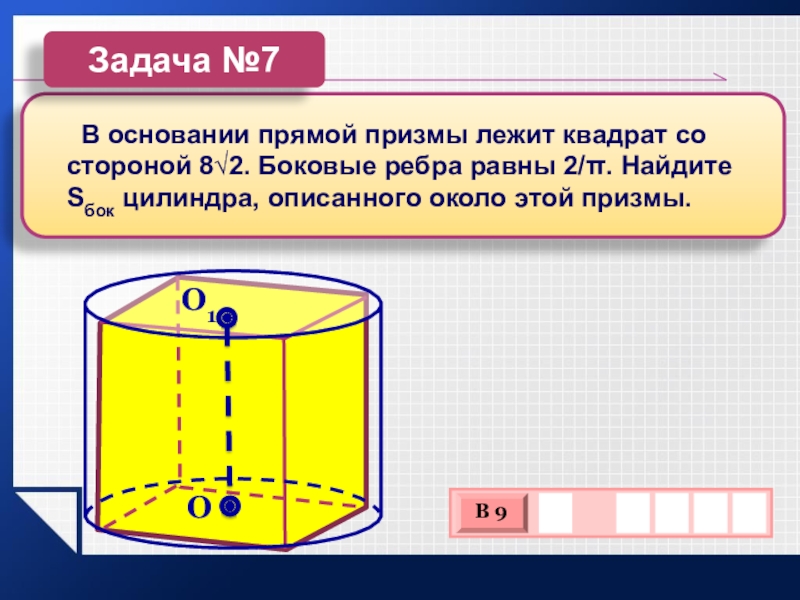
Слайд 16 В основании прямой призмы лежит квадрат со
стороной 8√2. Боковые ребра равны 2/π. Найдите Sбок цилиндра, описанного
около этой призмы.Задача №7
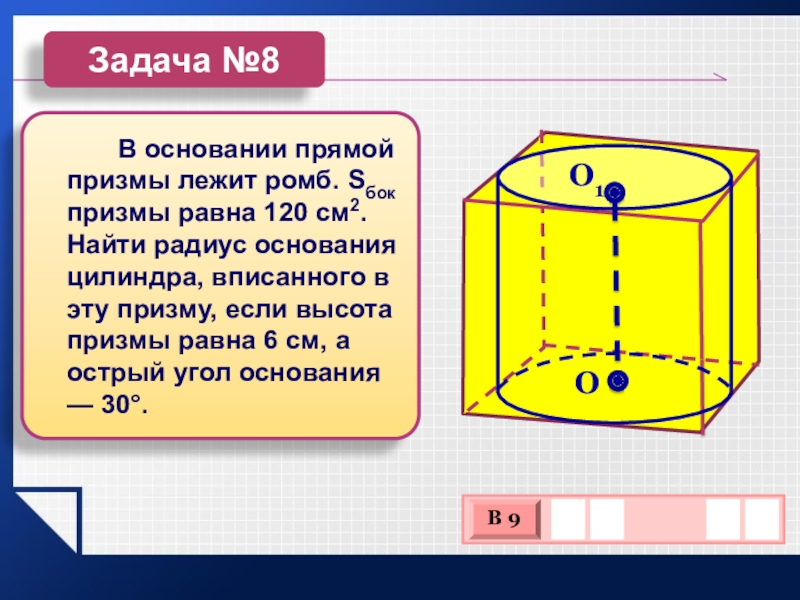
Слайд 17 В основании прямой призмы
лежит ромб. Sбок призмы равна 120 см2. Найти радиус основания
цилиндра, вписанного в эту призму, если высота призмы равна 6 см, а острый угол основания — 30°.Задача №8
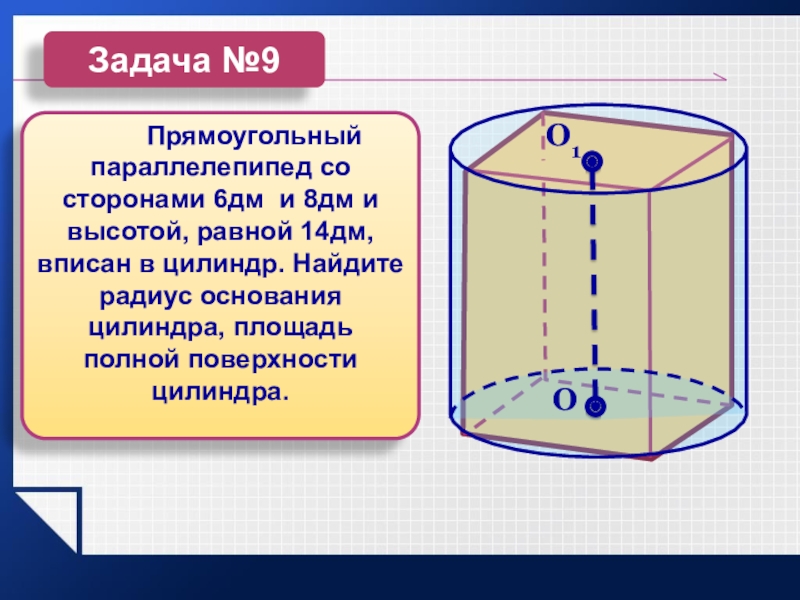
Слайд 18 Прямоугольный параллелепипед со сторонами
6дм и 8дм и высотой, равной 14дм, вписан в цилиндр.
Найдите радиус основания цилиндра, площадь полной поверхности цилиндра.Задача №9
