УСТОЙЧИВОСТЬ ПЛАЗМЫ

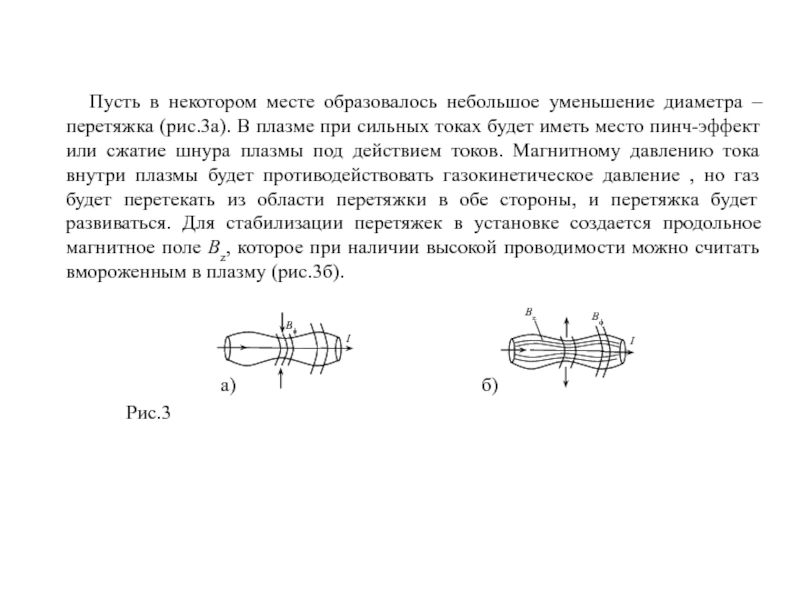
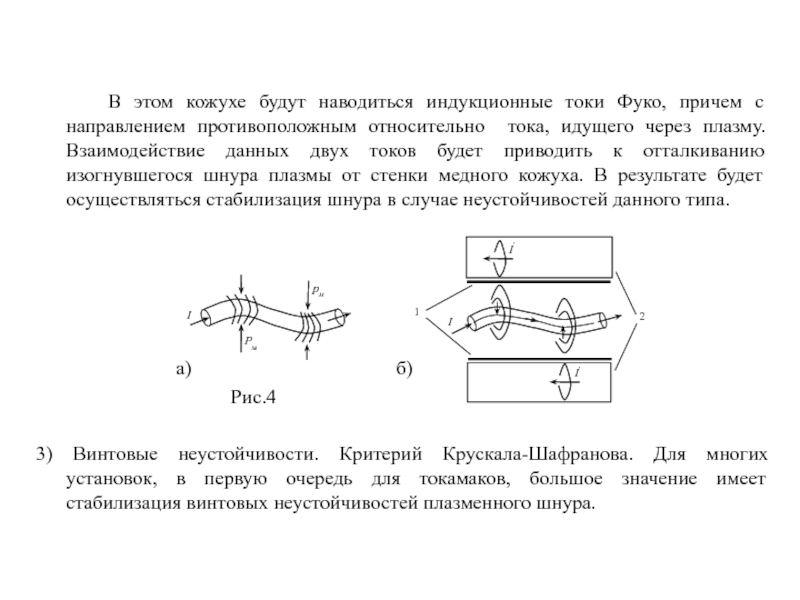
плазмы важны для установок содержащих низкотемпературную и высокотемпературную плазму, ввиду

того что потеря устойчивости может означать разрушение плазмы, исчезновение рабочих параметров и т.д. При проблеме управляемого термоядерного синтеза, ставящей своей целью нагрев плазмы до температур порядка Т=107-108 К, возник целый ряд неустойчивостей, препятствующих эффективному нагреву плазмы и вызывающих различные виды потери энергии и частиц плазмы. Основными видами неустойчивостей плазмы являются следующие: 1) магнитогидродинамические (желобковая, токовые), 2) кинетические (пучковая, конусная, дрейфово-конусная). Первый вид неустойчивостей связан с изменением формы плазмы, второй вид обусловлен отклонением ее распределения по скоростям частиц от равновесного распределения. Важной величиной для определения равновесия плазмы является параметр :

Лекция15 УСТОЙЧИВОСТЬ ПЛАЗМЫ

магнитного. В ряде установок по получению горячей плазмы внешняя граница

плазмы и вакуума испытывает воздействие этих давлений. Для устойчивости границы плазмы данный параметр должен принимать значения в диапазоне <1, т.е. магнитное давление, как правило, превосходит газокинетическое.
Рассмотрим магнитогидродинамические неустойчивости плазмы. Желобковая неустойчивость впервые была обнаружена в первых термоядерных установках – пробкотронах. В плазменных установках данного вида требовалось создать плазму цилиндрической конфигурации, расположенную в магнитном поле, направленном вдоль оси системы. Рассмотрим границу плазменного столба (рис.1). Пунктиром показаны контуры невозмущенной плазмы.

расположена тонкая магнитная трубка. В силу вмороженности силовых линий магнитного

поля при достаточно высокой проводимости, данная трубка может всплывать к поверхности плазмы под действием газокинетического давления.




Рис.1

Вблизи поверхности плазмы такая трубка может создать поверхность, напоминающую чередование желобков и выступов (рис.1). Теоретическое рассмотрение данного явления приводит к условию устойчивости границы в виде:

а варьирование производится вдоль радиуса. Неравенство означает, что для устойчивости

границы плазмы величина магнитного поля B должна возрастать при увеличении расстояния от оси установки.
Если на границе поверхности плазмы образуется выступ (рис.2), то могут произойти следующие явления. Поляризация зарядов приводит к появлению электрического поля E, направленного перпендикулярно к магнитному полю B. В скрещенных полях E и B начинается дрейф частиц обоих знаков вдоль радиуса. В результате размеры данных выступов будут увеличиваться за счет дрейфа.



Рис.2

плазмы в магнитных ловушках. Для стабилизации плазмы в установках данного

типа были созданы дополнительные магнитные поля, обеспечивающие рост суммарного магнитного поля при удалении от оси системы. При наличии данных полей происходит подавление неустойчивостей и граница плазмы становится стабильной.
Другой вид гидродинамических неустойчивостей – токовые возникают при прохождении через плазму значительных токов. В установках по получению термоядерной плазмы токи достигают диапазона I=104-106 A. Рассмотрим основные виды токовых неустойчивостей: “перетяжки”, “змейки” и “винтовые неустойчивости”.
1) “Перетяжки”. Предположим, что плазма имеет цилиндрическую форму и ток идет по оболочке плазмы.

диаметра – перетяжка (рис.3а). В плазме при сильных токах будет

иметь место пинч-эффект или сжатие шнура плазмы под действием токов. Магнитному давлению тока внутри плазмы будет противодействовать газокинетическое давление , но газ будет перетекать из области перетяжки в обе стороны, и перетяжка будет развиваться. Для стабилизации перетяжек в установке создается продольное магнитное поле Bz, которое при наличии высокой проводимости можно считать вмороженным в плазму (рис.3б).



а) б)
Рис.3

внешнего магнитного поля Bϕ будет противодействовать давление постоянного магнитного поля

Bz, которое будет стремиться вернуть первоначальную форму плазмы. В силу вмороженности силовые линии поля Bz не покинут плазму и обеспечат стабильность плазменного шнура от данных неустойчивостей.
2) “Змейки”. Другим видом токовых неустойчивостей являются так называемые “змейки” (рис.4). В результате развития данной неустойчивости шнур плазмы приобретает изгиб (рис.4а). С внутренней стороны изгиба шнура давление магнитного поля Bϕ будет больше, чем с наружной. Поэтому данная неустойчивость будет увеличиваться, не находя никакого противодействия. Для стабилизации неустойчивости вплотную к стенке камеры (1) располагается массивный медный кожух (2) (рис.4б).

Фуко, причем с направлением противоположным относительно тока, идущего через плазму.

Взаимодействие данных двух токов будет приводить к отталкиванию изогнувшегося шнура плазмы от стенки медного кожуха. В результате будет осуществляться стабилизация шнура в случае неустойчивостей данного типа.





а) б)
Рис.4

3) Винтовые неустойчивости. Критерий Крускала-Шафранова. Для многих установок, в первую очередь для токамаков, большое значение имеет стабилизация винтовых неустойчивостей плазменного шнура.

осевое (тороидальное) Bθ и поле тока Bϕ (рис.5). Результирующее магнитное

поле является спиралеобразным с шагом , где r –малый радиус тора. При наличии высокой проводимости плазмы и эффекте вмороженности силовых линий шнур плазмы может приобрести такую же спиральную конфигурацию, как и магнитное поле. Чтобы этого не произошло, шаг спирали h должен превышать длину установки L:

Подставим выражение для h в неравенство:




Выражение q(r) является запасом устойчивости относительно влияния винтовых неустойчивостей. Данный критерий имеет название Крускала-Шафранова в честь теоретиков впервые получивших данное выражение для плазмы токамаков.

Рис.5

Кинетические неустойчивости в плазме, как правило, связаны с отклонением функции распределения частиц по скоростям в плазме от равновесного максвелловского распределения. В качестве примера можно привести магнитную ловушку, в которой ввиду наличия конуса потерь, отсутствуют электроны в диапазоне малых поперечных энергий. На рис.6 изображена функция (2), которая соответствует распределению по поперечным энергиям, а пунктир (1) показывает вид функции в диапазоне низких энергий в условии равновесия. Распределение по энергиям (2) похоже на ситуацию с инверсной заселенностью энергетических уровней для лазерных сред.

Рис.6

Механизм возникновения неустойчивости в данном случае связан с нарастанием переменного электрического поля в электромагнитной волне, которая воздействует на заряженные частицы. Как следствие этого, происходит увеличение коэффициента диффузии относительно его классического значения:



В результате коэффициент диффузии становится пропорциональным квадрату электрического поля, и диффузия приобретает аномальный характер.