Слайд 1Вопрос 3. Корреляционно-регрессионный анализ
Слайд 2Примеры
Менеджер интересуется, зависит ли объем продаж в этом месяце от
объема рекламы в этом же периоде?
Преподаватель хочет выяснить, есть ли
зависимость между количеством часов, потраченных студентом на занятия, и результатами экзамена?
Врач исследует, влияет ли кофеин на сердечные болезни и существует ли связь между возрастом человека и его кровяным давлением?
Зоолог стремится узнать, есть ли связь между весом определенного животного при рождении и его продолжительностью жизни.
Социолог исследует, какова связь между уровнем преступности и уровнем безработицы в регионе? Есть ли зависимость между расходами на жилье и совокупным доходом семьи? Связаны ли доход от профессиональной деятельности и продолжительность образования?
Слайд 3Постановка проблемы
Наша цель – научиться отвечать на четыре вопроса:
Вопрос 1.
Существует ли связь между двумя или более переменными?
Вопрос 2. Какой
тип имеет эта связь?
Вопрос 3. Насколько она сильна?
Вопрос 4. Какой можно сделать прогноз, основываясь на этой связи?
Слайд 4Методы
Корреляция – статистический метод, позволяющий определить, существует ли зависимость между
переменными и на сколько она сильна.
Регрессия – статистический метод,
который используется для описания характера связи между переменными (положительная или отрицательная, линейная или нелинейная зависимость).
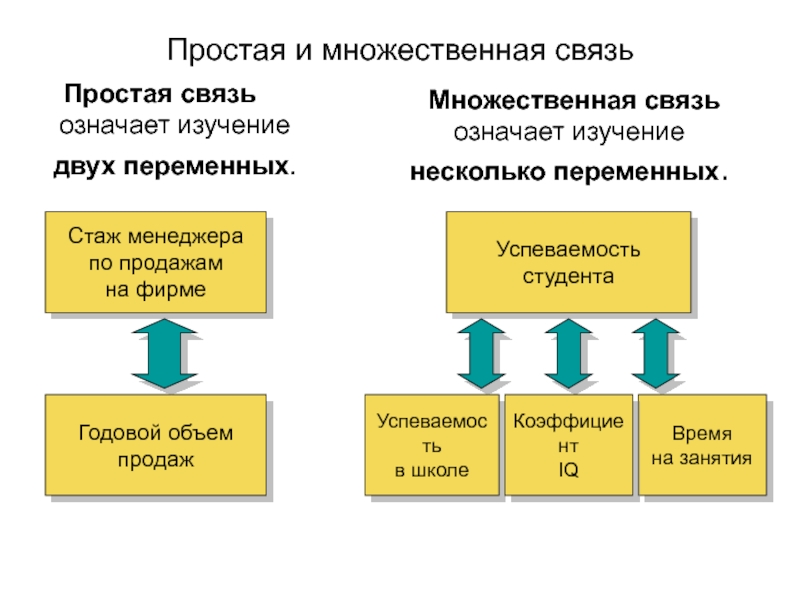
Слайд 5Простая и множественная связь
Множественная связь означает изучение несколько переменных.
Простая
связь означает изучение двух переменных.
Стаж менеджера
по продажам
на
фирме
Годовой объем
продаж
Успеваемость
студента
Успеваемость
в школе
Время
на занятия
Коэффициент
IQ
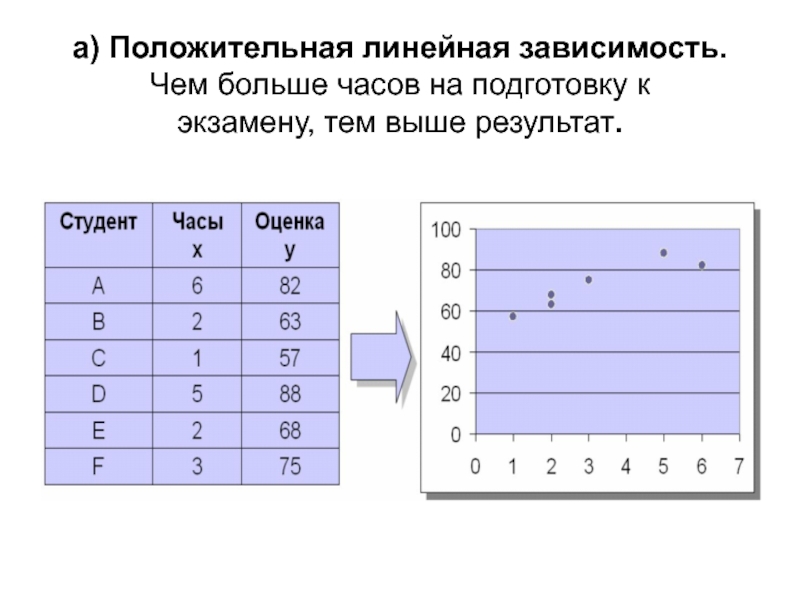
Слайд 6а) Положительная линейная зависимость. Чем больше часов на подготовку к
экзамену,
тем выше результат.
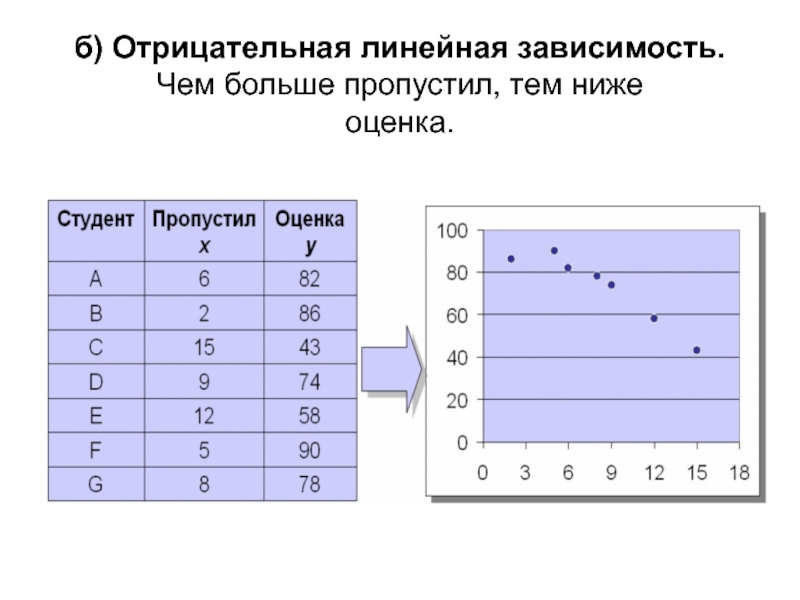
Слайд 7б) Отрицательная линейная зависимость. Чем больше пропустил, тем ниже
оценка.
Слайд 8в) Отсутствие зависимости.
Время подготовки не связано с количеством
вопросов, которые
задаст преподаватель.
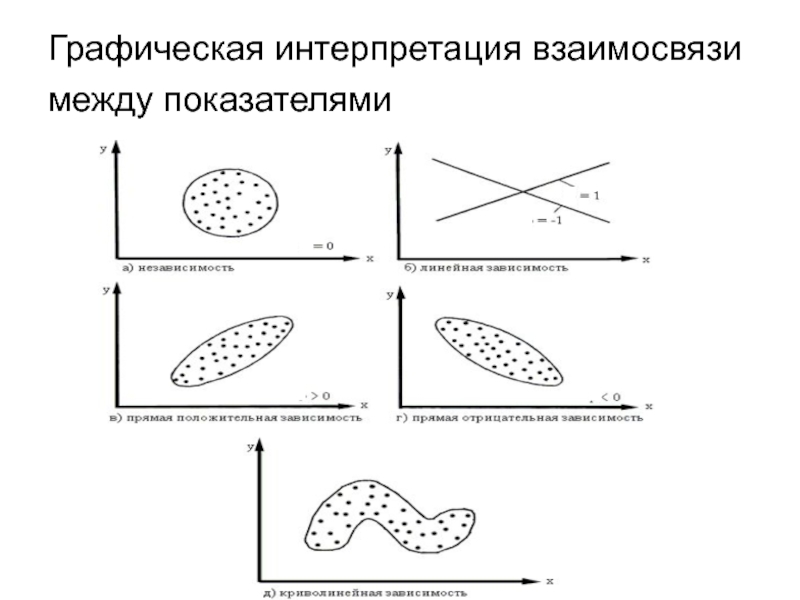
Слайд 9Графическая интерпретация взаимосвязи между показателями
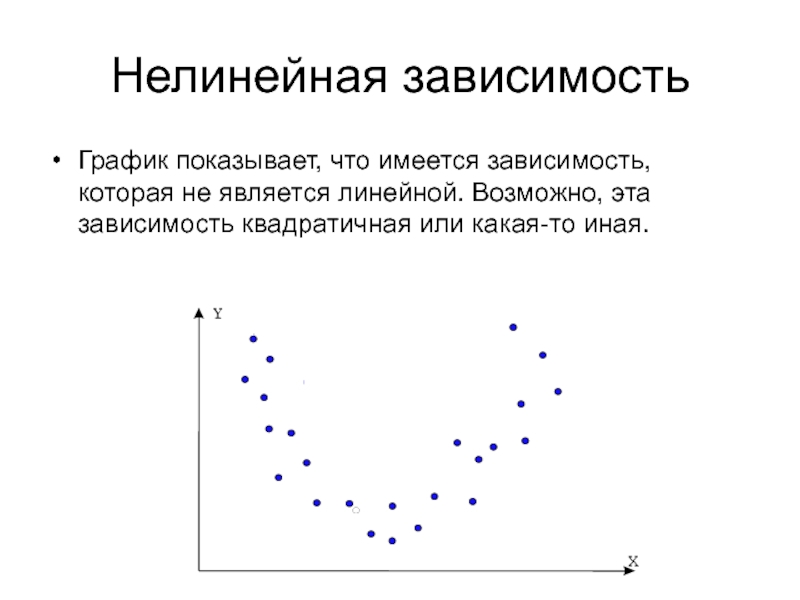
Слайд 10Нелинейная зависимость
График показывает, что имеется зависимость, которая не является линейной.
Возможно, эта зависимость квадратичная или какая-то иная.
Слайд 11Коэффициент корреляции измеряет силу и направление связи между двумя переменными.
Обозначения:
Выборочный коэффициент корреляции r
Коэффициент корреляции генеральной совокупности ρ
Слайд 12Значение коэффициента корреляции
Коэффициент корреляции изменяется на отрезке
от –1 до
+1.
Если между переменными существует сильная положительная связь, то значение
r будет
близко к +1.
Если между переменными существует сильная отрицательная связь, то значение r будет
близко к –1.
Когда между переменными нет линейной связи или она очень слабая, значение r будет близко к 0.
Слайд 14Критерии коэффициента корреляции
Слайд 16Постановка проблемы
Коэффициент корреляции генеральной совокупности ρ – это корреляция, вычисленная
с использованием всевозможных пар значений признаков (х,у) генеральной совокупности.
Требуется
Оценить
коэффициент корреляции генеральной совокупности ρ на основе значения коэффициента корреляции выборки r.
Условия
Выборочный коэффициент корреляции r используется для оценки ρ, если выполнены следующие предположения:
Переменные х и у линейно зависимы
Переменные являются случайными
Обе переменные имеют нормальное распределение
Слайд 17Последовательность действий
Чтобы принять верное решение, воспользуемся процедурой проверки гипотезы. Она
включает традиционные пять шагов:
Шаг 1. Сформулировать гипотезы.
Шаг 2. Построить критическую
область.
Шаг 3. Вычислить значение критерия.
Шаг 4. Сравнить, принять решение.
Шаг 5. Написать ответ.
Слайд 18Гипотезы
Гипотезы сформулированы следующим образом.
Основная гипотеза Н0: ρ = 0
Альтернативная гипотеза Н1:
ρ ≠ 0
Основная гипотеза утверждает, что не существует корреляции между
признаками х и у в генеральной совокупности. Альтернативная гипотеза утверждает, что корреляция между признаками х и у в генеральной совокупности значима.
Слайд 19Статистика и критическая область
Для проверки гипотезы используется t-критерий с
df
= n – 2 степенями свободы:
Границы двусторонней критической области находятся
при помощи таблиц (ПО) значений t-распределения.
Слайд 20Пять видов связи между переменными
1. Прямая причинно-следственная связь между переменными
(х определяет у). Наличие воды ускоряет рост растений, яд вызывает
смерть, жара – таяние льда.
2. Обратная причинно-следственная связь между переменными
(у определяет х). Исследователь может думать, что чрезмерное потребление кофе вызывает нервозность. Но, может быть, очень нервный человек хочет кофе, чтобы успокоить свои нервы?
3. Связь между переменными вызвана третьей переменной. Исследователь установил, что существует некая зависимость между числом утонувших людей и числом выпитых безалкогольных напитков в летнее время. Может быть, обе переменные связаны с жарой и потребностью во влаге?
4. Взаимосвязь между несколькими переменными. Исследователь может обнаружить значимую связь между оценками студентов в университете и оценками в школе. Но, возможно, действуют и другие переменные: IQ, количество часов занятий, влияние родителей, мотивация, возраст, авторитет преподавателей.
5. Зависимость случайна. Исследователь может найти значимую зависимость между увеличением количества людей, которые занимаются спортом и увеличением количества людей, которые совершают преступления. Но здравый смысл говорит, что любая связь между этими двумя переменными должна быть случайной.

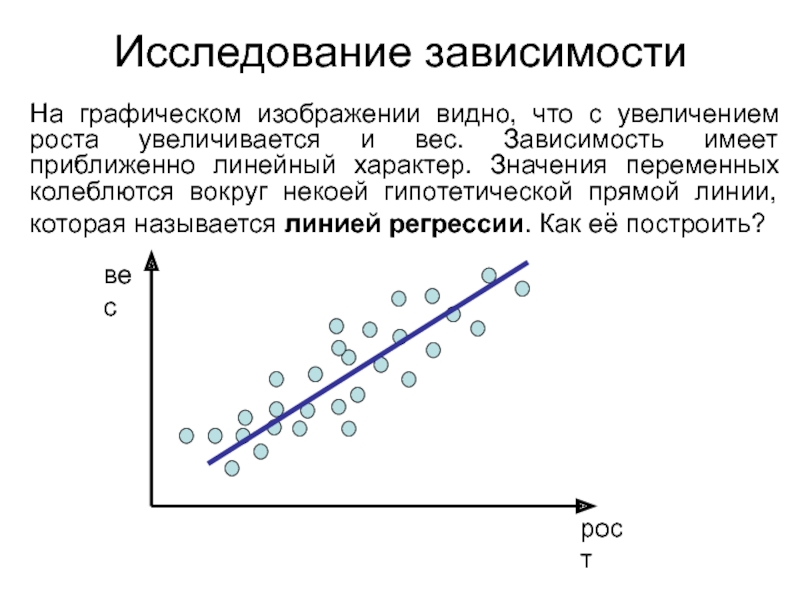
Слайд 21Исследование зависимости
На графическом изображении видно, что с увеличением роста увеличивается
и вес. Зависимость имеет приближенно линейный характер. Значения переменных колеблются
вокруг некоей гипотетической прямой линии, которая называется линией регрессии. Как её построить?
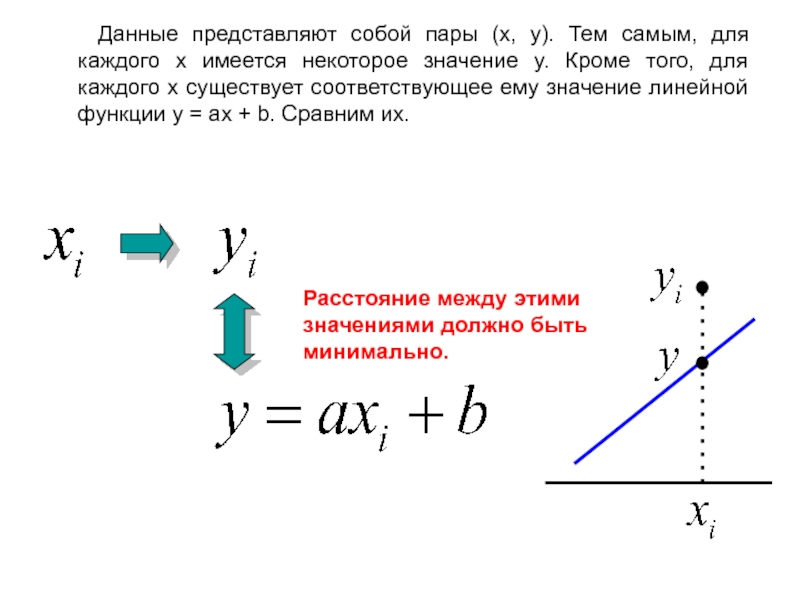
Слайд 22 Данные представляют собой пары (x, y). Тем самым,
для каждого x имеется некоторое значение y. Кроме того, для
каждого x существует соответствующее ему значение линейной функции y = ax + b. Сравним их.
Расстояние между этими значениями должно быть минимально.
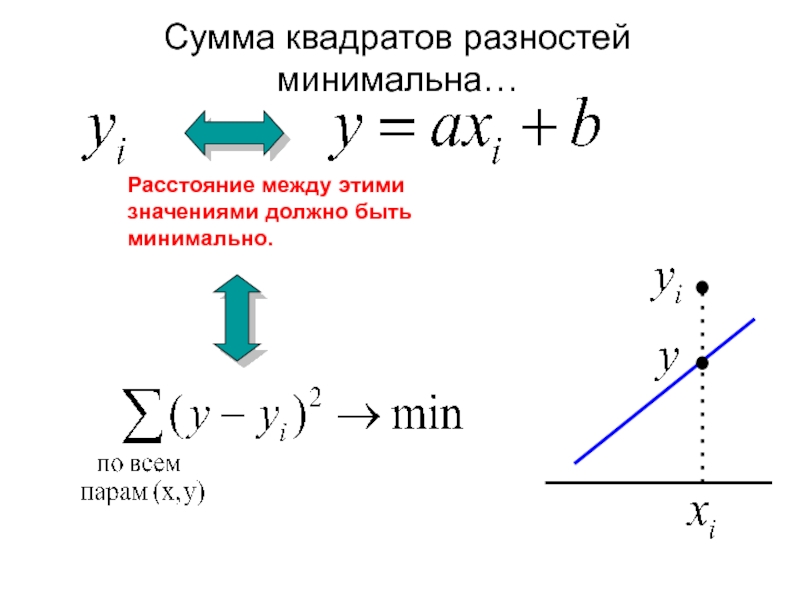
Слайд 23Сумма квадратов разностей минимальна…
Расстояние между этими значениями должно быть минимально.
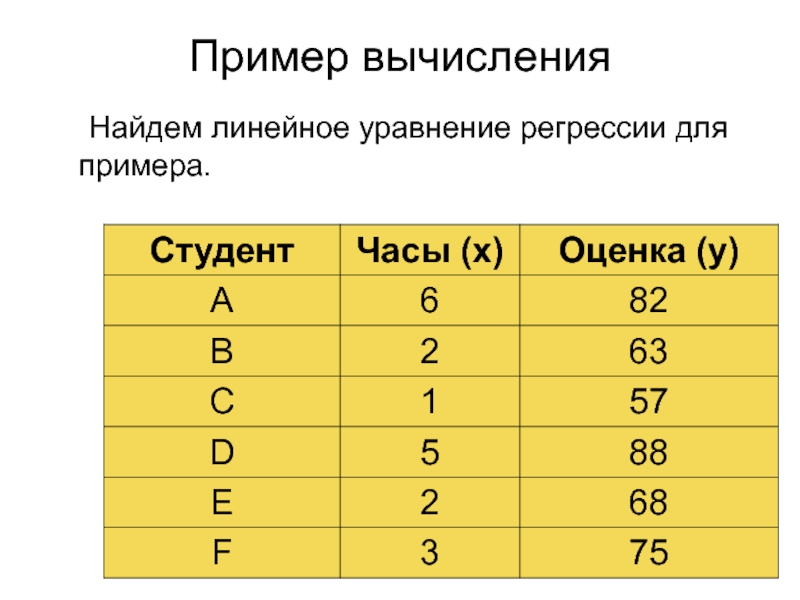
Слайд 24Пример вычисления
Найдем линейное уравнение регрессии для примера.
Слайд 25Ответ. Получили уравнение «наилучшей прямой»:
y = 5,6 x +
54,5
Слайд 26Интерпретация
1. Увеличение времени подготовки на 1 час приводит к
улучшению результата на 5,6 балла.
2. Чтобы улучшить результат на 10
баллов, нужно заниматься на 1,8 часа больше.
3. Если не заниматься вообще – получишь 54,5 балла.
4. Чтобы получить 100 баллов, нужно заниматься 8,1 часов.
Слайд 27Регрессионное исследование
Уже научились:
Шаг 1. Графически изобразить пары значений (x, y).
Шаг
2. Если визуально просматривается связь, найти коэффициент корреляции.
Шаг 3. Оценить
значимость коэффициента корреляции.
Шаг 4. Если коэффициент значим, то найти уравнение регрессии.
Шаг 5. Построить разумные прогнозы: для значения независимой переменной х предсказать значение зависимой переменной у.
Научимся:
Шаг 6. Оценить надежность прогноза: найти коэффициент детерминации, стандартную ошибку оценки и интервал предсказания.
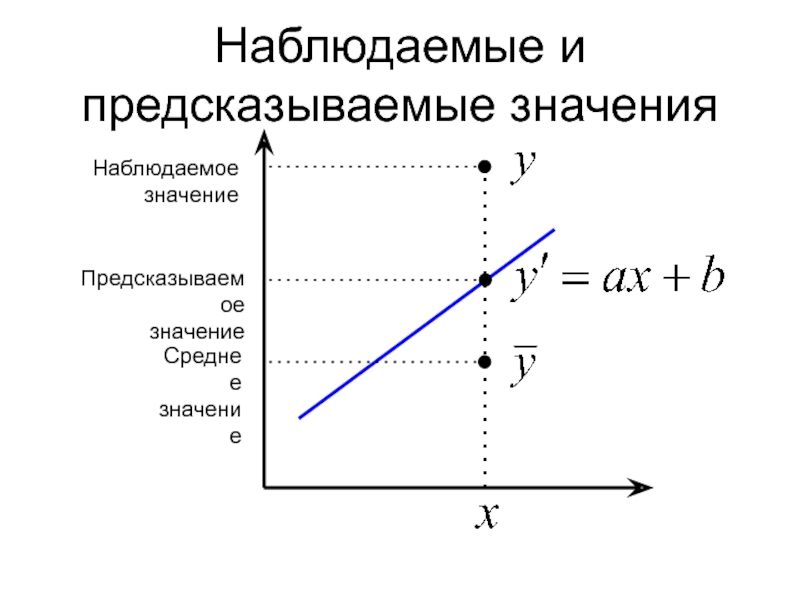
Слайд 28Наблюдаемые и предсказываемые значения
Наблюдаемое
значение
Предсказываемое
значение
Среднее
значение
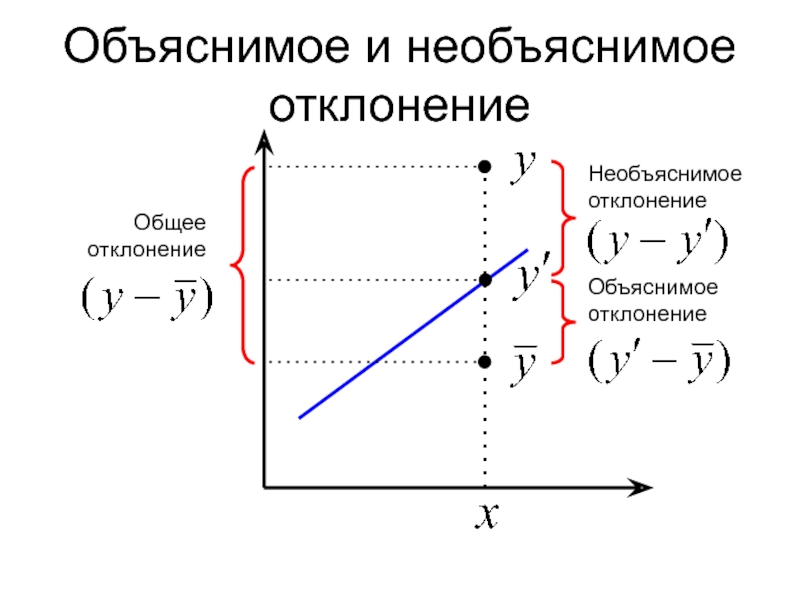
Слайд 29Объяснимое и необъяснимое отклонение
Необъяснимое отклонение
Объяснимое отклонение
Общее отклонение
Слайд 30Вариация в регрессионной модели
Общее отклонение есть сумма объяснимой и необъяснимой
вариации:
Общая
вариация
Объяснимая
вариация
Необъяснимая
вариация
Слайд 31Коэффициент детерминации
Коэффициент детерминации вычисляется как отношение объяснимой вариации к общей
вариации:
Коэффициент детерминации – это мера вариации зависимой переменной, которая определяется
линией регрессии и независимой переменной. Коэффициент обозначается r2.
Слайд 32Интерпретация коэффициента детерминации
Значение коэффициента детерминации можно получить, если возвести в
квадрат коэффициент корреляции.
Если r = 0,922, то r2 =
0,85 или 85%. Это означает, что 85% вариации зависимой переменной определяется вариацией независимой переменной.
Оставшиеся 15% – необъяснимая или случайная вариация. Это значение называется коэффициентом недетерминации и находится вычитанием коэффициента детерминации из единицы.
Слайд 33Стандартная ошибка оценки
Стандартная ошибка оценки – это стандартное отклонение наблюдаемых
значений у от предсказываемых значений у’:
Чем ближе наблюдаемые значения к
предсказываемым, тем меньше стандартная ошибка оценки.
Слайд 34Интервал предсказания
Выбрав значение α, получаем интервал, который с вероятностью (1
– α) содержит реальное значение у.
Слайд 35Пример
Сколько баллов получит студент, занимавшийся 4 часа?
Решение.
Шаг 1. Провели
необходимые вычисления
Шаг 2. Нашли у = 5,6·4 + 54,5 =
76,9
Шаг 3. Нашли стандартную оценку ошибки sest =5,08
Шаг 4. Нашли t-значение =0,95 и df = 6 – 2 = 4. Получили t=2,776
Шаг 5. Нашли E:
Слайд 36 Шаг 6. Подставили в формулу интервала:
Ответ. Прогнозируемое значение баллов, которое
может получить студент при 4 часах подготовки, находится с вероятностью
95% в интервале: