Второе начало термодинамики Второй закон термодинамики непосредственно связан с

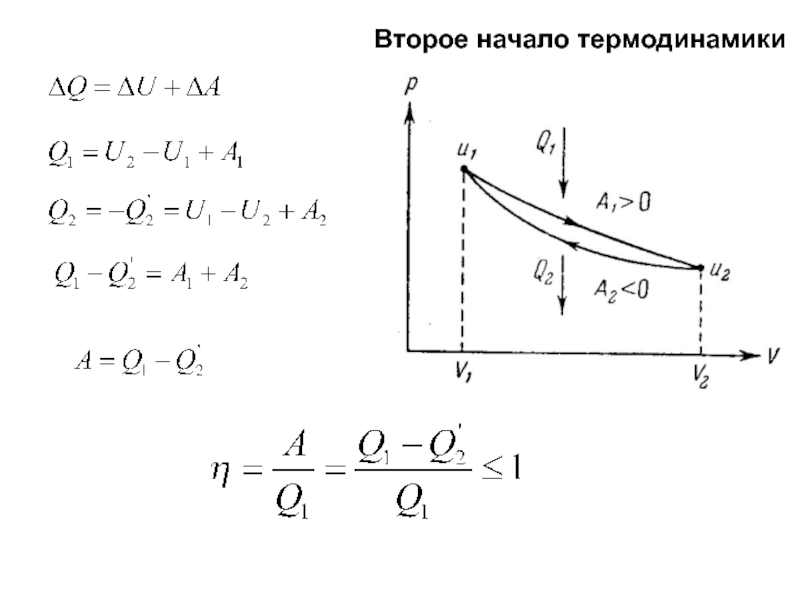
тепловых процессов. Энергия теплового движения молекул качественно отличается от всех

других видов энергии – механической, электрической, химической и т. д. Энергия любого вида, кроме энергии теплового движения молекул, может полностью превратиться в любой другой вид энергии, в том числе и в энергию теплового движения. Последняя может испытать превращение в любой другой вид энергии лишь частично. Поэтому любой физический процесс, в котором происходит превращение какого-либо вида энергии в энергию теплового движения молекул, является необратимым процессом, т. е. он не может быть осуществлен полностью в обратном направлении.

Первое начало термодинамики – это обобщение закона сохранения энергии на тепловые процессы.

Оказывается, однако, что не все процессы разрешённые первым началом термодинамики возможны. Второе начало термодинамики формулирует эти ограничения.

КПД η=1, или невозможен вечный двигатель 2-го рода.

в работу всё тепло, извлекаемое из окружающих тел.
Если бы

тепловой двигатель с КПД =1 был возможен, т.е. если бы всё тепло могло превращаться в работу (Q2=0), мы не нуждались бы в более холодных телах и могли бы совершать работу за счёт отбора тепла из окружающих нас тел, например, от океана. В силу практической безграничности такого источника тепловой энергии это был бы вечный двигатель (второго рода).

Второе начало термодинамики

характеристикой необратимости процессов.
Понятие энтропии играет важную роль не только в

физике, но и в теории информации.

Рудольф Клаузиус
1822-1888

           ,

Можно доказать,. что энтропия (или «приведённое тепло») является функцией состояния (несмотря на то что количество теплоты функцией состояния не является.

Энтропия вводится через её изменение (как часто делается в физике). В дифференциальной форме

Изменение энтропии при переходе системы из состояния 1 в состояние 2 в равновесном процессе

S2 – S1 не зависит от вида процесса. S2 – S1 определяется лишь начальным и конечным состояниями.

только разность энтропий для разных состояний системы, но не саму

величину энтропии.

Энтропия определяется с точностью до постоянной.

Однако, используя третье начало термодинамики (теорема Нернста), согласно которому энтропия любой системы при температуре абсолютного нуля равна 0, можно найти и величину самой энтропии.

Второе начало термодинамики

Энтропия

уменьшается – она либо возрастает, либо остаётся постоянной.
В замкнутых системах:
Ещё

одна формулировка 2-го начала

В случае обратимых процессов энтропия замкнутой макросистемы не меняется

В случае необратимых процессов энтропия замкнутой макросистемы возрастает

Таким образом, величина возрастания энтропии в замкнутой системе может служить мерой необратимости процессов, протекающих в системе.

Анализ изменения энтропии даёт указание, в каком направлении могут происходить самопроизвольные необратимые процессы в замкнутой системе: в сторону возрастания энтропии.

теплоизолированных сосуда разделённых перегородкой с вентилем.
Равновесное состояние 1. В

сосуде 1 находится 1 моль идеального газа. В сосуде 2 – вакуум.

После того как вентиль открыли газ адиабатически расширился и заполнил объём 2. После того как давление и температура уравнялась образовалось равновесное состояние 2.

Переход очевидно необратимый. Должно быть S2-S1>0. Проверим.

Энтропия функция состояния. S2-S1 не зависит от пути перехода. Поэтому выберем такой путь на котором легче найти S2-S1.

Поскольку переход был адиабатический и работа не совершалась внутренняя энергия газа не изменилась, следовательно температура в равновесных состояниях 1 и 2 одна и та же.

процесс (энтропия – функция состояния).
Обратный процесс невозможен
В случае

изотермического процесса

началу (в замкнутых системах

) расширение газа в замкнутой системе – необратимый процесс.

Самопроизвольно он может протекать лишь в одну сторону.

Обратный процесс (самопроизвольное сжатие) запрещён вторым началом (поскольку энтропия при этом снижается).

Таким образом, анализ изменения энтропии указывает, какие неравновесные процессы в замкнутой системе возможны (протекают самопроизвольно), а какие нет.