Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Инверсия
Содержание
- 1. Инверсия
- 2. СодержаниеВведениеОпределение и свойства инвертных точек. Метод инверсии.
- 3. 1.Введение
- 4. Инверсия - изменение нормального положения компонентов, расположение
- 5. Цель работы: Изучить метод инверсии и его применение
- 6. Задачи: Знакомство с методом инверсии.Рассмотрение инверсии относительно
- 7. Достоинства способа:он помогает приобрести навык построения графиков
- 8. 2. Определение и свойства инвертных точек.Точка В
- 9. Преобразование плоскости, при котором каждая точка переходит
- 10. 3. Метод инверсии. 3.1. Инверсия относительно оси ОХ.Рассмотрим инверсию относительно оси ОХ.
- 11. (х
- 12. Свойства инверсии относительно оси Ох1. Если f(x)>0, то >0. Если f(x)
- 13. 4.Если f( -x)= f(x), то g(-
- 14. 7.Наибольшее значение функции изменяется и становится наименьшим,
- 15. 3.2. Построение графиков y=1/f(x).
- 16. у =
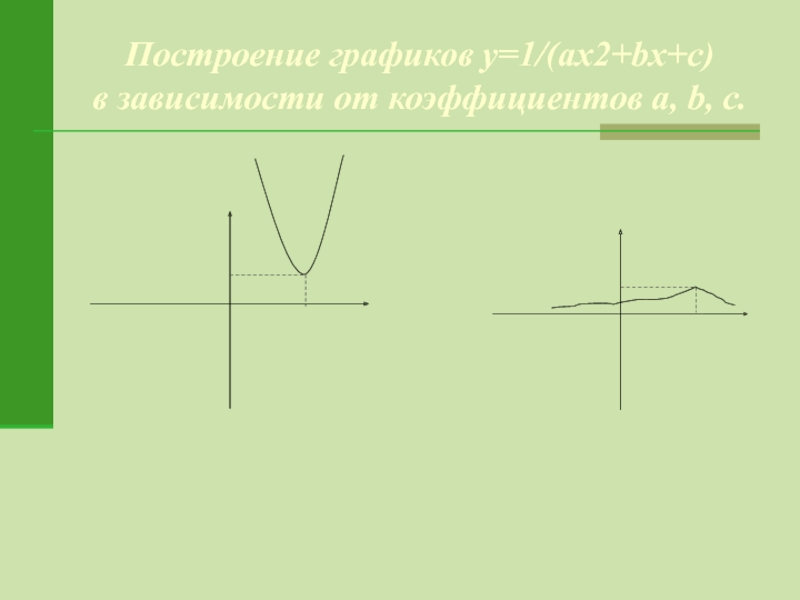
- 17. Построение графиков y=1/(ax2+bx+c) в зависимости от коэффициентов a, b, c.
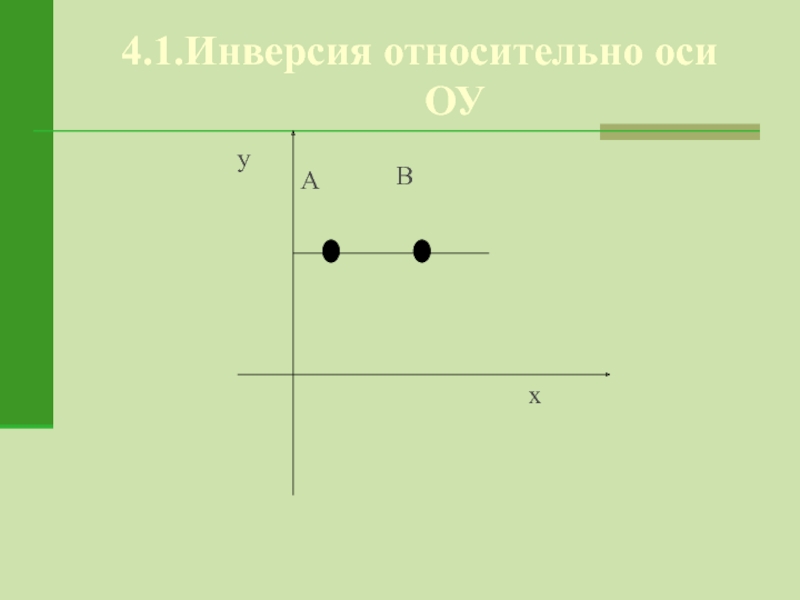
- 18. 4.1.Инверсия относительно оси ОУ
- 19. График функции g(x)=f( ) получается из
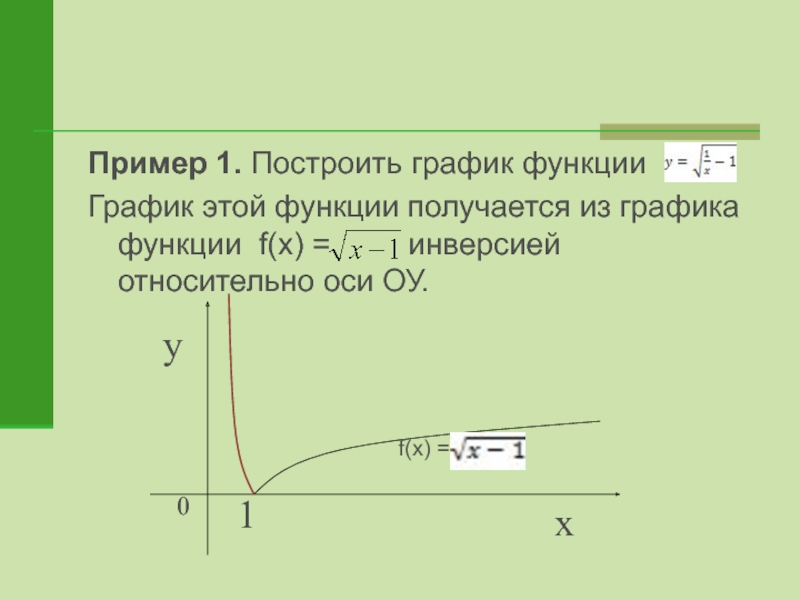
- 20. Пример 1. Построить график функции График этой
- 21. 5. Применение инверсии
- 22. С помощью графика установить:а) при каких значениях
- 23. Список используемой литературыА.П. Карп «Даю уроки математики»
- 24. СПАСИБО ЗА ВНИМАНИЕ!
- 25. Скачать презентанцию
СодержаниеВведениеОпределение и свойства инвертных точек. Метод инверсии. 3.1. Инверсия относительно оси ОХ. 3.2. Построение графиков y=1/f(x). 3.3. Построение графиков y=
Слайды и текст этой презентации
Слайд 1Муниципальное общеобразовательное учреждение
«Лермонтовская средняя общеобразовательная школа»
Тема: «Инверсия»
научно – исследовательская
работа
НиколаевнаСлайд 2Содержание
Введение
Определение и свойства инвертных точек.
Метод инверсии.
3.1.
Инверсия относительно оси ОХ.
3.2. Построение графиков y=1/f(x).
3.3. Построение графиков y= в зависимости от коэффициентов a, b, c.
4. 4.1. Инверсия относительно оси ОУ
4.2. Построение графиков у = f(1/x)
5. Применение инверсии в решении уравнений с
параметром графическим способом.
6. Список литературы.
Слайд 4 Инверсия - изменение нормального положения компонентов, расположение их в обратном
порядке. (Толковый словарь С.И. Ожегова).
Инверсия (от лат. Inversion – переворачивание,
перестановка) – термин, относящийся к перестановкам в математике.Слайд 5Цель работы:
Изучить метод инверсии и его применение при построении графиков
функций и графическом решении уравнений с параметром.
Слайд 6Задачи:
Знакомство с методом инверсии.
Рассмотрение инверсии относительно прямой, осей координат.
Изучение свойств
инверсии.
Практическое применение инверсии при построении графиков и решении уравнений.
Слайд 7Достоинства способа:
он помогает приобрести навык построения графиков функций;
он помогает усвоению
таких важных свойств функций как монотонность, экстремум, знакопостоянство, четность;
график функции
─ ее «портрет», поэтому данный способ помогает лучше увидеть свойства функции и решать уравнения с параметрами.Слайд 82. Определение и свойства инвертных точек.
Точка В называется инвертной точке
А относительно прямой (оси) е, если:
1) эти точки лежат по
одну сторону относительно е;2) отрезок, их соединяющий, перпендикулярен оси е;
3) произведение расстояний от этих точек до е равно 1 (ОА∙ОВ = 1)
4) для точек оси е инвертных нет.
Слайд 9 Преобразование плоскости, при котором каждая точка переходит в инвертную ей
относительно данной прямой, называется инверсией . Для точек этой прямой преобразование
не определяется.Слайд 103. Метод инверсии.
3.1. Инверсия относительно оси ОХ.
Рассмотрим инверсию относительно оси
ОХ.
Слайд 11 (х ; у)
(х ; ).
График функции g(x)= получается из
графика функции y=f(x) инверсией относительно оси ОХ. Слайд 12Свойства инверсии относительно оси Ох
1. Если f(x)>0, то >0.
Если f(x)
имеет корни х= х1…., т.е. f(x)=0, то g(x)= имеет вертикальные асимптоты х=х1 ….3.Если у графика функции y=f(x) есть горизонтальная асимптота у=0,то имеет асимптоту у=0.
Если у графика функции y=f(x) есть горизонтальная асимптота при , то график функции g(x)= будет иметь горизонтальную
асимптоту .
Слайд 13 4.Если f( -x)= f(x), то g(- x)=
= = g(x)
Если f(
-x)= - f(x), то g(- x)= = = -g(x).5.Если f(x) – периодическая функция, то - периодическая функция.
6. Если f(x) сохраняет знак на множестве X и возрастает на нем, то убывает на этом множестве.
Если f(x) сохраняет знак на множестве X и убывает на нем, то возрастает на этом множестве.
Слайд 14 7.Наибольшее значение функции изменяется и становится наименьшим, и наоборот. Максимум
становится минимумом, и наоборот
8. Если при x → ∞
f(x) → 0, то в графике инверсии → ∞.Если при x → ∞ f(x) → ∞, то в графике инверсии → 0.
Слайд 153.2. Построение графиков y=1/f(x).
Алгоритм построения:
1.Строим график функции y=f(x).
2.Через точки
пересечения графика функции y=f(x) с осью ОХ проводим вертикальные асимптоты или вынуть из области определения нули функции.3.Строим вспомогательные прямые у=1, у=-1.
4.Промежутки знакопостоянства сохраняем.
5.Сохраняем четность функции (симметрия графика)
6.Сохраняем периодичность функции.
7.Меняем промежутки возрастания (убывания) на промежутки убывания (возрастания).
Слайд 19График функции g(x)=f( ) получается из графика функции y=f(x)
инверсией относительно оси ОУ.
(х ; у) (
, у)
→
Слайд 20Пример 1. Построить график функции
График этой функции получается из
графика функции f(x) = инверсией относительно
оси ОУ.Слайд 21
5. Применение инверсии в решении уравнений
с параметром графическим способом.
Рассмотренная тема находит свое применение в решении
уравненийс параметрами графическим методом.
Он состоит в построении кривой, определяемой уравнением с параметром:
(а - 1)х² - 4(а - 1)х + 3а – 4 = 0
Проведем преобразования.
После преобразования получаем:
Слайд 22С помощью графика установить:
а) при каких значениях параметра а уравнение
не имеет решения;
б) при каких значениях параметра а уравнение имеет
решения разных знаков;в) при каких значениях параметра а уравнение имеет корень из отрезка [-1;2];
г) при каких значениях параметра а уравнение имеет корень больше 6.
Слайд 23Список используемой литературы
А.П. Карп «Даю уроки математики» (М., «Просвещение», 1992)
Н.Я.
Виленкин «Алгебра 9» (учебное пособие для учащихся школ и классов
с углубленным изучением математики). (М., «Просвещение», 1996)http://ru.wikipedia.org/wiki/Инверсия