Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квадратный трёхчлен Квадратные уравнения
Содержание
- 1. Квадратный трёхчлен Квадратные уравнения
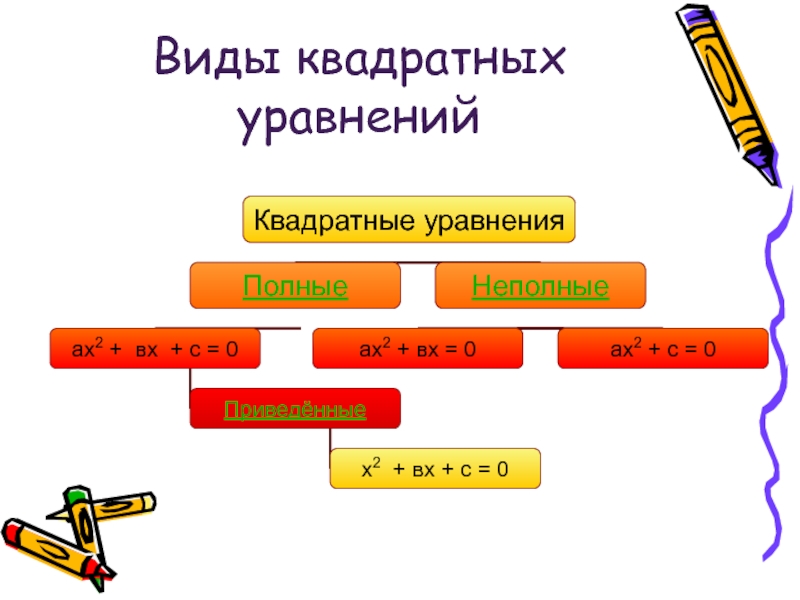
- 2. Виды квадратных уравнений
- 3. Решить эти уравнения
- 4. Квадратный трёхчлен
- 5. Значение квадратного трёхчлена Значение квадратного трёхчлена
- 6. Корни квадратного трёхчлена
- 7. Вывод Для того, чтобы
- 8. Полные квадратные уравнения ах2 +
- 9. Неполные квадратные уравнения
- 10. Приведённые квадратные уравнения
- 11. Из истории Франсуа Виет(1540-1603) французский
- 12. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 Квадратный трёхчлен
Квадратные уравнения
Определение квадратного трёхчлена
Корни квадратного трёхчлена
Учитель ГБОУ СОШ
№ 5 г. Санкт-Петербурга Очагова Неля Ивановна
Слайд 3Решить эти уравнения
х2 – 3х = 0
5х – 10х2 = 0
3х2 – 27 = 0
1/2х2 = 9
7х2 + 14 = 0
х2 + 5х + 6 = 0
х2 – 11х + 30 = 0
7х – 4х2 – 3 = 0
11х2 + 9х – 2 = 0
10х2 – 7х – 3 = 0
Слайд 4Квадратный трёхчлен
ОПРЕДЕЛЕНИЕ
Многочлен вида ах2 + вх + с, где
х переменная, а, в, с – некоторые числа, при а≠0, называется квадратным трёхчленомПримеры: 3х2 – 5х + 1
4х2 + х (4х2 + х + 0)
7х2 – 8 (7х2 – 0х – 8)
Слайд 5Значение квадратного трёхчлена
Значение квадратного трёхчлена неоднозначно, оно зависит
от значения переменной.
5х2 – 9х + 4х = 0; 5·02 - 9·0 + 4 =
= 4
х = 1; 5·12 - 9·1 + 4 =
= 0
х = 2; 5·22 - 9·2 + 4 =
= 6
х = 0,8; 5·0,82 - 9·0,8 + 4 =
= 0
Слайд 6Корни квадратного трёхчлена
Определение
Корнем квадратного трёхчлена
называется значение переменной,
при котором значение этого
трёхчлена равно 0.
Слайд 7Вывод
Для того, чтобы найти корни
квадратного трёхчлена
ах2 + вх + с,надо решить квадратное уравнение
ах2 + вх + с = 0.
Если квадратное уравнение не имеет
корней, то и квадратный трёхчлен
не имеет корней.
Слайд 8Полные квадратные уравнения
ах2 + вх + с
Д = в2 – 4ас ;
х1,2 = (-в ± √Д)/2аЕсли в – чётное число, то
Д = (в/2)2 – ас ; х1,2 = (-в/2 ± √Д)/а
Если а + в + с = 0, то х1 = 1 ; х2 = с/а
Если а – в + с = 0, то х1 = -1;х2=-с/а
Слайд 9Неполные квадратные уравнения
ах2 + вх = 0
х(ах +
в) = 0х = 0 или ах + в =0
х = -в/а
Ответ: х1=0;х2=-в/а
ах2 + с = 0
ах2 = - с
х2 = -с/а
При –с/а > 0
х1,2 = ± √-с/а
При -с/а < 0
решений нет
Слайд 10Приведённые квадратные уравнения
х2 + вх + с = 0
Удобно решать по теореме, обратнойтеореме Виета:
если х1 + х2 = -в
х1 · х2 = с ,
то х1 и х2 - корни квадратного
уравнения
Слайд 11Из истории
Франсуа Виет(1540-1603) французский математик, ввёл систему
алгебраических символов. Он был одним из первых, кто стал обозначать
числа буквами. Формулы, выражающие зависимость корнейуравнения от его коэффициентов, были
введены Виетом в 1591
году.