Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ПРИ РЕШЕНИИ ЗАДАЧ ПРИКЛАДНОГО ХАРАКТЕРА
Содержание
- 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ПРИ РЕШЕНИИ ЗАДАЧ ПРИКЛАДНОГО ХАРАКТЕРА
- 2. В математике следует помнить не формулы,
- 3. Чтобы найти на отрезке наибольшее и наименьшее
- 4. Перевести задачу на язык функций выбрать
- 5. основные этапы, при решении задач прикладного характера:формализация;решение полученной математической задачи;интерпретация найденного решения.
- 6. Буровая вышка расположена в поле в 9км
- 7. Анализ задачи:На каком расстоянии находится буровая вышка
- 8. Модель задачи в виде схематического рисунка:Р -
- 9. Постоянные величины – РА, АВ, vп, vш.Переменные
- 10. Решение задачи:1.Пусть x – расстояние АМ, 0≤x≤15;2.Из
- 11. 4. Путь S1 за время
- 12. Находим производную функции:Находим критические точки :
- 13. Слайд 13
- 14. Находим значение функции в точках:функция достигает наименьшего
- 15. Самостоятельная работа Решите задачу:Вариант 1.
- 16. Решите задачу:Вариант 2. Человек, гуляющей в лесу,
- 17. «Для меня было сложно…» 1)2)3)4)5)
- 18. Скачать презентанцию
В математике следует помнить не формулы, а процессы мышления. В. П. Ермаков ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ПРИ РЕШЕНИИ ЗАДАЧ ПРИКЛАДНОГО ХАРАКТЕРАПреподаватель: Трофименко. М.В.
Слайды и текст этой презентации
Слайд 1
«Мыслить последовательно, судить доказательно, опровергать неправильные выводы должен уметь всякий:
физик и поэт, тракторист и химик».
Слайд 2 В математике следует помнить не формулы, а процессы мышления. В.
П. Ермаков
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ПРИ РЕШЕНИИ ЗАДАЧ
ПРИКЛАДНОГО ХАРАКТЕРА
Преподаватель: Трофименко. М.В.
Слайд 3Чтобы найти на отрезке наибольшее и наименьшее значения функции, имеющей
на отрезке конечное число критических точек, нужно:
вычислить значения функции во
всех критических точках и на концах отрезка;из полученных чисел выбрать наибольшее и наименьшее.
Слайд 4Перевести задачу на язык функций
выбрать удобный параметр (х),
через который интересующую нас величину выразить как функцию f(x);
средствами
анализа найти наибольшее и наименьшее значение этой функции на некотором промежутке; выяснить, какой практический смысл (в терминах первоначальной задачи) имеет полученный (на языке функций) результат.
Слайд 5основные этапы, при решении задач прикладного характера:
формализация;
решение полученной математической задачи;
интерпретация
найденного решения.
Слайд 6 Буровая вышка расположена в поле в 9км от ближайшей точки
шоссе. С буровой надо направить курьера в пункт, расположенный по
шоссе в 15 км от упомянутой точки (считая шоссе прямолинейным). Скорость курьера на велосипеде по полю 8 км/ч, а по шоссе 10 км/ч. К какой точке шоссе ему надо ехать, чтобы в кратчайшее время достичь пункта?Задача:
Слайд 7Анализ задачи:
На каком расстоянии находится буровая вышка от ближайшей точки
шоссе?
На каком расстоянии находятся друг от друга ближайшая точка от
буровой вышки и пункт, куда надо отправить курьера?Известна ли скорость курьера на велосипеде по полю?
Известна ли скорость курьера на машине по шоссе?
Известно ли, к какой точке шоссе надо ехать, чтобы достичь нужный пункт в кратчайшее время?
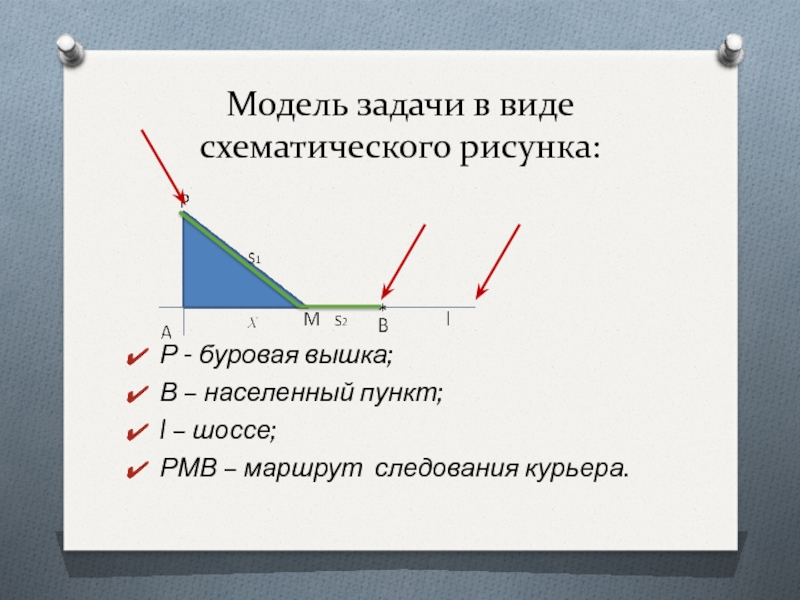
Слайд 8Модель задачи в виде схематического рисунка:
Р - буровая вышка;
В
– населенный пункт;
l – шоссе;
РМВ – маршрут следования курьера.
Слайд 9Постоянные величины – РА, АВ, vп, vш.
Переменные величины- АМ, МВ,
РМ.
Исследуемая величина – время, за которое курьеру надо доехать до
нужного пункта.РА=9км, АВ=15км. vп = 8 км/ч, vш =10 км/ч.
Слайд 10Решение задачи:
1.Пусть x – расстояние АМ, 0≤x≤15;
2.Из прямоугольного треугольника РАМ
выражаем:
3. путь S1(по полю), который курьер проходит со скоростью v
= 8 км/ч, а путь S2(по шоссе) – со скоростью v=10км/ч.
Слайд 14Находим значение функции в точках:
функция достигает наименьшего значения в точке
Ответ:
Курьеру надо ехать в точку, удаленную на 3 км от
населенного пункта и на 12 км от шоссе, чтобы в кратчайшее время достичь населенного пункта
Слайд 15
Самостоятельная работа
Решите задачу:
Вариант 1. Лодка находится на расстоянии 3
км от ближайшей точки берега А. Пассажир лодки желает достигнуть
села «В», находящегося на берегу на расстоянии 5 км от А. Лодка проплывает по 4 км/ч, а пассажир, выйдя из лодки, может в час пройти 5км. К какому пункту берега должна пристать лодка, чтобы пассажир достиг села «В» в кратчайшее время?
Слайд 16Решите задачу:
Вариант 2. Человек, гуляющей в лесу, находится в 5км
от прямолинейной дороги и в 13 км от дома, стоящего
у дороги. Скорость его передвижения в лесу 3км/ч, а по дороге 5 км/ч. Найдите наименьшее время, за которое он сможет прийти домой.
