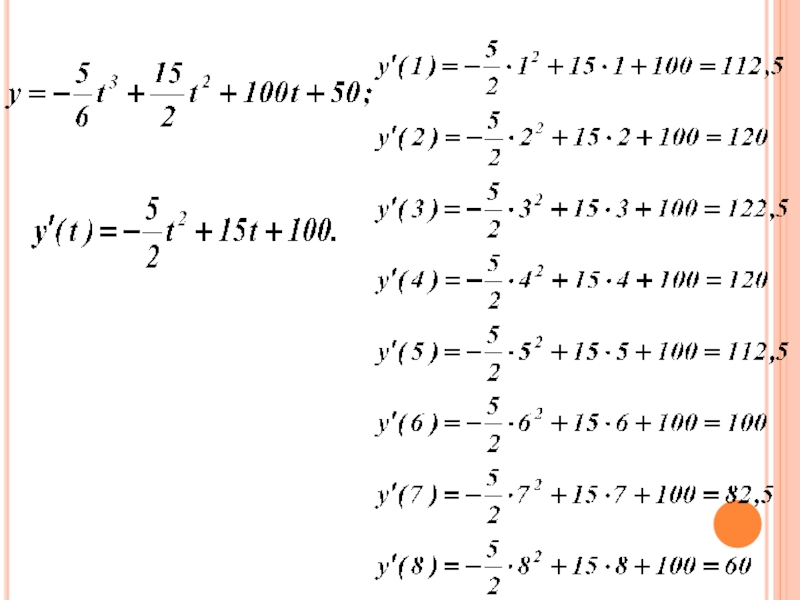Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение производной в различных областях науки
Содержание
- 1. Применение производной в различных областях науки
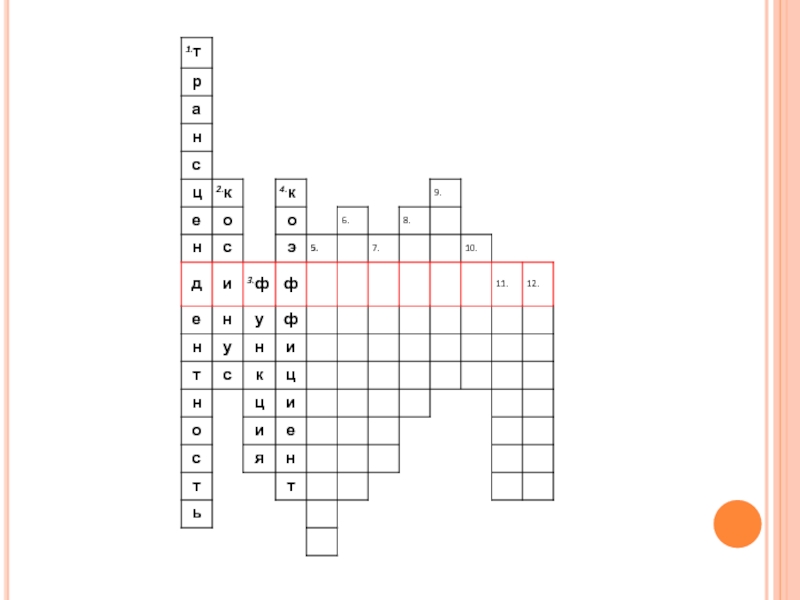
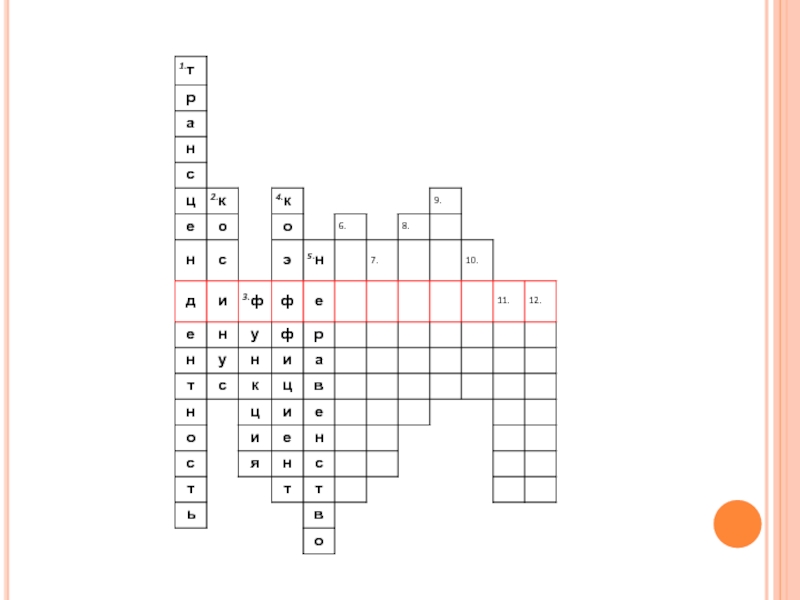
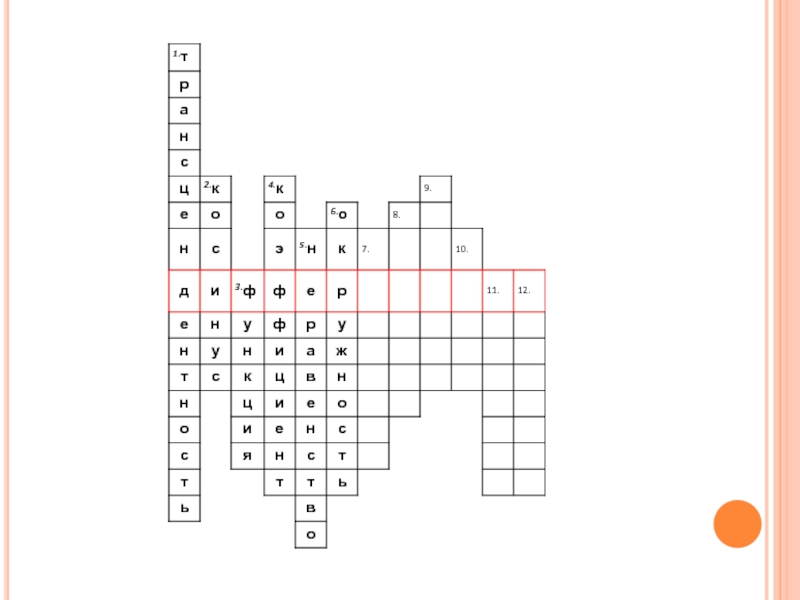
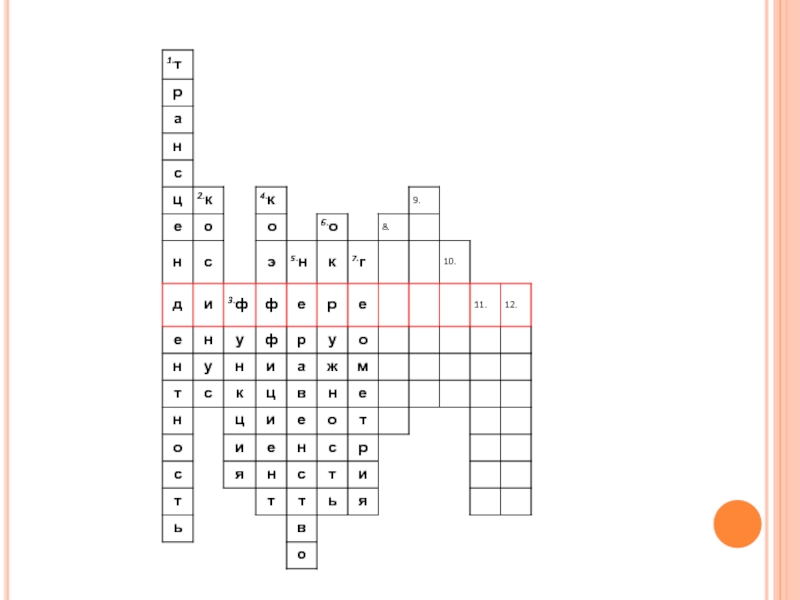
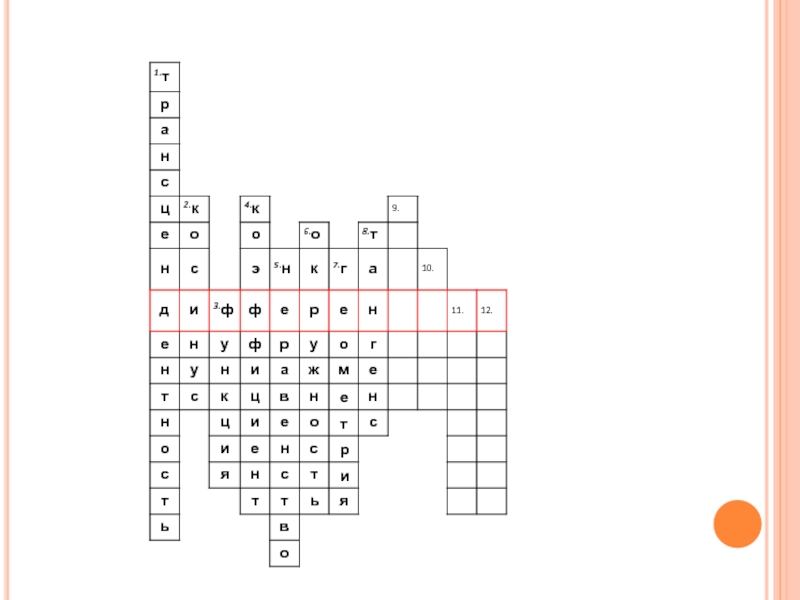
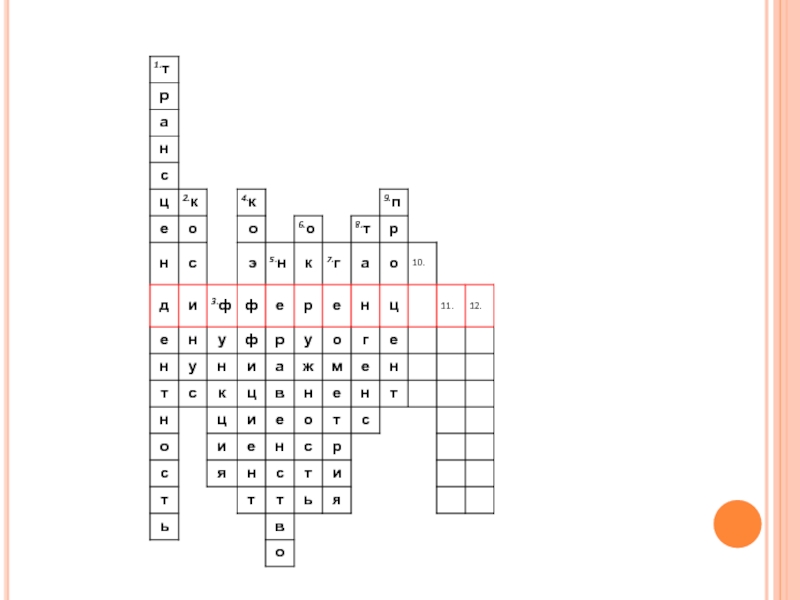
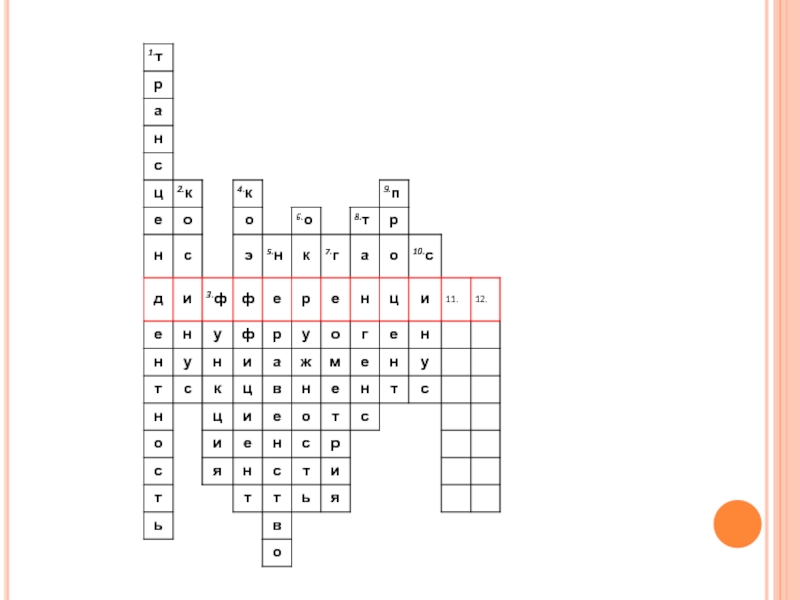
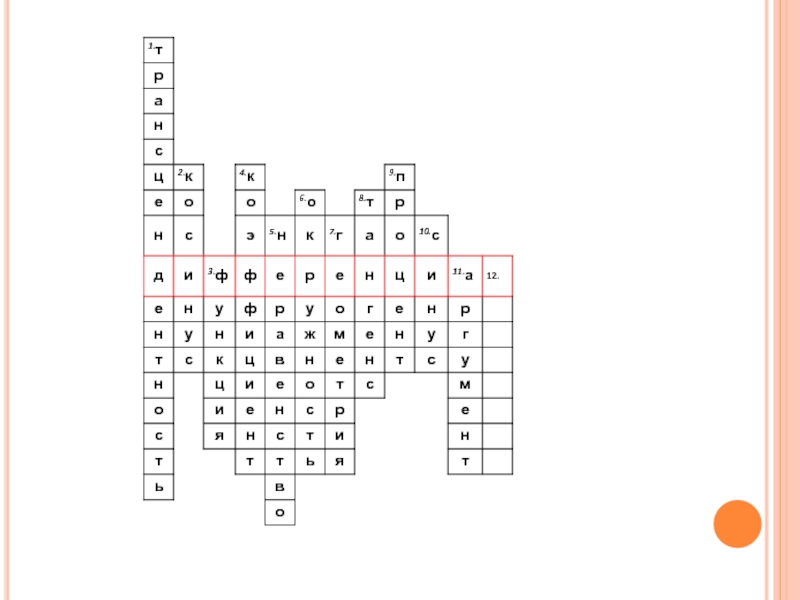
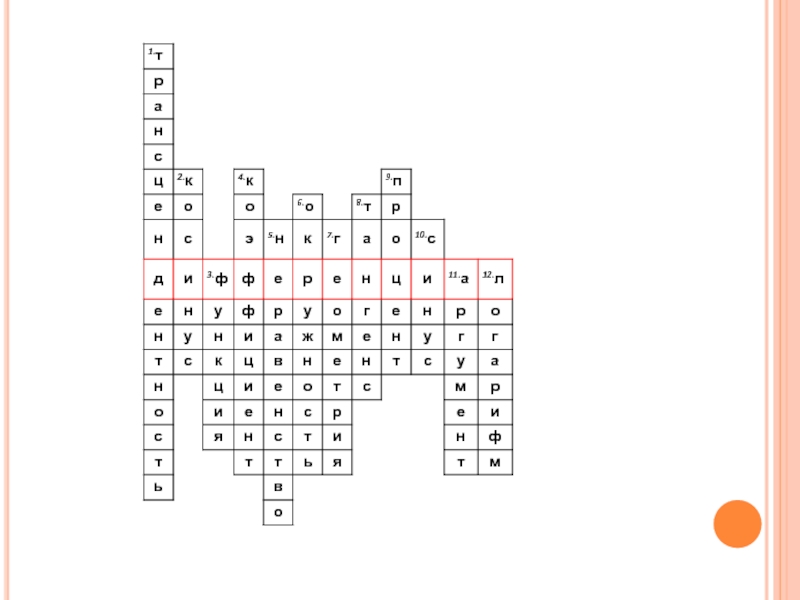
- 2. Кроссворд«Повторение-мать учения!»
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
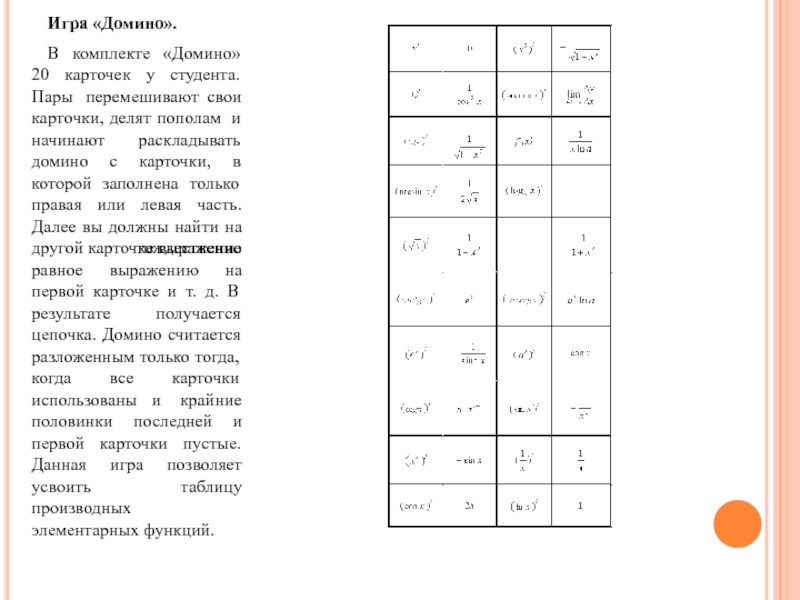
- 15. Игра «Домино». В комплекте «Домино» 20 карточек
- 16. Тема : «Применение производной в различных областях науки».
- 17. ПРОБЛЕМНЫЙ ВОПРОС Действительно ли это так?
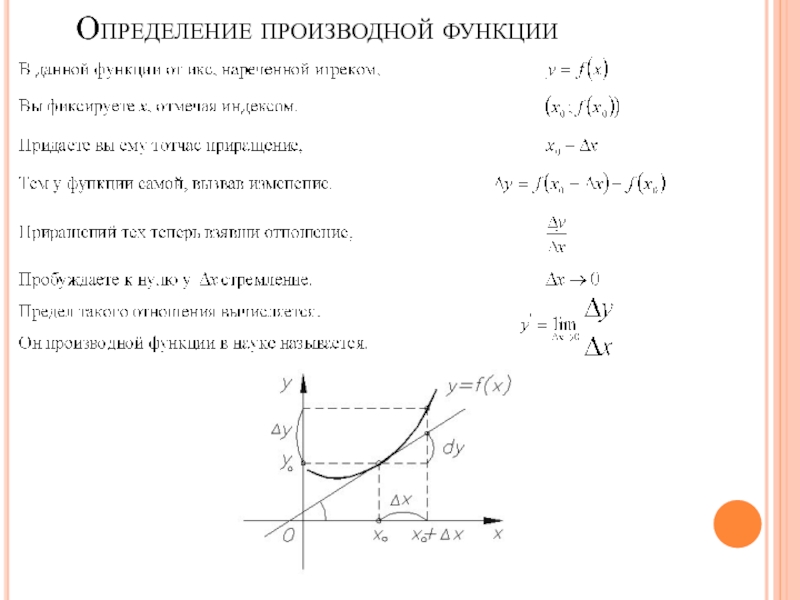
- 18. Определение производной функции
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Связь производной с биохимиейРеакция организма на введенное
- 23. Применение производной в физике Если тело
- 24. В наших домах, на транспорте, на
- 25. Задача Заряд, протекающий через проводник , меняется
- 26. Задача Расход горючего легкового автомобиля (литр
- 27. ЗадачаАвтомобиль приближается к мосту со скоростью 72
- 28. ПРОИЗВОДНАЯ В БИОЛОГИИ
- 29. v(t) = N′ (t)
- 30. Рассчитайте на основании имеющихся данных, как будет
- 31. Вспомогательные формулы и определения для решения задачиПопуляция–
- 32. Решение: По условию плотность популяции N0= 260
- 33. Относительный прирост численности популяции
- 34. Производная в химии.
- 35. Производную в химии используют для определения очень
- 36. Например, инженерам-технологам при определении эффективности
- 37. Скоростью химической реакции в химии называется
- 38. Если P(t) – закон изменения
- 39. V (t) = p ‘(t)Математическая модель производной в химии
- 40. Пусть количество вещества, вступившего в
- 41. р(t) = t2/2 + 3t –3 (моль)1.
- 42. Задача о газовой смеси Газовая смесь состоит из
- 43. Понятие производной очень важно в химии при определении скорости течения реакции.Заключение
- 44. Экономический смысл производной.
- 45. Производительность труда P(t) = v‘(t)Математическая модель производной в экономике
- 46. Объем продукции цеха в течение рабочего дня
- 47. Слайд 47
- 48. Слайд 48
- 49. Вопрос: почему после третьего часа работы мы
- 50. Вывод: Экономическое приложение производной помогает как экономистам и бизнесменам, так и обычным гражданам в распоряжении бюджетом.
- 51. ИНСТРУКЦИЯ К ПРАКТИЧЕСКОМУ ЗАНЯТИЮГруппа «Биологи-исследователи» Цель: познакомиться с
- 52. Группа «Физики-исследователи»Цель: познакомиться со cвязью производной функции
- 53. Группа «Химики-исследователи»Цель: познакомиться со связью производной функции
- 54. Группа «Экономисты-исследователи»Цель: познакомиться с особенностями исследования производственной
- 55. Задача №2Пусть функция затрат при производствеапатитового концентрата
- 56. Домашнее задание.1. Решить самостоятельно
- 57. Скачать презентанцию
Слайды и текст этой презентации
Слайд 22Связь производной с биохимией
Реакция организма на введенное лекарство может выражаться
в повышении кровяного давления, уменьшения температуры тела, изменении пульса или
других физиологических показателей. Степень реакции зависит от назначенного лекарства, его дозы. Предположим, что Х обозначает дозу назначенного лекарства, тогда У - функция степени реакции выражается формулой y = x²(a - x), где а – биомасса. При каком значении X реакция максимальна?Решение: 0< x < а. Значит y′ (x)=2ax-3x² .
Тогда
Это тот уровень дозы,
который даёт
максимальную реакцию.
Слайд 23Применение производной в физике
Если тело движется прямолинейно и
его координата изменяется по закону S(t), то скорость его движения
v(t) в момент времени t равна производной т.е. производная от координаты по времени есть скоростьПроизводная от скорости по времени есть ускорение:
Ускорение движения есть скорость изменения скорости, поэтому ускорение движения в момент времени t равно производной Таким образом, ускорение движения в момент времени t равно
т.е. равно производной от производной
Эту производную называют второй производной от функции и обозначают Итак,
Слайд 24 В наших домах, на транспорте, на заводах : всюду
работает электрический ток.
Под электрическим током понимают направленное движение свободных
электрически заряженных частиц. Количественной характеристикой электрического тока является сила тока.
В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.
=q’(t)
Слайд 25Задача
Заряд, протекающий через проводник , меняется по закону
q=sin*(2t-10)
Найти силу тока в момент времени t=5 cек.
Решение:
Найдём производную q
(q)`= cos(2t-10)2= 2cos(2t-10)
Согласно условиям задачи, t равно 5 секундам , откуда следует:
(q)`= 2cos(2*5 – 10) = 2 cos 0 = 2 (А)
Ответ: I = 2 (А).
Слайд 26Задача
Расход горючего легкового автомобиля (литр на 100 км)
в зависимости от скорости х км/ч при движении на четвертой
передаче приблизительно описывается функциейf(x)=0,0017х2-0,18х+10,2; х>30. При какой скорости расход горючего будет наименьший?
Решение:
Исследуем расход горючего с помощью производной:
f '(х)=0,0034х-0,18.
Тогда f'(х)=0 при х≈53.
Определим знак второй производной в критической точке: f''(х)=0,0034>0, следовательно, расход горючего при скорости 53 км/ч будет наименьшим. f(53)≈5,43 л.
Слайд 27Задача
Автомобиль приближается к мосту со скоростью 72 км/ч. У моста
висит дорожный знак "36км/ч". За 7 сек до въезда на
мост, водитель нажал на тормозную педаль.С разрешаемой ли скоростью автомобиль въехал на мост, если тормозной путь определяется формулой s=20t-t²?
Решение:
v(t) = s’(t) = 20 – 2t
Вычислим скорость авто,
которое оно приобретёт
через 7 секунд:
v(7) = 20- 14 = 6 (м/с)
6 м/с = 21,6 км/ч.
Ответ: Да , с разрешаемой.
Слайд 30Рассчитайте на основании имеющихся данных, как будет меняться плотность популяции
синиц через год и 2 года, если плотность синиц составляет
260 особей/га. За период размножения из одной кладки яиц в среднем выживает 3 птенца.Задача
В популяции равное число самцов и самок. Смертность синиц постоянна, в среднем за год погибает 27особей. Найти скорость роста численности популяции в год.
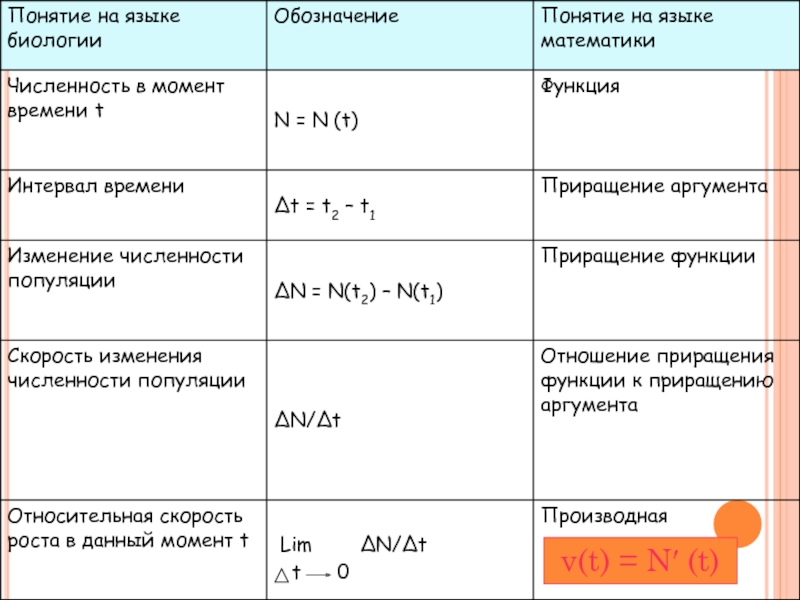
Слайд 31Вспомогательные формулы и определения для решения задачи
Популяция– это совокупность особей
данного вида, занимающих определённый участок территории внутри ареала вида, свободно
скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.Эффективная численность популяции – это совокупность особей, которые участвуют в воспроизведении потомства.(Ne)
Плотность популяции – это численность популяции на единицу площади.
Формула Ферсхюльца: N1 = (Ne - Ксмерт)( Крожд + N0 )
Скорость численности популяции : v(t)=N’(t)
Слайд 32 Решение: По условию плотность популяции N0= 260 особей/га. В популяции
равное число самцов и самок, а значит эффективная численность популяции
равна 100.Nе= 100% , тогда Nе= 1
Коэффициент смертности Ксмерт = 27% = 0,27
За год 130 пар дает 390 птенцов, т.е. (260/2)*3 =390
Формула N1 = (Nе- Ксмерт )( Крожд+ N0 ) =
= (1-0.27)(390+260)= 474 особей всего за 1-ый год N1
Слайд 33Относительный прирост численности популяции
∆N= 474/260= 1,82 раза
Тогда численность популяции будет
определяться функцией : N= 260* 1,82t где t=1,2,….Найдем тогда скорость роста численности популяции:
v(t)= N’(t) = (260*1.82t)’ = 260* (1.82t)’ =
=260*1.82t * ln 1.82 (особей/ год)
N(1) = 260*1.821= 260*1.82= 474 особи
N(2)= 260*1.822= 260*3.3124= 861 особь.
Ответ: 260*1.82t * ln 1.82 особей/ год
Слайд 35Производную в химии используют для определения очень важной вещи –
скорости химической реакции, одного из решающих факторов, который нужно учитывать
во многих областяхнаучно-производственной деятельности .
Как используют производную в химии?
Слайд 36 Например, инженерам-технологам при определении эффективности химических производств, химикам,
разрабатывающим препараты для медицины и сельского хозяйства, а также врачам
и агрономам, использующим эти препараты для лечения людей и для внесения их в почву. Одни реакции проходят практически мгновенно, другие идут очень медленно. Поэтому в реальной жизни для решения производственных задач в медицинской, сельскохозяйственной и химической промышленности просто необходимо знать скорости реакций химических веществ.Слайд 37
Скоростью химической реакции в химии называется изменение концентрации реагирующих
веществ в единицу времени или
производная от концентрации реагирующих веществ
по времени (на языке математике концентрация была бы функцией, а время – аргументом) Определение
Слайд 38 Если P(t) – закон изменения количества вещества, вступившего
в химическую реакцию, то скорость v(t) химической реакции в момент
времени t равна производной:V (t) = p ‘(t)
Формула производной в химии
Слайд 40 Пусть количество вещества, вступившего в химическую реакцию задается
зависимостью:
р(t) = t2/2 + 3t –3 (моль)
Найти скорость химической
реакции через 3 секунды.Пример задачи по химии:
Слайд 41р(t) = t2/2 + 3t –3 (моль)
1. Найдем производную функции:
Р’(t) = t +3
2. Подставим значение
t = 3 сек:P’(3) = 3 + 3 = 6 (моль/сек )
Ответ: 6 моль/сек
Решение:
Слайд 42Задача о газовой смеси
Газовая смесь состоит из окиси азота (NO)
и кислорода (O2). Требуется найти концентрацию O2 кислорода, при которой
содержащаяся в смеси окись азота окисляется с наибольшей скоростью.Решение. В условиях практической необратимости скорость реакции
2NO + O2 = 2NO2
выражается формулой v = kx2y , где x – концентрация NO в любой момент времени, y – концентрация O2 , k – константа скорости реакции, не зависит от концентрации реагирующих компонентов и зависящая только от температуры.
Концентрацию газов будем выражать в процентах. В этом случае
х + у=100.
у = 100 - х , т.к. v = kx2y, то v = kx2(100-х) = k(100x2 - x3)= v (x) при x[0; 100]
x=0 или 200-3x=0
-3x=-200
x= -200: (-3)
x= 66.67 % [0; 100]
v ’ (10) > 0, v ’ (100) < 0. Следовательно скорость наибольшая , когда
х ≈ 66,67%, и у =100-x= 33,33%.
Ответ: m(NO)≈ 66,67% и m(O2) ≈ 33,33%.
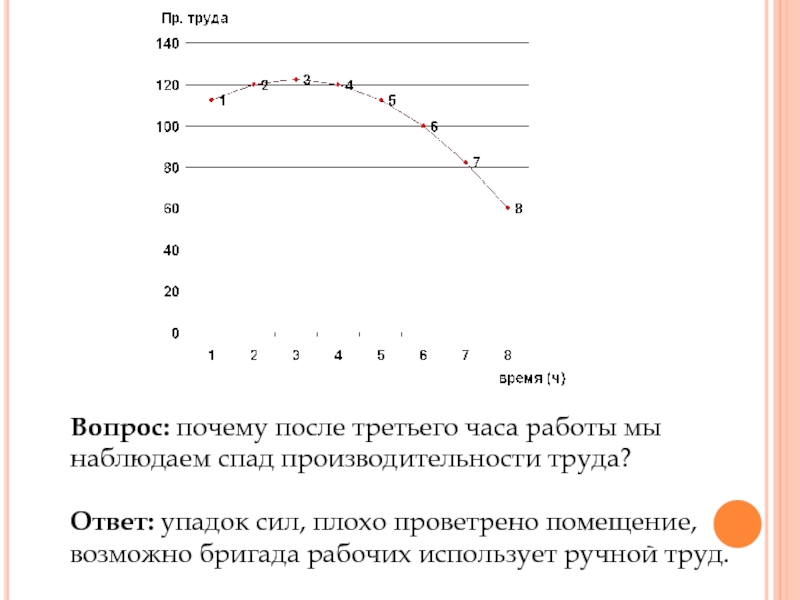
Слайд 46Объем продукции цеха в течение рабочего дня представляет функцию –
рабочее время в часах. Вычислить максимальную производительность труда в течение
рабочего дня.Слайд 49Вопрос: почему после третьего часа работы мы наблюдаем спад производительности
труда?
Ответ: упадок сил, плохо проветрено помещение, возможно бригада рабочих использует
ручной труд.Слайд 50Вывод: Экономическое приложение производной помогает как экономистам и бизнесменам, так
и обычным гражданам в распоряжении бюджетом.
Слайд 51ИНСТРУКЦИЯ К ПРАКТИЧЕСКОМУ ЗАНЯТИЮ
Группа «Биологи-исследователи»
Цель: познакомиться с особенностями исследования численности
популяции, его спада или роста, и выявления причин того или
иного процесса; для этого выполнить задания, записать ход решения, сделать выводы.Ход работы:
Задание №1.
В среду вносят популяцию из 1000 бактерий. Численность (p) популяции
возрастает по закону p(t)= 1000 + , где t выражается в часах.
Найти максимальный размер этой популяции и проанализировать
результат.
Задание №2.
Рассчитайте на основании имеющихся данных, как будет меняться
плотность популяции мушек дрозофил через год и 2 года, если
плотность популяции составляет 256000 особей/га. За период
размножения из одной кладки яиц в среднем выживает 22 особи. В
популяции равное число самцов и самок. Смертность дрозофил постоянна,
в среднем за год погибает 36% особей. Найти скорость роста численности
популяции в год. Полученные данные проанализировать.
Слайд 52Группа «Физики-исследователи»
Цель: познакомиться со cвязью производной функции в физике,
определить насколько это важно для задач практического характера; для
этого выполнить задания, записать ход решения, сделать выводы.Ход работы:
Задание №1.
Заряд, протекающий через проводник, меняется по
закону q=sin3 (2t-10). Найти силу тока в момент t=50 сек.
Задание №2.
Тело массой m0 движется прямолинейно по закону
s(t)= αt2 +βt+ γ, где α, β, γ – постоянные. Доказать, что
сила, действующая на тело, постоянна .
Слайд 53Группа «Химики-исследователи»
Цель: познакомиться со связью производной функции с химией; для
этого выполнить задания, записать ход решения, сделать выводы.
Ход работы:
Задание
№1. Смесь состоит из серы(S) и кислорода(O2). Требуется найти
концентрацию кислорода(O2), при которой сера(S) реагирует с
наибольшей скоростью.
Задание №2.
При какой концентрации азота(N2) и водорода(H2) реакция будет
достигать наивысшей скорости, если в результате их
взаимодействия образуется аммиак(NH3).
Слайд 54Группа «Экономисты-исследователи»
Цель: познакомиться с особенностями исследования производственной функции , её
спада или роста, и выявления причин того или иного процесса;
для этого выполнить задания, записать ход решения, сделать выводы.Ход работы:
Задача №1
Цементный завод производит X тонн цемента в день. По договору он
должен ежедневно поставлять строительной фирме не менее 20 тонн
цемента. Производственные мощности завода таковы, что выпуск не
может превышать 90 тонн в день.
Определить:
1) при каком объёме производства удельные затраты производства будут наибольшими ( наименьшими);
2) выгодно ли строительной фирме быть единственным партнёром завода?
Функция суммарных затрат имеет вид: K(x)= - x3 + 98x2 + 200x
Слайд 55Задача №2
Пусть функция затрат при производстве
апатитового концентрата имеет вид:
К(Х)=
Определить предельные
издержки
производства при увеличении объёма
выпуска на x=2 единицы и на
x=10 единиц.
Вопрос:
выгодно ли данномупредприятию наращивать
производство, если уровень затрат не
изменится?
Слайд 56 Домашнее задание.
1. Решить самостоятельно задачи.
а) Смесь состоит из углерода (С) и алюминия (Al). Требуется найти концентрацию углерода (С), при которой содержащаяся в смеси карбида алюминия реагирует с наибольшей скоростью. б) Первоначальная численность популяции состоит из 3000 особей. Найти максимальный размер этой популяции, если ее численность р(t) возрастает по закону
, где t выражается в часах.
2. Шкиль Н. И. и др. Математика: алгебра и начала математического анализа (базовый и углублённый уровень). 10-11 кл.- К.: Зодиак-ЭКО, 2014.
§15, п. 15.1-15.3