Центральная и осевая симметрия

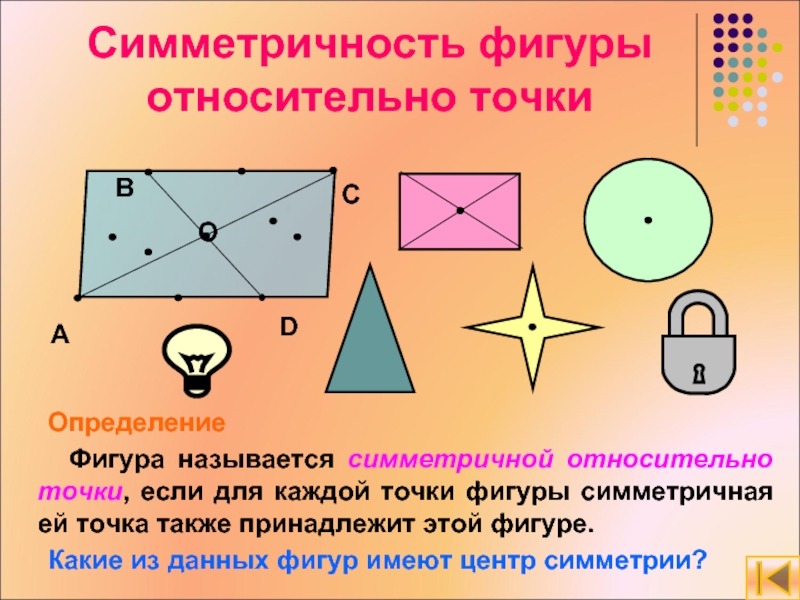
фигуры относительно точки
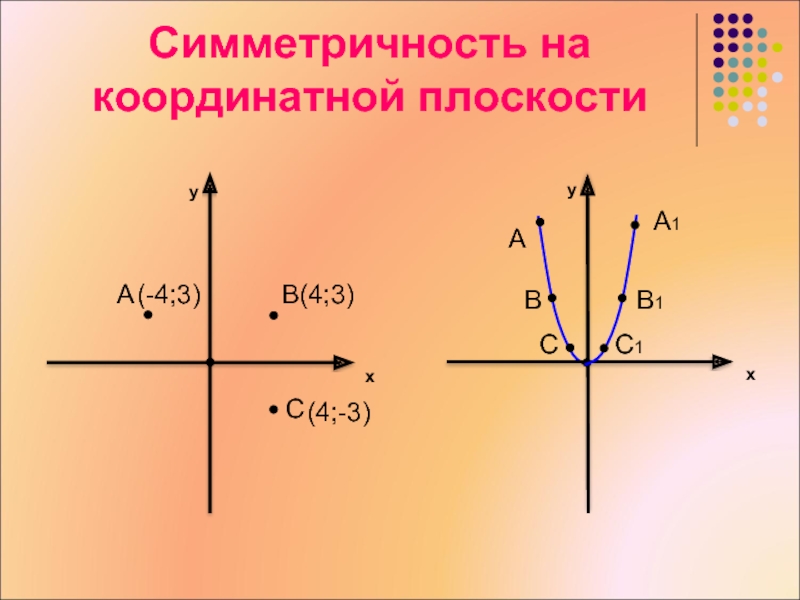
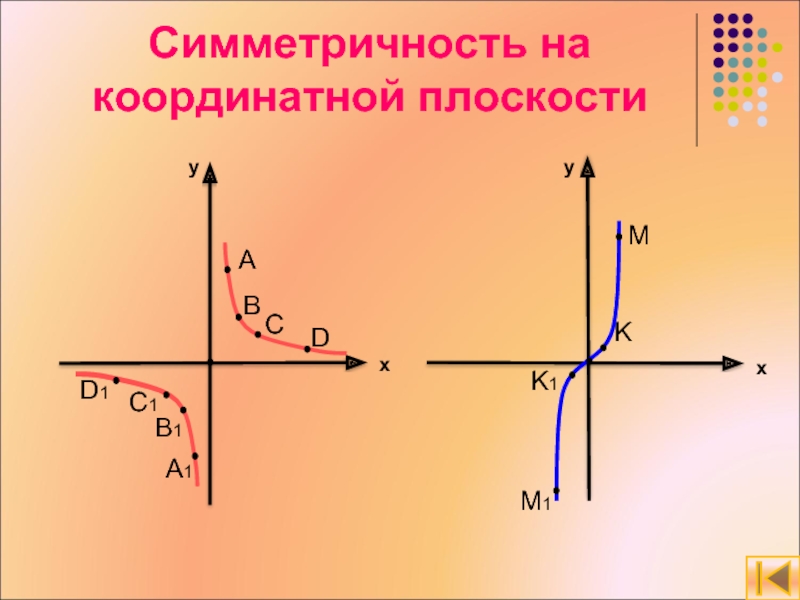
Симметрия на координатной плоскости
Симметрия вокруг нас
Математики о симметрии
Проверим

знания
Задания

Содержание

А1 называются симметричными относительно прямой а, если эта прямая проходит

через середину отрезка АА1 и перпендикулярна к нему

A1

A

a

O

B

A A1

a

Т

AO = OA1

если для каждой точки фигуры симметричная ей точка также принадлежит

этой фигуре

А

D

B

C

M

K

N

P

a

b

c

симметричными относительно точки О, если О – середина отрезка AA1


Задание

Постройте отрезок A1B1, симметричный отрезку AB относительно точки О

A

O

A

B

B1

O

A1

A1

точки, если для каждой точки фигуры симметричная ей точка также

принадлежит этой фигуре.
Какие из данных фигур имеют центр симметрии?

A

B

C

D

O

Максвелл Д.

Красота

тесно связана с симметрией
Вейль Г.

Симметрия … является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство
Вейль Г.

Для человеческого разума симметрия обладает, по - видимому, совершенно особой притягательной силой
Фейнман Р.